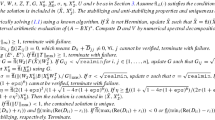Skip to main content
SpringerLink
Log in

Robust verification algorithm for stabilizing solutions of discrete-time algebraic Riccati equations

  • Original Paper
  • Published:
Japan Journal of Industrial and Applied Mathematics Aims and scope Submit manuscript

Abstract

A robust algorithm is proposed for numerically computing an interval matrix containing the stabilizing solution of a discrete-time algebraic Riccati equation. This algorithm is based on estimating an upper bound for the spectral radius of a matrix power utilizing the Perron–Frobenius theory. The algorithm moreover verifies the uniqueness of the contained solution. Numerical results show that the algorithm is more successful than the previous algorithms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. Although the accuracy of \(\tilde{X}\) is unknown at this stage, it is enough to show \(\rho (A_{\tilde{X}}) < 1\).

References

  1. Abels, J., Benner, P.: DAREX - A collection of benchmark examples for discrete-time algebraic Riccati equations. SLICOT Working Note 1999–2016 (1999). http://slicot.org/objects/software/reports/SLWN1999-16.ps.gz

  2. Bini, D.A., Iannazzo, B., Meini, B.: Numerical Solution of Algebraic Riccati Equations. SIAM Publications, Philadelphia (2012)

    MATH  Google Scholar 

  3. Bouhamidi, A., Heyouni, M., Jbilou, K.: Block Arnoldi-based methods for large scale discrete-time algebraic Riccati equations. J. Comput. Appl. Math. 236, 1531–1542 (2011)

    Article  MathSciNet  Google Scholar 

  4. Frobenius, G.: Über Matrizen aus positiven Elementen, 1. Sitzungsber. Königl. Preuss. Akad. Wiss. pp. 471–476 (1908)

  5. Frobenius, G.: Über Matrizen aus positiven Elementen, 2. Sitzungsber. Königl. Preuss. Akad. Wiss. pp. 514–518 (1909)

  6. Higham, N.J.: Functions of Matrices: Theory and Computation. SIAM Publications, Philadelphia (2008)

    Book  Google Scholar 

  7. Luther, W., Otten, W.: Verified calculation of the solution of algebraic Riccati equation. In: Csendes, T. (ed.) Developments in Reliable Computing, pp. 105–118. Kluwer Academic Publishers, Dordrecht (1999)

    Chapter  Google Scholar 

  8. Luther, W., Otten, W., Traczinski, H.: Verified calculation of the solution of continuous- and discrete time algebraic Riccati equation. Schriftenreihe des Fachbereichs Mathematik der Gerhard–Mercator–Universit\(\ddot{\text{a}}\)t Duisburg, Duisburg, SM-DU-422 (1998)

  9. Lancaster, P., Rodman, L.: Algebraic Riccati Equations. Clarendon Press, Oxford (1995)

    MATH  Google Scholar 

  10. Miyajima, S.: Fast verified computation for stabilizing solutions of discrete-time algebraic Riccati equations. J. Comput. Appl. Math. 319, 352–364 (2017)

    Article  MathSciNet  Google Scholar 

  11. Miyajima, S.: Verified computation for the Hermitian positive definite solution of the conjugate discrete-time algebraic Riccati equation. J. Comput. Appl. Math. 350, 80–86 (2019)

    Article  MathSciNet  Google Scholar 

  12. Rump, S.M.: INTLAB - INTerval LABoratory. In: Csendes, T. (ed.) Developments in Reliable Computing, pp. 77–107. Kluwer Academic Publishers, Dordrecht (1999)

    Chapter  Google Scholar 

  13. Zhou, B., Lam, J., Duan, G.-R.: Toward solution of matrix equation \(X = Af (X)B + C\). Linear Algebra Appl. 435, 1370–1398 (2011)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The author acknowledges the reviewer for valuable comments.

Author information

Authors and Affiliations

  1. Faculty of Science and Engineering, Iwate University, 4-3-5 Ueda, Morioka-shi, Iwate, 020-8551, Japan

    Shinya Miyajima

Authors
  1. Shinya Miyajima
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shinya Miyajima.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work was partially supported by JSPS KAKENHI Grant Number JP16K05270.

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Miyajima, S. Robust verification algorithm for stabilizing solutions of discrete-time algebraic Riccati equations. Japan J. Indust. Appl. Math. 36, 763–776 (2019). https://doi.org/10.1007/s13160-019-00353-7

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13160-019-00353-7

Keywords

Mathematics Subject Classification

Search

Navigation