The Design of Intervention Trials Involving Recurrent and Terminal Events

Abstract

Clinical trials are often designed to assess the effect of therapeutic interventions on the incidence of recurrent events in the presence of a dependent terminal event such as death. Statistical methods based on multistate analysis have considerable appeal in this setting since they can incorporate changes in risk with each event occurrence, a dependence between the recurrent event and the terminal event, and event-dependent censoring. To date, however, there has been limited development of statistical methods for the design of trials involving recurrent and terminal events. Based on the asymptotic distribution of regression coefficients from a multiplicative intensity Markov regression model, we derive sample size formulas to address power requirements for both the recurrent and terminal event processes. We consider the design of trials for which separate marginal hypothesis tests are of interest for the recurrent and terminal event processes and deal with both superiority and non-inferiority tests. Simulation studies confirm that the designs satisfy the nominal power requirements in both settings, and an application to a trial evaluating the effect of a bisphosphonate on skeletal complications is given for illustration.

Appendix

1.1 Asymptotic Equivalence of the Partial Score Statistics

Under the null hypothesis, $m^{-\frac{1}{2}}$ times the partial score statistic (6) can be written as

Using similar arguments in the proofs of Theorems 4.2.1 and 4.3.1 of Gill [35], one can show that the second term of the above expression converges in probability to zero as m→∞ for every β ₀.

Similarly, let

be the associated martingale process for the recurrent event under the alternative hypothesis. One can write the partial score statistic (6) under the alternative hypothesis as follows:

(27)

Using similar arguments as for the null hypothesis, one can show the second term converges in probability to zero as m→∞ for every β ₀. We now show the last term of the above expression converges in probability to zero as m→∞. From the regularity conditions of Andersen and Gill [23], the integrand is locally bounded for every u∈(0,τ]. Note that the last term can be written as

(28)

where $R_{j}^{(a)}(\beta_{0}, u)$ converges almost surely to $E_{A}(R_{j}^{(a)}(\beta_{0}, u))$ at each time point u, a=0,1. It follows from the Slutsky’s theorem that the first term of the integrand in (28) converges almost surely to zero as m→∞ at every u. By the central limit theorem,

(29)

converges in distribution to a normal random variable at every u with mean μ as dΛ _0j (u)P(τ _i >u) times

$$\sum_{v=0}^1 P\bigl(Z_{i}(u)=j|Z_{i}(0)=0, v_i=v\bigr )P(v_i=k)e^{\beta_Av} $$

and the variance

Then, for every u the integrand in (28) converges in probability to zero. Therefore, it follows from the Lebesgue’s dominated convergence theorem that (28) converges in probability to zero as m→∞.

A similar approached can be used to prove the asymptotic equivalence of the partial score statistics (7) is (14) under the null hypothesis and (16) under the alternative hypothesis.

1.2 Evaluation of Expectations Under the True Model

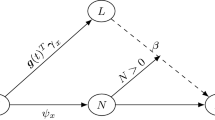
The necessary expectations require the evaluation of the probability being in state j at time t, P(Z _i (t)=j|Z _i (0)=0), for the proposed Markov process in Fig. 1. As an example, the calculation of $E_{0}(\bar{Y}_{ij}(u)e^{\beta_{0} v_{i}} d\varLambda_{0j}(u) )$ in (10), is carried out as follows:

The transition probabilities are computed as described in the following section.

1.3 Evaluation of the Transition Probability Matrix

The evaluation of expectations under particular models requires the calculation of the Markov transition probability matrix; for notational convenience we suppress the dependence on i. We consider a finite state space with J+1 states corresponding to the cumulative number of recurrent events from 0 to J and one absorbing state D for the terminal event. For 0≤s≤t, let P(s,t|v) be the (J+2)×(J+2) transition probability matrix with (k,ℓ) entry

(30)

for ℓ=k+1 or D, k=0,1,…,J. Let Q ^v(t) denote the transition intensity matrix for individuals in treatment group v, the elements of which are based on the intensities λ _k (t|H(t)) and γ _k (t|H(t)) defined in Sect. 2.

For a time-homogeneous process adopted at the design stage, let λ _k (t|H(t))=λ _k and γ _k (t|H(t))=γ _k be the intensities for k−1→k and k−1→D transitions, respectively. The transition intensity matrix can then be written simply as Q ^v. and has (k,ℓ) entry given by λ _k for k=1,…,J and ℓ=k+1, γ _k for k=1,…,J and ℓ=J+2, −(λ _k +γ _k ) for k=ℓ=1,…,J, and zero otherwise. Under such a time-homogeneous Markov model, P(s,s+t)=P(0,t)=P(t) and P(t)=exp(Q ^v t).

There are several approaches available to compute P(t) for a given transition intensity matrix Q ^v. If Q ^v has J+2 linearly independent eigenvectors, let A be a matrix of eigenvectors, and note that AQ ^v A ⁻¹ is a diagonal matrix with the eigenvalues d ₁,d ₂,…,d _J+2 of Q ^v along its diagonal. Then by the spectral value decomposition [34],

$$\exp\bigl(Q^v t\bigr)=A \operatorname{diag} \bigl(e^{d_1t}, \ldots, e^{d_{J+2}t}\bigr)A^{-1} . $$

If Q ^v does not have J+2 linearly independent eigenvectors, the Jordan canonical form can be used instead [36]. For some nonsingular matrix B, the Jordan canonical form of Q ^v is $BQ^{v}B^{-1}=\mathcal{J}=\operatorname{diag}(\mathcal{J}_{1}(d_{1}), \mathcal{J}_{2}(d_{2}), \ldots, \mathcal{J}_{p}(d_{p}) )$ and

(31)

is a n _k ×n _k matrix and n ₁+n ₂+⋯+n _p =J+2. The matrix exponential exp(Q ^v t) can be computed [37] as

and in this case $f(\mathcal{J}_{k}(d_{k}))$ takes the form

Numerically, the Jordan decomposition can be obtained through the MATLAB function jordan for a given Q ^v and the construction of (31) and hence the transition probability matrix P(t) can be easily computed in MATLAB. Other methods for computing matrix exponentials are reviewed in Moler and Van Loan [38]. Another numerically stable approach is the method of scaling and squaring [39], which has been employed by MATLAB function expm based on an optimal approach [40]. We used this function in sample size calculations for the trial design in cancer metastatic to bone in Sect. 6.

Supplementary Materials

The software for sample size calculations using the proposed method is available from the first author upon request.