Skip to main content
SpringerLink
Log in

Real-time repairable interpolation scheme for CNC tool path processing

  • Published:
International Journal of Precision Engineering and Manufacturing Aims and scope Submit manuscript

Abstract

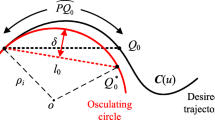
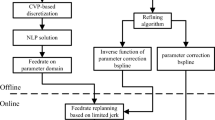
G01 trajectory is widely-adopted for CNC machining. The piecewise linear trajectory is geometrically discontinuous, bringing about drastic fluctuation of feedrate and acceleration, and causing low machining efficiency and quality. Many methods of trajectory smoothing are developed and applied in CNC system. However some shortcomings exist when these methods were applied in CNC machining. In the existing methods, the following requirements are not satisfied simultaneously: not less than G2 continuity, confined chord error, shape preservation, interpolating G01 points, spatial applicability, real-time performance of algorithm, free geometric form. Considering various requirements of CNC machining, this work develops an interpolation scheme with local repairing function to deal with the possible shape deficiencies of trajectory. The resulting tool path has G2 continuity and is optimized in bending energy under shape-preserving and chord error constraints. Combining with jerk-limited feedrate scheduling, a real-time tool path processing strategy is developed. The simulation demonstrates the proposed method eliminates shape deficiencies, and has apparent advantage in the reduction of contour error, curvature, bending energy and machining time, compared with Zhao’s and Fan’s methods. The experiment demonstrates the advantages of the proposed algorithm in improving the quality of machined surface and machining efficiency, compared with previous methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Schumaker, L. I., “On Shape Preserving Quadratic Spline Interpolation,” SIAM Journal on Numerical Analysis, Vol. 20, No. 4, pp. 854–864, 1983.

    Article  MathSciNet  MATH  Google Scholar 

  2. De Boor, C., Höllig, K., and Sabin, M., “High Accuracy Geometric Hermite Interpolation,” Computer Aided Geometric Design, Vol. 4, No. 4, pp. 269–278, 1987.

    Article  MathSciNet  MATH  Google Scholar 

  3. Ferguson, J. C. and Pruess, S., “Shape-Preserving Interpolation by Parametric Piecewise Cubic Polynomials,” Computer-Aided Design, Vol. 23, No. 7, pp. 498–505, 1991.

    Article  MATH  Google Scholar 

  4. Degen, W. L. F., “High Accurate Rational Approximation of Parametric Curves,” Computer Aided Geometric Design, Vol. 10, No. 3, pp. 293–313, 1993.

    Article  MathSciNet  MATH  Google Scholar 

  5. Sakai, M., “Osculatory Interpolation,” Computer Aided Geometric Design, Vol. 18, No. 8, pp. 739–750, 2001.

    Article  MathSciNet  MATH  Google Scholar 

  6. Koninckx, B. and Van Brussel, H., “Real-Time Nurbs Interpolator for Distributed Motion Control,” CIRP Annals-Manufacturing Technology, Vol. 51, No. 1, pp. 315–318, 2002.

    Article  Google Scholar 

  7. Yong, J.-H. and Cheng, F. F., “Geometric Hermite Curves with Minimum Strain Energy,” Computer Aided Geometric Design, Vol. 21, No. 3, pp. 281–301, 2004.

    Article  MathSciNet  MATH  Google Scholar 

  8. Popiel, T. and Noakes, L., “Bézier Curves and C2 Interpolation in Riemannian Manifolds,” Journal of Approximation Theory, Vol. 148, No. 2, pp. 111–127, 2007.

    Article  MathSciNet  MATH  Google Scholar 

  9. Yau, H.-T. and Wang, J.-B., “Fast Bezier Interpolator with Real-Time Lookahead Function for High-Accuracy Machining,” International Journal of Machine Tools and Manufacture, Vol. 47, No. 10, pp. 1518–1529, 2007.

    Article  Google Scholar 

  10. Farin, G., “Geometric Hermite Interpolation with Circular Precision,” Computer-Aided Design, Vol. 40, No. 4, pp. 476–479, 2008.

    Article  Google Scholar 

  11. Wang, J.-B. and Yau, H.-T., “Real-Time NURBS Interpolator: Application to Short Linear Segments,” The International Journal of Advanced Manufacturing Technology, Vol. 41, No. 11-12, pp. 1169–1185, 2009.

    Article  Google Scholar 

  12. Walton, D. J. and Meek, D. S., “G2 Hermite Interpolation with Circular Precision,” Computer-Aided Design, Vol. 42, No. 9, pp. 749–758, 2010.

    Article  MATH  Google Scholar 

  13. Jaklic, G., Kozak, J., Krajnc, M., Vitrih, V., and Žagar, E., “On Interpolation by Planar Cubic,” Mathematics of Computation, Vol. 79, No. 269, pp. 305–326, 2010.

    Article  MathSciNet  MATH  Google Scholar 

  14. Jaklic, G. and Žagar, E., “Planar Cubic G1 Interpolatory Splines with Small Strain Energy,” Journal of Computational and Applied Mathematics, Vol. 235, No. 8, pp. 2758–2765, 2011.

    Article  MathSciNet  MATH  Google Scholar 

  15. Jaklic, G. and Žagar, E., “Curvature Variation Minimizing Cubic Hermite Interpolants,” Applied Mathematics and Computation, Vol. 218, No. 7, pp. 3918–3924, 2011.

    Article  MathSciNet  MATH  Google Scholar 

  16. Krajnc, M., “Interpolation Scheme for Planar Cubic G2 Spline Curves,” Acta Applicandae Mathematicae, Vol. 113, No. 2, pp. 129–143, 2011.

    Article  MathSciNet  MATH  Google Scholar 

  17. Albrecht, G. and Romani, L., “Convexity Preserving Interpolatory Subdivision with Conic Precision,” Applied Mathematics and Computation, Vol. 219, No. 8, pp. 4049–4066, 2012.

    Article  MathSciNet  MATH  Google Scholar 

  18. Abbas, M., Majid, A. A., and Ali, J. M., “Monotonicity-Preserving C2 Rational Cubic Spline for Monotone Data,” Applied Mathematics and Computation, Vol. 219, No. 6, pp. 2885–2895, 2012.

    Article  MathSciNet  MATH  Google Scholar 

  19. Li, Y. and Deng, C., “C-Shaped G2 Hermite Interpolation with Circular Precision based on Cubic PH Curve Interpolation,” Computer-Aided Design, Vol. 44, No. 11, pp. 1056–1061, 2012.

    Article  MathSciNet  Google Scholar 

  20. Farouki, R. T., Manni, C., Sampoli, M. L., and Sestini, A., “Shape-Preserving Interpolation of Spatial Data by Pythagorean-Hodograph Quintic Spline Curves,” IMA Journal of Numercial Analysis, Vol. 35, No. 1, pp. 478–498, 2015.

    Article  MathSciNet  MATH  Google Scholar 

  21. Bajaj, C. L. and Xu, G., “A-Splines: Local Interpolation and Approximation using Gk-Continuous Piecewise Real Algebraic Curves,” Computer Aided Geometric Design, Vol. 16, No. 6, pp. 557–578, 1999.

    Article  MathSciNet  MATH  Google Scholar 

  22. Piazzi, A., Romano, M., and Bianco, C. G. L., “G3-Splines for the Path Planning of Wheeled Mobile Robots,” Proc. of European Control Conference (ECC), pp. 1845–1850, 2003.

    Google Scholar 

  23. Renka, R. J., “Shape-Preserving Interpolation by Fair Discrete G3 Space Curves,” Computer Aided Geometric Design, Vol. 22, No. 8, pp. 793–809, 2005.

    Article  MathSciNet  MATH  Google Scholar 

  24. Fan, W., Lee, C.-H., and Chen, J.-H., “A Realtime Curvature-Smooth Interpolation Scheme and Motion Planning for CNC Machining of Short Line Segments,” International Journal of Machine Tools and Manufacture, Vol. 96, pp. 27–46, 2015.

    Article  Google Scholar 

  25. Fan, W., Lee, C. H., Chen, J. H., and Xiao, Y., “Real-Time Bezier Interpolation Satisfying Chord Error Constraint for CNC Tool Path,” Science China Technological Sciences, Vol. 59, No. 2, pp. 203–213, 2016.

    Article  Google Scholar 

  26. Zhang, K., Guo, J.-X., and Gao, X.-S., “Cubic Spline Trajectory Generation with Axis Jerk and Tracking Error Constraints,” Int. J. Precis. Eng. Manuf., Vol. 14, No. 7, pp. 1141–1146, 2013.

    Article  Google Scholar 

  27. Yuen, A., Zhang, K., and Altintas, Y., “Smooth Trajectory Generation for Five-Axis Machine Tools,” International Journal of Machine Tools and Manufacture, Vol. 71, pp. 11–19, 2013.

    Article  Google Scholar 

  28. Walton, D. J. and Meek, D. S., “G2 Blends of Linear Segments with Cubics and Pythagorean-Hodograph Quintics,” International Journal of Computer Mathematics, Vol. 86, No. 9, pp. 1498–1511, 2009.

    Article  MathSciNet  MATH  Google Scholar 

  29. Zhang, M., Yan, W., Yuan, C., Wang, D., and Gao, X., “Curve Fitting and Optimal Interpolation on CNC Machines based on Quadratic BSplines,” Science China Information Sciences, Vol. 54, No. 7, pp. 1407–1418, 2011.

    Article  MathSciNet  MATH  Google Scholar 

  30. Zhang, L. B., You, Y. P., He, J., and Yang, X. F., “The Transition Algorithm based on Parametric Spline Curve for High-Speed Machining of Continuous Short Line Segments,” The International Journal of Advanced Manufacturing Technology, Vol. 52, No. 1-4, pp. 245–254, 2011.

    Article  Google Scholar 

  31. Yan, C. Y., Lee, C. H., and Yang, J. Z., “Three-Axis Tool-Path BSpline Fitting based on Preprocessing, Least Square Approximation and Energy Minimization and Its Quality Evaluation,” Modern Machinery (MM) Science Journal, DOI No. 10.17973/MMSJ.2012_ 11_201219, 2012.

    Google Scholar 

  32. Zhao, H., Zhu, L. M., and Ding, H., “A Real-Time Look-Ahead Interpolation Methodology with Curvature-Continuous B-Spline Transition Scheme for CNC Machining of Short Line Segments,” International Journal of Machine Tools and Manufacture, Vol. 65, pp. 88–98, 2013.

    Article  Google Scholar 

  33. Ahmad, A. and Ali, J. M., “G3 Transition Curve between Two Straight Lines,” Proc. of 5th International Conference on Computer Graphics, Imaging and Visualisation, pp. 154–159, 2008.

    Google Scholar 

  34. Fang, L., “G3 Approximation of Conic Sections by Quintic Polynomial Curves,” Computer Aided Geometric Design, Vol. 16, No. 8, pp. 755–766, 1999.

    Article  MathSciNet  MATH  Google Scholar 

  35. Lu, L., “An Explicit Method for G3 Merging of Two Bézier Curves,” Journal of Computational and Applied Mathematics, Vol. 260, pp. 421–433, 2014.

    Article  MathSciNet  MATH  Google Scholar 

  36. Hartmann, E., “Parametric Gn Blending of Curves and Surfaces,” The Visual Computer, Vol. 17, No. 1, pp. 1–13, 2001.

    Article  MATH  Google Scholar 

  37. Beudaert, X., Lavernhe, S., and Tournier, C., “5-Axis Local Corner Rounding of Linear Tool Path Discontinuities,” International Journal of Machine Tools and Manufacture, Vol. 73, pp. 9–16, 2013.

    Article  Google Scholar 

  38. Tulsyan, S. and Altintas, Y., “Local Toolpath Smoothing for Five-Axis Machine Tools,” International Journal of Machine Tools and Manufacture, Vol. 96, pp. 15–26, 2015.

    Article  Google Scholar 

  39. Shi, J., Bi, Q., Zhu, L., and Wang, Y., “Corner Rounding of Linear Five-Axis Tool Path by Dual PH Curves Blending,” International Journal of Machine Tools and Manufacture, Vol. 88, pp. 223–236, 2015.

    Article  Google Scholar 

  40. Farouki, R. T., “The Elastic Bending Energy of Pythagorean-Hodograph Curves,” Computer Aided Geometric Design, Vol. 13, No. 3, pp. 227–241, 1996.

    Article  MathSciNet  MATH  Google Scholar 

  41. Shiller, Z. and Lu, H.-H., “Robust Computation of Path Constrained Time Optimal Motions,” Proc. of IEEE International Conference on Robotics and Automation, pp. 144–149, 1990.

    Chapter  Google Scholar 

  42. Timar, S. D., Farouki, R. T., Smith, T. S., and Boyadjieff, C. L., “Algorithms for Time-Optimal Control of CNC Machines Along Curved Tool Paths,” Robotics and Computer-Integrated Manufacturing, Vol. 21, No. 1, pp. 37–53, 2005.

    Article  Google Scholar 

  43. Yuan, C., Zhang, K., and Fan, W., “Time-Optimal Interpolation for CNC Machining Along Curved Tool Pathes with Confined Chord Error,” Journal of Systems Science and Complexity, Vol. 26, No. 5, pp. 836–870, 2013.

    Article  MathSciNet  MATH  Google Scholar 

  44. Dong, J., Ferreira, P., and Stori, J., “Feed-Rate Optimization with Jerk Constraints for Generating Minimum-Time Trajectories,” International Journal of Machine Tools and Manufacture, Vol. 47, No. 12, pp. 1941–1955, 2007.

    Article  Google Scholar 

  45. Fan, W., Gao, X.-S., Lee, C.-H., Zhang, K., and Zhang, Q., “Time-Optimal Interpolation for Five-Axis CNC Machining along Parametric Tool Path based on Linear Programming,” The International Journal of Advanced Manufacturing Technology, Vol. 69, No. 5-8, pp. 1373–1388, 2013.

    Article  Google Scholar 

  46. Fan, W., Gao, X.-S., Yan, W., and Yuan, C.-M., “Interpolation of Parametric CNC Machining Path Under Confined Jounce,” The International Journal of Advanced Manufacturing Technology, Vol. 62, No. 5-8, pp. 719–739, 2012.

    Article  Google Scholar 

  47. Tseng, S. J., Lin, K. Y., Lai, J. Y., and Ueng, W. D., “A Nurbs Curve Interpolator with Jerk-Limited Trajectory Planning,” Journal of the Chinese Institute of Engineers, Vol. 32, No. 2, pp. 215–228, 2009.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Mechanical Manufacturing Technology, China Academy of Engineering Physics, Mianyang, 621999, China

    Wei Fan

  2. National NC System Engineering Research Center, Huazhong University of Science and Technology, Wuhan, 430074, China

    Wei Fan, Chen-Han Lee & Ji-Hong Chen

Authors
  1. Wei Fan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chen-Han Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ji-Hong Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wei Fan.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fan, W., Lee, CH. & Chen, JH. Real-time repairable interpolation scheme for CNC tool path processing. Int. J. Precis. Eng. Manuf. 17, 1673–1684 (2016). https://doi.org/10.1007/s12541-016-0194-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12541-016-0194-6

Keywords

Search

Navigation