Skip to main content
SpringerLink
Log in

Investigation on the stability of periodic motions of a flexible rotor-bearing system with two unbalanced disks

  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

Abstract

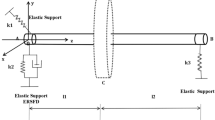
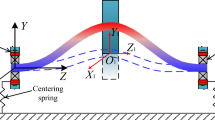
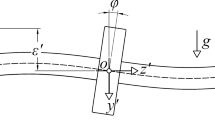
The stability of periodic motion of a rotor-bearing system with two unbalanced disks is analyzed based on a multi-degree of freedom (M-DOF) finite element model. Nonlinear effects of supporting oil-film and inertia distributions as well as shearing effect are taken into account. Focusing on the more realistic FE method to study the stability of nonlinear rotor-bearing system with the influence of the eccentricity phase, the stability calculation of the M-DOF FE model is done by using the combination of Shooting method and Newmark method. Experiments with a rotor-bearing test rig (two disks on a shaft with two bearings) are then performed and results are presented. It is found that typical instability characteristic is successfully produced. Through comparisons between calculated results and measurements, it is shown that the combination of Shooting method and Newmark method in studying the M-DOF rotor-bearing system is useful, especially for the complex rotor-bearing system. In addition, altering eccentricity phase of the two disks can significantly influence instability type and speed. When the two disks are out of phase, the occurring of oil whip is restrained effectively. It is suggested that a careful examination should be made in modeling more complex non-linear rotor-bearing system. Some response curves are shown to compare the beam motions at different load velocities.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. F. F. Ehrich, Some observations of chaotic vibration phenomena in high-speed rotor dynamics, Journal of Vibration and Acoustics, 113 (1) (1991) 50–57.

    Article  Google Scholar 

  2. Y. B. Kim and S. T. Noah, Quasi-periodic response and stability analysis for a non-linear Jeffcott rotor, Journal of Sound and Vibration, 190 (2) (1996) 239–253.

    Article  Google Scholar 

  3. G. Adiletta, A. R. Guido and C. Rossi, Chaotic motions of a rigid rotor in short journal bearings, Nonlinear Dynamics, 10 (3) (1996) 251–269.

    Article  Google Scholar 

  4. G. Adiletta, A. R. Guido and C. Rossi, Nonlinear dynamics of a rigid unbalanced rotor in journal bearings. Part I: Theoretical Analysis, Nonlinear Dynamics, 14 (1) (1997) 57–87.

    Article  MATH  Google Scholar 

  5. G. Adiletta, A. R. Guido and C. Rossi, Nonlinear dynamics of a rigid unbalanced rotor in journal bearings. Part II: Experimental Analysis, Nonlinear Dynamics, 14 (2) (1997) 157–198.

    Article  Google Scholar 

  6. A. Muszynska, Improvements in lightly loaded rotor/bearing and rotor/seal models, Journal of Vibration Acoustics-Transactions of the ASME, 110 (2) (1988) 129–136.

    Article  Google Scholar 

  7. A. Muszynska and D. E. Bently, Anti-swirl arrangements prevent rotor/seal instability, Journal of Vibration Acoustics-Transactions of the ASME, 111 (2) (1989) 156–162.

    Article  Google Scholar 

  8. A. Muszynska and D. E. Bently, Frequency-swept rotating input perturbation techniques and identification of the ?uid force models in rotor/bearing/seal systems and fluid handling machines, Journal of Sound and Vibration, 143 (1) (1990) 103–124.

    Article  Google Scholar 

  9. C. Wang, C. Lo and C. Chen, Nonlinear dynamic analysis of a flexible rotor supported by externally pressurized porous gas journal bearings, ASME Journal of Tribology, 124 (3) (2002) 553–561.

    Article  Google Scholar 

  10. C. L. Chen and H. T. Yau, Chaos in the imbalance response of a flexible rotor supported by oil film bearings with nonlinear suspension, Nonlinear Dynamics, 16 (1) (1998) 71–90.

    Article  MATH  MathSciNet  Google Scholar 

  11. K. Gjika, L. S. Andres and G. D. Larue, Nonlinear dynamic behavior of turbocharger rotor-bearing systems with hydrodynamic oil film and squeeze film damper in series: prediction and experiment, Journal of Computational and Nonlinear Dynamics, 5 (4) (2010) 1–8.

    Article  Google Scholar 

  12. C. W. Chang-Jian and C. K. Chen, Chaos and bifurcation of a flexible rub-impact rotor supported by oil film bearings with nonlinear suspension, Mechanism and Machine Theory, 42 (3) (2007) 312–333.

    Article  MATH  Google Scholar 

  13. J. Ding, Computation of multi-plane imbalance for a multibearing rotor system, Journal of Sound and Vibration, 205 (3) (1997) 364–371.

    Article  Google Scholar 

  14. G. Meng and R. Gasch, Stability and stability degree of a cracked flexible rotor supported on journal bearings, ASME Journal of Vibration and Acoustics, 122 (2) (2000) 116–125.

    Article  Google Scholar 

  15. R. Brancati, E. Rocca and M. Russo, Journal orbits and their stability for rigid unbalanced rotors, ASME Journal of Tribology, 117 (4) (1995) 709–716.

    Article  Google Scholar 

  16. Y. S. Chen and Q. Meng, Bifurcations of a nonlinear rotorbearing system, Journal of Vibration Engineering, 9 (3) (1996) 266–275.

    MATH  MathSciNet  Google Scholar 

  17. S. Chen, Q. Ding and Q. Meng, Analysis of the instability of low frequency vibration of rotor system, Journal of Applied Mechanics, 15 (1) (1998) 113–117.

    Google Scholar 

  18. Y. C. Pei, Stability boundaries of a spinning rotor with parametrically excited gyroscopic system, European Journal of Mechanics, 28 (4) (2009) 891–896.

    Article  MATH  Google Scholar 

  19. F. Chu and Y. Tang, Stability and nonlinear responses of a rotor-bearing system with pedestal looseness, Journal of Sound and Vibration, 241 (5) (2001) 879–893.

    Article  Google Scholar 

  20. J. Y. Zhao and E. J. Huhn, Subharmonic, quasi-periodic and chaotic motions of a rigid rotor supported by an eccentric squeeze film damper, Journal of Mechanical Engineering Science, 207 (6) (1993) 383–392.

    Article  Google Scholar 

  21. J. Y. Zhao, I. W. Linnett and L. J. Mclean, Subharmonic and quasi-periodic motions of an eccentric squeeze film damper-mounted rigid rotor, Journal of Vibration and Acoustics, 116 (3) (1994) 357–363.

    Article  Google Scholar 

  22. Q. Ding, J. E. Cooper and A. Y. T. Leung, Hopf bifurcation analysis of a rotor/seal system, Journal of Sound and Vibration, 252 (5) (2002) 817–833.

    Article  Google Scholar 

  23. Q. Ding and A. Y. T. Leung, Numerical and experimental investigations on flexible multi-bearing rotor dynamics, Journal of Vibration and Acoustics, 127 (4) (2005) 408–415.

    Article  Google Scholar 

  24. N. Zhang, N. J. Wu and Z. S. Liu, Simulation research on oil whirl fault in a high-speed rotor-bearing system, International Journal of Plant Engineering and Management, 15 (2) (2010) 65–72.

    MathSciNet  Google Scholar 

  25. W. H. Xie, Y. G. Tang and Y. S. Chen, Analysis of motion stability of the flexible rotor-bearing system with two unbalanced disks, Journal of Sound and Vibration, 310 (1) (2008) 381–393.

    Google Scholar 

  26. T. Zheng and N. Hasebe, An efficient analysis of highorder dynamical system with local nonlinearity, Journal of Vibration and Acoustics, 121 (3) (1999) 408–416.

    Article  Google Scholar 

  27. T. Zheng and N. Hasebe, Nonlinear dynamic behaviors of a complex rotor-bearing system, Journal of Applied Mechanics, 67 (3) (2000) 485–495.

    Article  MATH  Google Scholar 

  28. J. Jing, G. Meng, Y. Sun and S. Xia, On the oil-whipping of a rotor-bearing system by a continuum model, Applied Mathematical Modelling, 29 (5) (2005) 461–475.

    Article  MATH  Google Scholar 

  29. J. Jing, G. Meng, Y. Sun and S. Xia, On the non-linear dynamic behavior of a rotor-bearing system, Journal of Sound and Vibration, 274 (3) (2004) 1031–1044.

    Article  Google Scholar 

  30. Y. Cui, Z. Liu, S. Leng, W. Han and W. Huang, Study on nonlinear stability for a 200 MW turbo-generator rotorbearing system, Chinese Journal of Mechanical Engineering, 41 (2) (2005) 170–175.

    Article  Google Scholar 

  31. K. J. Bathe, Finite element procedures, Prentic-Hall, Englewood Cliffs (1999).

    Google Scholar 

  32. Q. S. Lu, Qualitative methods and divergent of ordinary differential equation, Beijing: Beijing University of aeronautics and Astronautics press (1989).

    Google Scholar 

  33. J. M. T. Thompson and B. Stewart, Nonlinear dynamic and chaos, John Wiley, New York (1986).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mechanical Engineering & Automation, Northeastern University, Shenyang, 110819, China

    Chaofeng Li, Shihua Zhou, Hexing Yu & Bangchun Wen

  2. Mechanical & Mining Engineering, University of Queensland, Brisbane, St Lucia, QLD, 4072, Australia

    Shijie Jiang

Authors
  1. Chaofeng Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shihua Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shijie Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hexing Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Bangchun Wen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chaofeng Li.

Additional information

Recommended by Associate Editor Ohseop Song

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, C., Zhou, S., Jiang, S. et al. Investigation on the stability of periodic motions of a flexible rotor-bearing system with two unbalanced disks. J Mech Sci Technol 28, 2561–2579 (2014). https://doi.org/10.1007/s12206-014-0613-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-014-0613-5

Keywords

Search

Navigation