Games with a permission structure - A survey on generalizations and applications

Abstract

In the field of cooperative games with restricted cooperation, various restrictions on coalition formation are studied. The most studied restrictions are those that arise from restricted communication and hierarchies. This survey discusses several models of hierarchy restrictions and their relation with communication restrictions. In the literature, there are results on game properties, Harsanyi dividends, core stability, and various solutions that generalize existing solutions for TU-games. In this survey, we mainly focus on axiomatizations of the Shapley value in different models of games with a hierarchically structured player set, and their applications. Not only do these axiomatizations provide insight in the Shapley value for these models, but also by considering the types of axioms that characterize the Shapley value, we learn more about different network structures. A central model of games with hierarchies is that of games with a permission structure where players in a cooperative transferable utility game are part of a permission structure in the sense that there are players that need permission from other players before they are allowed to cooperate. This permission structure is represented by a directed graph. Generalizations of this model are, for example, games on antimatroids, and games with a local permission structure. Besides discussing these generalizations, we briefly discuss some applications, in particular auction games and hierarchically structured firms.

1 Introduction

A situation in which a finite set of players can generate certain payoffs by cooperation can be described by a cooperative game with transferable utility (or simply a TU-game). A TU-game consists of a player set, and for every subset of the player set, called a coalition, a real number which is the worth that the coalition of players can earn when they agree to cooperate.

In a TU-game, there are no restrictions on the cooperation possibilities of the players, i.e. every coalition is feasible and can generate a worth. Various models with restrictions on coalition formation are discussed in the literature. The most applied restrictions are those arising from restrictions in communication and hierarchies. In this survey, we discuss several models where cooperation is restricted because the players are part of some hierarchical structure. We review several of such models and their relations. Considering payoff allocation we focus on the Shapley value, but other solutions such as the nucleolus, Banzhaf value or Core are considered in the literature.

A central model in this is that of games with a permission structure which describe situations in which the players in a TU-game are part of a hierarchical organization that is represented by a directed graph, referred to as a permission structure, such that there are players that need permission from other players before they are allowed to cooperate. Various assumptions can be made about how a permission structure affects the cooperation possibilities. In the conjunctive approach, it is assumed that every player needs permission from all its predecessors before it is allowed to cooperate. Alternatively, in the disjunctive approach, it is assumed that every player needs permission from at least one of its predecessors before it is allowed to cooperate with other players.¹

To take account of the limited cooperation possibilities, for every game with a permission structure a modified game is defined which assigns to every coalition the worth of its largest feasible subcoalition in the original game. The disjunctive and conjunctive approach yield different modified games. A solution for games with a permission structure is a function that assigns to every such a game a payoff distribution over the individual players. Applying solutions for TU-games to the modified games yields solutions for games with a permission structure. Applying the Shapley value to the two restricted games described above yields two different solutions for games with a permission structure: the conjunctive and the disjunctive (Shapley) permission values.

Games with a permission structure can be generalized in various ways, for example to games on antimatroids. Antimatroids are combinatorial structures which, besides permission structures, also generalize other models such as ordered partition voting where players are partitioned into levels, and a coalition in a certain level can be active only if a majority of players in higher levels approve. Since antimatroids are union closed (i.e. the union of any two feasible coalitions is also feasible), a similar approach as for games with a permission structure can be followed by defining a restricted game that assigns to every coalition the worth of its largest feasible subset in the original game, and applying the Shapley value (or any other TU-game solution) to this restricted game. We discuss how some results can be generalized to this framework. After that we argue that antimatroids are a natural counterpart for undirected communication graphs in the sense that they are defined by properties that are similar to properties that characterize connected coalitions in undirected communication graphs.

A special class of games with a permission structure that has many applications in economics and operations research is the class of peer group games which are also a special case of so-called digraph games. Peer group games are derived from peer group situations being games with a permission structure where the game is additive and the permission structure is a rooted tree. Applications are, e.g. polluted river games, liability games, the duals of airport games, auction games and ATM games. Digraph games are directly defined for weighted digraphs (with weights on the nodes/players) and are applied to measure domination or centrality in directed networks. A model that generalizes games with a permission structure as well as digraph games are games with a local permission structure where players need permission from their predecessors to cooperate, but do not need permission from their predecessors to allow their successors to cooperate. In this sense, authority and value generation are separated.

From the many applications of games with a permission structure, we will briefly discuss two: (i) auction games which are an application of peer group games, and (ii) hierarchically structured firms where the permission structure is a rooted tree and the game is convex such that the only nonnull players are those at the lowest level of the hierarchy, i.e. those players that have no successors (the other players are supposed to be managers who coordinate the production process but do not produce value themselves).

This survey is organized as follows. In Sect. 2, we discuss the central model of games with a permission structure. In Sect. 3, we generalize permission structures to antimatroids. In Sect. 4, we compare hierarchies with communication graphs, and argue that antimatroids are a natural counterpart for communication graphs. In Sect. 5, we discuss games with a local permission structure that generalize games with a permission structure as well as digraph games. In Sect. 6, we discuss some applications. We end with some concluding remarks in Sect. 7.

2 Games with a permission structure

2.1 Cooperative TU-games

A situation in which a finite set of players $N \subset {\mathbb {N}}$ can generate certain payoffs by cooperation can be described by a cooperative game with transferable utility (or simply a TU-game), being a pair (N, v) where $v :2^N \rightarrow {\mathbb {R}}$ is a characteristic function on N satisfying $v(\emptyset ) = 0$. For every coalition $E \subseteq N$, $v(E) \in {\mathbb {R}}$ is the worth of coalition E, i.e. the members of coalition E can obtain a total payoff of v(E) by agreeing to cooperate. Since we take the player set to be fixed, we denote a TU-game (N, v) just by its characteristic function v and refer to this simply as a game. We denote the collection of all TU-games (characteristic functions) on player set N by ${\mathcal {G}}^N$.

A payoff vector for game $v \in {\mathcal {G}}^N$ is an |N|-dimensional vector $x \in {\mathbb {R}}^N$ assigning a payoff $x_i \in {\mathbb {R}}$ to any player $i \in N$. A (single-valued) solution for TU-games is a function f that assigns a payoff vector $f(v) \in {\mathbb {R}}^N$ to every TU-game $v \in {\mathcal {G}}^N$. One of the most famous solutions for TU-games is the Shapley value (Shapley 1953) given by

$$\begin{aligned} Sh_i(v) = \frac{1}{|N|!}\sum _{\pi \in \varPi (N)} m^\pi _i(v), \end{aligned}$$

where $\varPi (N)$ is the set of all permutations of N, and for every permutation $\pi :N \rightarrow N$, the corresponding marginal vector $m^\pi (v)$ is given by $m^\pi _i(v)=v(\{j \in N \mid \pi (j) \le \pi (i)\}) - v(\{j \in N \mid \pi (j) < \pi (i)\})$ for all $i \in N$.

The Core (Gillies 1953) of $v \in {\mathcal {G}}^{N}$ is the set of all efficient payoff vectors that are group stable in the sense that no coalition can do better by separating, and is given by

$$\begin{aligned} \hbox {Core}(v)=\left\{ x\in {\mathbb {R}}^N \left| \sum _{i\in N}x_i=v(N) {\text { and }} \sum _{i\in E}x_{i}\ge v(E)\quad {\text {for all }} E\subset N\right. \right\} . \end{aligned}$$

As known, the Core of a game is nonempty if and only if the game is balanced, see, e.g. Bondareva (1963) or Shapley (1967).

Next, we recall some game properties. Game $v \in {\mathcal {G}}^N$ is monotone if $v(E) \le v(F)$ for all $E \subseteq F \subseteq N$. We denote the class of all monotone TU-games on N by ${\mathcal {G}}^N_M$. Game $v \in {\mathcal {G}}^N$ is superadditive if $v(E \cup F) \ge v(E) + v(F)$ for all $E, F \subseteq N$ such that $E \cap F = \emptyset$. Game $v \in {\mathcal {G}}^N$ is convex if $v(E \cup F) + v(E \cap F) \ge v(E) + v(F)$ for all $E, F \subseteq N$. Note that every convex game is superadditive. A game is additive or inessential if $v(E)=\sum _{i \in E} v(\{i\})$ for all $E \subseteq N$.

For two games $v, w \in {\mathcal {G}}^N$, the game $(v + w) \in {\mathcal {G}}^N$ is given by $(v + w)(E) = v(E) + w(E)$ for all $E \subseteq N$.

For every $T\subseteq N$, $T \ne \emptyset$, the unanimity game $u_T$ is given by $u_T(E)=1$ if $T\subseteq E$, and $u_T(E)=0$ otherwise. It is well known that the unanimity games form a basis for ${\mathcal {G}}^N$: for every $v \in {\mathcal {G}}^N$ it holds that $v = \sum _{\mathop {T \ne \emptyset }\limits ^{T \subseteq N}} \varDelta _v(T)u_T$, where $\varDelta _v(T) = \sum _{E \subseteq T} (-1)^{|T|-|E|} v(E)$ are the Harsanyi dividends, see Harsanyi (1959). Using these Harsanyi dividends, the Shapley value also can be written as:

$$\begin{aligned} Sh_i(v)=\sum _{\mathop {i \in E}\limits ^{E \subseteq N}} \frac{\varDelta _v(E)}{|E|}\quad {\text {for all }} i \in N. \end{aligned}$$

2.2 Games with a permission structure

A game with a permission structure describes a situation where some players in a TU-game need permission from other players before they are allowed to cooperate with other players in a coalition. Formally, a permission structure is a directed graph on N. A directed graph or digraph is a pair (N, D) where $N=\{1,...,n\}$ is a finite set of nodes (representing the players) and $D\subseteq N\times N$ is a binary relation on N. We assume the digraph to be irreflexive, i.e., $(i,i) \not \in D$ for all $i \in N$. Since we take the player set to be fixed, we simply refer to D for a digraph, and we denote the collection of all irreflexive digraphs on N by ${\mathcal {D}}^N$. For $i\in N$, the nodes in $S_D(i):=\{j\in N\mid (i,j)\in D\}$ are called the successors of i, and the nodes in $P_D(i):=\{j\in N\mid (j,i)\in D\}$ are called the predecessors of i in D. For given $D \in {\mathcal {D}}^N$, a (directed) path from i to j in N is a sequence of distinct nodes $(h_{1},\ldots ,h_{t})$ such that $h_{1}=i,$ $h_{k+1} \in S_D(h_k)$ for $k=1,\ldots ,t-1$, and $h_{t}=j$. The transitive closure of $D \in {\mathcal {D}}^N$ is the digraph tr(D) given by $(i,j) \in tr(D)$ if and only if there is a directed path from i to j. By $\widehat{S}_D(i)=S_{tr(D)}(i)$, we denote the set of successors of i in the transitive closure of D, and refer to these players as the subordinates of i in D. We refer to the players in $\widehat{P}_D(i) = \{j \in N \mid i \in \widehat{S}_D(j)\}$ as the superiors of i in D. A digraph $D\in {\mathcal {D}}^N$ is transitive if $D=tr(D)$. For a set of players $E \subseteq N$, we denote by $S_D(E) = \bigcup _{i \in E} S_D(i)$, respectively, $P_D(E) = \bigcup _{i \in E} P_D(i)$, the sets of successors, respectively predecessors of players in coalition E. Also, for $E \subseteq N$, we denote $\widehat{S}_D(E) = \cup _{i \in E}~\widehat{S}_D(i)$ and $\widehat{P}_D(E) = \cup _{i \in E}~\widehat{P}_D(i)$.

A directed path $(i_{1},\ldots ,i_{t})$, $t \ge 2$, in D is a cycle in D if $(i_t,i_1) \in D$. We call digraph D acyclic if it does not contain any cycle. Note that acyclicity of digraph D implies that D has at least one node that does not have a predecessor. We refer to these as top nodes, and denote the set of top nodes by $TOP(D) = \{i \in N \mid P_D(i) = \emptyset \}$. A permission structure D on N is quasi-strongly connected if there exists an $i_0 \in N$ such that $\widehat{S}_D(i_0) = N \setminus \{i_0\}$. A permission structure D on N is hierarchical if it is acyclic and quasi-strongly connected. We denote the collection of all hierarchical permission structures on N by ${\mathcal {D}}^N_H$.

A triple (N, v, D) with $N \subset {\mathbb {N}}$ a finite set of players, $v \in {\mathcal {G}}^N$ a TU-game and $D \in {\mathcal {D}}^N$ a digraph on N is called a game with a permission structure. Again, since we take the player set N to be fixed, we denote a game with a permission structure just as a pair (v, D). In the conjunctive approach as introduced in Gilles et al. (1992) and van den Brink and Gilles (1996), it is assumed that a player needs permission from all its predecessors to cooperate with other players. Therefore, a coalition is feasible if and only if for every player in the coalition all its predecessors are also in the coalition. So, for permission structure D the set of conjunctive feasible coalitions is given by

$$\begin{aligned} \varPhi ^c_D = \left\{ E \subseteq N \left| P_D(i) \subseteq E \quad {\text {for all }} i \in E \right. \right\} . \end{aligned}$$

For every $E \subseteq N$, let $\sigma ^c_D(E) = \bigcup _{\{F \in \varPhi ^c_D \mid F \subseteq E\}} F = E \setminus \widehat{S}_D(N \setminus E)$ be the largest conjunctive feasible subset² of E in the collection $\varPhi ^c_D$. Then, the induced conjunctive restricted game of the pair (v, D) is the game $r_{v,D}^c :2^{N}\rightarrow {\mathbb {R}}$ that assigns to every coalition $E \subseteq N$ the worth of its largest conjunctive feasible subset, i.e.

$$\begin{aligned} r_{v,D}^c (E) = v(\sigma ^c_D(E)) \quad {\text {for all }} E \subseteq N. \end{aligned}$$

(1)

A solution for games with a permission structure is a function f that assigns a payoff distribution $f(v,D) \in {\mathbb {R}}^N$ to every game with permission structure (v, D) on N. The conjunctive (Shapley) permission value $\varphi ^c$ is the solution that assigns to every game with a permission structure the Shapley value of the conjunctive restricted game, thus

$$\begin{aligned} \varphi ^c(v,D) = Sh(r_{v,D}^c)\quad {\text {for all }} (v,D) \in {\mathcal {G}}^N \times {\mathcal {D}}^N. \end{aligned}$$

Alternatively, for hierarchical permission structures³ in the disjunctive approach as introduced in Gilles and Owen (1994) (see also Gilles 2010) and van den Brink (1997) it is assumed that a non-top player needs permission from at least one of its predecessors. Therefore, a coalition is feasible if and only if for every player in the coalition (except the top player), at least one of its predecessors is also in the coalition. So, for permission structure D the set of disjunctive feasible coalitions is given by

$$\begin{aligned} \varPhi ^d_D = \left\{ E \subseteq N \left| P_D(i) \cap E \ne \emptyset \quad {\text {for all }} i \in E \setminus TOP(D) \right. \right\} . \end{aligned}$$

For every $E \subseteq N$, let $\sigma ^d_D(E) = \bigcup _{\{F \in \varPhi ^d_D \mid F \subseteq E\}} F$ be the largest disjunctive feasible subset⁴ of E in $\varPhi ^d_D$. Then, the induced disjunctive restricted game of the game with permission structure (v, D) is the game $r_{v,D}^d :2^{N}\rightarrow {\mathbb {R}}$ that assigns to every coalition $E \subseteq N$ the worth of its largest disjunctive feasible subset, i.e.

$$\begin{aligned} r_{v,D}^d (E) = v(\sigma ^d_D(E))\quad {\text {for all }} E \subseteq N. \end{aligned}$$

(2)

Then, the disjunctive (Shapley) permission value $\varphi ^d$ is the solution that assigns to every game with a permission structure the Shapley value of the disjunctive restricted game, thus

$$\begin{aligned} \varphi ^d(v,D) = Sh(r_{v,D}^d)\quad {\text {for all }} (v,D) \in {\mathcal {G}}^N \times {\mathcal {D}}^N_H. \end{aligned}$$

Example 1

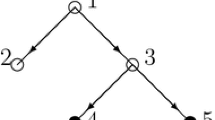
Consider the game with permission structure (v, D) on $N = \{1,2,3,4\}$ given by $v(E) = 1$ if $4 \in E$, $v(E) = 0$ if $4 \not \in E$, and $D=\{(1,2),(1,3),(2,4),(3,4)\}$ (see Fig. 1). The conjunctive feasible coalitions are: $\{1\},\ \{1,2\},\ \{1,3\},\ \{1,2,3\}$ and $\{1,2,3,4\}$. Additional⁵ disjunctive feasible coalitions are $\{1,2,4\}$ and $\{1,3,4\}$.

The conjunctive restriction is given by $r^c_{v,D}(E) = 1$ if $E = \{1,2,3,4\}$, and $r^c_{v,D}(E) = 0$ otherwise. Thus, $\varphi ^c(v,D) = (\frac{1}{4},\frac{1}{4},\frac{1}{4},\frac{1}{4})$. The disjunctive restriction is given by $r^d_{v,D}(E) = 1$ if $E \in \{\{1,2,4\},\ \{1,3,4\},\ \{1,2,3,4\}\}$, and $r^d_{v,D}(E) = 0$ otherwise. Thus, $\varphi ^d(v,D) = (\frac{5}{12},\frac{1}{12},\frac{1}{12},\frac{5}{12})$. $\square$

Fig. 1

Permission structure D of Example 1

In Example 1, without any restriction, according to the Shapley value in the unrestricted game, player 4 earns the full payoff of one, and the other players all earn zero. In the conjunctive approach, all three other players are necessary to make player 4 active and, therefore, the restricted game becomes the unanimity game of the grand coalition N, and the conjunctive permission value allocates the payoff equally over all four players, giving each a payoff of $\frac{1}{4}$. In the disjunctive approach, players 2 and 3 are not necessary to make player 4 active, although at least one of them is necessary. In the disjunctive permission value, this is reflected in the payoffs, where players 2 and 3 now get only $\frac{1}{5}$ of the payoffs of players 1 and 4 who both get the same payoff.

Which of the two approaches is most suitable? This depends on the application one has in mind. In general, to motivate solutions we provide axiomatizations, preferably ‘comparable’ axiomatizations which help in comparing different solutions.

2.3 Axiomatization of the permission values

Since in this paper we focus on the Shapley value, we refer to the conjunctive and disjunctive (Shapley) permission values often just as conjunctive and disjunctive permission values. Player $i \in N$ is inessential in game with permission structure (v, D) if i and all its subordinates are null players in game v, i.e. if $v(E) = v(E \setminus \{j\})$ for all $E \subseteq N$ and $j \in \{i\} \cup \widehat{S}_D(i)$. Player $i \in N$ is necessary in game v if $v(E) = 0$ for all $E \subseteq N \setminus \{i\}$.

Next, we mention some axioms of solutions for games with a permission structure. Efficiency and additivity are straightforward generalizations of TU-game solution axioms. The inessential player property requires that inessential players earn a zero payoff. The necessary player property requires that necessary players earn at least as much as any other player if the game is monotone. Notice that a necessary player is a ‘strong’ player in a monotone game.

Efficiency For every $v \in {\mathcal {G}}^N$ and $D \in {\mathcal {D}}^N$, it holds that $\sum _{i \in N} f_i(v,D) = v(N)$.

Additivity For every $v, w \in {\mathcal {G}}^N$ and $D \in {\mathcal {D}}^N$, it holds that $f(v+w,D) = f(v,D) + f(w,D)$.

Inessential player property For every $v \in {\mathcal {G}}^N$ and $D \in {\mathcal {D}}^N$, if $i \in N$ is an inessential player in (v, D) then $f_i(v,D) = 0$.

Necessary player property For every $v \in {\mathcal {G}}^N_M$ and $D \in {\mathcal {D}}^N$, if $i \in N$ is a necessary player in (N, v) then $f_i(v,D) \ge f_j(v,D) \ {\text { for all }} j \in N$.

Both permission values satisfy these four axioms. We obtain an axiomatization of the conjunctive permission value by adding the following axiom saying that in monotone games, players earn at least as much as their successors.

Structural monotonicity For every $v \in {\mathcal {G}}^N_M$ and $D \in {\mathcal {D}}^N$, if $j \in S_D(i)$ then $f_i(v,D) \ge f_j(v,D)$.

Theorem 1

(van den Brink and Gilles 1996) A solution f for games with a permission structure is equal to the conjunctive permission value $\varphi ^c$ if and only if it satisfies efficiency, additivity, the inessential player property, the necessary player property and structural monotonicity.

We remark that the axioms in all axiomatizations mentioned in this paper are logically independent.

For hierarchical permission structures, the disjunctive permission value satisfies all these axioms except structural monotonicity. In Example 1, according to the disjunctive permission value, player 2 earns $\frac{1}{12}$ while player 4 earns $\frac{5}{12}$, showing that structural monotonicity is not satisfied. Note that player 1 still earns at least as much as player 4, also according to the disjunctive permission value. For hierarchical permission structures, the disjunctive permission value satisfies the following weaker version of structural monotonicity.

We say that player $i \in N$ dominates player $j \in N$ completely if all directed ‘permission paths’ from the top-player $i_0$ to player j contain player i. We denote the set of players that player i dominates completely by $\overline{S}_D(i)$, i.e.

$$\begin{aligned} \overline{S}_D(i) = \left\{ j \in \widehat{S}_D(i) \left| \begin{array}{c} i {\text { belongs to every directed path from }} i_0 {\text { to }} j \end{array}\right. \right\} . \end{aligned}$$

Also, define $\overline{P}_D(i) = \{j \in \widehat{P}_D(i) \mid i \in \overline{S}_D(j)\}$. Weak structural monotonicity requires that a player earns at least as much as each of its complete subordinates.

Weak structural monotonicity For every $v \in {\mathcal {G}}^N_M$ and $D \in {\mathcal {D}}^N$, if $i \in N$ and $j \in \overline{S}_D(i)$, then $f_i(v,D) \ge f_j(v,D)$.

Further, the disjunctive permission value satisfies disjunctive fairness which states that deleting the arc between two players h and $j \in S_D(h)$ (with $|P_D(j)| \ge 2$) changes the payoffs of players h and j by the same amount. Moreover, also the payoffs of all players i that completely dominate player h change by this same amount⁶. For $D \in {\mathcal {D}}^N$, $h \in N$ and $j \in S_D(h)$, we denote the permission structure that is left after deleting the arc between h and j by $D_{-(h,j)} = D \setminus \{(h,j)\}$.

Disjunctive fairness For every $v \in {\mathcal {G}}^N$ and $D \in {\mathcal {D}}^N_H$, if $h \in N$ and $j \in S_D(h)$ with $|P_D(j)| \ge 2$, then $f_j(v,D) - f_j(v,D_{-(h,j)}) = f_i(v,D) - f_i(v,D_{-(h,j)})$ for all $i \in \{h\} \cup \overline{P}_D(h)$.

It can be verified from Example 1 that the conjunctive permission value does not satisfy disjunctive fairness. However, it satisfies the alternative conjunctive fairness which states that deleting the arc between two players h and $j \in S_D(h)$ (with $|P_D(j)| \ge 2$) changes the payoffs of player j and any other predecessor $g \in P_D(j) \setminus \{h\}$ by the same amount. Moreover, also the payoffs of all players that completely dominate the other predecessor g change by this same amount.

Conjunctive fairness For every $v \in {\mathcal {G}}^N$ and $D \in {\mathcal {D}}^N_H$, if $h, j, g \in N$ are such that $h \ne g$ and $j \in S_D(h) \cap S_D(g)$ then $f_j(v,D) - f_j(v,D_{-(h,j)}) = f_i(v,D) - f_i(v,D_{-(h,j)}) {\text { for all }} i \in \{g\} \cup \overline{P}_D(g).$

The axioms described above characterize the two (Shapley) permission values for games with a hierarchical permission structure.⁷

Theorem 2

On the class of games with a hierarchical permission structure:

• (i) (van den Brink 1997) a solution f is equal to the disjunctive permission value $\varphi ^d$ if and only if it satisfies efficiency, additivity, the inessential player property, the necessary player property, weak structural monotonicity and disjunctive fairness.

• (ii) (van den Brink 1999) a solution f is equal to the conjunctive permission value $\varphi ^c$ if and only if it satisfies efficiency, additivity, the inessential player property, the necessary player property, weak structural monotonicity and conjunctive fairness.

Theorem 2 gives comparable axiomatizations of the conjunctive and disjunctive permission values that differ in only one axiom. In particular, an axiom that reflects some kind of equal treatment with respect to certain players when deleting arcs.

If $D=\emptyset$ then there are no restrictions in coalition formation⁸ (and $\varPhi ^c_D=\varPhi ^d_D=2^N$) and the conjunctive and disjunctive restricted games are just equal to the original game v. Consequently, $\varphi ^c(v,D)=\varphi ^d(v,D)=Sh(v)$ in that case. Notice that the three axiomatizations discussed here give the same axiomatization of the Shapley value for TU-games in case one only considers the empty graph $D=\emptyset$. In that case, efficiency and additivity just boil down to the corresponding axioms for TU-game solutions. Since no player has subordinates, a player is inessential if and only if it is a null player and, thus, the inessential player property boils down to the null player property for TU-game solutions. The necessary player property does not depend on the permission structure anyway, and can be stated as well for TU-game solutions by requiring that a necessary player in a monotone game earns at least as much as any other player.⁹ Efficiency, additivity, the inessential (null) player property and the necessary player property then give uniqueness as in Shapley (1953). Note that structural monotonicity, disjunctive fairness and conjunctive fairness have no meaning when $D=\emptyset$.

The two fairness axioms that are mentioned above compare the effects of deleting the arc between players h and $j \in S_D(h)$ on the payoffs of players h and j, respectively, on the payoffs of players $g \in P_D(j) \setminus \{h\}$ and j. These properties do not compare the change in payoffs of players h and $g \in P_D(j) \setminus \{h\}$ after deleting the arc between h and j. The opposite change property states that deleting the arc between player h and $j \in S_D(h)$ (with $|P_D(j)| \ge 2$) changes the payoffs of the two predecessors h and $g \in P_D(j) \setminus \{h\}$ in opposite direction. The Shapley permission values do not satisfy this property.¹⁰ The Shapley permission values do satisfy this property if we restrict ourselves to monotone games. As shown in van den Brink (2010), the conjunctive and disjunctive Banzhaf permission values (obtained by applying the Banzhaf value¹¹ to the conjunctive and disjunctive restricted games, do satisfy this opposite change property. They even satisfy the stronger property of power split neutrality which requires that the sum of the payoffs of the two predecessors does not change.¹²

For monotone games, deleting the arc between two players does not increase the payoff of the predecessor on the arc according to both Shapley permission values. Also, deleting an arc does not decrease the payoff of any other predecessor of the successor on the arc. The effect for the successor on the deleted arc depends on the approach. According to the conjunctive permission value, the payoff of the successor does not decrease, but according to the disjunctive permission value it does not increase. This comes from a fundamental difference between the two approaches, where deleting an arc leads to more feasible coalitions in the conjunctive approach, but to less feasible coalitions in the disjunctive approach. In the conjunctive approach, deleting an arc means that the successor on this arc does not need permission from this predecessor anymore. In the disjunctive approach, deleting an arc means that the successor cannot use the permission from this predecessor anymore, so now needs permission from at least one of its other predecessors, which was also sufficient before deleting the arc. This gives a very different interpretation to an arc: in the disjunctive approach, an additional arc creates possibilities, but in the conjunctive approach an additional arc creates restrictions. In both approaches, the feasible coalitions that are lost or gained contain both players on the arc.

Theorem 3

(van den Brink 1999) For every hierarchical permission structure $D \in {\mathcal {D}}^N_H$ and $i, j \in N$ such that $(i,j) \in D$, it holds that $\varPhi ^c_D \subset \varPhi ^c_{D_{-(i,j)}}$ and $\varPhi ^d_{D_{-(i,j)}} \subset \varPhi ^d_D$.

In the following, we refer to a set of coalitions ${\mathcal {F}} \subseteq 2^N$ that can be the conjunctive (respectively disjunctive) feasible set corresponding to some acyclic permission structure, i.e. there is some acyclic permission structure D such that ${\mathcal {F}} = \varPhi ^c_D$ (respectively ${\mathcal {F}} = \varPhi ^d_D$) as a conjunctive (respectively disjunctive) feasible set.

3 Games on an antimatroid

Games with a permission structure are one way to model games with a hierarchical structure on the set of players. Are there other ways to model hierarchically structured player sets? In Algaba et al. (2003a, b, 2004), the structure on the player set is represented by an antimatroid.

3.1 Antimatroids

Antimatroids are a combinatorial structure introduced by Dilworth (1940) and studied by Edelman and Jamison (1985).

Definition 1

A set of feasible coalitions ${\mathcal {A}} \subseteq 2^N$ is an antimatroid on N if it satisfies

• 1. $\emptyset \in {\mathcal {A}}$

• 2. (Closed under union) If $E,F\in {\mathcal {A}}$ then $E\cup F\in {\mathcal {A}}$

• 3. (Accessibility) If $E\in {\mathcal {A}}$, $E\ne \emptyset$, then there exists an $i\in E$ such that $E\setminus \left\{ i\right\} \in {\mathcal {A}}$.

An antimatroid is a normal antimatroid if, additionally, it satisfies

• 4. (Normality) For every $i\in N$ there exists an $E\in {\mathcal {A}}$ such that $i\in E$.

Note that normality and union closedness imply that $N\in {\mathcal {A}}$. In the following, we refer to normal antimatroids simply as antimatroids. The conjunctive and disjunctive feasible sets corresponding to an acyclic permission structure are antimatroids.

Theorem 4

(Algaba et al. 2004) If D is an acyclic permission structure on N, then $\varPhi ^c_D$ and $\varPhi ^d_D$ are antimatroids on N.

Next question is if antimatroids are really more general than permission structures. First, we exactly characterize those antimatroids that can be the conjunctive or disjunctive feasible set of some permission structure. It turns out that conjunctive feasible sets are exactly those that are closed under intersection. These are well-known structures, also known as poset antimatroids.

Theorem 5

(Algaba et al. 2004) Let ${\mathcal {A}}$ be an antimatroid. There is an acyclic permission structure D such that ${\mathcal {A}} = \varPhi ^c_D$ if and only if $E\cap F\in {\mathcal {A}}$ for every $E,F\in {\mathcal {A}}$.

An alternative way to characterize poset antimatroids is by using paths. An extreme player of $E\in {\mathcal {A}}$ is a player $i\in E$ such that $E\setminus \{i\}\in {\mathcal {A}}$. So, extreme players are those players that can leave a feasible coalition E keeping feasibility. By accessibility, every feasible coalition has at least one extreme player. Coalition $E\in {\mathcal {A}}$ is a path in ${\mathcal {A}}$ if it has a unique extreme player. The path $E\in {\mathcal {A}}$ is a i-path in ${\mathcal {A}}$ if it has $i\in E$ as unique extreme player.

The paths form the basis of an antimatroid in the sense that every feasible coalition in an antimatroid is either a path, or can be written as the union of other feasible coalitions in the antimatroid. So, if we know the paths, then we generate the full antimatroid by applying the union operator.

Theorem 6

(Algaba et al. 2004) Let ${\mathcal {A}}$ be an antimatroid. There is an acyclic permission structure D such that ${\mathcal {A}} = \varPhi ^c_D$ if and only if for every player $i \in N$ there is a unique i-path in ${\mathcal {A}}$.

This theorem implies that a conjunctive feasible set (poset antimatroid) has exactly n paths, one for each player. In Example 1, the paths of players 1, 2, 3 and 4, respectively, are the (feasible) sets $\{1\}, \{1,2\}, \{1,3\}$ and $\{1,2,3,4\}$. Feasible coalition $\{1,2,3\}$ is the union of the paths $\{1,2\}$ and $\{1,3\}$.

Obviously, in a disjunctive feasible set there can be players that have more than one path. In Example 1, we see that $\{1,2,4\}$ and $\{1,3,4\}$ are both paths of player 4. On the other hand, typical for the disjunctive feasible set $\varPhi ^d_D$ is that, given a path, leaving out the unique extreme player, we have again a path, see for example the sequence of paths $\{1,2,4\},\ \{1,2\},\ \{1\}, \emptyset$ in Example 1. This is not satisfied by the conjunctive feasible set $\varPhi ^c_D$ since deleting the unique extreme player from the path $\{1,2,3,4\}$, we are left with $\{1,2,3\}$ which is not a path since both players 2 and 3 are extreme players (as we saw above, it is the union of the feasible coalitions $\{1,2\}$ and $\{1,3\}$). It turns out that this ‘path property’ is typical for disjunctive feasible sets. In fact, we need something stronger.

Theorem 7

(Algaba et al. 2004) Let ${\mathcal {A}}$ be an antimatroid. There is an acyclic permission structure D such that ${\mathcal {A}} = \varPhi ^d_D$ if and only if

• 1. Every path E has a unique feasible ordering, i.e. $E:=\left( i_{1}>\cdots >i_{t}\right)$ such that $\left\{ i_{1},\ldots ,i_{k}\right\} \in {\mathcal {A}}$ for all $1\le k\le t$. Furthermore, the union of these orderings for all paths is a partial ordering of N.

• 2. If E, F and $E\setminus \{i\}$ are paths such that the extreme player of F equals the extreme player of $E\setminus \{i\}$, then $F\cup \{i\}\in {\mathcal {A}}$.

Next, we show that antimatroids are really more general than permission structures by giving an example of an antimatroid that does not satisfy the properties of Theorems 6 and 7.

Example 2

(Ordered partition voting) Consider player set $N=\{1,2,3,4,5\}$. Suppose that the player set is partitioned into two levels: Level 1 consists of players 1, 2 and 3, while Level 2 consists of players 4 and 5. Suppose that all subsets of Level 1 are feasible, but every subset of Level 2 needs approval of a majority (two-player) coalition of Level 1. So, the set of feasible coalitions is

$$\begin{aligned} {\mathcal {A}}= \left\{ \begin{array}{l} \emptyset ,\{1\},\{2\},\{3\}, \{1,2\},\{1,3\},\{2,3\},\{1,2,3\},\\ \{1,2,4\},\{1,2,5\},\{1,3,4\},\{1,3,5\}, \{2,3,4\},\{2,3,5\},\\ \{1,2,3,4\},\{1,2,3,5\}, \{1,2,4,5\}, \{1,3,4,5\}, \{2,3,4,5\}, \{1,2,3,4,5\} \end{array}\right\} \end{aligned}$$

This is an antimatroid. However, it is not a conjunctive feasible set (poset antimatroid) since $\{1,2,4\}$, $\{1,3,4\}$ and $\{2,3,4\}$ are all paths of player 4. It is also not a disjunctive feasible set since taking out the unique extreme player (4) from the path $\{1,2,4\}$ gives coalition $\{1,2\}$ which is not a path. $\square$

It is not difficult to prove that the conjunctive and disjunctive approach coincides if and only if the permission structure is a forest.

Theorem 8

(Algaba et al. 2004) Let D be an acyclic permission structure. Then, $\varPhi ^c_D = \varPhi ^d_D$ if and only if $|P_D(i)| \le 1$ for all $i \in N$.

3.2 Cooperative games on an antimatroid

A game on an antimatroid is a triple $(N,v,{\mathcal {A}})$ where $v \in {\mathcal {G}}^N$ is a characteristic function, and ${\mathcal {A}}$ is an antimatroid on player set N. Since we take the player set to be fixed, we denote a game on an antimatroid just as a pair $(v,{\mathcal {A}})$. The antimatroid is the set of feasible coalitions in the game and, thus, reflects the restricted cooperation possibilities. Since the conjunctive and disjunctive feasible sets derived from an acyclic permission structure are antimatroids, this model generalizes the games with a permission structure.

By union closedness, every coalition has a unique largest feasible subset. For antimatroids, Korte et al. (1991) introduced the interior operator $int_{{\mathcal {A}}} :2^N \rightarrow {\mathcal {A}}$ that assigns to every set its largest feasible subset, i.e.

$$\begin{aligned} int_{{\mathcal {A}}}(E)=\bigcup _{\{F \in {\mathcal {A}} \mid F \subseteq E\}} F\quad {\text {for all }} E\subseteq N. \end{aligned}$$

Using this operator, we can easily generalize the definition of the conjunctive and disjunctive restricted game for games with a permission structure to games on antimatroids. The restriction of game v on antimatroid ${\mathcal {A}}$ is the game $v_{\mathcal {A}}$ that assigns to every coalition the worth of its largest feasible subset and, thus, is given by

$$\begin{aligned} v_{\mathcal {A}}(E) = v(int_{\mathcal {A}}(E)) {\text { for all }} E \subseteq N. \end{aligned}$$

Next, we mention some properties for TU-games that are inherited by the restricted game.¹³ Player $i \in N$ is an atom in antimatroid ${\mathcal {A}}$ if $\{i\} \in {\mathcal {A}}$. If all $i \in N$ are atoms in ${\mathcal {A}}$, then ${\mathcal {A}} = 2^N$ and $v_{\mathcal {A}} = v$ for all games v.

Theorem 9

(Algaba et al. 2004) Let ${\mathcal {A}}$ be an antimatroid and v be a monotone game on N. Then

• 1. $v_{\mathcal {A}}$ is monotone.

• 2. If v is superadditive, then $v_{\mathcal {A}}$ is superadditive.

• 3. If v is balanced, then $v_{\mathcal {A}}$ is balanced. In particular ${ Core}(v) \subseteq { Core}(v_{\mathcal {A}})$.

• 4. If v is totally balanced, then $v_{\mathcal {A}}$ is totally balanced.

• 5. If ${\mathcal {A}}$ has a unique atom, then $v_{\mathcal {A}}$ is monotone, superadditive and totally balanced.

Since the set of conjunctive and the set of disjunctive feasible coalitions in some acyclic permission structure are antimatroids, the above theorems also hold for (conjunctive and disjunctive) restricted games with an acyclic permission structure.

3.3 Axiomatization of the restricted Shapley value

A solution f for games on antimatroids assigns a payoff vector $f(v,{\mathcal {A}}) \in {\mathbb {R}}^N$ to every game on an antimatroid $(v,{\mathcal {A}})$ on N. We consider the solution $\varphi ^{Sh}$ that assigns, to every game on an antimatroid, the Shapley value of the restricted game, i.e.

$$\begin{aligned} \varphi ^{Sh}(v,{\mathcal {A}}) = Sh(v_{\mathcal {A}}) \end{aligned}$$

Next, we generalize the axioms that characterized the permission values in the previous section. The first three axioms are straightforward generalizations of the corresponding axioms for games with a permission structure discussed in the previous section.

Efficiency For every $v \in {\mathcal {G}}^N$ and antimatroid ${\mathcal {A}}$, it holds that $\sum _{i\in N}f_{i}\left( v,{\mathcal {A}}\right) =v(N)$.

Additivity For every $v, w \in {\mathcal {G}}^N$ and antimatroid ${\mathcal {A}}$, it holds that $f\left( v+w,{\mathcal {A}}\right) =f\left( v,{\mathcal {A}}\right) +f\left( w,{\mathcal {A}}\right)$.

Necessary player property For every $v \in {\mathcal {G}}^N_M$ and antimatroid ${\mathcal {A}}$, if $i \in N$ is a necessary player in monotone game v, then $f_{i}\left( v,{\mathcal {A}}\right) \ge f_{j}\left( v,{\mathcal {A}}\right)$ for all $j\in N$.

For antimatroids, an inessential player is a null player such that every player that is somehow dependent on this player in the coalition formation is also a null player. We consider a player j dependent on another player i in the coalition formation process if i is in at least one j-path. We denote by A(j) the set of j-paths for $j\in N$. Therefore, for antimatroid ${\mathcal {A}}$ on N define $\widehat{P}_{\mathcal {A}}(j)=\bigcup _{E\in A\left( j\right) }E$ as the set of players that are in at least one j-path. Player $i\in N$ is an inessential player in $(v,{\mathcal {A}})$ if player i and every player $j\in N$ such that $i\in \widehat{P}_{\mathcal {A}}(j)$ are null players in v.

Inessential player property For every $v \in {\mathcal {G}}^N$ and antimatroid ${\mathcal {A}}$, if $i\in N$ is an inessential player in $(v,{\mathcal {A}})$ then $f_{i}\left( v,{\mathcal {A}}\right) =0$.

For structural monotonicity, we require that a player i earns at least as much as any other player j such that i is in every j-path. For antimatroid ${\mathcal {A}}$ on N define $\overline{P}_{\mathcal {A}}(j)=\bigcap _{E\in A\left( j\right) }E$ as the set of players that are in every j-path.

Structural monotonicity For every $v \in {\mathcal {G}}^N_M$ and antimatroid ${\mathcal {A}}$, if $i\in \overline{P}_{\mathcal {A}}(j)$, then $f_{i}\left( v,{\mathcal {A}}\right) \ge f_{j}\left( v,{\mathcal {A}}\right)$.

Obviously, $\overline{P}_{\mathcal {A}}(j)\subseteq \widehat{P}_{\mathcal {A}}(j)$. Moreover, an antimatroid is a poset antimatroid if and only if $\widehat{P}_{\mathcal {A}}(j)=\overline{P}_{\mathcal {A}}(j)$ for all $j\in N$.

Finally, we generalize both conjunctive as well as disjunctive fairness by requiring that deleting a feasible coalition from an antimatroid, such that what is left is still an antimatroid, has the same effect on the payoffs of all players in the coalition that is deleted.¹⁴

Fairness For every $v \in {\mathcal {G}}^N$ and antimatroid ${\mathcal {A}}$, if $E\in {\mathcal {A}}$ is such that ${\mathcal {A}}\setminus \{E\}$ is an antimatroid on N, then

$$\begin{aligned} f_{i}\left( v,{\mathcal {A}}\right) -f_{i}\left( v,{\mathcal {A}}\setminus \{E\}\right) = f_{j}\left( v,{\mathcal {A}}\right) -f_{j}\left( v,{\mathcal {A}} \setminus \{E\}\right) {\text { for all }} i, j \in E. \end{aligned}$$

Theorem 10

(Algaba et al. 2003a) A solution f for games on antimatroids is equal to the restricted Shapley value $\varphi ^{Sh}$ if and only if it satisfies efficiency, additivity, the necessary player property, the inessential player property, structural monotonicity and fairness.

Recall that in the axiomatizations of the conjunctive and disjunctive permission values in the previous section, we found that the conjunctive permission value satisfied structural monotonicity, while the disjunctive permission value only satisfied weak structural monotonicity. Applying structural monotonicity for antimatroids as defined above to the conjunctive or disjunctive feasible sets yields weak structural monotonicity since we only compare the payoffs of a player j with a player i that is in every ‘permission path’ to the top.

Also, we saw that the conjunctive and disjunctive permission values differ with respect to the fairness axiom they satisfy: conjunctive fairness and, respectively, disjunctive fairness. Fairness for antimatroids as defined above generalizes both these fairness axioms. The difference is with respect to the changes in the conjunctive and disjunctive feasible set as a consequence of deleting an arc. As mentioned in Theorem 3, deleting an arc leads to more feasible coalitions in the conjunctive feasible set, and to less feasible coalitions in the disjunctive feasible set. But in both cases the two players on the deleted arc are in every coalition that appears, respectively disappears, from the set of feasible coalitions.

Besides the axiomatization using conjunctive fairness, Theorem 1 axiomatizes the conjunctive permission value by the stronger structural monotonicity (for games with a permission structure) and without fairness. Considering the conjunctive feasible set as an antimatroid, structural monotonicity (for antimatroids) is equivalent to both weak structural monotonicity as well as structural monotonicity (for games with a permission structure) since for conjunctive feasible sets every player j has a unique j-path, and thus $\overline{P}_{\varPhi ^c_D}(j)=\widehat{P}_{\varPhi ^c_D}(j)$. It turns out that deleting fairness from the above axiomatization yields an axiomatization of the restricted Shapley value (conjunctive permission value) on the class of poset antimatroids. This result also allows us to characterize the class of poset antimatroids (among the antimatroids) as those antimatroids where the Shapley value is characterized by the axioms without fairness.

Theorem 11

(Algaba et al. 2003a)

• (i) A solution f for games on poset antimatroids is equal to the restricted Shapley value $\varphi ^{Sh}$ if and only if it satisfies efficiency, additivity, the necessary player property, the inessential player property and structural monotonicity.

• (ii) Let ${\mathcal {A}}$ be an antimatroid on N. Then, ${\mathcal {A}}$ is a poset antimatroid if and only if $\varphi ^{Sh}\left( \cdot ,{\mathcal {A}} \right)$ is the unique solution satisfying efficiency, additivity, the necessary player property, the inessential player property and structural monotonicity.

Note that with part (ii) of this theorem, we used an axiomatization of a solution (the Shapley value) to characterize a class of structures (in this case the class of poset antimatroids among the antimatroids). Although not done very often, characterizing network structures as those where an axiomatization of the Shapley value is valid (i.e. gives uniqueness) can be a useful approach to learn more about network structures.

4 Communication versus hierarchies

4.1 Communication graphs

One of the most well-known restrictions on coalition formation are communication restrictions as introduced in Myerson (1977). In that model, there is a communication network on the set of players in a cooperative game and a coalition E is feasible if and only if the players in E are connected within this communication network. This communication network is represented as an undirected graph on the set of players.

An undirected graph is a pair (N, L) where N is the set of nodes and $L \subseteq \{\{i,j\}|i,j \in N,~i \ne j\}$ is a collection of subsets of N such that every element of L contains precisely two elements. The elements of L represent undirected bilateral communication links and are referred to as edges or links. Since the nodes in a graph represent the positions of players in a communication network, we refer to the nodes as players. A sequence of k different players $(i_1,\ldots ,i_k)$ is a path in (N, L) if $\{i_h,i_{h+1}\} \in L$ for $h=1,\ldots ,k-1$. Two distinct players i and j, $i \ne j$, are connected in graph (N, L) if there is a path $(i_1,\ldots ,i_k)$ with $i_1=i$ and $i_k=j$. A graph is connected if any two players are connected in the graph. For graph (N, L) and coalition $E \subseteq N$, the set $L(E) = \{\{i,j\} \in L| \{i,j\} \subseteq E\}$ is the set of links between players in E. A coalition $E \subseteq N$ is connected in graph (N, L) if (N, L(E)) is connected. A maximally connected subset of coalition E in (N, L) is called a component of E in that graph, i.e. $F \subseteq E$ is a component of E in (N, L) if and only if (i) F is connected in (N, L(E)) and (ii) for every $h \in E \setminus F$ the coalition $F \cup \{h\}$ is not connected in (N, L(E)).

A triple (N, v, L) with (N, v) a TU-game and (N, L) an undirected communication graph is called a communication graph game. Since we take the player set to be fixed, we denote a communication graph game (N, v, L) just by (v, L). In the communication graph game (v, L) on N, players can cooperate if and only if they are able to communicate with each other, i.e. a coalition E is feasible if and only if it is connected in (N, L). Then, the set of feasible coalitions in a communication graph game (v, L) is the set of coalitions ${\mathcal {F}}_L \subseteq 2^N$ given by

$$\begin{aligned} {\mathcal {F}}_L = \{E \subseteq N \mid E {\text { is connected in }} (N,L)\}. \end{aligned}$$

We refer to this set as the communication feasible set of communication graph (N, L). Myerson (1977) introduced the restricted game of a communication graph game (v, L) as the TU-game $(N,v_L)$ in which every feasible coalition E can earn its worth v(E). Whenever E is not feasible, it can earn the sum of the worths of its components in (N, L). Denoting the set of components of $E \subseteq N$ in (N, L) by $C_L(E)$, the restricted game $(N,v_L)$ corresponding to communication graph game (v, L) thus is given by¹⁵

$$\begin{aligned} v_{L}(E)=\sum _{F\in C_{L}(E)}v(F) \quad {\text {for all }} E \subseteq N. \end{aligned}$$

(3)

As solution, Myerson (1977) proposes to take for every communication graph game the Shapley value of the corresponding restricted game, a solution that is later named the Myerson value for communication graph games. Myerson (1977) also axiomatized this solution by the axioms of component efficiency (meaning that every component allocates its own worth among its members) and fairness (meaning that deleting an edge changes the payoffs of the two players on this edge equally).

Example 3

Consider the communication graph (N, L) on $N = \{1,\ldots ,5\}$ given by $L=\{\{1,2\},\{1,3\},\{2,4\}$, $\{3,4\},\{4,5\}\}$, see Fig. 2. Players 1 and 5 are connected by two paths: (1, 2, 4, 5) and (1, 3, 4, 5). Coalition $\{1,4,5\}$ has two components: $\{1\}$ and $\{4,5\}$. Considering the unanimity game $u_{\{1,5\}}$, we see that the only feasible coalitions containing the two unanimity players are $\{1,2,4,5\},\ \{1,3,4,5\}$ and N. Therefore, the Myerson value, obtained as the Shapley value of the restricted game $v_L = u_{\{1,2,4,5\}}+ u_{\{1,3,4,5\}} - u_N$, assigns payoffs $(\frac{3}{10},\frac{1}{20},\frac{1}{20},\frac{3}{10},\frac{3}{10})$. $\square$

Fig. 2

Communication graph (N, L) of Example 3

Le Breton et al. (1992) and Demange (1994, 2004), consider a restricted Core concept where coalitional stability is required only for feasible coalitions, i.e. they consider the solution $C(v,L) = \{x \in {\mathbb {R}}^N \mid \sum _{i \in F} x_i = v(F)$ for all $F \in C_L(N)$, and $\sum _{i \in E} x_i \ge v(E)$ for all $E \in {\mathcal {F}}_L\}$. They show that this set of Core payoff vectors is nonempty if the game is superadditive and the communication graph is cycle-free¹⁶’,¹⁷ respectively a tree.¹⁸ This is interesting since superadditivity of a game v does not guarantee the existence of a Core-stable payoff vector for v. Under the stronger convexity condition on the game, but weaker cycle-completeness ¹⁹ on the graph, van den Nouweland and Borm (1992) show that the restricted game is convex and, therefore, the Myerson value belongs to the Core of the restricted game.

4.2 Characterizing communication feasible sets

Let ${\mathcal {F}} \subseteq 2^N$ be an arbitrary feasible set. Since all singletons in a communication graph are connected, it follows that communication feasible sets arising from communication graphs contain the empty set and satisfy normality, i.e. every player belongs to at least one feasible set. Further, they also satisfy accessibility. They even satisfy the stronger property that every feasible coalition with two or more players has at least two players that can leave the coalition leaving behind a feasible coalition (2-accessibility). This is easy to see since pending players (i.e. players that have only one neighbour) always can be deleted. A cycle-free graph has at least two pending players: the ‘worst’ case is a line-graph but it still has two pending players. If there are cycles, there usually are more extreme players.

Communication feasible sets are not closed under union (as is illustrated by the two connected coalitions $\{1,2\}$ and $\{5\}$ in Example 3 which union is not connected). However, as shown by Algaba et al. (2001a), communication feasible sets satisfy the weaker union stability meaning that the union of two feasible coalitions that have a nonempty intersection is also feasible. It turns out that these two properties together with normality and the emptyset being feasible characterize the communication feasible sets.

Theorem 12

(van den Brink 2012) Let ${\mathcal {F}}\subseteq 2^{N}$ be a set of feasible coalitions. Then, ${\mathcal {F}}$ is the communication feasible set of some communication graph if and only if

• 1. $\emptyset \in {\mathcal {F}}$

• 2. (Union stability) If $E,F\in {\mathcal {F}}$ with $E \cap F \ne \emptyset$ then $E\cup F\in {\mathcal {F}}$

• 3. (2-Accessibility) If $E\in {\mathcal {F}}$, $|E| \ge 2$, then there exist $i, j \in E$, $i \ne j$, such that $E\setminus \left\{ i\right\} , E\setminus \left\{ j\right\} \in {\mathcal {F}}$.

• 4. (Normality) For every $i\in N$ there exists an $E\in {\mathcal {F}}$ such that $i\in E$.

Usually, the set of links L, being coalitions of size two, is considered as the basis of a communication graph. Note that by applying 2-accessibility we can generate these bilateral links from any communication feasible set. Also note that given 2-accessibility, normality implies that $\{i\}\in {\mathcal {F}}$ for all $i\in N$ as is the case for communication feasible sets. Given closedness under union, normality implies that $N\in {\mathcal {F}}$ as is the case for antimatroids. By adding additional properties on a communication feasible set, we can characterize some special classes of communication graphs that are often encountered in the economic and OR literature, such as line-graphs, cycle-complete graphs, cycle-free graphs and trees (for details we refer to van den Brink 2012). To mention one example, adding closedness under intersection (i.e. for any two feasible coalitions also their intersection is feasible) to the properties of Theorem 12 characterizes the communication feasible sets arising from cycle-complete communication graphs.

Comparing Theorem 12 with Definition 1, we conclude that communication feasible sets are characterized by similar properties that define hierarchical structures represented by normal antimatroids. To be specific, besides normality and feasibility of the empty set, both satisfy an accessibility and a union property. Obviously, 2-accessibility implies accessibility and thus communication feasible sets satisfy a stronger accessibility property. But since closedness under union implies union stability, antimatroids satisfy a stronger union property.

5 Games with a local permission structure

A different type of generalization of games with a permission structure is the games with a local permission structure. Many applications of games with a permission structure fall in the special class of peer group games being games with a permission structure where the game is additive and the digraph is a rooted tree. A digraph $T \in {\mathcal {D}}^N$ is a rooted tree on N if it is hierarchical (i.e. acyclic and quasi-strongly connected) and, moreover, $|P_D(i)|=1$ for all $i \in N \setminus \{i_0\}$. (Alternatively, a digraph is a rooted tree if it is hierarchical, and for every player $i \in N \setminus \{i_0\}$ there is a unique path from the top player to this player i.) Peer group games are also a special class of digraph games being games derived from digraphs with weights on the nodes and are used, for example, to rank nodes in a digraph such as ranking teams in sports competitions, ranking alternatives in a preference profile, or ranking webpages on the internet. In this section, we discuss a model that generalizes games with a permission structure as well as digraph games.

5.1 Peer group games and digraph games

Brânzei et al. (2002) define a peer group situation as a triple (N, a, T) where $N \subset {\mathbb {N}}$ is a set of players, $T \in {\mathcal {D}}^N$ is a rooted tree, and $a \in {\mathbb {R}}^N_+$ is a vector of nonnegative weights assigned to the players.²⁰ Again, since we take the player set N to be fixed, we denote a peer group situation just as a pair (a, T). To every peer group situation (a, T), they assign the peer group game $v^P_{a,T}$ given by $v^P_{a,T}(E) = \sum _{\mathop {\widehat{P}_T(i) \subseteq E}\limits ^{i \in E}} a_i$, $E \subseteq N$. In terms of unanimity games, a peer group game can be written as $v^P_{a,T} = \sum _{i \in N} a_iu_{\{i\} \cup \widehat{P}_T(i)}$.

In Brânzei et al. (2002), it is already mentioned that every peer group situation (a, T) can be seen as a game with a permission structure $(w^a,T)$ where the permission structure T is a rooted tree and the game $w^a$ is the additive game given by $w^a(E)=\sum _{i \in E} a_i$ for all $E \subseteq N$. Then, the peer group game is the conjunctive (or disjunctive) restricted game.²¹

Theorem 13

(Brânzei et al. 2002) For every peer group situation (a, T) it holds that $v^P_{a,T}=r^c_{w^a,T}$.

Another model of games with a digraph on the set of players is that of the (weighted) digraph games introduced in van den Brink and Borm (2002). An irreflexive weighted directed graph, shortly referred to as weighted digraph, is a triple $(N,\delta ,D)$ where $N \subset {\mathbb {N}}$ is a set of nodes, $D \in {\mathcal {D}}^N$ is an irreflexive digraph, and $\delta \in {\mathbb {R}}^N_+$ is a vector of nonnegative weights assigned to the nodes. The (weighted) digraph game corresponding to $(N,\delta ,D)$ is the game $(N,\overline{v}_{\delta ,D})$ where the players represent the nodes and the characteristic function is given by $\overline{v}_{\delta ,D}(E) = \sum _{\mathop {P_D(i) \subseteq E}\limits ^{i \in E}} \delta _i$, $E \subseteq N$. So, the worth of an arbitrary coalition $E \subseteq N$ of players (nodes) is the sum of the weights of the players in that coalition for whom all predecessors belong to the coalition. In terms of unanimity games, a digraph game can be written as $\overline{v}_{\delta ,D} = \sum _{i \in N} \delta _i u_{\{i\} \cup P_D(i)}$. Again, since we take the player set N to be fixed, we denote a weighted digraph and weighted digraph game on N as $(\delta ,D)$, respectively, $\overline{v}_{\delta ,D}$.

A peer group game is a special case of a digraph game where the digraph is transitive.

Theorem 14

(van den Brink and Dietz 2014) For every peer group situation (a, T), it holds that $v^P_{a,T}=\overline{v}_{a,tr(T)}$.

Since the conjunctive restricted game is the same for a game with permission structure (v, D) and that game v on the transitive closure tr(D), from the above two propositions we have the following corollary.

Corollary 1

For every peer group situation (a, T), it holds that $v^P_{a,T}=r^c_{w^a,T}=r^c_{w^a,tr(T)}=\overline{v}_{a,tr(T)}$.

In van den Brink and Borm (2002), a relational power measure assigning values to every node in a weighted digraph is obtained by applying the Shapley value to the associated weighted digraph game. This power measure is referred to as the $\beta$-measure and is given by²²

$$\begin{aligned} \beta _i(D) = Sh_i(\overline{v}_{\delta ,D}) = \sum _{j \in \{i\} \cup S_D(i)} \frac{\delta _j}{(|P_D(j)| + 1)}. \end{aligned}$$

Brânzei et al. (2002), van den Brink and Borm (2002) and van den Brink and Dietz (2014) also consider other solutions for peer group games and digraph games.

5.2 Locally restricted games

Comparing games with a permission structure with weighted digraph games, there are two essential differences, one considering the games and another considering the effect of the digraph on the restrictions in cooperation. First, games with a permission structure allow any game, but weighted digraph games only consider additive games. On the other hand, to have permission to cooperate, a player in a game with (conjunctive) permission structure needs permission from all its superiors, but in a weighted digraph game it needs permission only from its (direct) predecessors. Obviously, the digraph game associated with a transitive digraph equals the conjunctive restricted game of the corresponding additive game on that digraph as permission structure. In this section, we only follow the conjunctive approach.²³

Theorem 15

(van den Brink and Dietz 2014) For every weighted digraph $(\delta ,D)$, it holds that $\overline{v}_{\delta ,tr(D)}=r^c_{w^\delta ,D}$, where $w^\delta (E)=\sum _{i \in E} \delta _i$ for all $E \subseteq N$. In particular, if D is transitive then $\overline{v}_{\delta ,D}=r^c_{w^\delta ,D}$.

Next, we generalize the (weighted) digraph games as well as games with a permission structure in the sense that we consider pairs (v, D) where $v \in {\mathcal {G}}^N$ can be any game, $D \in {\mathcal {D}}^N$ can be any digraph, but every player needs permission only from its direct predecessors in order to cooperate. So, a player needs permission from its predecessors to cooperate with other players, but it can give permission to its own successors without permission from its predecessors.

For any $E \subseteq N$, let $\sigma ^l_D(E) = \{i \in E \mid P_D(i) \subseteq E\}$ be the subset of players in E for whom all predecessors also belong to E. We refer to this as the value generating set of coalition E in D. The locally restricted game $r^l_{v,D}$ associated with the pair $(v,D) \in {\mathcal {G}}^N \times {\mathcal {D}}^N$ is the game $r^l_{v,D}$ given by

$$\begin{aligned} r^l_{v,D} (E) = v(\sigma ^l_D(E))\quad {\text {for all }} E \subseteq N. \end{aligned}$$

(4)

An important difference with the conjunctive feasible coalitions is the fact that $\sigma ^l_D(\sigma ^l_D(E))$ need not be equal to $\sigma ^l_D(E)$.

Example 4

Consider the digraph D on $N =\{1,2,3\}$ given by $D=\{(1,2),(2,3)\}$. Then, $\sigma ^l_D(\{2,3\})=\{3\}$ but $\sigma ^l_D(\{3\})=\emptyset$. $\square$

Because of this, the cooperation structure cannot be described just by a set of feasible coalitions as in the models of the previous sections. In Example 4, the coalition $\{3\}$ can be considered not feasible, but there is a coalition, to be specific coalition $\{2,3\}$, such that $\{3\}$ is exactly the coalition that generates value. Therefore, we call $\{3\}$ a value generating set in D.

Theorem 16

(van den Brink and Dietz 2014) Let $(v,D) \in {\mathcal {G}}^N \times {\mathcal {D}}^N$ and $E \subseteq N$ be given.

• (i) For all F such that $\sigma ^c_D(E) \subseteq F \subseteq E$ it holds that $r_{v,D}^c (F) = v(\sigma ^c_D(E))$

• (ii) For all F such that $\sigma ^l_D(E) \cup P_D(\sigma ^l_D(E)) \subseteq F \subseteq E$ it holds that $r_{v,D}^l (F) = v(\sigma ^l_D(E))$

Part (i) implies that for conjunctive restricted games, if a coalition of players E is able to generate its own worth, then it does not need permission from players outside E to do so; value generation and permission imply one another. For this reason, this approach can be described in terms of sets of feasible coalitions $\varPhi ^c_D$. This is not the case for locally restricted games as reflected in part (ii). This part states that the value generating set of a coalition E can generate its worth together with its predecessors (which are in E), without these predecessors actually generating any value within this coalition themselves: these coalitions still earn the worth of $\sigma ^l_D(E)$. Note that a coalition containing the value generating set of E, but not all its predecessors, might generate a different worth. Although it is true that $\sigma ^l_D(F)=\sigma ^l_D(E)$ for all F such that $\sigma ^l_D(E) \cup P_D(\sigma ^l_D(E)) \subseteq F \subseteq E$, this does not necessarily hold for all F such that $\sigma ^l_D(E) \subseteq F \subseteq E$. This is an important difference between the ‘local’ and ‘standard’ conjunctive approach to games with a permission structure.

These two approaches still have in common that for all $F \subseteq E \setminus \sigma ^c_D(E)$ (respectively for all $F \subseteq E \setminus \sigma ^l_D(E)$) it holds that $r^c_{v,D}(F) = 0$ (respectively $r^l_{v,D}(F) = 0$).

Example 5

Consider the digraph D on $N =\{1,2,3\}$ given in Example 4, and the game $v=u_{\{3\}}$. For coalition $E=\{2,3\}$, we have that $\sigma ^l_D(E) \cup P_D(\sigma ^l_D(E)) = \{3\} \cup \{2\} = \{2,3\} = E$. However, taking $F = \{3\}$ we have $\sigma ^l_D(E) = F \subset E$, but $r^l_{v,D}(F)=v(\sigma ^l_D(F))=v(\emptyset ) = 0$ while $v(\sigma ^l_D(E))=v(\{3\})=1$. So, indeed the predecessor of the value generating set of $E=\{2,3\}$ is necessary to generate its worth. $\square$

Next, we introduce some notions to describe the value generation and permission in games with a local permission structure. For any $E \subseteq N$, we define $\overline{\alpha }^l_D(E) = \sigma ^l_D(E) \cup P_D(\sigma ^l_D(E))$ as the active set of E. These are the players that are necessary and sufficient to make the value generating set $\sigma ^l_D(E)$ of E active.

We call a set E locally feasible in D if $\overline{\alpha }^l_D(E) = E$. We denote the set of all locally feasible sets in D by $\varPsi _D$. So,

$$\begin{aligned} \varPsi _D=\{E \subseteq N \mid \overline{\alpha }_D(E)=E\}. \end{aligned}$$

Let the authorizing set of E be given by $\alpha ^l_D(E) = E \cup P_D(E)$, being the set of players in E together with all their predecessors. This is the set of players that is necessary and sufficient to make the players in E active. It is clear that for any coalition E, $\alpha ^l_D(E)$ is locally feasible.

Example 6

Consider the permission structure D of Example 4 and coalition $\{2,3\}$. We already saw that its value generating set is $\{3\}$. Its active set is $\overline{\alpha }^l_D(\{2,3\})=\{2,3\}$ since permission of 2 is necessary and sufficient to make its value generating set $\{3\}$ active. Its authorizing set is $\alpha ^l_D(\{2,3\})=\{1,2,3\}$ since player 1 is necessary to make player 2 active who is not value generating in $\{2,3\}$ but is still necessary to give permission to player 3. In this case, $\varPhi ^c_D=\{\{1\},\{1,2\},\{1,2,3\}\}$ and $\varPsi _D=\varPhi ^c_D \cup \{\{2,3\}\}$. $\square$

Again, the active sets and authorizing sets show the separation between value generation and permission which coincide in the standard conjunctive approach.

Theorem 17

(van den Brink and Dietz 2014) For every permission structure $D \in {\mathcal {D}}^N$, it holds that $\emptyset , N \in \varPsi _D$ and $\varPsi _D$ is closed under union.

The basic elements of $\varPsi _D$ are the sets $\{i\} \cup P_D(i),\ i \in N$. The other elements of $\varPsi _D$ can be written as the union of two or more basic elements. However, unlike conjunctive feasible sets, $\varPsi _D$ is not necessarily intersection closed.

Next, we argue that the locally restricted approach to games with a permission structure generalizes the conjunctive approach as well as digraph games. The conjunctive restricted game of a game with a permission structure equals the locally restricted game of that game on the transitive closure of the permission structure. A weighted digraph game equals the locally restricted game of the additive game determined by the weights and the digraph as permission structure.

Theorem 18

(van den Brink and Dietz 2014)

• (i) For every $(v,D) \in {\mathcal {G}}^N \times {\mathcal {D}}^N$, it holds that $r^c_{v,D} = r^l_{v,tr(D)}$. In particular, if $D \in {\mathcal {D}}^N$ is transitive, then $r^c_{v,D}=r^l_{v,D}$.

• (ii) For every weighted digraph $(\delta ,D)$, it holds that $\overline{v}_{\delta ,D} =r^l_{w^\delta ,D}$.

5.3 The local permission value

As a solution, van den Brink and Dietz (2014) consider the local (conjunctive) permission value $\varphi ^l$ being the solution that assigns to every game with a permission structure the Shapley value of the locally restricted game, i.e.

$$\begin{aligned} \varphi ^l(v,D) = Sh(r^l_{v,D})\quad {\text {for all }} (v,D) \in {\mathcal {G}}^N \times {\mathcal {D}}^N. \end{aligned}$$

From the axioms of Theorem 1, the local permission value $\varphi ^l$ satisfies efficiency, additivity, the necessary player property and the inessential player property. It does not satisfy structural monotonicity as shown by the following example.

Example 7

Consider the game with permission structures (v, D) on $N=\{1,2,3\}$ given by $D=\{(1,2),(2,3)\}$ and $v=u_{\{3\}}$. Then, $\varphi ^l(v,D)=(0,\frac{1}{2},\frac{1}{2})$, and thus player 2 earns more than player 1, although 2 is a successor of 1 and the game is monotone. $\square$

The local permission value satisfies a weaker version requiring the payoff of a player to be at least equal to the payoff of any of its successors in a monotone game if at least one of its successors is a necessary player.

Local structural monotonicity For every $v \in {\mathcal {G}}^N_M$ and $D \in {\mathcal {D}}^N$, if $i \in N$ and $j \in S_D(i)$ are such that there exists at least one $h \in S_D(i)$ who is a necessary player in v, then $f_i(v,D) \ge f_j(v,D)$.

As mentioned above, the local permission value does satisfy the inessential player property. It satisfies an even stronger version of the inessential player property, requiring the payoff of a null player to be zero as soon as all its successors, but not necessarily all its subordinates, are null players in the game. We say that player $i \in N$ is locally inessential in game with permission structure (v, D) if i and all its successors are null players in v, i.e. if $v(E) = v(E \setminus \{j\})$ for all $E \subseteq N$ and $j \in \{i\} \cup S_D(i)$.

Local inessential player property For every $v \in {\mathcal {G}}^N$ and $D \in {\mathcal {D}}^N$, if $i \in N$ is a locally inessential player in (v, D) then $f_i(v,D) = 0$.

It turns out that strengthening the inessential player property in this way and weakening structural monotonicity as done above characterize the local permission value.

Theorem 19

(van den Brink and Dietz 2014) A solution f for games with a local permission structure is equal to the local permission value $\varphi ^l$ if and only if it satisfies efficiency, additivity, the necessary player property, the local inessential player property, and local structural monotonicity.

Instead of using local structural monotonicity, we can strengthen the necessary player property by saying that a player earns at least as much as any other player if this player is necessary or has at least one necessary successor in a monotone game.

Strong necessary player property For every $v \in {\mathcal {G}}^N_M$ and $D \in {\mathcal {D}}^N$, if at least one of the players in $\{i\} \cup S_D(i)$ is a necessary player in v then $f_i(v,D) \ge f_j(v,D) \ {\text { for all }} j \in N$.

Theorem 20

(van den Brink and Dietz 2014) A solution f for games with a local permission structure is equal to the local permission value $\varphi ^l$ if and only if it satisfies efficiency, additivity, the strong necessary player property and the local inessential player property.

Another interesting difference between the conjunctive and local permission value is the following. Stated informally, the conjunctive permission value satisfies veto monotonicity meaning that if a predecessor is going to veto one of its successors, then this does not harm that predecessor. But the local permission value does not satisfy this property. This is because a player who is necessary but also has a necessary successor will share the payoff resulting from its own necessity with its predecessor. So, in case at least one of the successors of a player is necessary, it is better for that player not to be necessary since then it will still have its share in the payoff (because it needs to give permission to a necessary successor), but because the player itself is not necessary it does not have to share with its own predecessors.²⁴

6 Applications

Many applications of games with a permission structure are in the special class of peer group games mentioned in the previous section. Applications of peer group games are, e.g. polluted river games (Ni and Wang (2007) and Dong et al. (2012)), liability games (Dehez and Ferey 2013), the duals of airport games (Littlechild and Owen 1973), auction games (Graham et al. 1990) and ATM games (Bjorndal et al. 2004). From the many applications of games with a permission structure, we will briefly discuss two: auction games (which are an application of peer group games), and hierarchically structured firms.

6.1 Auction games

An allocation situation is a pair (N, V) where $N = \{1,\ldots ,n\}$ is a set of agents or players and $V \in {\mathbb {R}}^N_+$ is a vector which ith component $V_i \in {\mathbb {R}}_+$ is the non-negative valuation of player $i \in N$ with respect to some indivisible good. Because the good is indivisible, it can be allocated to only one of the players in N. The player who gets the good can compensate the others by giving them an amount of some numeraire good. We assume that all players value each unit of the numeraire good at the same value, normalized to be 1. Since we again take the set of players N fixed, we represent an allocation situation (N, V) just by its valuation vector V.

An allocation–compensation scheme for an allocation situation is a pair $(i,c) \in N \times {\mathbb {R}}^N_+$ where $i \in N$ denotes the player who gets the good and $c \in {\mathbb {R}}^N$, satisfying $\sum _{j \in N} c_j = 0$, is the vector of compensations. So $c_j$, $j \ne i$, is the amount of the numeraire good that player i gives to player j as compensation, and $c_i$ is the total compensation that has to be paid by i to the other players. The value of allocation–compensation scheme (i, c) is the vector $\phi (i,c) \in {\mathbb {R}}^N_+$ with $\phi _j(i,c) = c_j$ if $j \in N \setminus \{i\}$, and $\phi _i(i,c) = V_i + c_i$. Main question in such an allocation situation is who gets the indivisible good and what is a ‘fair’ way to compensate the others. Without loss of generality, we assume that $V_1 \le \ldots \le V_n$.

Such allocation problems can be ‘solved’ using auctions. Graham et al. (1990) describe a process of bidder ring formation in Second-price sealed-bid and English open auctions, where for every coalition $E \subseteq N$ of bidders they define a strategic two-player game between the ‘players’ E and $N \setminus E$.²⁵ They show that the dominant strategy of E in the Second-price sealed-bid auction game is to bid $v^*(E) = \max _{i \in E} V_i$, and for $N \setminus E$ a dominant strategy is to bid $v^*(N \setminus E) = \max _{j \in N \setminus E} V_j$.²⁶ From this, they derive the worth of coalition $E \subseteq N$ in the corresponding auction game v to be equal to

$$\begin{aligned} v(E) = \max \left\{ \max _{i \in E} V_i - \max _{j \in N \setminus E} V_j, 0\right\} . \end{aligned}$$

(5)

Note that this is a peer group game associated with the peer group situation (a, T) with $a_i=V_i-V_{i-1},\ i \in N$, with $V_0=0$, and $T=\bigcup _{k=2}^n \{(k,k-1)\} = \{(n,n-1), (n-1,n-2), \ldots , , (2,1)\}$. In terms of unanimity games, we have $v=\sum _{i \in N} (V_i-V_{i-1}) u_{\{i, i+1, \ldots , i_n\}}$. Applying the Shapley value to this game yields

$$\begin{aligned} Sh_i(v) = \sum _{j=1}^{i} \frac{V_j-V_{j-1}}{n-j+1}\quad \text{ for } \text{ all } i \in N. \end{aligned}$$

(6)

In Algaba et al. (2003a), the axioms of Theorem 1 are modified and it is shown that this gives uniqueness on the class of auction games. The axioms can be directly applied to auction situations, except additivity. Additivity can only be applied to two valuation vectors that have the same ordering of the players with respect to their valuations. Further, note that a player is an inessential player in the auction game if and only if its valuation is zero, and is a necessary player if and only if it has the maximal valuation. An allocation rule for auction situations is a function $f :{\mathbb {R}}^N_+ \rightarrow {\mathbb {R}}^N$ that assigns to every auction situation the value of an allocation–compensation scheme. We state the axioms directly in terms of the auction situation, and refer to the allocation rule $f^{Sh} :{\mathbb {R}}^N_+ \rightarrow {\mathbb {R}}^N$ that assigns to every valuation vector $V \in {\mathbb {R}}^N_+$ the Shapley value $Sh(v)$ of the associated auction game v as the Shapley rule.

An allocation rule f satisfies efficiency if for every allocation situation $V \in {\mathbb {R}}^N_+$, it holds that $\sum _{i \in N} f_i(V) = \max _{i \in N} V_i$. An allocation rule f satisfies restricted additivity if for every pair of allocation situations $V, W \in {\mathbb {R}}^N_+$ such that $V_i \ge V_j$ if and only if $W_i \ge W_j$ for all $i, j \in N$, it holds that $f(V+W) = f(V) + f(W)$. An allocation rule f satisfies the inessential player property if for every allocation situation $V \in {\mathbb {R}}^N_+$ and $i \in N$ such that $V_i=0$ it holds that $f_i(V) = 0$. An allocation rule f satisfies the necessary player property if for every allocation situation $V \in {\mathbb {R}}^N_+$ and $i \in N$ such that $V_i = \max _{j \in N} V_j$, it holds that $f_i(V) \ge f_j(V) \ {\text { for all }} j \in N$. An allocation rule f satisfies structural monotonicity if for every allocation situation $V \in {\mathbb {R}}^N_+$, if $V_i \ge V_j$ then $f_i(N,V) \ge f_j(N,V)$.

Theorem 21

(Algaba et al. 2003a) An allocation rule f for allocation situations is equal to the Shapley rule if and only if it satisfies efficiency, restricted additivity, the inessential player property, the necessary player property and structural monotonicity.

Auction games are dual airport games.²⁷ Oishi et al. (2016) discuss anti-duality relations between the classes of auction games, airport games, polluted river games and liability games. Similar as in games with a permission structure, there is an exogenous ordering on the player set in polluted river games (determined by the location along a river) and liability games (determined by the position in a sequence of wrongful acts). On the other hand, in airport games and auction games, the order is endogenously determined by the valuations (respectively costs) of the players. Therefore, on the class of polluted river games and liability games, the Shapley value satisfies additivity, while for auction games and airport games it only satisfies the weaker restricted additivity. Similar, the cost sharing problems of Moulin and Shenker (1992) can be modeled using peer group games (but with some adaptation), and axiomatizations of their serial cost sharing rule can be given, see also Albizuri et al. (2002).

Another class of peer group games is the class of star graph peer group games where the rooted tree is a star graph. Applications of this are, e.g the ATM games of Bjorndal et al. (2004).

6.2 Hierarchically structured firms

In van den Brink (2008) and van den Brink and Ruys (2008), games with a permission structure are applied to model hierarchically structured firms. This is a special class of games with a permission structure that are not peer group games.

Most firms have a hierarchical structure, and not all wages are equal. Within a particular hierarchical level, there can be wage differences because of differences in the importance of the tasks done or the scarcity of the labor inputs that are able to perform the different tasks. Besides these horizontal wage differences within levels, there are also vertical wage differences between different levels. As in most part of the firm literature, we assume that the firm has a tree structure. A hierarchically structured firm can be modeled by a game with a permission structure (N, v, D) where the set of players N represents the set of employees in the firm (workers and managers), v is a cooperative production game describing the potential production possibilities of the employees in the firm, and D is a rooted tree with root (top-player) $i_0$ representing the hierarchical structure of the firm. Since we take the firm structure to be fixed,²⁸ we represent a hierarchical production game as a pair (v, D).

By D having a tree structure, it follows that there always exist employees that have no successors. These employees are the workers in D and the set of workers in D is denoted by $W_D = \{i \in N \mid S_D(i) = \emptyset \}$. We assume that these workers operate the production process in the firm. The other employees are the managers or coordinators who do not actively produce but who coordinate the production process. The set of managers in D is denoted by $M_D = N \setminus W_D$. For a manager $i \in M_D$, the set $\overline{S}_D(i) = \widehat{S}_D(i) \cap W_D$ is the set of workers that are (directly or indirectly) subordinate to i. For notational convenience, we denote $\overline{S}_D(i) = \{i\}$ for every worker $i \in W_D$.

Since the production process is carried out by the workers in $W_D$, its power set is the domain of a (cooperative) production game $\overline{v} :2^{W_D} \rightarrow {\mathbb {R}}_+$. The value $\overline{v}(E) \in {\mathbb {R}}_+$ is the non-negative production output value that can be generated if exactly the workers in $E \subseteq W_D$ are active in the production process. So, it is assumed that every worker $i \in W_D$ can choose either to provide all its labor effort or to provide nothing at all. Alternatively, we can think that firm positions can be occupied by employees or be vacant.

We extend the production game $\overline{v}$ on the set of workers $W_D$ to a game $v \in {\mathcal {G}}^N$ on the set of all employees N by adding the managers as null players, i.e. $v \in {\mathcal {G}}^N$ is given by $v(E)=\overline{v}(E \cap W_D)$ for all $E \subseteq N$. The pair (v, D) is a game with permission structure and is referred to as a hierarchical production game on N. We require that a fully employed firm produces a positive production output value, i.e. $v(W_D)>0$. We also assume the production game to be convex.²⁹

A wage function $\varphi$ assigns a non-negative wage $\varphi _i(v,D)$ to every employee $i \in N$ in the corresponding hierarchical production game (v, D). We can apply any solution for games with a permission structure, in particular the Shapley permission value (note that again, the conjunctive and disjunctive permission value are the same since the hierarchy is a rooted tree.)

In the literature, it is often argued that the wage of a manager in a firm is at least as high as the wage of any of its subordinates. This property is expressed by structural monotonicity. Moreover, if the production game is also convex, then according to the permission value the wage of a manager does not exceed the sum of the wages of its successors.³⁰

Theorem 22

(van den Brink 2008) Consider a hierarchical production game (v, D) and manager $i \in M_D$.

• (i) If v is monotone then $\varphi ^{Sh}_i(v,D) \ge \varphi ^{Sh}_j(v,D)$ for all $j \in S_D(i)$;

• (ii) If v is monotone and convex then $\varphi ^{Sh}_i(v,D) \le \sum _{j \in S_D(i)} \varphi ^{Sh}_j(v,D)$.

If firm (v, D) has constant span of control, meaning that every manager has the same number of successors s, then Theorem 22 implies that the ratio between the wage of a manager and the average wage of its successors (if positive) lies between one and the span of control s. If moreover, the workers in $W_D$ are symmetric, meaning that $v(E) = v(F)$ for all $E, F \subseteq W_D$ with $|E| = |F|$, Theorem 22 yields the following corollary.

Corollary 2

For every hierarchical production game (v, D) with monotone and convex v, symmetric workers and constant span of control s, it holds that $1 \le \frac{\varphi ^{Sh}_i(v,D)}{\varphi ^{Sh}_j(v,D)} \le s$ for all $i \in M_D$ and $j \in S_D(i)$ with $\varphi ^{Sh}_j(v,D) > 0$.

The bounds in this corollary are often assumed in the literature, see, e.g. Williamson (1967). They are sharp bounds in the sense that there are hierarchical production games such that the inequalities are equalities. We first characterize two types of subordinates of a manager. Successor j of manager i is indispensable for i if every worker h that is coordinated by i, but not by j, does not increase the productivity of any set of workers that does not contain workers coordinated by j (or j if j itself is a worker), i.e. $j \in S_D(i)$ is indispensable for $i \in M_D$ if $\overline{v}(E) = \overline{v}(E \setminus \{h\})$ for every $h \in \overline{S}_D(i) \setminus \overline{S}_D(j)$ and every $E \subset W_D$ with $E \cap \overline{S}_D(j) = \emptyset$.

Second, worker h is a dummy worker if it increases the productivity of every set of workers by the value $v(\{h\})$ which it also can produce on its own, i.e. $h \in W_D$ is a dummy worker if $\overline{v}(E) = \overline{v}(E \setminus \{h\}) + \overline{v}(\{h\})$ for every $E \subseteq W_D$ with $h \in E$.

It turns out that a manager earns the same wage as one of its successors if this successor is indispensable for the manager. A manager earns the sum of the wages of its successors if all its subordinate workers are dummy workers.

Theorem 23

(van den Brink 2008) Consider a hierarchical production game (v, D) and manager $i \in M_D$.

• (i) If $j \in S_D(i)$ is indispensable for i in (v, D) then $\varphi ^{Sh}_i(v,D) = \varphi ^{Sh}_j(v,D)$;

• (ii) If every $h \in \overline{S}_D(i)$ is a dummy worker in (v, D) then $\varphi ^{Sh}_i(v,D) = \sum _{j \in S_D(i)} \varphi ^{Sh}_j(v,D)$.

Applied to the famous constant elasticity of substitution (CES) production functions, the wage difference increases with the substitutability of labor inputs.

Example 8

Applying the famous constant elasticity of substitution (CES) production functions yield the following production games. A production function with n inputs given by $f :{\mathbb {R}}^N_+ \rightarrow {\mathbb {R}}_+$ is a convex CES production function if there exists $\rho \in (0,1]$, $\gamma > 0$ and $\alpha _1, \ldots , \alpha _n > 0$ with $\sum _{i = 1}^{n} \alpha _i = 1$ such that $f(x) = \gamma \left( \sum _{i = 1}^n \alpha _i (x_i)^\rho \right) ^{\frac{1}{\rho }}$. The parameter $\gamma$ is a scale parameter and $\rho$ is a parameter expressing the substitutability of the inputs.³¹ In our model, the n inputs are the $|W_D|$ labor inputs. Then, $x_i \ge 0$ is the amount of labor that is provided by worker $i \in W_D$. Since we assume that workers can be either fully active or inactive, we represent the situation in which exactly the workers in the set $E \subseteq W_D$ are active by the labor input vector $x^E \in \{0,1\}^{|W_D|}$ given by $x^E_i = 1$ if $i \in E$, and $x^E_i = 0$ otherwise. Assuming symmetric workers (i.e. $\alpha _i=\frac{1}{n},\ i \in \{1,\ldots ,n\}$) and constant span of control, the CES production game then can be written as $\overline{v}_{\rho }(E) = \gamma \left( \frac{|E|}{|W_D|} \right) ^{\frac{1}{\rho }}$. For a hierarchical convex CES production game with constant span of control and symmetric workers, the results in this section imply that the ratio between the wage of a manager and the wage of each of its successors is equal to the span of control s in case we have a linear production game with substitutable labor inputs (i.e. $\rho =1$), while it is equal to one in case the production game is a Cobb–Douglas production game with indispensable labor inputs (i.e. $\rho \rightarrow 0$). $\square$

It turns out that the axioms of Theorem 1 also characterize the Shapley value as wage system for hierarchical production games.³² In the context of hierarchical production games, they boil down to the following. Efficiency boils down to budget neutrality for firms meaning that the sum of the wages equals the total production value $v(N)=v(W_D)$. Additivity now can be directly applied to hierarchical production games. (So, unlike auction games it need not be restricted because the hierarchical structure on the employees is fixed.) An employee i is an inessential employee in hierarchical production game (v, D) if and only if every worker that is coordinated by i, or i itself if it is a worker, does not add anything in the production process. The inessential employee property states that an inessential employee earns zero. A worker i is a necessary worker if without its labor effort nothing can be produced. The necessary worker property states that necessary workers always earn at least as much as any other employee in the firm in case the production game is monotone.

Theorem 24

(van den Brink 2008) A wage function f is equal to $\varphi ^{Sh}$ if and only if it satisfies budget neutrality, additivity, the inessential employee property, the necessary worker property and structural monotonicity.

7 Concluding remarks

This survey discussed several results on games with a permission structure and some generalizations and applications. We mainly focussed on solutions based on the Shapley value. Other solutions can be applied. For example, van den Brink (2010) applies the Banzhaf value to the conjunctive and disjunctive restricted games. Axiomatizations use collusion neutrality properties that are based on those of Haller (1994) for TU-games. Derks and Gilles (1995) consider the Core of the restricted games. Similar as the Myerson value for communication graph games need not be in the Core of the restricted game, also the conjunctive, respectively disjunctive, (Shapley) permission values need not be in the Core of the corresponding restricted game. For permission tree games (where the permission structure is a rooted tree but the game can be any game), van den Brink et al. (2015) introduce the Average Tree permission value, which is obtained by applying the Average tree solution (introduced in Herings et al. (2008) for cycle-free communication graph games) to the communication graph game $(r^c_{v,D},L_D)$ where $r^c_{v,D}$ is the conjunctive restricted game of (v, D) and $L_D$ is the undirected graph obtained from digraph D by ignoring the orientation of the arcs. They show that in case the original game is monotone, the Average Tree permission value belongs to the Core of the restricted game. Recently, other solutions for permission tree games are introduced in, e.g. van den Brink et al. (2016) and Álvarez-Mozos et al. (2015). Note that peer group games are a special case of permission tree games, and thus permission tree games seem to be very useful for applications.

Besides axiomatization, it turns out that games with a permission structure are also useful for computation of solutions for applications. For peer group games, Brânzei et al. (2005) provide a polynomial time algorithm for computing the nucleolus (Schmeidler 1969) of the restricted game. In van den Brink et al. (2010, 2011) polynomial time algorithms for two subclasses of games with a permission structure, both generalizing peer group situations, are developed. These algorithms also might help to axiomatically characterize the nucleolus for games with a permission structure. Next to axiomatization and computation, also strategic implementation of solutions for games with a permission structure is future research.

In this survey, we also discussed several generalizations of games with a permission structure, such as games on antimatroids and local permission structures. As mentioned, the restricted game approach is based on the fact that the conjunctive and disjunctive feasible sets, as any antimatroid, are union closed. In van den Brink et al. (2011), two different Shapley type values for games on union closed systems are introduced and axiomatized. For these systems, they only require them to be union closed (so they do not require accessibility), guaranteeing that every coalition has a unique largest feasible subset. Other models that generalize games with a permission structure are, e.g. the before mentioned games on union stable systems (see Algaba et al. 2000), games on augmenting systems (see Bilbao 2003; Bilbao and Ordoñez 2009 and Algaba et al. 2010), and games on regular set systems (see Honda and Grabisch (2006), Lange and Grabisch (2009) and Grabisch 2013). Another type of generalization is by considering more general forms of cooperation in coalitions, such as fuzzy coalitions in Gallardo et al. (2014) and Jiménez-Losada et al. (2010).

Instead of applying restricted games as done in the models discussed in this paper, an alternative way to take account of cooperation restrictions in cooperative games is to restrict the set of admissible permutations as done in Faigle and Kern (1992). Initially defined for partially ordered sets, also this approach has been generalized to more general structures.

As mentioned above, next to axiomatization of the Shapley permission values and other solutions, future research will be directed to strategic implementation and computation of solutions for games with a permission structure and its generalizations. Also relations with other models, such as the digraph games mentioned in Sect. 4, extend the possibilities of application, for example to ranking alternatives in a social choice situation, ranking teams in sports competitions and ranking webpages on the internet.