Skip to main content
SpringerLink
Log in

Bayesian model robustness via disparities

  • Original Paper
  • Published:
TEST Aims and scope Submit manuscript

Abstract

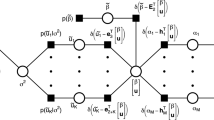
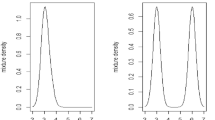
This paper develops a methodology for robust Bayesian inference through the use of disparities. Metrics such as Hellinger distance and negative exponential disparity have a long history in robust estimation in frequentist inference. We demonstrate that an equivalent robustification may be made in Bayesian inference by substituting an appropriately scaled disparity for the log likelihood to which standard Monte Carlo Markov Chain methods may be applied. A particularly appealing property of minimum-disparity methods is that while they yield robustness with a breakdown point of 1/2, the resulting parameter estimates are also efficient when the posited probabilistic model is correct. We demonstrate that a similar property holds for disparity-based Bayesian inference. We further show that in the Bayesian setting, it is also possible to extend these methods to robustify regression models, random effects distributions and other hierarchical models. These models require integrating out a random effect; this is achieved via MCMC but would otherwise be numerically challenging. The methods are demonstrated on real-world data.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  • Albert J (2008) LearnBayes: functions for learning Bayesian inference. R package version 2

  • Albert J (2009) Bayesian computation with R. Springer, New York

    Book  MATH  Google Scholar 

  • Andrade JAA, O’Hagan A (2006) Bayesian robustness modeling using regularly varying distributions. Bayesian Anal 1(1):169–188

    Article  MathSciNet  Google Scholar 

  • Basu A, Sarkar S, Vidyashankar AN (1997) Minimum negative exponential disparity estimation in parametric models. J Stat Plan Inference 58:349–370

    Article  MATH  MathSciNet  Google Scholar 

  • Basu A, Shioya H, Park C (2011) Statistical inference, monographs on statistics and applied probability, vol 120. CRC Press, Boca Raton (the minimum distance approach)

  • Beran R (1977) Minimum Hellinger distance estimates for parametric models. Ann Stat 5:445–463

    Google Scholar 

  • Berger JO (1994) An overview of robust Bayesian analysis. TEST 3:5–124

    Article  MATH  MathSciNet  Google Scholar 

  • Cheng AL, Vidyashankar AN (2006) Minimum Hellinger distance estimation for randomized play the winner design. J Stat Plan Inference 136:1875–1910

    Article  MATH  MathSciNet  Google Scholar 

  • Choy STB, Smith AFM (1997) On robust analysis of a normal location parameter. J Royal Stat Soc B 59:463–474

    Article  MATH  MathSciNet  Google Scholar 

  • Dawid AP (1973) Posterior expectations for large observations. Biometrika 60:664–667

    Article  MATH  MathSciNet  Google Scholar 

  • Desgagnè A, Angers JF (2007) Confilicting information and location parameter inference. Metron 65:67–97

    Google Scholar 

  • Devroye L, Györfi G (1985) Nonparametric density estimation: the L1 view. Wiley, New York

    Google Scholar 

  • Dey DK, Birmiwal LR (1994) Robust Bayesian analysis using divergence measures. Stat Prob Lett 20: 287–294

    Google Scholar 

  • Dunson DB, Taylor JA (2005) Approximate bayesian inference for quantiles. J Nonparametr Stat 17(3): 385–400

    Google Scholar 

  • Engel J, Herrmann E, Gasser T (1994) An iterative bandwidth selector for kernel estimation of densities and their derivatives. J Nonparametr Stat 4:2134

    Article  MathSciNet  Google Scholar 

  • Ghosh JK, Delampady M, Samanta T (2006) An introduction to Bayesian analysis. Springer, New York

    MATH  Google Scholar 

  • Hampel FR (1974) The influence curve and its role in robust estimation. J Am Stat Assoc 69:383–393

    Article  MATH  MathSciNet  Google Scholar 

  • Hampel FR, Ronchetti EM, Rousseeuw PJ, Stahel WA (1986) Robust statistics. Wiley Series in probability and mathematical statistics: probability and mathematical statistics. Wiley, New York (the approach based on influence functions)

  • Hansen BE (2004) Nonparametric conditional density estimation. http://www.ssc.wisc.edu/~bhansen/papers/ncde (Unpublished Manuscript)

  • Hoff PD (2007) Extending the rank likelihood for semiparametric copula estimation. Ann Appl Stat 1(1): 265–283

    Google Scholar 

  • Hooker G (2013) Consistency, efficiency and robustness of conditional disparity methods. arXiv:1307.3730

  • Huber P (1981) Robust statistics. Wiley, New York

    Book  MATH  Google Scholar 

  • Jiang W, Tanner MA (2008) Gibbs posterior for variable selection in high-dimensional classification and data mining. Ann Stat 26(5):2207–2231

    Article  MathSciNet  Google Scholar 

  • Jureckova J, Sen PK (1996) Robust statistical procedures. Wiley Series in probability and statistics: applied probability and statistics. Wiley, New York (asymptotics and interrelations, A Wiley-Interscience Publication)

  • Li Q, Racine JS (2007) Nonparametric econometrics. Princeton University Press, Princeton

    MATH  Google Scholar 

  • Lindsay BG (1994) Efficiency versus robustness: the case for minimum Hellinger distance and related methods. Ann Stat 22:1081–1114

    Article  MATH  MathSciNet  Google Scholar 

  • Maronna RA, Martin RD, Yohai VJ (2006) Robust statistics. Wiley Series in probability and statistics. Theory and methods. Wiley , Chichester

  • Nielsen M, Vidyashankar A, Hanlon B, Diao G, Petersen S, Kaplan R (2013) Hierarchical model for evaluating pyrantel efficacy against strongyle parasites in horses. Vet Parasitol 197(3):614–622

    Google Scholar 

  • O’Hagan A (1979) On outlier rejection phenomena in bayes inference. J Royal Stat Soc B 41:358–367

    MATH  MathSciNet  Google Scholar 

  • O’Hagan A (1990) Outliers and credence for location parameter inference. J Am Stat Assoc 85:172–176

    Article  MATH  MathSciNet  Google Scholar 

  • Park C, Basu A (2004) Minimum disparity estimation: asymptotic normality and breakdown point results. Bull Inf Cybernet 36:19–34

    Google Scholar 

  • Peng F, Dey DK (1995) Bayesian analysis of outlier problems using divergence measures. Can J Stat 23:199–213

    Article  MATH  Google Scholar 

  • Sheather SJ, Jones MC (1991) A reliable data-based bandwidth selection method for kernel density estimation. J Royal Stat Soc Ser B 53:683690

    MathSciNet  Google Scholar 

  • Silverman BW (1982) Density estimation. Chapman and Hall, Boca Raton

    Google Scholar 

  • Simpson DG (1987) Minimum Hellinger distance estimation for the analysis of count data. J Am Stat Assoc 82:802–807

    Article  MATH  Google Scholar 

  • Simpson DG (1989) Hellinger deviance test: efficiency, breakdown points and examples. J Am Stat Assoc 84:107–113

    Article  Google Scholar 

  • Sollich P (2002) Bayesian methods for support vector machines: evidence and predicive class probabilities. Mach Learn 46:21–52

    Article  MATH  Google Scholar 

  • Stigler SM (1973) The asymptotic distribution of the trimmed mean. Ann Stat 1:427–477

    MathSciNet  Google Scholar 

  • Szpiro AA, Rice KM, Lumley T (2010) Model-robust regression and a Bayesian “sandwich” estimator. Ann Appl Stat 4:2099–2113

    Article  MATH  MathSciNet  Google Scholar 

  • Tamura RN, Boos DD (1986) Minimum Hellinger distances estimation for multivariate location and and covariance. J Am Stat Assoc 81:223–229

    Article  MATH  MathSciNet  Google Scholar 

  • Wand M, Ripley B (2009) KernSmooth: functions for kernel smoothing. R package version 2.23-3

  • Wu Y, Hooker G (2013) Bayesian model robustness via disparities. arXiv:1112.4213

  • Zhan X, Hettmansperger TP (2007) Bayesian \(R\)-estimates in two-sample location models. Comput Statist Data Anal 51(10):5077–5089

    Article  MATH  MathSciNet  Google Scholar 

Download references

Acknowledgments

Giles Hooker’s research was supported by National Science Foundation grant DEB-0813734 and the Cornell University Agricultural Experiment Station federal formula funds Project No. 150446. Anand N. Vidyashankar’s research was supported in part by a grant from National Science Foundation, DMS-000-03-07057.

Author information

Authors and Affiliations

  1. Department of Biological Statistics and Computational Biology, Cornell University, Ithaca, USA

    Giles Hooker

  2. Department of Statistics, George Mason University, Fairfax, USA

    Anand N. Vidyashankar

Authors
  1. Giles Hooker
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Anand N. Vidyashankar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Giles Hooker.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary material 1 (pdf 292 KB)

Appendix

Appendix

Appendices A–F are available as Online Resource 1.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Hooker, G., Vidyashankar, A.N. Bayesian model robustness via disparities. TEST 23, 556–584 (2014). https://doi.org/10.1007/s11749-014-0360-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11749-014-0360-z

Keywords

Mathematics Subject Classification

Search

Navigation