1 Introduction

Time delays frequently appear in many practical systems, such as biological systems, chemical systems, electronic systems, network control systems, etc. The time delays are regarded as the major source of instability and poor performance. During the last two decades, the problem of stability of linear time-delay systems has been a subject of considerable research efforts. A great number of research results have been reported in [1–3]. The most commonly and frequently used state-space model of linear time-delay systems is

$$\dot x(t) = Ax(t) + Bx(t - \tau (t))$$
(1)

where τ(t) is the time-delay in the state x(t), which is often assumed to be constant or time-varying satisfying certain conditions, e.g., \(0 \leqslant \tau (t) \leqslant \tau ,\dot \tau (t) \leqslant d,\tau \) and d are positive constants. In the above mathematical model (1), the delay τ(t) in the state x(t) appears in a single form. However, in some practical situations, multiple delay components in the state should be considered, which can be found in the networked control systems. Thus, a new model for linear time-delay systems is proposed as

$$\dot x(t) = Ax(t) + Bx(t - \sum\limits_{i = 2}^n {{\tau _i}(t))} $$
(2)

Lam et al.[4] exposed the new model and gave a preliminary result on its stability analysis with two additive time-varying delay components. The introduction of model (2) is motivated by the observation that in some practical situations, signals transmitted from one point to another may experience new network segments, which can induce successive delays with different properties due to variable network transmission conditions, and this problem has been clearly justified by a state feedback remote control problem. An improved stability criterion was proposed by exploiting new Lyapunov-Krasovskii functional[5]. By taking more information of the time-varying delay in Lyapunov-Krasovskii functional into account and by utilizing free matrix variables in approximating certain integral terms, a new robust stability criterion for uncertain linear systems with two additive time-varying components was given[6]. Very recently, by using a delay decomposition method, a delay-dependent absolute stability condition for a class of nonlinear systems with two additive time-varying delay components is presented[7]. By constructing new Lyapunov-Krasovskii functionals and employing novel approaches to estimate the upper bound on the time derivative of the Lyapunov-Krasovskii functionals, some new delay-dependent stability criteria for linear systems and neural network with two additive time-varying components are derived[8 - 10].

On the other hand, during the past years, singular systems have attracted a lot of researchers from mathematics and control communities due to the fact that singular systems can describe the behavior of some physical systems better than regular systems. A great number of results based on the theory of regular systems have been extended to the area of singular systems[11]. Recently, much attention has been paid to singular systems with delay. It should be pointed that the stability problem for singular systems is much more complicated than that for regular systems because not only stability but also regularity and absence of impulses (for continuous singular systems)[12 - 17] or causality (for discrete singular systems)[18] should be considered. Note that the stability results mentioned in [12–18] can only provide stability conditions for singular systems with a single delay in state. However, to the best of our knowledge, stability conditions for singular systems with multiple delay components are few even non-existing in the published works, which has motivated this paper.

In this paper, we will propose a simple type of Lyapunov-Krasovskii functional and use the method inspired by [8, 9] to analyze the stability of singular systems with multiple delay components. A stability condition is established for the considered singular systems to be regular, impulse free, and stable. Based on this criterion, some new stability conditions for singular systems with a single delay in a range and regular systems with two additive time-varying delay components are also proposed. The main contribution of this paper is in three aspects. The first is to give a preliminary stability result for singular systems with two additive time-varying delay components. Second, the corollaries created by the result will involve fewer decision variables than existing ones, hence they are mathematically less complex and more computationally efficient. Third, the corollaries created by the result will be less conservative than some existing ones, which will be demonstrated by some numerical examples. As mentioned in [4,5], we still consider the case where only two additive time-varying components appear in the system state, and the idea in this paper can be extended to singular systems with multiple delay components.

Notations. Throughout this paper, Rn denotes the n-dimensional Euclidean space, while Rm × n refers to the set of all real matrices with m rows and n columns. A T represents the transpose of the matrix A, while A −1 denotes the inverse of A. For real symmetric matrices X and Y, the notation X ≥ Y (respectively, X > Y) means matrix X − Y is positive-semidefinite (respectively, positive-definite). I is the identity matrix with appropriate dimensions. ∥ x ∥ refers to the Euclidean norm of the vector x, i.e., \(\parallel x\parallel = \sqrt {{x^T}x.} *\) denotes the matrix entries implied by symmetry.

2 Problem statement

Consider the singular system with two additive time-varying delay components described by

$$\left\{ \begin{gathered} E\dot x(t) = Ax(t) + Bx(t - {\tau _1}(t) - {\tau _2}(t)) \hfill \\ x(t) = \varphi (t),t \in [ - \tau ,0] \hfill \\ \end{gathered} \right.$$
(3)

where x(t) ∈ R n is the state vector, and φ(t) ∈ R n denotes an initial function. The matrix E ∈ R n × n may be singular, and it is assumed that rank (E) = r ≤ n, A, B ∈ R n × n are the known matrices. τ 1(t) and τ 2(t) represent the two delay components in the state, it is assumed that

$$\begin{gathered} 0 \leqslant {\tau _i}(t) \leqslant {\tau _i} \hfill \\ {{\dot \tau }_i}(t) \leqslant {d_i} < \infty (i = 1,2) \hfill \\ \end{gathered} $$
(4)

and

$$\begin{gathered} \tau (t) = {\tau _1}(t){\tau _2}(t) \hfill \\ \tau = {\tau _1} + {\tau _2} \hfill \\ d = {d_1} + {d_2} \hfill \\ \end{gathered} $$

where τ i , d i (i = 1,2) are positive constants.

To this end, the following definitions and lemmas are recalled which will help in the discussion of our main results.

Definition 1[11]. The pair (E,A) is said to be regular if det(sE − A) is not identically zero. The pair (E,A) is said to be impulse free if deg(det(sE − A)) = rank(E).

Definition 2[12, 13]. The singular time-delay system (3) is said to be regular and impulse free if the pair (E, A) is regular and impulse free.

Definition 3[14, 16, 17]. The singular time-delay system (3) is said to be stable if for any ε > 0, there exists a scalar δ(ε) > 0 such that, for any compatible initial conditions φ(t) satisfying sup -τ ≤ t ≤ 0 ∥ φ(t) ∥ ≤ δ(ε), the solution x(t) of system (3) satisfies ∥ x(t) ∥ ≤ ε for any t ≥ 0, moreover, limt→∞ x(t) = 0.

Lemma 1[19]. For any x,y ∈ R n and any symmetric positive definite matrix R ∈ R n × n, the following inequality holds:

$$ - 2{x^T}y \leqslant {x^T}{R^{ - 1}}x + {y^T}Ry.$$

Lemma 2[20] (Schur complement). For a given symmetric matrix \(S = {S^T} = \left[ {\begin{array}{*{20}{c}} {{S_{11}}}&{{S_{12}}} \\ *&{{S_{22}}} \end{array}} \right]\) where S 11 ∈Rr × r, the following conditions are equivalent:

  1. 1)

    S < 0;

  2. 2)

    \({S_{11}} < 0,{S_{22}} - S_{12}^TS_{11}^{ - 1}{S_{12}} < 0;\)

  3. 3)

    \({S_{22}} < 0,{S_{11}} - {S_{12}}S_{22}^{ - 1}S_{12}^T < 0.\)

3 Main results

We provide a delay-dependent stability criterion guaranteeing the singular time-delay system (3) to be regular, impulse free and stable.

Theorem 1. Given scalars τ i > 0, d i > 0 (i = 1,2), for any delays τ 1 (t) and τ 2 (t) satisfying (4), the singular time-delay system (3) is regular, impulse free and stable, if there exist matrices P > 0, Q j > 0 (j = 1, 2, 3), R > 0 and X k , Y k , Z k , M k (k = 1, 2), such that linear matrix inequalities (LMIs) (5) - (8) hold.

$$\left[ {\begin{array}{*{20}{c}} \Xi &{\tau X} \\ *&{ - \tau R} \end{array}} \right] < 0$$
(5)
$$\left[ {\begin{array}{*{20}{c}} \Xi &{{\tau _1}X}&{{\tau _2}Y} \\ *&{ - {\tau _1}R}&0 \\ *&*&{ - {\tau _2}R} \end{array}} \right] < 0$$
(6)
$$\left[ {\begin{array}{*{20}{c}} \Xi &{{\tau _1}Z}&{{\tau _2}X} \\ *&{ - {\tau _1}R}&0 \\ *&*&{ - {\tau _2}R} \end{array}} \right] < 0$$
(7)
$$\left[ {\begin{array}{*{20}{c}} \Xi &{{\tau _1}Z}&{{\tau _2}Y} \\ *&{ - {\tau _1}R}&0 \\ *&*&{ - {\tau _2}R} \end{array}} \right] < 0$$
(8)

where

$$\begin{gathered} X = {[X_1^T\quad X_2^T\quad 0\quad 0]^T} \hfill \\ Y = {[Y_1^T\quad Y_2^T\quad 0\quad 0]^T} \hfill \\ Z = {[Z_1^T\quad Z_2^T\quad 0\quad 0]^T} \hfill \\ \Xi = \left[ {\begin{array}{*{20}{c}} {{\Xi _{11}}}&{{\Xi _{12}}}&{{Y_1}E - {Z_1}E}&{ - {X_1}E} \\ *&{{\Xi _{22}}}&{{Y_2}E - {Z_2}E}&{ - {X_2}E} \\ *&*&{ - (1 - {d_1}){Q_2}}&0 \\ *&*&*&{ - {Q_3}} \end{array}} \right] \hfill \\ \end{gathered} $$

with

$$[\begin{gathered} {\Xi _{11}} = {E^T}PA + {A^T}PE + {Q_1} + {Q_2} + {Q_3} + \tau {A^T}RA + {Z_1}E + {E^T}Z_1^T + {A^T}\Psi M_1^T + {M_1}{\Psi ^T}A \hfill \\ {\Xi _{12}} = {E^T}PB + \tau {A^T}RB + {X_1}E - {Y_1}E + {E^T}Z_2^T + {A^T}\Psi M_2^T + {M_1}{\Psi ^T}B \hfill \\ {\Xi _{13}} = - (1 - d){Q_1} + \tau {B^T}RB + {X_2}E + {E^T}X_2^T - {Y_2}E - {E^T}Y_2^T + {B^T}{\Psi ^T}B \hfill \\ \end{gathered} $$

and Ψ ∈ R n×(n−r) is any full-column rank matrix satisfying E TΨ = 0.

Proof. We first show that the singular time-delay system (3) is regular and impulse free for any delays τ 1(t),τ 2(t) satisfying (4). From LMIs (5) - (8), it is easy to see that

$${E^T}PA + {A^T}PE + {Z_1}E + {E^T}Z_1^T + {A^T}\Psi M_1^T + {M_1}{\Psi ^T}A < 0.$$
(9)

Since rank(E) = r ≤ n, there exist two nonsingular matrices G and H such that

$$GEH = \left[ {\begin{array}{*{20}{c}} {{I_r}}&0 \\ 0&0 \end{array}} \right].$$

Set

$$\begin{gathered} GEH = \left[ {\begin{array}{*{20}{c}} {{A_{11}}}&{{A_{12}}} \\ {{A_{21}}}&{{A_{22}}} \end{array}} \right] \hfill \\ {G^{ - T}}\Psi = \left[ {\begin{array}{*{20}{c}} 0 \\ {\tilde \Psi } \end{array}} \right] \hfill \\ {H^T}{M_1} = \left[ {\begin{array}{*{20}{c}} {{{\tilde M}_{11}}} \\ {{{\tilde M}_{12}}} \end{array}} \right] \hfill \\ \end{gathered} $$

where \(\tilde \Psi \in {R^{(n - r) \times (n - r)}}\) is a nonsingular matrix. Pre-multiplying and post-multiplying (9) by H T and H, respectively, and by some simple manipulations, we have

$$\left[ {\begin{array}{*{20}{c}} \# &\# \\ \# &{A_{22}^T\tilde \Psi \tilde M_{12}^T + {{\tilde M}_{12}}{{\tilde \Psi }^T}{A_{22}}} \end{array}} \right] < 0$$
(10)

where “#” represents matrices that are not relevant in the following discussion. From (10), we have

$$A_{22}^T\tilde \Psi \tilde M_{12}^T + {\tilde M_{12}}{\tilde \Psi ^T}{A_{22}} < 0$$

which implies matrix A 22 is nonsingular. Thus, the pair (E, A) is regular and impulse free. Hence, according to Definition 2, singular time-delay system (3) is regular and impulse free for any delays τ 1 (t) and τ 2 (t) satisfying (4).

Next, we will show that singular time-delay system (3) is stable. Choose the following Lyapunov-Karsovskii functional candidate

$$V(t) = {V_1}(t) + {V_2}(t) + {V_3}(t)$$
(11)

where

$$\begin{gathered} {V_1}(t){x^T}(t){E^T}PEx(t) \hfill \\ {V_2}(t) = \int_{t - r(t)}^t {{x^T}(s){Q_1}x(s)ds + } \int_{t - r1(t)}^t {{x^T}(s){Q_2}x(s)ds + \int_{t - r}^t {{x^T}(s){Q_3}x(s)ds} } \hfill \\ {V_3}(t) = \int_{t - r}^t {\int_\theta ^t {{{\dot x}^T}(s){E^T}\dot x(s)} dsd} \theta \hfill \\ \end{gathered} $$

with matrixes P, Q j (i = 1,2,3), R given in Theorem 1 satisfying LMIs (5) - (8).

Calculating the time derivatives of V i (t) (i = 1,2,3) along the trajectory of system (3) yields

$${\dot V_1}(t) = 2{x^T}(t){E^T}P(Ax(t) + Bx(t - \tau (t)))$$
(12)
$${\dot V_2}(t) = {x^T}(t)({Q_1} + {Q_2} + {Q_3})x(t) - (1 - \dot \tau (t)){x^T}(t - \tau (t)){Q_1}x(t - \tau (t)) - (1 - {\dot \tau _1}(t)){x^T}(t - \tau (t)){Q_2}x(t - \tau (t)) - {x^T}(t - \tau ){Q_3}x(t - r) \leqslant {x^T}(t)({Q_1} + {Q_2} + {Q_3})x(t) - (1 - d){x^T}(t - \tau (t)){Q_1}x(t - \tau (t)) - (1 - {d_1}){x^T}(t - {\tau _1}(t)){Q_2}x(t - {\tau _1}(t)) - {x^T}(t - \tau ){Q_3}x(t - \tau )$$
(13)
$${\dot V_3}(t) = \tau {\dot x^T}(t){E^T}RE\dot x(t) - \int_{t - r}^t {{{\dot x}^T}(s){E^T}RE\dot x(s)ds = } \tau {\dot x^T}(t){E^T}RE\dot x(t) - \int_{t - r}^{t - r(t)} {\dot xT(s){E^T}RE\dot x(s)ds - } \int_{t - r(t)}^{t - {r_1}(t)} {{{\dot x}^T}(s){E^T}RE\dot x(s)ds - } \int_{t - r1(t)}^t {{{\dot x}^T}(s){E^T}RE\dot x(s)ds.} $$
(14)

Defineξ ( t) = [x T(t) x T(t−τ(t)) x T(t−τ 1(t)) x T(t−τ)]T, from Lemma 1, the following inequalities (15) - (17) hold for matrices \(X = {[X_1^T\;X_2^T\;0\;0]^T},Y = {[Y_1^T\;Y_2^T\;0\;0]^T}\;and\,Z{[Z_1^T\;Z_2^T\;0\;0]^T}\) with appropriate dimensions.

$$ - \int_{t - r}^{t - r(t)} {{{\dot x}^T}(s){E^T}RE\dot x(s)ds \leqslant (\tau - \tau (t))\xi (t) + 2{\xi ^T}(t)XE(x(t - \tau (t)) - x(t - \tau )} $$
(15)
$$ - \int_{t - r(t)}^{t - r1(t)} {{{\dot x}^T}(s){E^T}RE\dot x(s)ds \leqslant {\tau _2}(t){\xi ^T}(t)Y{R^{ - 1}}{Y^T}\xi (t)} + 2{\xi ^T}(t)YE(x(t - {\tau _1}(t)) - x(t - \tau (t)))$$
(16)
$$ - \int_{t - r1(t)}^t {{{\dot x}^T}(s){E^T}RE\dot x(s)ds \leqslant {\tau _1}(t){\xi ^T}(t)Z{R^{ - 1}}{Z^T}\xi (t)} + 2{\xi ^T}(t)ZE(x(t) - x(t - {\tau _1}(t))).$$
(17)

It then follows from (14) - (17) that

$$\begin{gathered} {{\dot V}_3}(t) \leqslant \tau {(Ax(t) + Bx(t - \tau (t)))^T}R(Ax(t) + Bx(t - \tau (t))) + \hfill \\ {\xi ^T}(t)(({\tau _1} - {\tau _1}(t))X{R^{ - 1}}{X^T} + {\tau _1}(t)Z{R^{ - 1}}{Z^T} + \hfill \\ ({\tau _2} - {\tau _2}(t))X{R^{ - 1}}{X^T} + {\tau _1}(t)Z{R^{ - 1}}{Z^T} + \hfill \\ 2{\xi ^T}(t)(XE(x(t - \tau (t)) - x(t - \tau )) + \hfill \\ YE(x(t - {\tau _1}(t)) - x(t - \tau ))) + \hfill \\ ZE(x(t) - x(t - {\tau _1}(1)))). \hfill \\ \end{gathered} $$
(18)

On the other hand, for matrix \(M = {[M_1^T\quad M_2^T\quad 0\quad 0]^T}\) with appropriate dimensions, the following equation is true:

$$2{\xi ^T}(t)M{\Psi ^T}(Ax(t) + Bx(t - \tau (t))) = 0.$$
(19)

Combining (12), (13), (18) and (19), we can get

$$\begin{gathered} \dot V(t) \leqslant {\xi ^T}(t)\Xi + ({\tau _1} - {\tau _1})(t))X{R^{ - 1}}{X^T} + {\tau _1}(t)Z{R^{ - 1}}{Z^T} + \hfill \\ ({\tau _2} - {\tau _2}(t))X{R^{ - 1}}{X^T} + {\tau _2}(t)Y{R^{ - 1}}{Y^T})\xi (t). \hfill \\ \end{gathered} $$
(20)

Using the similar methods of [8, 9], (20) can be written as

$$\begin{gathered} \dot V(t) \leqslant {\xi ^T}(t)(\frac{{{\tau _1} - {\tau _1}(t)}}{{{\tau _1}}}\frac{{{\tau _2} - {\tau _2}(t)}}{{{\tau _2}}}(\Xi + {\tau _1}X{R^{ - 1}}{X^T}) + \hfill \\ \frac{{{\tau _1} - {\tau _1}(t)}}{{{\tau _1}}}\frac{{{\tau _2}(t)}}{{{\tau _2}}}(\Xi + {\tau _1}X{R^{ - 1}}{X^T} + {\tau _2}Y{R^{ - 1}}{Y^T}) + \hfill \\ \frac{{{\tau _1}(t)}}{{{\tau _1}}}\frac{{{\tau _2} - {\tau _2}(t)}}{{{\tau _2}}}(\Xi + {\tau _1}Z{R^{ - 1}}{Z^T} + {\tau _2}X{R^{ - 1}}{Y^T}) + \hfill \\ \frac{{{\tau _1}(t)}}{{{\tau _1}}}\frac{{{\tau _2}(t)}}{{{\tau _2}}}(\Xi + {\tau _1}Z{R^{ - 1}}{Z^T} + {\tau _2}Y{R^{ - 1}}{Y^T}))\xi (t) \hfill \\ \end{gathered} $$

using Lemma 2. From LMIs (5) - (8), it is easy to see that \(\dot V\)(t) < 0 for any x(t) ≠ 0. Hence, there exists a sufficiently small scalar ε > 0, such that

$$\dot V(t) \leqslant - \varepsilon \parallel x(t){\parallel ^2}$$

which implies that singular time-delay system (3) is stable[16, 17].

Remark 1. If we combine time-delays τ 1 (t) and τ 2 (t) into one delay τ(t), the stability of singular time-delay system (3) can be readily checked by using some existing conditions, such as [14, 16, 17]. However, as discussed in [4, 5], this approach would be inevitably conservative for some situations as it does not make full use of the information of τ 1 (t) and τ 2(t).

Remark 2. Though we only consider systems with two additive delay components, Theorem 1 can be readily extended to singular systems with multiple additive delay components, i.e.,

$$E\dot x(t) = Ax(t) + Bx(t - \sum\limits_{i - 3}^n {{\tau _i}} (t)).$$

When τ 1 (t) = τ 1, i.e., τ 1(t) is a constant delay, choosing

$$Z = {[ - \frac{1}{{{\tau _1}}}RE\quad 0\quad \frac{1}{{{\tau _1}}}RE\quad 0]^T}$$

in (17), we can obtain the following delay-dependent stability criterion from the procedure for the proof of Theorem 1.

Corollary 1. Given scalars τ 1 > 0,τ 2 > 0, d 2 > 0, for any delay τ 2(t) satisfying 0 ≤ τ 2(t) ≤ τ 2 and \(\dot \tau \)(t) ≤ d 2, the singular time-delay system (3) with τ 1(t) = τ 1 is regular, impulse free and stable, if there exist matrices P > 0, Qj > 0 (j = 1,2,3), R > 0 and X k , Y k , M k (k = 1,2,3), such that the following LMIs (21) - (22) hold:

$$\left[ {\begin{array}{*{20}{c}} \Upsilon &{{\tau _2}X} \\ *&{ - {\tau _2}R} \end{array}} \right] < 0$$
(21)
$$\left[ {\begin{array}{*{20}{c}} \Upsilon &{{\tau _2}Y} \\ *&{ - {\tau _2}R} \end{array}} \right] < 0$$
(22)

where

$$\begin{array}{*{20}{c}} {X = {{[X_1^T\;X_2^T\;0\;0]}^T}} \\ {Y = {{[Y_1^T\;Y_2^T\;0\;0]}^T}} \\ {\Upsilon = \left[ {\begin{array}{*{20}{c}} {{\Upsilon _{11}}}&{{\Upsilon _{12}}}&{{Y_1}E + \frac{1}{{{\tau _1}}}{E^T}RE}&{ - {X_1}E} \\ *&{{\Upsilon _{22}}}&{{Y_2}E}&{ - {X_2}E} \\ *&*&{ - {Q_2} - \frac{1}{{{\tau _1}}}{E^T}RE}&0 \\ *&*&*&{ - {Q_3}} \end{array}} \right]} \end{array}$$

with

$$\begin{array}{*{20}{c}} {{\Upsilon _{11}} = {E^T}PA + {A^T}PE + {Q_1} + {Q_2} + {Q_3} + \tau {A^T}RA - \frac{1}{{{\tau _1}}}{E^T}RE + {A^T}\Psi M_1^T + {M_1}{\Psi ^T}A} \\ {{\Upsilon _{12}} = {E^T}PB + \tau {A^T}RB + {X_1}E - {Y_1}E + {A^T}\Psi M_2^T + {M_1}{\Psi ^T}B} \\ {{\Upsilon _{22}} = - (1 - {d_2}){Q_1} + \tau {B^T}RB + {X_2}E + {E^T}X_2^T - {Y_2}E - {E^T}Y_2^T + {B^T}\Psi M_2^T + {M_2}{\Psi ^T}B} \end{array}$$

and Ψ ∈R n × (n−r) is any full-column rank matrix satisfying E TΨ = 0.

Remark 3. Note that when τ 1 (t) ≡ τ 1 is a constant delay, system (3) can be regarded as a class of singular systems with a single delay in a range[16, 17]: τ 1 ≤ τ(t) ≤ τ. Corollary 1 provide a new delay-dependent stability criterion for this class of singular time-delay systems.

If matrix E is nonsingular, then the stability problem of system (3) is reduced to analyzing the stability of the regular system

$$\left\{ \begin{gathered} \dot x(t) = Ax(t) + Bx(t - {\tau _1}(t) - {\tau _2}(t)) \hfill \\ x(t) = \varphi (t),\quad t \in [ - \tau ,0]. \hfill \\ \end{gathered} \right.$$
(23)

This problem has been widely studied in the recent literatures[4 - 8]. For the system (23), we choose the following Lyapunov-Krasovskii functional:

$$\begin{array}{*{20}{c}} {V(t) = {x^T}(t)Px(t) + \int_{t - \tau (t)}^t {{x^T}(s){Q_1}x(s)ds + } } \\ {\int_{t - {\tau _1}(t)}^t {{x^T}(s){Q_2}x(s)ds + \int_{t - \tau }^t {{x^T}(s){Q_3}x(s)ds + } } } \\ {\int_{t - \tau }^t {\int_\theta ^t {{{\dot x}^T}(s)R\dot x(s)dsd\theta } } } \end{array}$$
(24)

where P > 0, Q j > 0 (j = 1, 2, 3), R > 0.

From Theorem 1, we can obtain the following delay-dependent stability criterion for system (23).

Corollary 2. For given scalars τ > 0, d t > 0 (i = 1, 2), delays τ 1(t) and τ 2(t) satisfying (4), the time-delay system (23) is stable, if there exist matrices P > 0, Qj > 0 (j = 1,2,3), R > 0 and X k , Y k , Z k (k = 1,2), such that the following LMIs hold:

$$\left[ {\begin{array}{*{20}{c}} \Omega &{\tau X} \\ *&{ - \tau R} \end{array}} \right] < 0$$
(25)
$$\left[ {\begin{array}{*{20}{c}} \Omega &{{\tau _1}X}&{{\tau _2}Y} \\ *&{ - {\tau _1}R}&0 \\ *&*&{ - {\tau _2}R} \end{array}} \right] < 0$$
(26)
$$\left[ {\begin{array}{*{20}{c}} \Omega &{{\tau _1}Z}&{{\tau _2}X} \\ *&{ - {\tau _1}R}&0 \\ *&*&{ - {\tau _2}R} \end{array}} \right] < 0$$
(27)
$$\left[ {\begin{array}{*{20}{c}} \Omega &{{\tau _1}Z}&{{\tau _2}Y} \\ *&{ - {\tau _1}R}&0 \\ *&*&{ - {\tau _2}R} \end{array}} \right] < 0$$
(28)

where

$$\begin{array}{*{20}{c}} {X = {{[X_1^T\quad X_2^T\quad 0\quad 0]}^T}} \\ {Y = {{[Y_1^T\quad Y_2^T\quad 0\quad 0]}^T}} \\ {Z = {{[Z_1^T\quad Z_2^T\quad 0\quad 0]}^T}} \\ {\Omega = \left[ {\begin{array}{*{20}{c}} {{\Omega _{11}}}&{{\Omega _{12}}}&{{Y_1} - {Z_1}}&{ - {X_1}} \\ *&{{\Omega _{22}}}&{{Y_2} - {Z_2}}&{ - {X_2}} \\ *&*&{ - (1 - {d_1}){Q_2}}&0 \\ *&*&*&{ - {Q_3}} \end{array}} \right]} \end{array}$$

with

$$\begin{array}{*{20}{c}} {{\Omega _{11}} - PA + {A^T}P + {Q_1} + {Q_2} + {Q_3} + \tau {A^T}RA + {Z_1} + Z_1^T} \\ {{\Omega _{12}} = PB + \tau {A^T}RB + {X_1} - {Y_1} + Z_2^T} \\ {{\Omega _{22}} = - (1 - d){Q_1} + \tau {B^T}RB + {X_2} + X_2^T - {Y_2} - Y_2^T.} \end{array}$$

Remark 4. The obtained criteria in this paper are derived by defining the simple type of Lyapunov-Krasovskii functional (11) and (24), which not only make full use of the information about τ 1 (t) and τ 2(t), but also have fewer decision variables than the corresponding ones in some existing literatures[4–8,16–17]. Thus, our new proposed criteria are less conservative and the numerical complexity is smaller than some existing results, which will be demonstrated by numerical examples.

Remark 5. The conditions in Theorem 1, Corollaries 1 and 2 are all delay-dependent and rate-dependent. However, if we set Q 1 and Q 2 in them as zero, they reduce to delay-dependent and rate-independent ones, which can be used when the delay is not differentiable or the derivative of the delay is unknown.

Remark 6. The obtained results in this paper are formulated in terms of strict LMIs. It can be easily solved using any LMI toolbox, e.g, Matlab or Scilab.

4 Numerical examples

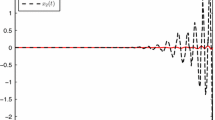
In this section, two numerical examples are used to illustrate that the proposed methods are effective and less conservative than some previous results.

Example 1. Consider singular time-delay system (3) with

$$\begin{array}{*{20}{c}} {E = \left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&0 \end{array}} \right]} \\ {A = \left[ {\begin{array}{*{20}{c}} {0.5}&0 \\ 0&{ - 1} \end{array}} \right]} \\ {B = \left[ {\begin{array}{*{20}{c}} { - 1.1}&1 \\ 0&{0.5} \end{array}} \right].} \end{array}$$

First, it is assumed that \(\dot \tau \)(t) ≤ 0.2, \(\dot \tau \) (t) ≤ 0.5. Our purpose is to find the upper bound τ of delay τ(t), when the delay τ 1 is known, such that the system is regular, impulse free and stable. The calculation results obtained by Theorem 1 in [14], Theorem 1 in [16], Theorem 1 in [17], and Theorem 1 in this paper for different cases are listed in Table 1. Next, it is assumed that τ 1(t) = τ 1, \(\dot \tau \)(t) ≤ 0.7. Our purpose is to find the upper bound τ of delay τ(t) when the delay τ 1 is known, such that the system is regular, impulse free and stable. The calculation results obtained by Theorem 1 in [16], Theorem 1 in [17], and Corollary 1 in this paper for different cases are listed in Table 2. It is clear that Theorem 1 and Corollary 1 in this paper gives much better results than those obtained by [14,16,17].

Table 1 Comparison of delay upper bound τ for various τ 1 and d 1 = 0.2, d 2 = 0.5
Full size table
Table 2 Comparison of delay upper bound τ for various τ 1 and d 1 =0,d 2= 0.7
Full size table

Example 2. Consider time-delay system (23)

$$\begin{array}{*{20}{c}} {A = \left[ {\begin{array}{*{20}{c}} { - 2}&0 \\ 0&{ - 0.9} \end{array}} \right]} \\ {B = \left[ {\begin{array}{*{20}{c}} { - 1}&0 \\ { - 1}&{ - 1} \end{array}} \right]} \\ {{{\dot \tau }_1}(t) \leqslant 0.1} \\ {{\tau _2}(t) \leqslant 0.8} \end{array}$$

Our purpose is to find the upper bound τ 2 of delay τ 2(t), or τ 1 of delay τ 1(t) when the delay τ 1 or τ 2 is known, such that the system is stable. The calculation results obtained by Theorem 1 in [4], Theorem 1 in [5], Theorem 1 in [6], Corollary 1 in [7], Theorem 1 in [8], and Corollary 2 in this paper for different cases are listed in Tables 3 and 4. It is clear that Corollary 2 in this paper gives much better results than those obtained by [4 - 7]. Moreover, the Corollary 2 in this paper contains fewer decision variables than those conditions in [4 - 8], which can be seen from Table 5. Hence, it is mathematically less complex and computationally more efficient.

Table 3 Comparison of delay upper bound τ 2 for various τ 1
Full size table
Table 4 Comparison of delay upper bound τ 1 for various τ 2
Full size table
Table 5 Number of decision variables
Full size table

5 Conclusions

This paper has investigated the stability problem for singular systems with two additive time-varying delay components. On the basis of a simple type of Lyapunov-Krasovskii functional and by utilizing free-weighting matrices, a delay-dependent stability criterion is established for the considered systems to be regular, impulse free, and stable in terms of LMIs. The obtained results can be used to deal with the problems of stability analysis for singular systems with single delay in a range and regular systems with two additive time-varying delay components. The resulting criteria have advantages over the previous ones because they involve fewer decision variables. Furthermore, they are less conservative than some existing ones. Two numerical examples are given to illustrate the applicability of the results.