1 Introduction

Deconvolution algorithms have been used to process data from a wide range of geophysical techniques, including for gravity, magnetic, and seismic data. Zuo and Hu (2012) also introduced a deconvolution algorithm for processing magnetotelluric data. However, the ringing artifacts produced by these deconvolution algorithms are rarely reported. Most of the research on ringing artifacts focuses on the enhancement of image compression techniques (Perona and Malik 1990; Weickert 1998; Pollak et al. 2000; Lysaker et al. 2003; Ding et al. 2005). Popovici and Withers (2007) proposed using a bilateral filter to suppress ringing artifacts from compressed images. The discrete wavelet transform algorithm was first used by Kim et al. (2009) to analyze ringing artifacts in multilevel edge maps for compressed images. These algorithms perform well for the suppression of ringing artifacts in compressed images, but are not suitable for processing deconvolution data from geophysical measurements.

The ringing artifacts that occur in the deconvolution of geophysical data are not the same as the artifacts in compressed images. In general, the ringing artifacts in deconvolution algorithms present as stronger oscillations than the artifacts in compressed images (Fig. 1).

Fig. 1
figure 1

a Ringing artifacts in a compressed image (Marziliano and Dufaux 2004). b Ringing artifacts produced during deconvolution of geophysical data (Zuo et al. 2009)

Full size image

The dotted lines L1 and L3 represent the same data selected from one row of observational data. Line L2 is the result of compressing L1 using the JPEG 2000 coded algorithm, while L4 is the result of deconvoluting L3.

Geophysical deconvolution algorithms introduce ringing artifacts as a result of errors in the observational data, and they commonly generate intense oscillations in areas of data discontinuity, e.g., edges and noise. They also often appear as false anomalous edges. The characteristics of the ringing artifacts seen after the deconvolution of geophysical data are very different from those of the ringing artifacts in compressed images. Therefore, it is not possible to directly suppress the ringing artifacts resulting from the deconvolution of geophysical data using traditional diffusion algorithms for compression images. Based on this analysis, we propose a novel method to suppress ringing artifacts arising from the deconvolution of geophysical data.

The discrete wavelet transform is a valuable signal analysis tool and can highlight specific subband features (Arivazhagan et al. 2007) through the decomposition of multiple scalars in complex data. Discrete wavelet transform is commonly applied for edge detections and contrast enhancements in various applications (Huang et al. 2002; Nakashizuka et al. 2004; Hatami et al. 2005). Pesquet et al. (1996) suggested using the stationary wavelet transform (SWT) algorithm to make the subband coefficients time invariant and to improve its power. In the SWT method, the coefficients have the same length as the original data at every level. It uses a stationary transform instead of traditional wavelet downsampling by adding an upsampling procedure on every scale coefficient (Gao et al. 2008). The redundancy of the SWT algorithm facilitates the detection of weak anomalies in the data, especially the detection of the false edges of ringing artifacts.

A nonlinear anisotropic diffusion method was proposed by Perona and Malik (1990) and has been widely studied in a number of scientific fields over the past two decades (Black et al. 1998; Pollak et al. 2000; Chen and Hsu 2005; Ding et al. 2005). The advantage of this method is that it can adaptively smooth noise while simultaneously preserving the actual model boundaries. Therefore, we used it to analyze ringing artifacts in the decomposed subbands of the SWT algorithm. In summary, we propose an anisotropic diffusion method to suppress the ringing artifacts in the results of the deconvolution of geophysical data based on SWT analysis.

The background to the SWT algorithm is briefly reviewed and then the proposed ringing artifact anisotropic filter based on the SWT algorithm is discussed. We describe our proposed multiresolution system and then present our experimental results and discussion before providing conclusions on our work.

2 Background to the SWT algorithm

Assuming H and G are the coefficients of the wavelet filters, then H [j](H [0] = H, j = 1, 2, …, n) and G [j](G [0] = G, j = 1, 2, …, n) can be obtained by inserting a zero between every adjacent pair of elements. If a 0 is an initial signal sequence, the signal stationary wavelet (Pesquet et al. 1996) is

$$\left\{ {\begin{array}{l} {a_{j + 1} = H^{[j]} a_{j} } \\ {b_{j + 1} = G^{[j]} b_{j} } \\ \end{array} }, \right.$$
(1)

where a j+1 represents the approximation coefficient of the SWT algorithm and b j+1 is the detail. We used a j (ɛ 1, …, ɛ j ) and b j (ɛ 1, …, ɛ j ) to denote the coefficients obtained from the SWT algorithm at level j

$$\phi_{j} (a_{j + 1} ,b_{j + 1} ) = H^{*} a_{j + 1} (\varepsilon_{j + 1} ) + G^{*} b_{j + 1} (\varepsilon_{j + 1} ),(\varepsilon_{j + 1} = 0),$$
(2)
$$\varphi_{j} (a_{j + 1} ,b_{j + 1} ) = H^{*} a_{j + 1} (\varepsilon_{j + 1} ) + G^{*} b_{j + 1} (\varepsilon_{j + 1} ),(\varepsilon_{j + 1} = 1),$$
(3)

where * represents a conjugate operator. The inverse SWT is

$$a_{j} (\varepsilon_{j} ) = \frac{1}{2}[\phi_{j} (a_{j + 1} ,b_{j + 1} ) + \varphi_{j} (a_{j + 1} ,b_{j + 1} )].$$
(4)

3 Ringing artifact anisotropic diffusion filter based on the SWT algorithm

The basic mechanism behind our approach can be analyzed by comparing the detailed SWT coefficients of the deconvolution results with the observed ringing artifacts (Fig. 2).

Fig. 2
figure 2

a Actual model. b Observation data. c Deconvolution results showing ringing artifacts. d Low-frequency wavelet coefficients LL 2. e High-frequency wavelet coefficients HL 1. f High-frequency wavelet coefficients HL 2

Full size image

LL 2 represents the output from the low-pass filter in the horizontal and vertical directions, whereas HL i are the outputs from the high-pass filter in the vertical and horizontal directions. All the high-frequency wavelet coefficients are magnified by a coefficient of 2 in this paper so that they can be more easily seen.

In Fig. 2d, the low-frequency wavelet coefficient LL 2 does not appear in any of the ringing artifacts, so it does not need to be filtered. However, Fig. 2e, f shows high levels of ringing artifacts in the decomposed high-frequency coefficients. In addition, the contrast in these coefficients increases as the level of decomposition k increases. A new anisotropic filter is suggested by this analysis, which works on the decomposed SWT coefficients as follows.

For a high-frequency wavelet coefficient H k (x, y) decomposed by the SWT algorithm and with a finite power and no zero values over the data support value Ω, k is the level of decomposition of the SWT algorithm k (k = 0, 1, 2, …, n). The output H k (x, y, t) can be expressed according to the following partial differential equation:

$$\left\{ {\begin{array}{l} {\frac{\partial }{\partial t}H_{k} (x,y,t) = \nabla \cdot [c(q)\nabla H_{k} (x,y,t)]} \\ {H_{k} (x,y,0) = H_{k} (x,y),(\partial H_{k} (x,y,t)/\partial \vec{n})|_{\partial \varOmega } = 0} \\ \end{array} }, \right.$$
(5)

where ∂Ω denotes the border of Ω and \(\partial \vec{n}\) is the outer normal of ∂Ω. A new diffusivity function c(q, k) is defined in Eq. (6):

$$c(q,k) = (1 + \sqrt k )/\{1 + [q^{2} (x,y,t,k) - q_{0}^{2} (t,k)]/[1 + q_{0}^{2} (t,k))]\},$$
(6)

where q(x, y, t, k) is the instantaneous coefficient determined by

$$q(x,y,t,k) = \sqrt {\frac{{(1/2)(|\nabla H_{k} /H_{k} |)^{2} - (1/16)(\nabla^{2} H_{k} /H_{k} )^{2} }}{{[1 + (1/4)(\nabla^{2} H_{k} /H_{k} )]^{2} }}}.$$
(7)

q(x, y, t, k) serves as the boundary detector for the data. The ringing artifact scale function q 0(t, k) is defined to control the degree of smoothing behavior as defined in Eq. (8):

$$q_{0} (t,k) = ({\overline{{\text{var}} (H_{k} (x,y,t))}})^{1/2}/\overline{{\text{mean}}(H_{k} (x,y,t))},$$
(8)

where \(\overline{{\text{var}}(\cdot)}\) and \(\overline{{\text{mean}}(\cdot)}\) are the mean of the intensity variance and the mean of the directions of the variants in the high-frequency wavelet coefficients decomposed by the SWT algorithm over a ringing artifact area, respectively.

The proposed anisotropic filter has some characteristics that are not shared with conventional anisotropic diffusion. In previous research on anisotropic filters, c(q) was equal to a Gaussian filter K σ as \(K_{\sigma } = \frac{1}{{2\pi \sigma^{2} }}\exp ( { - \frac{{|x|^{2} + |y|^{2} }}{{2\sigma^{2} }}})\) (Weickert 1998) and q 0(·) was defined as a domain function (Yu and Acton 2002). In this paper, Eqs. (6) and (8) define c(q, k), q(x, y, t, k), and q 0(t, k) in the wavelet domain without the assumption of a Gaussian distribution. Moreover, c(q, k), q(x, y, t, k), and q 0(t, k) are related to the SWT level of decomposition k.

As shown in Fig. 2, as the SWT level of decomposition k is increased, the contrast in the ringing artifact increases dramatically. The function c(q, k) then presents a high value and the proposed filter shows higher diffusion behavior as the SWT level of decomposition k is increased.

For a fixed level k, according to Eq. (6), the filter shows encouraging anisotropic diffusion in high-contrast edge regions where q(x, y, t, k) is larger than q 0(t, k). Otherwise, it acts as an isotropic filter over the ringing and non-edge regions.

Using the proposed anisotropic filter, the filter results for the decomposition of the high-frequency wavelet coefficients in Fig. 2d, f by the SWT algorithm are shown in Fig. 3.

Fig. 3
figure 3

a Filtering result for Fig. 2e. b Filtering result for Fig. 2f

Full size image

4 Multiresolution anisotropic diffusion

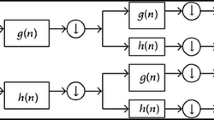
The proposed multiresolution ringing artifact anisotropic diffusion method is shown as a flow chart in Fig. 4. First, the deconvolution result is decomposed by the SWT algorithm, then the decomposed coefficients in every detailed subband are filtered by the proposed anisotropic filter. Finally, the inverse SWT algorithm is applied to the filtered results and the final result is the output.

Fig. 4
figure 4

Flow chart for SWT anisotropic diffusion treatment of ringing artifacts

Full size image

5 Results and discussion

To test the proposed anisotropic diffusion algorithm, the algorithm was applied to the synthetic model shown in Fig. 2a. The model was fitted by a Gaussian kernel \(K = e^{{ - (s_{1}^{2} + s_{2}^{2} )/(2\sigma^{2} )}} /\sum {\sum {e^{{ - (s_{1}^{2} + s_{2}^{2} )/(2\sigma^{2} )}} } }\)with a support size s 1 = s 2 = 6, σ = 2. The observation data are shown in Fig. 2b. A standard deconvolution algorithm was applied to the data with various values of point spread function support size bias (2, 4, 6, 8). The results of using our algorithm for deconvolution and diffusion are shown in Fig. 5.

Fig. 5
figure 5

Diffusion results for deconvolution. Comparison of results obtained by the proposed algorithm with those from other related algorithms. a Deconvolution results obtained with point spread function support size estimated bias values of 2, 4, 6, and 8, respectively. b Diffusion results obtained by the proposed algorithm. c Results from a filtered by a bilateral filter. d Results from a filtered by conventional anisotropic diffusion

Full size image

As Fig. 5a shows, the results of the proposed algorithm give a slightly low-pass effect. This phenomenon is due to the smoothing behavior of anisotropic diffusion. It is also clear that the discontinuities in the data are preserved during the diffusion procedure. Although the numerical range of the geophysical data and the common images are not the same, the characteristics of these ringing artifacts in these data are similar. Commonly, the textures of images are very complex, and its deconvolution result will contain complicated ringing artifact. So we discuss the suppression of the ringing artifact in images in the experiment section as the example. The geophysical data processing is similar to this procedure.

The effectiveness of the algorithm in suppressing ringing artifacts was evaluated by the mean absolute error (MAE) relative to the original model (Fig. 3a), as defined in Eq. (5):

$${\text{MAE}} = \frac{1}{\text{MN}}\sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{m} {|I(i,j,t) - I_{\text{ori}} |} } .$$
(5)

The results of the proposed SWT method based on multiresolution anisotropic diffusion are shown in Table 1. By comparing the results with those of the bilateral filter, it is easy to see that the numerical precision of the proposed SWT-based anisotropic diffusion results is higher than that for the bilateral filter, particularly when the ringing artifacts are strong. The proposed diffusion results also have a better visual quality. The bilateral filter results (Fig. 5c) seem to show fewer ringing artifacts and less blur than the proposed diffusion result (Fig. 5b). Based on the numerical statistical results in Table 1, it is easy to see that the data obtained using conventional anisotropic diffusion (Fig. 5d) are oversmoothed during filtering.

Table 1 Experimental and numerical statistical results
Full size table

The conventional diffusion and the bilateral filter did not preserve the weak edges. This behavior leads to a decrease in the actual model details, and some false edges appear in the results. In contrast, the proposed method avoids this behavior. Under the conditions of strong ringing artifacts (e.g., Fig. 5a, 4th image), the proposed anisotropic diffusion filter gives a better perceptual quality and numerical precision than the other filters. The MATLAB (version 2014b)-based programs were executed using an Intel i5-2500 k CPU, 3.30 GHz, 8.0 GB RAM system and the execution time for a 256 × 256 size model was <1 s.

6 Conclusions

This paper has introduced a diffusion algorithm that suppresses ringing artifacts for use in the postprocessing of deconvolution data from geophysical applications. The proposed anisotropic diffusion filter was able to simultaneously suppress the ringing artifacts and preserve the model boundaries. Experiments showed that this algorithm significantly enhanced both the visual and numerical static performance of the deconvolution results. This algorithm also worked well for the suppression of high-level ringing artifacts.