Skip to main content

Advertisement

SpringerLink
Log in

Segmentation of the proximal femur in radial MR scans using a random forest classifier and deformable model registration

  • Original Article
  • Published:
International Journal of Computer Assisted Radiology and Surgery Aims and scope Submit manuscript

Abstract

Background

Radial 2D MRI scans of the hip are routinely used for the diagnosis of the cam type of femoroacetabular impingement (FAI) and of avascular necrosis (AVN) of the femoral head, both considered causes of hip joint osteoarthritis in young and active patients. A method for automated and accurate segmentation of the proximal femur from radial MRI scans could be very useful in both clinical routine and biomechanical studies. However, to our knowledge, no such method has been published before.

Purpose

The aims of this study are the development of a system for the segmentation of the proximal femur from radial MRI scans and the reconstruction of its 3D model that can be used for diagnosis and planning of hip-preserving surgery.

Methods

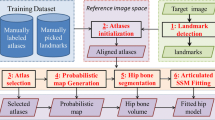
The proposed system relies on: (a) a random forest classifier and (b) the registration of a 3D template mesh of the femur to the radial slices based on a physically based deformable model. The input to the system are the radial slices and the manually specified positions of three landmarks. Our dataset consists of the radial MRI scans of 25 patients symptomatic of FAI or AVN and accompanying manual segmentation of the femur, treated as the ground truth.

Results

The achieved segmentation of the proximal femur has an average Dice similarity coefficient (DSC) of 96.37 ± 1.55%, an average symmetric mean absolute distance (SMAD) of 0.94 ± 0.39 mm and an average Hausdorff distance of 2.37 ± 1.14 mm. In the femoral head subregion, the average SMAD is 0.64 ± 0.18 mm and the average Hausdorff distance is 1.41 ± 0.56 mm.

Conclusions

We validated a semiautomated method for the segmentation of the proximal femur from radial MR scans. A 3D model of the proximal femur is also reconstructed, which can be used for the planning of hip-preserving surgery.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Chughtai M, Piuzzi NS, Khlopas A, Jones LC, Goodman SB, Mont MA (2017) An evidence-based guide to the treatment of osteonecrosis of the femoral head. Bone Jt J 99(10):1267–1279

    Article  Google Scholar 

  2. Sullivan JP, Griffith TB, Park CN, Ranawat AS (2017) Advances in 2D and 3D imaging for FAI surgical planning. In: Hip joint restoration. Springer, New York, pp 277–285

  3. Leunig M, Beaulé PE, Ganz R (2009) The concept of femoroacetabular impingement: current status and future perspectives. Clin Orthop Relat Res 467(3):616–622

    Article  PubMed  Google Scholar 

  4. Tannast M, Siebenrock KA, Anderson SE (2007) Femoroacetabular impingement: radiographic diagnosis—what the radiologist should know. Am J Roentgenol 188(6):1540–1552

    Article  Google Scholar 

  5. Steppacher SD, Huemmer C, Schwab JM, Tannast M, Siebenrock KA (2014) Surgical hip dislocation for treatment of femoroacetabular impingement: factors predicting 5-year survivorship. Clin Orthop Relat Res 472(1):337–348

    Article  PubMed  Google Scholar 

  6. Steppacher SD, Lerch TD, Gharanizadeh K, Liechti EF, Werlen SF, Puls M, Tannast M, Siebenrock KA (2014) Size and shape of the lunate surface in different types of pincer impingement: theoretical implications for surgical therapy. Osteoarthr Cartil 22(7):951–958

    Article  PubMed  CAS  Google Scholar 

  7. Lerch TD, Todorski IA, Steppacher SD, Schmaranzer F, Werlen SF, Siebenrock KA, Tannast M (2018) Prevalence of femoral and acetabular version abnormalities in patients with symptomatic hip disease: a controlled study of 538 hips. Am J Sports Med 46(1):122–134. https://doi.org/10.1177/0363546517726983

    Article  PubMed  Google Scholar 

  8. Morita D, Hasegawa Y, Okura T, Osawa Y, Ishiguro N (2017) Long-term outcomes of transtrochanteric rotational osteotomy for non-traumatic osteonecrosis of the femoral head. Bone Jt J 99(2):175–183

    Article  Google Scholar 

  9. Petchprapa CN, Dunham KS, Lattanzi R, Recht MP (2013) Demystifying radial imaging of the hip. Radiographics 33(3):E97–E112

    Article  PubMed  Google Scholar 

  10. Chana R, Noorani A, Ashwood N, Chatterji U, Healy J, Baird P (2006) The role of MRI in the diagnosis of proximal femoral fractures in the elderly. Injury 37(2):185–189

    Article  PubMed  CAS  Google Scholar 

  11. Cabarrus MC, Ambekar A, Lu Y, Link TM (2008) MRI and CT of insufficiency fractures of the pelvis and the proximal femur. Am J Roentgenol 191(4):995–1001

    Article  Google Scholar 

  12. Sutter R, Dietrich TJ, Zingg PO, Pfirrmann CW (2012) How useful is the alpha angle for discriminating between symptomatic patients with cam-type femoroacetabular impingement and asymptomatic volunteers? Radiology 264(2):514–521

    Article  PubMed  Google Scholar 

  13. Klenke FM, Hoffmann DB, Cross BJ, Siebenrock KA (2015) Validation of a standardized mapping system of the hip joint for radial MRA sequencing. Skelet Radiol 44(3):339–343

    Article  Google Scholar 

  14. Domayer SE, Mamisch TC, Kress I, Chan J, Kim YJ (2010) Radial dGEMRIC in developmental dysplasia of the hip and in femoroacetabular impingement: preliminary results. Osteoarthr Cartil 18(11):1421–1428

    Article  PubMed  CAS  Google Scholar 

  15. Zilkens C, Tiderius CJ, Krauspe R, Bittersohl B (2015) Current knowledge and importance of dGEMRIC techniques in diagnosis of hip joint diseases. Skelet Radiol 44(8):1073–1083

    Article  Google Scholar 

  16. Riley GM, McWalter EJ, Stevens KJ, Safran MR, Lattanzi R, Gold GE (2015) MRI of the hip for the evaluation of femoroacetabular impingement; past, present, and future. J Magn Reson Imaging 41(3):558–572

    Article  PubMed  Google Scholar 

  17. Schmaranzer F, Todorski IAS, Lerch TD, Schwab J, Cullmann-Bastian J, Tannast M (2017) Intra-articular lesions: imaging and surgical correlation. In: Seminars in musculoskeletal radiology, vol 21, No. 05. Thieme Medical Publishers, pp 487–506

  18. Schmaranzer F, Haefeli PC, Hanke MS, Liechti EF, Werlen SF, Siebenrock KA, Tannast M (2017) How does the dGEMRIC index change after surgical treatment for FAI? A prospective controlled study: preliminary results. Clin Orthop Relat Res 475(4):1080–1099

    Article  PubMed  Google Scholar 

  19. Rathnayaka K, Momot KI, Noser H, Volp A, Schuetz MA, Sahama T, Schmutz B (2012) Quantification of the accuracy of MRI generated 3D models of long bones compared to CT generated 3D models. Med Eng Phys 34(3):357–363

    Article  PubMed  Google Scholar 

  20. Lerch T, Degonda C, Zheng G, Todorski I, Schmaranzer F, Ecker T, Siebenrock K, Tannast M (2017) MR-based 3D PAO planning and simulation of hip impingement is as accurate as CT-based 3D models. German Congress of Orthopedic and Trauma Surgery (DKOU 2017)

  21. Xia Y, Fripp J, Chandra SS, Schwarz R, Engstrom C, Crozier S (2013) Automated bone segmentation from large field of view 3D MR images of the hip joint. Phys Med Biol 58(20):7375

    Article  PubMed  Google Scholar 

  22. Schmid J, Kim J, Magnenat-Thalmann N (2011) Robust statistical shape models for MRI bone segmentation in presence of small field of view. Med Image Anal 15(1):155–168

    Article  PubMed  Google Scholar 

  23. Gilles B, Magnenat-Thalmann N (2010) Musculoskeletal MRI segmentation using multi-resolution simplex meshes with medial representations. Med Image Anal 14(3):291–302

    Article  PubMed  Google Scholar 

  24. Arezoomand S, Lee WS, Rakhra KS, Beaulé PE (2015) A 3D active model framework for segmentation of proximal femur in MR images. Int J Comput Assist Radiol Surg 10(1):55–66

    Article  PubMed  Google Scholar 

  25. Chandra SS, Xia Y, Engstrom C, Crozier S, Schwarz R, Fripp J (2014) Focused shape models for hip joint segmentation in 3D magnetic resonance images. Med Image Anal 18(3):567–578

    Article  PubMed  Google Scholar 

  26. Zeng G, Yang X, Li J, Yu L, Heng PA, Zheng G (2017) 3D U-net with multi-level deep supervision: fully automatic segmentation of proximal femur in 3D MR images. In: International workshop on machine learning in medical imaging. Springer, Cham, pp 274–282

  27. Paiement A, Mirmehdi M, Xie X, Hamilton MC (2014) Integrated segmentation and interpolation of sparse data. IEEE Trans Image Process 23(1):110–125

    Article  PubMed  Google Scholar 

  28. Van Assen HC, Danilouchkine MG, Frangi AF, Ordás S, Westenberg JJ, Reiber JH, Lelieveldt BP (2006) SPASM: a 3D-ASM for segmentation of sparse and arbitrarily oriented cardiac MRI data. Med Image Anal 10(2):286–303

    Article  PubMed  Google Scholar 

  29. Tu Z (2008) Auto-context and its application to high-level vision tasks. In: IEEE conference on computer vision and pattern recognition, CVPR 2008. IEEE, pp 1–8

  30. Gao Y, Wang L, Shao Y, Shen D (2014) Learning distance transform for boundary detection and deformable segmentation in ct prostate images. In: International workshop on machine learning in medical imaging. Springer, Cham, pp 93–100

  31. Nyúl LG, Udupa JK, Zhang X (2000) New variants of a method of MRI scale standardization. IEEE Trans Med Imaging 19(2):143–150

    Article  PubMed  Google Scholar 

  32. Glocker B, Zikic D, Konukoglu E, Haynor DR, Criminisi A (2013) Vertebrae localization in pathological spine CT via dense classification from sparse annotations. In: International conference on medical image computing and computer-assisted intervention. Springer, Berlin, pp 262–270

  33. Criminisi A, Robertson D, Konukoglu E, Shotton J, Pathak S, White S, Siddiqui K (2013) Regression forests for efficient anatomy detection and localization in computed tomography scans. Med Image Anal 17(8):1293–1303

    Article  PubMed  CAS  Google Scholar 

  34. Schmid J, Magnenat-Thalmann N (2008) MRI bone segmentation using deformable models and shape priors. In: International conference on medical image computing and computer-assisted intervention. Springer, Berlin, pp 119–126

  35. Volino P, Magnenat-Thalmann N (2000) Implementing fast cloth simulation with collision response. In: Proceedings of the computer graphics international. IEEE, pp 257–266

  36. Cootes TF, Hill A, Taylor CJ, Haslam J (1993) The use of active shape models for locating structures in medical images. In: Biennial international conference on information processing in medical imaging. Springer, Berlin, pp 33–47

  37. Kraevoy V, Sheffer A (2006) Mean-value geometry encoding. Int J Shape Model 12(01):29–46

    Article  Google Scholar 

  38. Kumar S (2003) Discriminative random fields: a discriminative framework for contextual interaction in classification. In: Proceedings of the 9th IEEE international conference on computer vision, 2003. IEEE, pp 1150–1157

  39. Chu C, Chen C, Liu L, Zheng G (2015) Facts: fully automatic ct segmentation of a hip joint. Ann Biomed Eng 43(5):1247–1259

    Article  PubMed  Google Scholar 

  40. Yushkevich PA, Piven J, Hazlett HC, Smith RG, Ho S, Gee JC, Gerig G (2006) User-guided 3D active contour segmentation of anatomical structures: significantly improved efficiency and reliability. Neuroimage 31(3):1116–1128

    Article  PubMed  Google Scholar 

  41. Fedorov A, Beichel R, Kalpathy-Cramer J, Finet J, Fillion-Robin JC, Pujol S, Bauer C, Jennings D, Fennessy F, Sonka M, Buatti J (2012) 3D slicer as an image computing platform for the quantitative imaging network. Magn Reson Imaging 30(9):1323–1341

    Article  PubMed  PubMed Central  Google Scholar 

  42. Zikic D, Glocker B, Konukoglu E, Criminisi A, Demiralp C, Shotton J, Thomas OM, Das T, Jena R, Price SJ (2012) Decision forests for tissue-specific segmentation of high-grade gliomas in multi-channel MR. In: International conference on medical image computing and computer-assisted intervention. Springer, Berlin, pp 369–376

  43. Mahapatra D (2014) Analyzing training information from random forests for improved image segmentation. IEEE Trans Image Process 23(4):1504–1512

    Article  PubMed  Google Scholar 

  44. Montillo A, Shotton J, Winn J, Iglesias JE, Metaxas D, Criminisi A (2011) Entangled decision forests and their application for semantic segmentation of CT images. In: Biennial international conference on information processing in medical imaging. Springer, Berlin, pp 184–196

  45. Zikic D, Glocker B, Criminisi A (2014) Encoding atlases by randomized classification forests for efficient multi-atlas label propagation. Med Image Anal 18(8):1262–1273

    Article  PubMed  CAS  Google Scholar 

  46. Geremia E, Clatz O, Menze BH, Konukoglu E, Criminisi A, Ayache N (2011) Spatial decision forests for MS lesion segmentation in multi-channel magnetic resonance images. NeuroImage 57(2):378–390

    Article  PubMed  Google Scholar 

  47. Louppe G (2014) Understanding random forests: from theory to practice. arXiv Preprint arXiv:1407.7502

  48. Criminisi A, Shotton J (eds) (2013) Decision forests for computer vision and medical image analysis. Springer, Berlin

    Google Scholar 

  49. Damopoulos D, Glocker B, Zheng G (2017) Automatic localization of the lumbar vertebral landmarks in CT images with context features. In: International workshop and challenge on computational methods and clinical applications in musculoskeletal imaging. Springer, Cham, pp 59–71

  50. Breiman L (2001) Random forests. Mach Learn 45(1):5–32

    Article  Google Scholar 

  51. Kosov S (2013) Direct graphical models C++ library. http://research.project-10.de/dgm/

  52. Woolson RF (2007) Wilcoxon signed-rank test. Wiley, New York, pp 4739–4740. https://doi.org/10.1002/9780471462422.eoct979

    Book  Google Scholar 

  53. Li H, Johnson T (2014) Wilcoxon’s signed-rank statistic: what null hypothesis and why it matters. Pharmaceutical statistics 13(5):281–285

    Article  PubMed  Google Scholar 

  54. Sheskin DJ (2003) Handbook of parametric and nonparametric statistical procedures. CRC Press, Boca Raton

    Book  Google Scholar 

Download references

Funding

This study was funded by the Swiss National Science Foundation (Grant number 205321_163224).

Author information

Author notes

  1. Guoyan Zheng and Jérôme Schmid share the senior authorship

Authors and Affiliations

  1. Institute for Surgical Technology and Biomechanics, University of Bern, Stauffacherstrasse 78, 3014, Bern, Switzerland

    Dimitrios Damopoulos & Guoyan Zheng

  2. Department of Orthopaedic Surgery and Traumatology, Inselspital, University of Bern, Freiburgstrasse, 3010, Bern, Switzerland

    Till Dominic Lerch, Florian Schmaranzer & Moritz Tannast

  3. School of Health Sciences - Geneva, HES-SO University of Applied Sciences and Arts Western Switzerland, Avenue de Champel 47, 1206, Geneva, Switzerland

    Christophe Chênes & Jérôme Schmid

Authors
  1. Dimitrios Damopoulos
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Till Dominic Lerch
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Florian Schmaranzer
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Moritz Tannast
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Christophe Chênes
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Guoyan Zheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Jérôme Schmid
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Dimitrios Damopoulos or Guoyan Zheng.

Ethics declarations

Conflict of interest

All the authors declare that they have no conflict of interest.

Ethical approval

All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki Declaration and its later amendments or comparable ethical standards.

Informed consent

Informed consent was obtained from all individuals included in the study.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Damopoulos, D., Lerch, T.D., Schmaranzer, F. et al. Segmentation of the proximal femur in radial MR scans using a random forest classifier and deformable model registration. Int J CARS 14, 545–561 (2019). https://doi.org/10.1007/s11548-018-1899-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11548-018-1899-z

Keywords

Search

Navigation