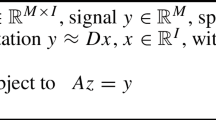Abstract
Recently, the 1-bit compressive sensing (1-bit CS) has been studied in the field of sparse signal recovery. Since the amplitude information of sparse signals in 1-bit CS is not available, it is often the support or the sign of a signal that can be exactly recovered with a decoding method. We first show that a necessary assumption (that has been overlooked in the literature) should be made for some existing theories and discussions for 1-bit CS. Without such an assumption, the found solution by some existing decoding algorithms might be inconsistent with 1-bit measurements. This motivates us to pursue a new direction to develop uniform and nonuniform recovery theories for 1-bit CS with a new decoding method which always generates a solution consistent with 1-bit measurements. We focus on an extreme case of 1-bit CS, in which the measurements capture only the sign of the product of a sensing matrix and a signal. We show that the 1-bit CS model can be reformulated equivalently as an ℓ 0-minimization problem with linear constraints. This reformulation naturally leads to a new linear-program-based decoding method, referred to as the 1-bit basis pursuit, which is remarkably different from existing formulations. It turns out that the uniqueness condition for the solution of the 1-bit basis pursuit yields the so-called restricted range space property (RRSP) of the transposed sensing matrix. This concept provides a basis to develop sign recovery conditions for sparse signals through 1-bit measurements. We prove that if the sign of a sparse signal can be exactly recovered from 1-bit measurements with 1-bit basis pursuit, then the sensing matrix must admit a certain RRSP, and that if the sensing matrix admits a slightly enhanced RRSP, then the sign of a k-sparse signal can be exactly recovered with 1-bit basis pursuit.
Similar content being viewed by others
References
Ai A, Lapanowski A, Plan Y, et al. One-bit compressed sensing with non-gaussian measurements. Linear Algebra Appl, 2014, 441: 222–239
Bahmani S, Boufounos P T, Raj B. Robust 1-bit compressive sensing via gradient support pursuit. TR2013-029, Mitsubishi Electric Research Lab, April 2013
Bandeira A, Dobriban E, Mixon D, et al. Certifying the restricted isometry property is hard. IEEE Trans Inform Theory, 2013, 59: 3448–3450
Boufounos P. Greedy sparse signal reconstruction from sign measurements. In: Proceedings of the 43rd Asilomar Conference on Signals, Systems And Computers. Piscataway: IEEE Press, 2009, 1305–1309
Boufounos P. Reconstruction of sparse signals from distorted randomized measurements. In: 2010 IEEE International Conference on Acoustics, Speech and Signal Processing. New York: IEEE, 2010, 3998–4001
Boufounos P, Baraniuk R. 1-Bit compressive sensing. In: Conference on Information Sciences Systems. New York: IEEE, 2008, 16–21
Bourquard A, Aguet F, Unser M. Optical imaging using binary sensors. Opt Express, 2010, 18: 4876–4888
Bourquard A, Unser M. Binary compressed imaging. IEEE Trans Image Process, 2013, 22: 1042–1055
Bruckstein A, Elad M, Donoho D. From sparse solutions of systems of equations to sparse modeling of signals and images. SIAM Rev, 2009, 51: 34–81
Candès E, Romberg J, Tao T. Stable signal recovery from incomplete and inaccurate measurements. Comm Pure Appl Math, 2006, 59: 1207–1223
Candès E, Tao T. Decoding by linear programming. IEEE Trans Inform Theory, 2005, 51: 4203–4215
Candès E, Romberg J, Tao T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans Inform Theory, 2006, 52: 489–509
Candès E, Wakin M, Boyd S. Enhancing sparsity by reweighted ℓ 1 minimization. J Fourier Anal Appl, 2008, 14: 877–905
Cohen A, Dahmen W, Devore R. Compressive sensing and best k-term approximation. J Amer Math Soc, 2009, 22: 211–231
Dantzig G. Linear Programming and Extensions. Princeton: Princeton University Press, 1963
Davenport M, Plan Y, Berg E van den, et al. 1-Bit matrix completion. Inform Inference, 2014, 3: 189–223
Donoho D. Compressed sensing. IEEE Trans Inform Theory, 2006, 52: 1289–1306
Donoho D, Elad M. Optimally sparse representation in general (nonorthogonal) dictionaries via ℓ 1 minimization. Proc Natl Acad Sci USA, 2003, 100: 2197–2202
Foucart S, Rauhut H. A Mathematical Introduction to Compressive Sensing. New York: Springer, 2013
Fuchs J. On sparse representations in arbitrary redundant bases. IEEE Trans Inform Theory, 2004, 50: 1341–1344
Goldman A J, Tucker A W. Theory of linear programming. In: Linear Inequalities and Related Systems. Princeton: Princeton University Press, 1956, 53–97
Gopi S, Netrapalli P, Jain P, et al. One-bit compressed sensing: Provable support and vector recovery. J Mach Learn Res, 2013, 3: 154–162
Gupta A, Nowak A, Recht B. Sample complexity for 1-bit compressed sensing and sparse classification. In: 2010 IEEE International Symposium on Information Theory. New York: IEEE, 2010, 1553–1557
Jacques L, Laska J, Boufounos P, et al. Robust 1-bit compressive sensing via binary stable embeddings of sparse vectors. IEEE Trans Inform Theory, 2013, 59: 2082–2102
Kamilov U, Bourquard A, Amini A, et al. One-bit measurements with adaptive thresholds. IEEE Signal Process Lett, 2012, 19: 607–610
Laska J. Regime change: Sampling rate vs bit-depth in compressive sensing. PhD thesis. Houston: Rice University, 2011
Laska J, Baraniuk R. Regime change: Bit-depth versus measurement-rate in compressive sensing. IEEE Trans Signal Process, 2012, 60: 3496–3505
Laska J, Wen Z, Yin W, et al. Trust, but verify: Fast and accurate signal recovery from 1-bit compressive measurements. IEEE Trans Signal Process, 2011, 59: 5289–5301
Le B, Rondeau T, Reed J, et al. Analog-to-digital converters. IEEE Signal Process Mag, 2005, 22: 69–77
Movahed A, Panahi A, Durisi G. A robust RFPI-based 1-bit compressive sensing reconstruction algorithm. In: Information Theory Workshop. New York: IEEE, 2012, 567–571
Plan Y, Vershynin R. One-bit compressed sensing by linear programming. Comm Pure Appl Math, 2013, 66: 1275–1297
Plan Y, Vershynin R. Robust 1-bit compressed sensing and sparse logistic regression: A convex programming approach. IEEE Trans Inform Theory, 2013, 59: 482–494
Plumbley M. On polar polytopes and the recovery of sparse representations. IEEE Trans Inform Theory, 2007, 53: 3188–3195
Shen L, Suter B. Blind one-bit compressive sampling. ArXiv:1302.1419, 2013
Sun J, Goyal V. Quantization for compressed sensing reconstruction. https://hal.archives-ouvertes.fr/hal-00452256/, 2009
Tillmann A, Pfetsch M. The computational complexity of the restricted isometry property, the nullspace property, and related concepts in compressed sensing. IEEE Trans Inform Theory, 2014, 60: 1248–1259
Tropp J. Greed is good: Algorithmic results for sparse approximation. IEEE Trans Inform Theory, 2004, 50: 2231–2242
Walden R. Analog-to-digital converter survey and analysis. IEEE J Sel Areas Commun, 199, 17: 539–550
Yan M, Yang Y, Osher S. Robust 1-bit compressive sensing using adaptive outlier pursuit. IEEE Trans Signal Process, 2012, 60: 3868–3875
Zhang Y. Theory of compressive sensing via ℓ 1-minimization: A non-RIP analysis and extensions. J Oper Res Soc China, 2013, 1: 79–105
Zhao Y B. RSP-based analysis for sparsest and least ℓ 1-norm solutions to underdetermined linear systems. IEEE Trans Signal Process, 2013, 61: 5777–5788
Zhao Y B. Equivalence and strong equivalence between the sparsest and least ℓ 1-norm nonnegative solutions of linear systems and their applications. J Oper Res Soc China, 2014, 2: 171–193
Zhao Y B, Kočvara M. A new computational method for the sparsest solution to systems of linear equations. SIAM J Optim, 2015, 25: 1110–1134
Zhao Y B, Li D. Reweighted ℓ 1-minimization for sparse solutions to underdetermined linear systems. SIAM J Optim, 2012, 22: 1065–1088
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Zhao, Y., Xu, C. 1-Bit compressive sensing: Reformulation and RRSP-based sign recovery theory. Sci. China Math. 59, 2049–2074 (2016). https://doi.org/10.1007/s11425-016-5153-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11425-016-5153-2
Keywords
- 1-bit compressive sensing
- restricted range space property
- 1-bit basis pursuit
- linear program
- ℓ 0-minimization
- sparse signal recovery