Transient-State Analytical Solution for Groundwater Recharge in Triangular-Shaped Aquifers Using the Concept of Expanded Domain

Abstract

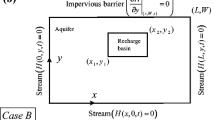
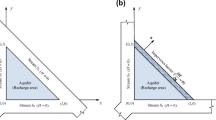
The purpose of this work is to present analytical solution for linearized Boussinesq equation in triangular-shaped aquifers in response to transient recharge from an overlaying basin. Four different configurations of hydrogeological boundary conditions (constant-head and no-flow) are considered. At first, the solutions for the rectangular-shaped aquifers are obtained through the well known image well theory. Then, the concept of expanded domain is utilized to arrive at the solution for the intended triangular domain. The resulting point-recharge solution (Green’s function) facilitates treating any arbitrary shaped recharge basin subjected to spatiotemporal varying recharge. Few examples describing the nature of transient recharge in triangular-shaped aquifers are presented. The investigation of equipotential contour lines and velocity vector fields confirms the validity of the method adopted here. The computed mound profiles are in favourably well agreement with the numerical results obtained by finite element method. Stream flow rates due to recharging are also computed for a single case. Overall, the closed form solutions provide an effective tool in order to conduct sensitivity analysis on various hydrogeological parameters that affect the formation of groundwater mound in triangular-shaped aquifers.

Appendix A

Referring to Fig. 13, the periodic well pattern has the same periodicities of 4L along both coordinate axes with a building block containing 32 point-wells. In addition, the well pattern possesses odd-symmetry about x-axis and even-symmetry about y-axis. This allows a typical point-well to be expressed by double Fourier series as follows:

Fig. 13

Periodic well pattern for Case iii. The building block indicated by ABCD contains 32 point-wells that repeat with periodicities of 4L along both coordinate axes

$$ \frac{{\varepsilon {R_1}}}{{2{L^2}K}}\sum\limits_{m=0}^{\infty } {\sum\limits_{n=0}^{\infty } {{\mu_{mn }}\cos \left( {\frac{{m\pi x}}{2L }} \right)\sin \left( {\frac{{n\pi y}}{2L }} \right)\cos \left( {\frac{{m\pi {x_i}}}{2L }} \right)\sin \left( {\frac{{n\pi {y_i}}}{2L }} \right)} } $$

(A-1)

with (x _i , y _i ) being the position of a typical point-well. Here, ε = +1 and ε = −1 identify the recharge and discharge well, respectively, also

$$ {\mu_{mn }}=\left\{ {\begin{array}{*{20}c} 0 & {\mathrm{for}} & {m\geq 0,\,\,n=0} \\ {\frac{1}{2}} & {\mathrm{for}} & {n>0,\ m=0\ } \\ 1 & {\mathrm{for}} & {m>0,\ n>0} \\ \end{array}} \right. $$

(A-2)

The coordinate system has its origin at the lower left corner of the aquifer. Evaluating Eq. (A-1) for each individual well (i = 0,1,…,31) and adding the resulting expressions together after some algebraic manipulations gives:

$$ \frac{{2R_{1} }} {{L^{2} K}}{\sum\limits_{m = 0}^\infty {{\sum\limits_{n = 0}^\infty {\mu _{{mn}} } }} }{\left[ {{\left( {1 - {\left( { - 1} \right)}^{m} } \right)}{\left( {1 - {\left( { - 1} \right)}^{n} } \right)}} \right]}\cos {\left( {\frac{{m\pi x}} {{2L}}} \right)}\sin {\left( {\frac{{n\pi y}} {{2L}}} \right)} \times {\left\{ {\cos {\left( {\frac{{m\pi x_{0} }} {{2L}}} \right)}\sin {\left( {\frac{{n\pi y_{0} }} {{2L}}} \right)} + {\left( { - 1} \right)}^{{\frac{{m + n}} {2}}} \cos {\left( {\frac{{n\pi x_{0} }} {{2L}}} \right)}\sin {\left( {\frac{{m\pi y_{0} }} {{2L}}} \right)}} \right\}} $$

(A-3)

In deriving Eq. (A-3) some trigonometric identities such as $\sin \left( {{{{m\pi }} \left/ {2} \right.}} \right)\sin \left( {{{{n\pi }} \left/ {2} \right.}} \right)=\left( {{-1 \left/ {4} \right.}} \right)\left[ {\left( {1-{{{\left( {-1} \right)}}^m}} \right)\left( {1-{{{\left( {-1} \right)}}^n}} \right)} \right]\times {{\left( {-1} \right)}^{{\frac{m+n }{2}}}}$ were used. Equation (A-3) identically vanishes if m or n is not an odd integer, otherwise, it simplifies to:

$$ \frac{{4{R_1}}}{{{L^2}K}}\sum\limits_{m=1}^{\infty } {\sum\limits_{n=1}^{\infty } {{T_3}\left( {x,y} \right){T_3}\left( {{x_0},{y_0}} \right)} } $$

(A-4)

where T ₃(x, y) is given by Eq. (31) and the summations are taken over odd values of m and n. Similarly, the expression for the Green’s function is simplified to:

$$ G=\frac{4}{{{L^2}K}}\sum\limits_{m=1}^{\infty } {\sum\limits_{n=1}^{\infty } {{T_3}\left( {x,y} \right)\,{T_3}\left( {{x_0},{y_0}} \right)f\left( {{\kappa_{mn }},t} \right)} } $$

(A-5)

repeating the same expression as for Eq. (30).