On a Model for the Prediction of the Friction Coefficient in Mixed Lubrication Based on a Load-Sharing Concept with Measured Surface Roughness

Abstract

A new model was developed for the simulation of the friction coefficient in lubricated sliding line contacts. A half-space-based contact algorithm was linked with a numerical elasto-hydrodynamic lubrication solver using the load-sharing concept. The model was compared with an existing asperity-based friction model for a set of theoretical simulations. Depending on the load and surface roughness, the difference in friction varied up to 32 %. The numerical lubrication model makes it possible to also calculate lightly loaded contacts and can easily be extended to solve transient problems. Experimental validation was performed by measuring the friction coefficient as a function of sliding velocity for the stationary case.

1 Introduction

Friction, lubrication and wear are highly related phenomena. The presence of lubricating oil between contacting surfaces is often beneficial, as it reduces the shear stresses and thereby friction and wear. By contrast, breakdown of the oil film leads to adverse effects. A film failure is associated with surface roughness. In the case of insufficient lubrication, two sliding bodies under normal load come in direct contact first at the highest peaks (asperities), and the lubricant film breakdown is initiated at these spots. Wear is initiated at these contact spots as well. In line with the efforts to reduce energy consumption, significant efforts have been made in the development of friction models. The literature reveals the existence of two general approaches for the calculation of friction in lubricated contacts: rough elasto-hydrodynamic lubrication (EHL) theory-based methods and load-sharing concept models [1, 2]. In the rough EHL approach, the governing lubricant flow and surface deformation equations are solved numerically assuming a rough surface in both the Reynolds equation as well as for the solid deflection. Despite the significant progress achieved in the development of such models [3–6], certain problems still exist in the “thin film lubrication regime,” such as convergence, accuracy and mesh-dependence [7]. The selection of the film breakdown criteria in mixed lubrication models has a significant effect on the calculated friction values. So far, there is no consensus on this topic.

On the other hand, load-sharing models, first introduced by Johnson [8], offer advantages of robustness and a relatively simple methodology for the estimation of friction. In this approach, separate smooth surface lubrication and dry rough contact models are employed which simplifies the problem. Asperity contact conditions are estimated using dry rough surface contact models, such as the Greenwood and Williamson model [9]. The lubrication models apply the EHL theory under the assumption of smooth surfaces [10, 11] and consequently are more robust than the rough EHL algorithms, as they are typically based on function fits. The contact and lubrication models are linked through the proportionality of the loads carried by liquid and surface contacts [8].

Since Johnson introduced the load-sharing concept, a large number of researchers employed this approach for the calculation of the friction coefficient in lubricated contacts, see for example [12–14], and many attempts were undertaken to reduce the assumptions, making the models more widely applicable. Most of the researchers addressed the limitations of using the dry rough contact models. Greenwood and Williamson [9] pioneered with the asperity-based statistical approach for predicting surface contact interaction. The surface was represented as a set of fully elastic, independent, hemispherical asperities with equal radii of curvature with a Gaussian distribution of heights. Zhao et al. [15] extended the theory to the case of elastic/plastic and fully plastic deformation regimes. Arbitrary height distributions and individual radii of curvature were introduced in deterministic models [16, 17]. Mentioned models can be categorized as uncoupled [18], since the real surface roughness is replaced by a set of independent asperities of simplified geometry. An overview of existing contact models can be found in Ref. [19].

Based on the uncoupled approach, a number of researchers developed friction and wear models. Gelinck et al. [20] extended Johnson’s model to calculate friction in all lubrication regimes in line contacts. Akbarzadeh et al. [21] included a thermal reduction in the film thickness and viscosity of the lubricant due to heat generated by both the lubricant and asperities using the statistical approach. The statistical elasto-plastic asperity contact model was utilized by Masjedi et al. [13] along with the numerical solution of EHL equations for smooth surfaces to construct a curve-fit formula of the traction coefficient. Recently, Chang et al. [22] introduced the influence of boundary film tribo-chemistry on the asperity level to account for variation of the shear strength of boundary films.

On the other hand, also coupled models for the solution of dry rough contact problems exist. These models take the measured surface topography as it is and do not require any additional assumptions on the geometry of asperities or their height distribution. Interactions due to deflections are taken into account automatically. In this type of models, the half-space approximation theory is widely used [23]. The solution in this case is obtained numerically [24]. Numerical methods for the solution of dry rough contact problems based on half-space approach were developed by Polonsky [25], Liu [26] and Tian [27].

So far, the load-sharing lubricated friction methodology mostly relied on uncoupled models due to their very limited computational effort. Some estimations state that the assumption of independent asperities employed in such models does not hold when the ratio of the central film thickness to the standard deviation of asperity heights is less than 0.5 [2]. A model based on coupled contact approach was used by Bobach et al. [28] to calculate friction in mixed lubrication. The half-space theory was employed to pre-calculate the dry mean contact pressure as a function of deformed gap height by assuming nominally flat surfaces in contact. And further, it was incorporated into the load-sharing concept to find the fraction of the load carried by solid contacts and lubricant. Multilevel multi-integration was used to facilitate the calculations. A load-sharing concept-based approach which employs the half-space theory was also implemented by Morales-Espejel et al. [29]. They used Hertz’ theory [23] to calculate the average pressure, and the mean film thickness was obtained from “central film thickness formula,” such as the Dowson and Higginson fit [10] be it with the extension of an equivalent roughness using the perturbation method. However, this makes the approach applicable only to highly stationary, loaded cases. This method was further developed in this paper so that it can also be applied for low loads and transient problems.

The increase in computational power and the development of efficient numerical methods made it possible to consider not only coupled contact models, using the half-space theory, but also numerical smooth EHL theory, to tackle mentioned limitations. Therefore, in the current paper, the load-sharing concept-based models are further improved by taking a non-uniform film into account. The model combines the half-space approximation-based dry contact model with a numerical EHL model for smooth surfaces in the scope of the load-sharing concept. It will be demonstrated that the approach can be employed for the calculation of friction, real contact area and contact pressures in lubricated line contacts. Several simulation tests will be performed, and the results will be compared with existing models and experimental data to validate the developed model.

2 Problem Formulation and Solution Methods

As mentioned above, in the load-sharing method, separate dry contact and lubrication models are needed. Therefore, these models are described individually followed by a brief description of the algorithm for the friction calculation. Detailed overviews on algorithms of the load sharing-based models can be found elsewhere [14, 20, 30]. In addition, an artificial rough surface generation technique is discussed in this section.

2.1 Dry, Rough, Half-Space-Based Contact Model

An alternative to the classical description of the surface by means of asperities is the direct use of the (measured) height profile. The half-space approximation can be used to calculate the surface deflection, described by [24]:

$$u\left( {x,y} \right) = \frac{2}{{\pi E^{\prime}}}\iint {\frac{{p\left( {x^{\prime},y^{\prime}} \right)}}{{\sqrt {\left( {x^{\prime} - x} \right)^{2} + \left( {y^{\prime} - y} \right)^{2} } }}{\text{d}}x^{\prime}{\text{d}}y^{\prime}} ,$$

(1)

where $u\left( {x,y} \right)$ is the deflection, $E^{\prime}$ is the composite elastic modulus, and $p\left( {x^{\prime},y^{\prime}} \right)$ is the contact pressure.

If the pressure is known, then the surface deflection can be found according to Eq. (1). In the load-sharing concept, however, the situation is inverse: The deflection is given and the pressure has to be found. For a given separating distance H _S between the surfaces, the deflection is:

$$u\left( {x,y} \right) = \delta \left( {x,y} \right), \forall x,y \in A_{\text{c}}$$

(2)

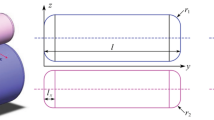
where A _C is the contact area, $z\left( {x,y} \right)$ is the surface roughness profile, $\delta \left( {x,y} \right) = z\left( {x,y} \right) - h_{s} \left( {x,y} \right)$. The contact area A _C is actually not known a priori. The boundary condition reads $p\left( {x,y} \right) \ge 0$ [27]. A schematic diagram of the contact is shown in Fig. 1.

Fig. 1

Schematic diagram of the surfaces in contact

The corresponding system of equations to be solved then reads:

$$\left\{ {\begin{array}{*{20}c} \begin{aligned} u\left( {x,y} \right) = \frac{2}{{\pi E^{\prime}}}\iint {\frac{{p\left( {x^{\prime},y^{\prime}} \right)}}{{\sqrt {\left( {x^{\prime} - x} \right)^{2} + \left( {y^{\prime} - y} \right)^{2} } }}{\text{d}}x^{\prime}{\text{d}}y^{\prime}} \hfill \\ u\left( {x,y} \right) = z\left( {x,y} \right) - h_{s} \left( {x,y} \right), \forall x,y \in A_{\text{c}} \hfill \\ p\left( {x,y} \right) > 0,\forall x,y \in A_{c} \hfill \\ p\left( {x,y} \right) \le P_{u} \hfill \\ \end{aligned} \\ \end{array} } \right.$$

(3)

where P _U is the hardness of the material, beyond which the yielding is initiated. Once the pressure $p\left( {x,y} \right)$ is known, the load carried by surface contacts F _C can be obtained:

$$F_{\text{C}} = \iint {p\left( {x,y} \right){\text{d}}x{\text{d}}y}$$

(4)

In the system (3), $p\left( {x,y} \right)$ and A _C are unknowns, whereas $h_{\text{s}} \left( {x,y} \right)$ is related with the hydrodynamic film thickness, as shown in the next section. The pressure $p\left( {x,y} \right)$ outside of the contact area is zero. The set of equations cannot be solved analytically, and numerical methods have to be used. It also should be noted that the last equation in the system (3) is used to model perfectly plastic behavior of the material [25]. In the case of pure elastic simulations, this condition should be eliminated from the system of the equations.

Computational time necessary for the solution of the system (3) is dominated by the calculation of the integral Eq. (1). This is a convolution integral, and thus, the computational burden can be decreased from $O\left( {N^{2} } \right)$ to the $O\left( {N{ \log }N} \right)$ by discrete fast Fourier transformation technique (DC-FFT) [26]. In this case, Eq. (1) is rewritten in the following form:

$$u\left( {x,y} \right) = K \otimes p$$

(5)

where K is the influence matrix, as described in Appendix 1.

The foundation of the numerical solver of the system (3) is the method developed by Polonsky and Keer [25] and is based on the conjugate gradient method [31]. Their algorithm was developed to solve Eq. (1) for pressure with known applied load. In the current approach, the applied load is unknown. However, there is additional equation for the deflection in the contact area, which is given by the second equation of the system (3). This equation links the dry rough contact solver with the lubrication model through the separating distance $h_{\text{s}} \left( {x,y} \right)$, which is related to the hydrodynamic film. The separating distance must fulfill the condition that the total lubricant volume between the smooth surfaces is equal to that between rough surfaces, as it was defined by Johnson [8]. Therefore, the method of Polonsky and Keer was adapted to solve the considered. The details of the algorithm are given in Appendix 2.

2.2 Numerical Lubrication Model

As mentioned in the introduction, existing numerical methods and increased computational power make it possible to compute the smooth EHL solution in acceptable time. Implementation of the smooth EHL model, rather than a film thickness equation, can extend the applicability of the concept both to a wide range of loads and to transient problems.

The classical system of smooth transient line contact EHL equations is given in the following form:

$$\left\{ \begin{aligned} \frac{\partial }{\partial x}\left( {\frac{{h^{3} }}{12\mu }\frac{{\partial P_{\text{H}} }}{\partial x}} \right) - U\frac{\partial h}{\partial x} - \frac{\partial h}{\partial t} = 0 \hfill \\ F_{\text{H}} = \smallint P_{\text{H}} \left( x \right){\text{d}}x \hfill \\ h\left( x \right) = h_{0} + \frac{{x^{2} }}{2R} - \frac{4}{{\pi E^{\prime}}}\smallint P_{\text{H}} \left( {x^{\prime}} \right){ \ln }\left( {x - x^{\prime}} \right){\text{d}}x^{\prime} \hfill \\ \end{aligned} \right.$$

(6)

where μ is the kinematic viscosity, R is the radius of the cylinder, and H and P _H are unknown film thickness and pressure, respectively. F _H is the load carried by the lubricant film and is considered to be given. $U = \left( {U_{1} + U_{2} } \right)/2$, where U ₁ and U ₂ are the velocities of the moving surfaces. With boundary conditions, this system can be solved numerically to obtain H and P _H. Once this is solved, the bulk deflection of the surfaces due to hydrodynamic pressure P _H is also known and therefore can be taken into account in the calculation of the separation by subtracting it from the initial surface profile $z'\left( {x,y} \right) = z\left( {x,y} \right) - u_{h} \left( {x,y} \right)$, where $u_{h} \left( {x,y} \right)$ is defined in the next paragraph.

In a smooth line contact, the hydrodynamic film thickness $h\left( x \right)$ does not vary in Y direction. However, this does not apply to the roughness $z\left( {x,y} \right)$. It is therefore necessary to have the hydrodynamic solution defined in Y direction as well. This can be accomplished by defining $h\left( {x,y} \right) = h\left( x \right),\forall y$. The same is applied to the deflection due to hydrodynamic pressure: $u_{h} \left( {x,y} \right) = u_{h} \left( x \right), \forall y$ and $u_{h} \left( x \right) = - \frac{4}{{\pi E^{\prime}}}\smallint P_{\text{H}} \left( {x^{\prime}} \right){ \ln }\left( {x - x^{\prime}} \right){\text{d}}x^{\prime}$.

The most widely used numerical solution techniques in EHL are the multigrid method [32–34] and the differential deflection algorithm [35]. The latter approach solves the system in a coupled manner, which makes it robust and fast to converge. This method was used in the current work to calculate the EHL film thickness.

The hydrodynamic film thickness H is used to calculate the separating distance $h_{\text{s}} \left( {x,y} \right)$:

$$h_{\text{s}} \left( {x,y} \right) = h\left( {x,y} \right) - \varepsilon , \forall x,y \in A,$$

(7)

where $\varepsilon$ is a constant and A is the total area. So, the separation $h_{\text{s}} \left( {x,y} \right)$ has the same form as the film thickness (Fig. 10), with the offset value $\varepsilon$ which is found from:

$$\int\limits_{A}^{{}} {h\left( {x,y} \right){\text{d}}A = \iint\limits_{{\widetilde{A}}} {\left( {h_{s} \left( {x,y} \right) - z\left( {x,y} \right) + u\left( {x,y} \right)} \right){\text{d}}\widetilde{A}}} .$$

(8)

where $\widetilde{A}$ is the lubricated area. Equation (8) follows the definition of the separating distance of Johnson [36], but it was modified here to take into account the non-uniform hydrodynamic film and deflection of the surface due to contact and hydrodynamic pressures. It should be mentioned that the total displacement of the surfaces is a sum of the deflection $u\left( {x,y} \right)$ due to contact pressure and the deflection $u_{\text{H}} \left( {x,y} \right)$ due to hydrodynamic pressure. The left-hand side of the equation represents the total volume of the lubricant between smooth surfaces, which is equal to the volume occupied by the pockets formed by the non-contacting part of the surfaces, represented by the right-hand side of this equation. It should be emphasized that the separation value $h_{\text{s}} \left( {x,y} \right)$ depends on the deflection $u\left( {x,y} \right)$. When the surface is loaded, the surface deflects and the volume formed by non-contacting parts between surfaces changes. Therefore, to preserve the lubricant volume according to Eq. (8), the separation values must be changed. On the other hand, as it can be seen from the system (3), the deflection $u\left( {x,y} \right)$ depends on $h_{\text{s}} \left( {x,y} \right)$. Therefore, an equilibrium between $u\left( {x,y} \right)$ and $h_{\text{s}} \left( {x,y} \right)$ must be established. This can be accomplished by iteratively solving the system (3) and Eq. (8), similarly to the algorithm of Morales-Espejel et al. [29]. However, it was found to be time-consuming and a different single-loop approach was developed, which is described in Appendix 2.

2.3 Calculation of the Friction Coefficient

For the calculation of the friction coefficient, the load carried by the surface contacts F _C and the hydrodynamic film F _H are calculated, with the boundary condition that their sum should be equal to the applied load F _T = F _C + F _H. Description of the iterative procedure for finding loads satisfying such a boundary condition can be found in Ref. [14, 37]. The friction coefficient F _C can then be obtained from

$$f_{\text{C}} = \left( {f_{\text{C}}^{b} F_{\text{C}} + F_{\text{sh}} } \right)/F_{\text{T}} ,$$

(9)

where the friction coefficient in boundary lubrication regime F ^B_C has to be obtained experimentally and F _sh is the lubricant shear force, which can be calculated as

$$F_{\text{sh}} = B\int\limits_{{\widetilde{A}}}^{{}} {\tau {\text{d}}x}$$

(10)

where $\tau$ is the shear stress of the lubricant:

$$\tau = \mu \frac{\partial v}{{\partial \widetilde{z}}}$$

(11)

and $v = v\left( {x,\widetilde{z}} \right)$ is the lubricant speed, given by [38]:

$$v\left( {x,\widetilde{z}} \right) = \frac{1}{2\mu }\frac{{\partial P_{\text{H}} }}{\partial x}\left( {\widetilde{z}^{2} - \widetilde{z}h} \right) + \left( {1 - \frac{{\widetilde{z}}}{h}} \right)U_{1} + \frac{{\widetilde{z}}}{h}U_{2}$$

(12)

The shear stress was calculated on the upper surface $\left( {\widetilde{z} = h} \right)$. For the calculation of the pressure–viscosity dependency, the Roelands [38] equation was used.

2.4 Generation of Surface Roughness

To illustrate the performance of the model, rough surfaces with different properties were created digitally, using an approach based on Fourier analysis from Hu [39]. The simulation allows variation of two major parameters, i.e., standard deviation of the surface heights σ and the autocorrelation length L. Examples of generated surfaces are shown in Fig. 2. It is clear that with the increase in the autocorrelation length, the surface roughness becomes smoother in the sense that the curvature of peaks increases and that transitions from one peak to another become less abrupt. This parameter can therefore be used as a rough indicator for the characteristic distance between asperities, as well as the sharpness of surface features.

Fig. 2

Comparison of surfaces with different autocorrelation length. Left L = 34 μm, right L = 57 μm

3 Results and Discussion

The model was employed for the calculation of friction coefficients in stationary lubricated contacts. A set of simulations was performed to validate and explore the behavior of the developed model.

3.1 Artificial Surface Simulation Results

For the first simulation case, surfaces consisting of uniformly distributed spherical asperities of equal radius of curvature (30 μm) and height (500 nm) were used, see Fig. 3. Computational grid size contained $N_{x} \times N_{y} = 2000 \times 2000$ data points with the horizontal spacing A _X = A _Y = 115 nm. The distance λ between the asperities was varied: 14, 20, 30 and 40 μm. The separating distance H _S was considered to be constant throughout the contact, so the nominally flat surfaces in contact were assumed. In the load-sharing concept, the load carried by asperities is of interest, as it determines the fraction of the dry and hydrodynamic friction in the total friction coefficient. This was further explored. When the mentioned surface is loaded against a flat and the half-space theory is applied, a boundary effect rises. As the asperities interact, the inner asperities are influenced by pressures developed on the surrounding asperities from all directions; however, boundary asperities are influenced only from the inner parts of the surface. Hence, to study the interaction effect, it is necessary to exclude the mentioned effect by setting periodic boundary conditions. The considered surface is shown in Fig. 3.

Fig. 3

Uniform surface profile, λ = 20 μm

According to the left picture in Fig. 4, the distance between the asperities does not influence the load carried by a single asperity in the deterministic model. This is as expected since the asperities are assumed to deform independently according to Hertz’ theory. However, this does not hold for the half-space model. The right picture of Fig. 4 shows that for a fixed separation level, the load carried by the asperity decreases with decreasing distance between the asperities. This is caused by the increase in the interaction between the asperities, as the pressures developed at single asperities deflect the whole surface. The increase in the distance between asperities moves the load curves obtained by the half-space model toward the deterministic solution due to the decreasing asperity interaction.

Fig. 4

Load as a function of the separation for two models varying the distance between the asperities. Left—deterministic, right—half-space

Generally, the friction in the fluid film is smaller than the friction in the contacting fraction of the surface (where the load is carried by asperities). Following the load-sharing concept, the friction will be smaller if the ratio of load carried by the fluid film and load carried by the asperities increases.

This leads to the following conclusion: The friction values obtained using the half-space approximation will in general be lower or equal to those calculated by the deterministic asperity-based approach.

As a next step, more complex surfaces generated digitally were analyzed. The autocorrelation length L was varied to explore the differences between deterministic asperity-based and half-space based models. In this set of simulations, the film thickness (and consequently, separating distance) was considered constant in the contact area in the new model as it is done in the deterministic approach. This makes it possible to compare the two models. After all, in this case, observed differences between calculated friction values will originate from the difference in the contact models. Periodic boundary conditions were used in the simulations.

Example friction curves are shown in Fig. 5. There is a clear difference between the frictional values calculated with both models. The maximum deviation is observed at approximately 0.1 m/s. This can be explained by means of the load-sharing concept. In the boundary lubrication regime, which corresponds to low velocities, the load carried by the film is small. Since the coefficient of friction in boundary lubrication is pre-defined, both models will give similar results. With the increase in the velocity, the load carried by the film increases and the load carried by the asperities decreases. Correspondingly, in the half-space approach, the asperities will carry less load while the same separation is imposed compared to the deterministic model, and thus, the lubricant has to carry a larger fraction of the total load. Therefore, the friction coefficient is lower in the half-space approach. With a further increase in the sliding velocity, the friction developed by the film starts to dominate the total friction coefficient, and the influence of the direct contact between asperities diminishes. Hence, the difference between deterministic and half-space approaches becomes smaller as both models use the same EHL model. Finally, in the full film regime, there is no asperity contact, and thus the friction coefficients will match.

Fig. 5

Friction curves. Left L = 34 μm

In order to further explore the behavior of the half-space approach and quantify its deviation from the deterministic model, the maximum relative difference was introduced:

$$d = \frac{{{ \hbox{max} }\left| {f_{d} - f_{c} } \right|}}{{f_{d}^{m} }} \times 100\,\% ,$$

(13)

where F _D and F _C are the friction coefficient obtained by the deterministic and new model, respectively. The F ^M_D is the deterministic friction coefficient at the place where the difference $\left| {f_{\text{d}} - f_{\text{c}} } \right|$ has reached a maximum.

The friction curves were calculated for two surfaces with equal standard deviation of heights (240 μm), but with autocorrelation lengths L = 34 μm and L = 57 μm. The maximum relative difference D was then calculated as a function of load and autocorrelation length, Fig. 6. Computational grid size contained $N_{\text{x}} \times N_{\text{y}} = 816 \times 816$ data points with the horizontal spacing A _X  = A _Y  = 2 μm. First of all, it is clear that the maximum relative difference D can reach almost 32 % at a contact load of 1 GPa, which is considerable. Secondly, the difference depends on the load. Obviously, by increasing the load, more asperities come into contact, increasing the degree of the deformation, and therefore, most likely, the distance between neighboring asperities in contact will decrease. According to previous considerations, this leads to an increase in “neighboring” effect. Finally, there is a clear influence of the autocorrelation length parameter. With the increase in L, the deviation between the models diminishes. As the autocorrelation length roughly characterizes the distance between the surface peaks, such result is in agreement with conclusions obtained earlier for uniformly distributed asperity cases.

Fig. 6

Parameter d as a function of load and autocorrelation length L

3.2 Comparison with Experimental Measurements

Further validation of the new model was accomplished using friction measurements in cylinder on disk sliding tests with mineral oil as a lubricant. The viscosity grade of the oil is 150 cSt at 40° C. The tests were performed at room temperature 25° C. Friction curves as a function of sliding velocity were measured for a number of samples and then averaged. A line contact problem was considered with the properties shown in Tables 1 and 2, where B is the contact width and α is the pressure–viscosity coefficient. The nominal contact pressure in this case is 102 MPa. It should be mentioned that since the pressure is not high, the pressure–viscosity coefficient plays a minor role in the lubricant friction. For the simulation, periodic boundary conditions were set in the direction perpendicular to sliding only, since in this case, a cylindrical geometry is considered.

Table 1 Material properties

Table 2 Oil properties

The surface roughness is shown in Fig. 7. As it can be seen, the surface is quite smooth. Computational grid size of the contact model contained $N_{x} \times N_{y} = 200 \times 200$ data points with the horizontal spacing A _X  = A _Y  = 0.45 μm. Computational grid size of the hydrodynamic solver contained N ^H = 2000 data points with a^h = 0.8 μm. The hydrodynamic grid was taken to be considerably larger than the dry contact area in order to exclude possible starvation effects. It should be noted that since the hydrodynamic and contact models grids are different, the former is interpolated to the contact grid.

Fig. 7

Surface roughness profile, m. Standard deviation σ = 100 nm

Simulated friction curves along with experimental measurement data are shown in Fig. 8. Three simulation curves are shown. The most deviating curve corresponds to fully elastic, deterministic, asperity-based contact model linked with numerical shear stress calculation (thus, in full film regime, measurement and simulation match). The closest to experimental data simulation curves were obtained using the discussed half-space-based models with fully elastic and elastic, fully plastic, surface deformation regimes.

Fig. 8

Comparison of the developed model with experimental data and elastic deterministic model

As it can be seen, the half-space-based models are in a good agreement with experimental data. Slight effect of plastic regime also can be noted. Assumption of the fully elastic deformation leads to the same effect as the assumption of independent asperity deformation—it overestimates the loads carried by contact spots and as a result overestimates the friction coefficient. Due to smooth surface and light load, the effect of plastic deformation is limited.

From the width of the measurement 90 % confidence interval, it can be noticed that the variance of the experimental data is almost negligible in the full film regime, i.e., the right side of the friction curve, and becomes larger toward the boundary lubrication, i.e., the left side. This variation is caused by the difference in roughness profiles of the samples. This difference does not play any role in the full film regime, as the surfaces are completely separated by the lubricant film, but is influential in the boundary lubrication.

The dry contact pressure profile developed in the boundary lubrication regime is shown in Fig. 9. It can be noticed that the pressure profile reaches the hardness values at some contact spots. At these areas, the surfaces deform in the fully plastic regime, which is modeled using a cutoff pressure in the CGM algorithm as is discussed [25]. The total number of asperities in contact is low, since the applied load is low.

Fig. 9

Pressure developed at asperity contacts, elastic, fully plastic case. Boundary lubrication regime, U = 10 e⁻³ m/s, F_c = 5.275 N, F_H = 0.225 N

Further, in Fig. 10, the cross sections of the film thickness, separation and the surface are shown in boundary lubrication and full film regimes, corresponding to the speed U = 0.001 m/s and U = 0.3 m/s, respectively. Clearly, in boundary lubrication, the separation cannot prevent the surfaces from contacting, as shown in Fig. 10a. The contact spots generate high total friction coefficient, as shown in Fig. 8. On the other hand, in the full film regime, Fig. 10b, there is enough lubricant film to completely separate surfaces from contact. Under these conditions, the friction is generated only by the shear of the lubricant film and therefore is low compared to the boundary value, see Fig. 8.

Fig. 10

Cross section. Surface, separation and film thicknesses in boundary (a U = 10 e⁻³ m/s, F_c = 5.275 N, F_H = 0.225 N) and in full film regimes (b U = 0.3 m/s, F_c = 0 N, F_H = 5.5 N

4 Conclusion

A robust and fast numerical algorithm for the calculation of the friction coefficient in lubricated line contact problems was developed based on a half-space approximation approach and numerical smooth EHL theory using the load-sharing concept. This model does not require additional assumptions on the geometry of asperities and takes into account their interaction during deformation. The use of a numerical smooth EHL solver, rather than a film thickness formula, makes it possible to solve lightly loaded and transient problems in the future.

The model was validated using an existing deterministic asperity-based friction model, artificial surface simulation tests and experimental measurements. The results show that the independent asperity deformation assumption employed in many existing friction models can cause a deviation in predicted friction up to 32 %. This deviation depends on the applied load and surface roughness characteristics. It leads to an overestimation of the loads carried by the asperities, resulting in an overestimation of the friction coefficient. Comparison of the simulation data with experimental measurements showed a good agreement and illustrates the accuracy of this friction model.

Appendices

Appendix 1

After discretization of the governing equations on a numerical grid Ω, the influence matrix K is given by a following expression [23]:

$$\begin{aligned} \pi E^{\prime}K_{ij} & = \left( {x_{i} + a_{x} } \right){ \ln }\left[ {\frac{{\left( {y_{j} + a_{y} } \right) + \left\{ {\left( {y_{j} + a_{y} } \right)^{2} + \left( {x_{i} + a_{x} } \right)^{2} } \right\}^{\frac{1}{2}} }}{{\left( {y_{j} - a_{y} } \right) + \left\{ {\left( {y_{j} - a_{y} } \right)^{2} + \left( {x_{i} + a_{x} } \right)^{2} } \right\}^{\frac{1}{2}} }}} \right] \\ & \quad + \left( {y_{j} + a_{y} } \right){ \ln }\left[ {\frac{{\left( {x_{i} + a_{x} } \right) + \left\{ {\left( {y_{j} + a_{y} } \right)^{2} + \left( {x_{i} + a_{x} } \right)^{2} } \right\}^{\frac{1}{2}} }}{{\left( {x_{i} - a_{x} } \right) + \left\{ {\left( {y_{j} + a_{y} } \right)^{2} + \left( {x_{i} - a_{x} } \right)^{2} } \right\}^{\frac{1}{2}} }}} \right] \\ & \quad + \left( {x_{i} - a_{x} } \right){ \ln }\left[ {\frac{{\left( {y_{j} - a_{y} } \right) + \left\{ {\left( {y_{j} - a_{y} } \right)^{2} + \left( {x_{i} - a_{x} } \right)^{2} } \right\}^{\frac{1}{2}} }}{{\left( {y_{j} + a_{y} } \right) + \left\{ {\left( {y_{j} + a_{y} } \right)^{2} + \left( {x_{i} - a_{x} } \right)^{2} } \right\}^{\frac{1}{2}} }}} \right] \\ & \quad + \left( {y_{j} - a_{y} } \right){ \ln }\left[ {\frac{{\left( {x_{i} - a_{x} } \right) + \left\{ {\left( {y_{j} - a_{y} } \right)^{2} + \left( {x_{i} - a_{x} } \right)^{2} } \right\}^{\frac{1}{2}} }}{{\left( {x_{i} + a_{x} } \right) + \left\{ {\left( {y_{j} - a_{y} } \right)^{2} + \left( {x_{i} + a_{x} } \right)^{2} } \right\}^{\frac{1}{2}} }}} \right] \\ \end{aligned}$$

where A _X and A _Y are the half mesh size in direction X and Y correspondingly, X _I , $y_{j} \in\Omega$.

Appendix 2

The process starts with the initialization of the pressure $p\left( {x,y} \right)$, which can be arbitrary or obtained from the previous iteration step. The area of contact A _C is then defined as the sum of those areas where $p\left( {x,y} \right) > 0$. The hydrodynamic area is the total area subtracted the contact area $\widetilde{A} = A \cap \overline{A}_{\text{c}}$. The corresponding deflection $u\left( {x,y} \right)$ is found according to Eq. (1) using the DC-FFT technique. The initial separation value H _S is calculated through the Eq. (8). Auxiliary variables G _OLD = 1 and $\delta = 0$ are defined.

Iterations start, and first the gap distribution is obtained:

$$g_{ij} = - u_{ij} + z_{ij} - h_{\text{s}}$$

(14)

This gap is positive in areas of contact and negative in lubricated areas. Note that here U _IJ are positive. For the gap G _IJ , new variable G is introduced:

$$G = \mathop \sum \limits_{{A_{\text{c}} }} g_{ij}^{2}$$

(15)

And a new conjugate direction is computed:

$$t_{ij} = g_{ij} + \delta \left( {G/G_{\text{old}} } \right)t_{ij} , t_{ij} \in A_{\text{c}}$$

$$t_{ij} = 0, t_{ij} \notin A_{\text{c}}$$

(16)

Convolution of the influence matrix and T _IJ is then obtained:

$$r_{ij} = - K \otimes t_{ij} , t_{ij} \in A$$

(17)

Mean value of R _IJ is then adjusted as

$$r_{ij} = r_{ij} - \overline{r} , r_{ij} \in A,\overline{r} = N_{\text{c}}^{ - 1} \mathop \sum \limits_{{r_{kl} \in A_{c} }} r_{kl}$$

(18)

where N _C is the number of points in the contact area A _C. The length of the step in the direction T _IJ is then:

$$\tau = \frac{{\sum g_{ij} t_{ij} }}{{\sum r_{ij} t_{ij} }}, g_{ij} ,r_{ij} ,t_{ij} \in A_{\text{c}}$$

(19)

The pressure is stored as P ^OLD _IJ  = P _IJ and the new pressure profile can be found from:

$$p_{ij} = p_{ij} - \tau t_{ij} , p_{ij} ,t_{ij} \in A_{\text{c}}$$

(20)

The negative values of P _IJ are set to zero. Further, it is necessary to include into consideration the points, where pressure is zero, but surfaces overlap. The fact that they overlap indicates that they are in contact, and thus, the pressure must be positive. The surfaces are overlapping, if G _IJ  > 0. The following area is introduced

$$A_{ol} = \left\{ {A:p_{ij} = 0,g_{ij} > 0} \right\}$$

(21)

If $A_{ol} = \emptyset$, $\delta$ is set to unity; otherwise, it is set to 0. In this area, the pressure is then corrected accordingly as:

$$p_{ij} = p_{ij} - \tau g_{ij} , \{ p_{ij} ,g_{ij} \in A_{ol} \}$$

(22)

The pressure obtained using this equation is always positive as $\tau$ is always negative [25]. After that, the deflection and the new value for separation are calculated according to the first of the Eqs. (3) and (8) correspondingly. The iterations continue until the difference in separation level between two successive iterations is less than the desired value $\varepsilon_{0}$:

$$\varepsilon = \frac{{\left| {h_{\text{s}} - h_{\text{s}}^{\text{old}} } \right|}}{{h_{\text{s}}^{\text{old}} }} \le \varepsilon_{0}$$

(23)

In rough surface contact problems, the plastic limit is usually set as an upper boundary for the pressure, where the material starts yielding. In the described algorithm, it is possible to impose this condition the same way as the condition on the positivity of the contact pressure on each iteration, $p_{ij} \le P_{\text{u}}$, where P _U is the plastic limit.