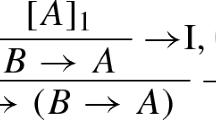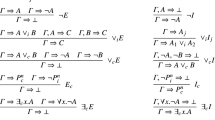Abstract
From the point of view of proof-theoretic semantics, it is argued that the sequent calculus with introduction rules on the assertion and on the assumption side represents deductive reasoning more appropriately than natural deduction. In taking consequence to be conceptually prior to truth, it can cope with non-well-founded phenomena such as contradictory reasoning. The fact that, in its typed variant, the sequent calculus has an explicit and separable substitution schema in form of the cut rule, is seen as a crucial advantage over natural deduction, where substitution is built into the general framework.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper we discuss what it means for the format of deductive reasoning when what we have called the “dogmas of standard semantics” (see Schroeder-Heister 2008; 2011a) are given up. The first and main dogma is the priority of the categorical over the hypothetical. This dogma means that hypothetical concepts are explained in terms of categorical concepts, so that the hypothetical concepts have a derivative status. In standard model-theoretic semantics the categorical concept is that of truth in a model. The hypothetical concept of consequence is then defined by saying that whenever the antecedents of a consequence statement are true, then so is the consequent. By ‘consequence’ I here mean material consequence, not necessarily formal consequence. The latter is obtained from material consequence by abstracting from non-logical features of the propositions involved, which in the model-theoretic case is achieved by quantifying over all models. The dogma of the priority of the categorical over the hypothetical holds for standard proof-theoretic explanations of consequence as well. For example, in Dummett-Prawitz-style proof-theoretic semantics based on a proof-theoretic notion of validity, the validity of assumption-free (or ‘closed’) proofs is defined first, and the validity of hypothetical (or ‘open’) proofs and thus the notion of consequence is defined in terms of that of closed proofs (see Schroeder-Heister 2006).
The second dogma of standard semantics, which is a specialization of the first one, is the transmission view of consequence. In the model-theoretic case it means that consequence can be established by showing that truth (in a model) transmits from the antecedents to the consequent of the consequence claim. In the proof-theoretic case it means that there is a procedure which transforms proofs of the antecedents into a proof of the consequent. There are several variants of the proof-theoretic approach: besides the above mentioned Dummett-Prawitz-style semantics e.g. the BHK-interpretation or Lorenzen’s admissibility interpretation of the logical constants. They all understand this transmission as a constructive procedure, whereas in the classical model-theoretic case it is essentially a metalinguistic universally quantified ‘if … then …’. Together with the transmission view of consequence comes the placeholder view of assumptions, which is the idea that in deductions open assumptions are ‘satisfied’ by proofs of them.
The third dogma is the equivalence of valid consequence and correctness of inference, or at least that valid consequence entails the correctness of inference. Whenever a consequence statement is valid, we can proceed inferentially from its antecedents to its consequent, i.e., a valid consequence licenses a corresponding inference. This is what soundness of inference rules means.
What is common to all these dogmas is that assumptions or hypothetical claims are not given a status in their own right. They are dependent on categorical concepts and their handling. We argue instead for an alternative approach which takes consequence and thus the hypothetical concept first and considers categorical truth to be a limiting case of consequence, namely consequence without assumptions. The formal model of this approach is Gentzen’s sequent calculus, whose semantical significance has not been appropriately acknowledged, contrary to his calculus of natural deduction, which has been the dominant formal model in meaning-theoretical investigations.
The rationale for this different approach is not only the general philosophical consideration of the notion of consequence. The standard approach has certain limits which can be overcome by considering the hypothetical concept. The most fundamental of these limits is the well-foundedness assumption, which means that the categorical concepts (truth, canonical provability) are defined in a strictly well-founded way, leaving no space for issues such as circularity or infinitely descending definitional chains. Non-well-founded phenomena are apparently present, for example, in the paradoxes, and an approach to reasoning should be able to deal with them. The approach based on hypothetical consequence as the primary concept is versatile enough to achieve this. It covers the well-founded case, but still allows one to deal with irreducibly paradoxical statements such as self-contradiction.
2 Definitional Freedom
The claim of definitional freedom, and the comparison with recursive function theory is due to Hallnäs (1991, 2006).
One can avoid non-well-foundedness by requiring that, when we define something, this must be carried out in a stepwise, well-founded fashion. However, this is not as easy to achieve as it may appear at first glance, since a definition does not always exhibit whether it is well-founded or not. For example, if we deal with clausal definitions as in logic programming, which are similar to inductive definitions, it is not even always decidable whether a particular substitution instance of a defined proposition has a well-founded definitional chain. This corresponds to the fact well-known from recursive function theory that being total is not generally a decidable property of a partial recursive function. One would nonetheless, at least nowadays, in the age of computer science, admit arbitrary partial recursive functions as well-defined entities, and leave it to be a matter of (mathematical) fact whether a function is defined (has a value) for a particular argument or not.
One is used to well-foundedness from the case of the standard logical constants, when proof-theoretic validity is defined. However, not everything for which a definition can be written down is ‘well-behaved’ in this sense, and there is no reason to confine oneself to such cases. There is a tendency in philosophical semantics, in particular in its proof-theoretic branch, to concentrate on logical constants, logical consequence, and logicality in general. Nevertheless, there are concepts more general than logical ones, and the restriction to logical concepts can prevent one from getting on overview of what can be defined (proof-theoretically or otherwise).
We strongly propose definitional freedom in the sense that there should be one or several formats for definitions, but within this format one should be free. Whether a certain definition is well-behaved is a matter of (mathematical) ‘observation’, and not something to be guaranteed from the very beginning.
3 Type Systems for Clausal Definitions
We use clausal definitions as in logic programming, where an atom A is defined in terms of certain conditions Γ1, …, Γ n understood as alternative ways of introducing A:
This list of clauses is called the definition of A, and a definition (simpliciter) is a collection of such lists for various defined atoms A. Thus a definition is exactly like a logic program, with the exception that we do not restrict the conditions (‘bodies’ in logic programming) to lists of atoms, perhaps with negations. In principle we allow for any logical composition, but we leave this point open here. Obviously, clausal definitions can also be viewed as inductive definitions, looked upon as rule systems (see Aczel 1977; Denecker et al. 2001). A definition is put into action by certain inference schemata. In which way this is done depends on the reasoning format chosen. In a natural deduction format, we define introduction and elimination rules for atoms as follows:
The introduction rules express the reasoning along definitional clauses. The elimination rule corresponds to what is known as generalized elimination rules in natural deduction. Within the general definitional setting they are very powerful and go beyond what is available, for example, in standard accounts of logic programming. They express the principle of definitional reflection, which is a sort of inversion principle according to which everything that can be inferred from each defining condition of A can be inferred from A itself. It develops its full power when clauses contain variables and are not just of the propositional kind dealt with here. When we speak of ‘atoms’ which are defined, and for which introduction and elimination rules are given, we mean atoms in the sense of logic programming, i.e., the entities to be defined, not atoms in the logical sense. Therefore logically compound expressions, for which a definition is given, would be atoms in our sense as well. (For further details see Hallnäs 1991; Hallnäs and Schroeder-Heister 1990/1991.)
In the present context it is more instructive and useful to present the inference rules as a type system (see Hallnäs 1991):
Here the c i are constructors for canonical terms of type A, the dot denotes a binding operation, and D is a selector with the following reduction (or equality) principle:
It says that if t reduces to canonical form c i s, then s can be substituted for the variable x i in the ith minor premiss of (1), yielding a term t i [x i /s] of type C. For simplicity we assume that the Γ i are single types (otherwise, t : Γ i would have to be understood as representing lists of typing judgements). If there is just a single clause for A, then no selector is needed. Instead of the rules
and the reduction principle
we can equivalently use a direct elimination rule, yielding
with the reduction principle
Here c′ is the destructor that annihilates c. One should remember our presupposition that Γ is a single type—a strong simplification, which is however sufficient for the present purposes. (Already in the case of standard conjunction there would be a pair of types giving rise to two direct elimination rules.)
In a sequent-style reasoning format there are right introduction and left introduction rules for the defined atom A:
If Γ i consists of more than one formula, Δ ⊢ Γ i is understood as a list of sequents (we are not considering multiple-formulae succedents here). In a type system, Δ is a list of declarations of the form y : B, and we have the following rules:
with the reduction principle (2).
In the case of a single clause for A, we can again formulate the rules in the simpler direct way as follows:
with the reduction principle (4).
We also need a term-annotated version of the rule of cut, which is a substitution rule:
4 Self-Contradiction
The consideration of paradoxes in the clausal framework and the self-contradictory definition of R as a standard example and test case in a theory of definitional reasoning goes back to Hallnäs (1991, see also Hallnäs and Schroeder-Heister 1990/1991).
A most elementary circular definition, which immediately leads to contradiction, is the definition of an atom R in terms of its own negation \(\neg R. \) We understand \(\neg R\) in the intuitionistic way as implying absurdity: R → ⊥. In this way we can distinguish between a contradiction consisting of the pair R and \(\neg R, \) and absurdity ⊥. The letter R should remind one of the Russell paradox. The definition of the Russell set within naive set theory can be viewed as a sophisticated way of defining something in terms of its own negation. Using our definitional framework we do not need to introduce any set-theoretic notion.Footnote 3
For implication we need typed introduction and elimination rules for the natural deduction framework, as well as right and left introduction rules for the sequent framework. For natural deduction these are the common ones of lambda abstraction and term application:
together with the reduction principle of application reduction, which is the same as β-contraction:
The corresponding rules for the sequent calculus are as follows:
together with App-reduction (8). The left introduction rule corresponds to modus ponens, but differs from Gentzen’s implication left rule, from which it can be derived in two steps. Here we use it for convenience and abbreviation. We do not discuss the point that it might be preferable to Gentzen’s rule anyway (see Schroeder-Heister 2011b).
Now we define the self-contradictory R as follows:
If we denote the constructor for R by r, then from (1) and (5) we obtain the following typing rules in the natural deduction and sequent systems:
and
together with the reduction principle
Instead of using (9) or (10) to derive a contradiction, we use the simpler forms corresponding to (3) and (6)
and
together with the reduction principle
In the natural deduction system we then obtain a typed proof of absurdity \(\bot\) as follows:

The term obtained for absurdity is not normalizable, as seen from the following reduction sequence which loops:
This witnesses the fact that the given derivation, which without terms can be written as follows,

is not normalizable. It corresponds to what was first observed by Prawitz (1965, Appendix B) in the context of a natural deduction formulation for naive set theory.
In the sequent calculus, for the derivation of the absurdity sequent \(\vdash \bot\) the rule of cut is required in the last step:

Annotated with terms, this derivation looks as follows:

The term generated for absurdity is essentially the same as the one generated in the natural deduction variant. More precisely, it is the second line of the looping reduction (12), so we have again a non-normalizable term. Here it reflects the fact that there is no cut-free proof of absurdity. If we carry out the standard reductions for eliminating cuts, we obtain again a non-terminating sequence of reduction steps. We leave the details to the reader.Footnote 4
5 Absurdity in Natural-Deduction-Style Reasoning
Our natural-deduction-style type system attempted to be a framework for reasoning with respect to any definition, including self-contradicting ones. It is based on the idea that with a definition a corresponding pair of introduction and elimination rules is associated, according to which we can proceed in a natural-deduction manner starting from assumptions (and also discharging assumptions when permitted by the rules). This is a concept according to which a valid proof is a proof composed of introduction and elimination inferences of the justified kind. So we do not, as in Dummett-Prawitz-style semantics, define the validity of proofs first, and then the validity of rules as respecting the validity of proofs. Dummett’s and Prawitz’s idea of putting proofs first is intimately linked to the dogma that closed proofs are primary to open ones, i.e., the categorical is primary to the hypothetical. It is also linked to the well-foundedness assumption: In Dummett and Prawitz, the validity of (canonical) closed proofs is defined in terms of its closed subproofs of lower complexity, something that breaks down in the case of our definition of R. Since in our approach rules are conceptually prior to proofs, hypothetical proofs are simply validated by rules leading from assumptions to conclusion, and no longer by the transmission of valid categorical proofs.
This does not mean that we are just laying down a formal system, as might be raised as an objection. The introduction and elimination rules we are proposing are not arbitrary, but are justified as rules putting definitional clauses into action. They complement one another in the sense of an inversion principle, making the eliminations inverses of the introductions. However, this complementation is not based on global ideas of reducibility of proofs, but is a local principle, which only assumes that an atom is defined by certain conditions. It does not assume that these conditions are of lower complexity than the atom. For more details relating this approach to Dummett-Prawitz-style semantics see Schroeder-Heister (2011c).
Given the definition \({{\mathbb{D}}_R}\) of R this means that there is a derivation of absurdity \(\bot\) which has the feature that it is not normalizable, witnessed by the fact that in typed form we derive \(t : \bot\) with non-normalizable t. Semantically, the term t represents the knowledge one has gained by proving \(t : \bot. \) Distinguishing in the spirit of Dummett-Prawitz semantics between indirect and direct knowledge, one might say that a term in normal form represents direct knowledge, whereas a non-normal term represents indirect knowledge. According to this type of semantics, the distinction between indirect and direct knowledge is crucial, together with the principle that indirect knowledge can always be transferred into direct knowledge (called the ‘fundamental assumption’ by Dummett 1991, Chap. 12). In fact, the validity of indirect knowledge is defined by reference to the direct knowledge it can be reduced to.
In our case this could lead to the suggestion that the derivation of \(t : \bot\) shows that absurdity can be proved, but only in a sense of delivering indirect knowledge. Referring to the non-normalizability of t, we could put forward the idea of ‘ultimately indirect’ knowledge, i.e., knowledge that cannot be ‘directified’. We could say that a derivation of absurdity is possible in our generalized definitional framework, but only by yielding ‘ultimately indirect’ evidence of it. In general we would then say that certain definitions—those which are ‘well-behaved’—always produce direct, i.e. ‘first-class’ knowledge, whereas others like that of R may produce only ‘second-class knowledge’ that cannot be ‘upgraded’ to ‘first-class knowledge’ by means of term reduction. If one wanted to give this idea a very broad philosophical perspective, one could put it in relation to the discussion of theoretical terms in philosophy of science and associate with it the fact that theoretical terms are only indirectly linked with observational ones. This would give definitions such as \({{\mathbb{D}}_R}\) a Quinean aspect.
However, it is not obvious what this non-directifiable indirect knowledge actually might be. Should there be any knowledge of absurdity at all? Note that absurdity does not just mean contradiction. In the last step of the proof of absurdity we proceed from \(\neg R\) and R by modus ponens to absurdity, from which we could proceed to any other proposition. We are not proposing a paraconsistent system, but a system, in which everything can be proved, though not in a ‘first-class’ way. The fact that in a proof of \(t : \bot\) the term t is not normalizable, should perhaps not be given too much weight, since normally one would argue that by simply omitting the term information in a proof, and keeping only the types, one would still be left with a proof, though with a proof carrying less information. The idea of distinguishing between first-class and second-class proofs of the same proposition, and giving only the first-class ones real epistemic significance is problematic. We want to have no proof of absurdity at all, not a second-class proof of absurdity that lacks certain global properties such as normalizability.
6 Absurdity in Sequent-Style Reasoning
In the sequent-style framework we have obtained a derivation of \(\vdash t:\bot\) with a non-normalizable t by using the cut rule. However, the cut rule is not a primitive rule of the framework. So we are not entitled to use it, except we have shown beforehand that it is eliminable. For many definitions, this can be achieved, but not for \({{\mathbb{D}}_R. }\) Epistemologically, we do not need to distinguish between first-class and second-class proofs. Instead we can say that, with respect to \({{\mathbb{D}}_R, }\) we have both a proof of \(\vdash R\) and a proof of \(R \vdash \bot, \) but not a proof of \(\vdash \bot. \) In other words, we have proofs of both R and its negation, but not a proof of absurdity, which means that our system is paraconsistent. This sort of paraconsistency gives us the possibility to use definitions like \({{\mathbb{D}}_R}\) without devastating consequences. The principle of definitional freedom need not be given up. That we generate a contradiction if we define R in a contradictory way, is not implausible. We do not generate absurdity out of this definition, not even some sort of ‘second-class’ absurdity.
This result is obtained by a particular feature of sequent-style reasoning. The principle of cut is separated as a special structural rule from the framework of the meaning-giving rules. With respect to the meaning-giving rules, nothing prevents us from giving up cut in principle. We thereby depart radically from the fact that consequence entails correct inference, one of the dogmas of standard semantics, which is embodied in the principle of cut. Even if we have established that B follows from A as expressed by the sequent \(A \vdash B, \) this does not necessarily mean that, if we have furthermore established \(\vdash A, \) we can establish \(\vdash B, \) which is a case of cut. This feature: the separation of meaning from transitivity in the sense of cut, is achieved by the institution of left-introduction rules. In the sequent calculus, we introduce assumptions (i.e., propositions in the antecedent of a sequent) not only by trivial initial sequents (which correspond to assumptions in natural deduction), but by explicit assumption-introduction (= left-introduction) rules, which depend on the form of the assumption being introduced. This is the proper way of taking assumptions seriously, a way that overcomes the dogmas of standard semantics. The primary relation is that of consequence as expressed by the sequent sign, and we have rules for assertion (right-rules) as well as rules for assumptions (left-rules) which make up consequence. The fact that one may join two consequence statements according to the transmission view is something that depends on the presupposed definition.
Combining proofs is a matter of a structural rule, namely cut. It is not intertwined with meaning-giving principles. This strongly speaks for the sequent-style approach to reasoning. In our derivation of absurdity in the natural-deduction framework (13)/(11), the problem arises with our last application of modus ponens, which corresponds to the final cut in the sequent-calculus derivation (14)/(15). But we cannot just refrain from using modus ponens in a way in which we can refrain from using cut, as modus ponens is an indispensible meaning-giving principle, whereas cut is not, as the meaning of implication is given by inference principles of its own. Therefore, from a semantical point of view, the parallel between cut elimination and normalization is far from perfect. It makes a crucial difference of whether the usage of a special local rule, namely cut, or the global form of the whole proof, namely normalization, is at stake. This comes to bear when there is no normalization/cut elimination. Then in the sequent calculus the unproblematic part can just be saved by removing the local cut rule, whereas in natural deduction this part is defined by some sophisticated global property (normalizability).
One might, of course, model natural deduction according to the sequent calculus. One possibility would be to use the strategy of generalized elimination inferences which actually makes natural deduction a notational variant of the sequent calculus, yielding something such as ‘bidirectional natural deduction’ (Schroeder-Heister 2009). However, this is not exactly our point here. We are comparing the reasoning formats of natural deduction and the sequent calculus, not ways of simulating one approach within the other.
7 Consequence, Inference, Place-Holders: Intuitive Account
Even if with \({{\mathbb{D}}_R}\) we have an example of a situation in which cut fails, there remains a gap between observing this fact and grasping it intuitively. Suppose we have established \(A \vdash B\) as a consequence (for example, by a derivation in our semantically motivated sequent calculus). Why cannot we later use this consequence to guide an inference from A to B? Why cannot we argue that, because we once have established \(A \vdash B, \) we can savely move from A to B:
Is it not the purpose of establishing consequences that we may use them later on? For example, in the sequent-style framework, it appears absolutely natural to use the consequence \(A \wedge B \vdash A\) in order to proceed by \(\wedge\)-elimination
even without having demonstrated cut elimination. Telling novices in logic that the correctness of this rule has to be formally demonstrated would confuse them.
The reason for this confusion is that the proposition being cut does not stand for the same in both of its positions. In the example, the left occurrence of \(A \wedge B\) stands for something different from its right occurrence. This becomes clear, when the typed version is used:
In the left premiss we have a term t, and in the right premiss we have the variable x, which, by applying cut, becomes substituted. This means that in the case of cut, different terms are involved, together with a substitution operation which is hidden in the non-typed formulation. This hidden substitution operation causes the problem in critical cases. In the last step of our derivation (15) of ⊥, this substitution operation generates a term which is not normalizable.
When we force such a substitution operation to be valid, we end up in paradox. But the question still remains: What is it intuitively that speaks against such a substitution? A tentative answer might be the following. Semantically the variable x in the right sequent of cut (7) is not understood as running over all terms individually, i.e. over all proof terms. Rather, it is understood as an objectual variable running over an arbitrary proof object, abstracting from the specific structure which concrete proofs may have. When performing the substitution in the application of cut, we are substituting this arbitrary object with an individual proof term, which, when embedded into a new context, may behave differently, as this proof term has a specific internal structure. Thus we would invoke the difference made in other areas of logic between objectual quantification, substitutional quantification and arbitrary objects. This idea still needs to be worked out in detail.
8 Closure Under Substitution and the Format of Deductive Reasoning
To repeat, the situation arising with self-contradiction, when treated in a typed system, is that a substitution of a normal term into a normal term results in a non-normal and non-normalizable term. In the sequent calculus, this is due to the application of cut, which is a substitution rule:
Even if s and t are normal, s[x/t] does not need to be normal nor to be normalizable. In natural deduction, a corresponding situation obtains with modus ponens:
Even it s and t are normal, App(s, t) does not need to be normal or normalizable. Our derivations (11) and (15) exemplify this. The advantage of the cut rule is that it makes this substitution operation explicit. By disallowing cut, or by using cut only for definitions, for which we can prove beforehand that cut can be eliminated, we can dispose of the substitution problem.
Now it might be considered a too radical solution: either not to use cut or to prove a cut-elimination theorem beforehand. One might consider instead the idea to use cut whenever it is appropriate, without expecting it to be globally admissible. This could be achieved by means of a side condition, saying that cut can be applied whenever the substitution term generated by cut is normalizable. If we denote the normalizability of a term t by t!, we could then formulate the restricted cut rule as follows:
One must be aware, however, that the side condition goes beyond usual side conditions in proofs as it is not always decidable (depending on the system considered). So one would have to give at least a proof system by means of which s[x/t]! can be established, in such a way that the finitistic concept of ‘proof’ is not given up.
In the natural deduction framework, modus ponens with the corresponding side condition would be
However, this is still not exactly the same situation as in the sequent system. The terms s and t may contain free variables, as the judgements s : A → B and t : A may depend on assumptions. Suppose t, but not s contains the free variable y, and t : A depends on the assumption y : D, so that we have the situation:
Now suppose we have a derivation of t′ : D, and suppose we want, by substituting t′ for y, to combine these two derivations to a derivation of App(s, t[y/t′]) : B, yielding
Then we have to check the validity of the side condition, and of all other side conditions in the derivation above it again, as they are not necessarily closed under substitution (in fact, our self-contradiction example demonstrates this non-closure). In the sequent-calculus framework, in the same situation, we would simply add another cut with an additional side condition:

Here only this additional step needs to be checked, there is no need to rework the whole proof. Footnote 5 In a natural-deduction-style formulation this can be achieved by restricting the combination (substitution) of natural-deduction proofs. However, formulating such restrictions essentially means to give up the natural deduction framework in favor of a sequent-style framework (even though this would be in a natural-deduction-style notation).
The idea of closure under substitution is deeply built into the framework of natural deduction. Imposing side conditions that are not automatically closed under substitution represents a reasoning format that is very difficult to handle. In the sequent calculus, on the contrary, substitution just means applying a rule (namely cut), so substitution is a local principle rather than a global one.
The locality of substitution is what in our eyes ultimately speaks for the sequent format of reasoning. It gives up the dogmas of standard semantics by making the application of consequence, i.e., the transmission of truth, a local issue of rule application rather than a global issue of the reasoning framework.
9 Free Type Theory
We have discussed the possibility of a local rule of cut depending on the side condition that the term being constructed by the substitution operation denotes (is normalizable):
This may suggest the idea of incorporating the side condition, which is an external proviso, into an actual premiss of the cut:
We would obtain some sort of free type theory in which, before generating a term by means of cut, we must first show that it denotes. The type-theoretic view that proofs are objects named by terms would then be combined with the idea of free logic that certain names denote whereas others do not, and for certain inferences and names t occurring in them, there would be the premiss t! expressing that t denotes. The ‘denotes’-claim expressed by the exclamation mark would be an additional form of judgement, for which corresponding proof rules would have to be given. This is a wide field and can here just be proposed as a possible research programme.
Such a programme does not appear totally unreasonable. If we consider type theory in Martin-Löf’s setting, then one of its characteristic features is that the formation rules are not external, but part of the intrinsic framework. Before we can prove t : A, i.e., that t has type A, we must prove first A type, i.e. the fact that A makes sense as a type, according to the proof rules for the ‘type’-judgement, which are the formation rules. Now if there are formation rules for types, one might argue that there should be formation rules for terms as well in the sense that, before one can judge that t is of type A, one must also show that t makes sense as a term, as expressed by the judgement t!. Spelling this out in detail requires reworking the whole framework of type theory and especially its ontology, to adapt it to a definitional framework where no well-foundedness assumptions are made.
In this paper, we have focussed on the impact which the proof-theoretic treatment of the paradoxes has on the appropriate choice of the format of deductive reasoning, and have claimed that a sequent-style format is more appropriate than natural deduction. Given our considerations on normalization and denotation of proof terms, one might try to develop a general theory of sense and denotation of proofs. Some steps in this direction have been taken by Tranchini (2011), who argues that proofs are meaningful (have sense) if they follow a principle of local harmony (which is, for example, not satisfied by Prior’s tonk connective), whereas they denote when in addition they can be reduced to canonical form. Further pursuing this idea will be a natural continuation of what has been presented here.
Notes
Tennant (1982) shows that many well-known paradoxes exhibit a proof-theoretic behavior corresponding to that of R as discussed below: Generating a non-normalizable derivation of absurdity. He therefore sees this feature as the characteristic property of paradoxicality. Also Ekman (1998) argues that the proof-theoretic content of Russell’s paradox can be stated in propositional logic by analyzing the derivation of absurdity from self-contradiction \(R \leftrightarrow \neg R. \)
Note that we have not given a term system which codifies the sequent-style proof directly. In order to achieve that, we would have to present a term reduction system for cut elimination in the style of Dyckhoff (2011) and show that the term constructed for the end-sequent is not normalizable. Our terms, which correspond to those used by Barendregt and Ghilezan (2000), codify the fact that the cut rule is a substitution rule corresponding to the combination of two proofs in natural deduction, which is the semantically significant aspect of it. We also do not discuss the issue of contraction, although contraction is used in (14) and (15) at a crucial place and is very important for the generation of paradoxes.
Note that, as we have assumed that y is not free in s, s[x/t][y/t′] is the same as s[x/t[y/t′]].
References
Aczel P (1977) An introduction to inductive definitions. In: Barwise J (ed) Handbook of mathematical logic. North-Holland, pp 739–782
Barendregt H, Ghilezan S (2000) Lambda terms for natural deduction, sequent calculus and cut elimination. J Funct Program 10:121–134
Denecker M, Bruynooghe M, Marek V (2001) Logic programming revisited: logic programs as inductive definitions. ACM Trans Comput Logic 2:623–654
Dummett M (1991) The logical basis of metaphysics. Duckworth, London
Dyckhoff R (2011) Cut elimination, substitution and normalisation. Manuscript. Abstract available at http://www.univ-nancy2.fr/poincare/documents/CLMPS2011ABSTRACTS/14thCLMPS2011_A3_Dyckhoff.pdf
Ekman J (1998) Propositions in propositional logic provable only by indirect proofs. Math Logic Q 44:69–91
Hallnäs L (1991) Partial inductive definitions. Theor Comput Sci 87:115–142
Hallnäs L (2006) On the proof-theoretic foundation of general definition theory. Synthese 148:589–602
Hallnäs L, Schroeder-Heister P (1990/1991) A proof-theoretic approach to logic programming: I. Clauses as rules. II. Programs as definitions. J Logic Comput 1:261–283, 635–660
Prawitz D (1965) Natural deduction: a proof-theoretical study. Almqvist & Wiksell, Stockholm (Reprinted Mineola NY: Dover Publ., 2006)
Schroeder-Heister P (2006) Validity concepts in proof-theoretic semantics. Synthese 148:525–571
Schroeder-Heister P (2008) Proof-theoretic versus model-theoretic consequence. In: Peliš M (ed) The Logica yearbook 2007. Filosofia, Prague, pp 187–200
Schroeder-Heister P (2009) Sequent calculi and bidirectional natural deduction: on the proper basis of proof-theoretic semantics. In: Peliš M (ed) The Logica yearbook 2008. College Publications, London
Schroeder-Heister P (2011a) The categorical and the hypothetical: a critique of some fundamental assumptions of standard semantics. In: Lindström S, Palmgren E, Westerståhl D (eds) The philosophy of logical consequence and inference, Special issue of Synthese. doi:10.1007/s11229-011-9910-z
Schroeder-Heister P (2011b) Implications-as-rules vs. implications-as-links: an alternative implication-left schema for the sequent calculus. J Philos Logic 40:95–101
Schroeder-Heister P (2011c) Proof-theoretic semantics. In: Zalta E (ed) Stanford encyclopedia of philosophy. Stanford: http://plato.stanford.edu
Tennant N (1982) Proof and paradox. Dialectica 36:265–296
Tranchini L (2011) Proof-theoretic semantics, paradoxes, and the distinction between sense and denotation. Manuscript. Abstract available at http://www.univ-nancy2.fr/poincare/documents/CLMPS2011ABSTRACTS/14thCLMPS2011_A2_Tranchini.pdf
Acknowledgments
In addition to the Pontignano 2010 conference, to which this special issue is dedicated, the ideas contained in this paper have been presented at the Workshops on Logical Consequence (Dubrovnik, May 2010) and Computational Logic (St. Andrews, November 2011) and at seminars in Paris, München, Oxford and Tübingen. I would like to thank all organisers and participants of these events for their helpful comments and suggestions, especially Michael Arndt, Roy Dyckhoff, Volker Halbach, Daniel Isaacson, Hannes Leitgeb, Per Martin-Löf, Thomas Piecha, Dag Prawitz, Stephen Read, Luca Tranchini, Gabriele Usberti, Bartosz Więckowski. This work was supported by the French-German ANR-DFG project “Hypothetical Reasoning—Logical and Semantical Perspectives” (HYPOTHESES) (DFG Schr 275/16-1).
Open Access
This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Schroeder-Heister, P. Proof-Theoretic Semantics, Self-Contradiction, and the Format of Deductive Reasoning. Topoi 31, 77–85 (2012). https://doi.org/10.1007/s11245-012-9119-x
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11245-012-9119-x