Estimation of the Effective Permeability of Heterogeneous Porous Media by Using Percolation Concepts

Abstract

In this paper we present new methods to estimate the effective permeability ($k_\mathrm{eff}$) of heterogeneous porous media with a wide distribution of permeabilities and various underlying structures, using percolation concepts. We first set a threshold permeability ($k_\mathrm{th}$) on the permeability density function and use standard algorithms from percolation theory to check whether the high permeable grid blocks (i.e., those with permeability higher than $k_\mathrm{th}$) with occupied fraction of “p” first forms a cluster connecting two opposite sides of the system in the direction of the flow (high permeability flow pathway). Then we estimate the effective permeability of the heterogeneous porous media in different ways: a power law ($k_\mathrm{eff} =k_\mathrm{th} p^{m}$), a weighted power average ($k_\mathrm{eff} =\left[ {p\cdot k_\mathrm{th}^m +\left( {1-p} \right) \cdot k_\mathrm{g}^m } \right] ^{1/m}$ with $k_\mathrm{g}$ the geometric average of the permeability distribution) and a characteristic shape factor multiplied by the permeability threshold value. We found that the characteristic parameters (i.e., the exponent “m”) can be inferred either from the statistics and properties of percolation subnetworks at the threshold point (i.e., high and low permeable regions corresponding to those permeabilities above and below the threshold permeability value) or by comparing the system properties with an uncorrelated random field having the same permeability distribution. These physically based approaches do not need fitting to the experimental data of effective permeability measurements to estimate the model parameter (i.e., exponent m) as is usually necessary in empirical methods. We examine the order of accuracy of these methods on different layers of $10{\mathrm{th}}$ SPE model and found very good estimates as compared to the values determined from the commercial flow simulators.

1 Introduction

Hydrocarbon reservoirs are very heterogeneous due to the complex sedimentary processes and post-sedimentary events. The spatial distribution of heterogeneities, which appear on various length scales, may significantly influence the flow behavior and consequently the reservoir performance. Finite difference flow represents the reservoir with grid blocks with constant reservoir rock properties designed based on the level of heterogeneity considered in the geological modeling (Koltermann and Gorelick 1996). We need an appropriate estimate of ‘effective’ gridlock values (for the reservoir properties such as effective permeability) from fine grid geological models to be able to perform simulations within a practical time frame (Mattex and Dalton 1990). This process of deriving scale-adjusted physical properties of porous media is called upscaling and is an important subject in reservoir engineering (e.g., oil displacement by enhanced oil recovery process), and hydrology/hydrogeology (e.g., sequestration of carbon dioxide, sedimentation and diagenesis process).

Permeability is an important physical property that affects the subsurface flow and must be volumetrically averaged to scales larger than the representative elementary volume (REV) in heterogeneous porous media. At some scale larger than the Darcy scale we may use an effective permeability, $k_\mathrm{eff}$ by which we can account for the variation of the permeability at the small scale. This is an equivalent permeability of the upscaled region under steady state uniform flow conditions based on Darcy’s law which gives the proportionality between the average flow rate, q, and the average gradient, $\nabla {\varPhi }$ across a cross section of the porous medium, i.e., $q=-k_\mathrm{eff} \nabla {\varPhi }$. The criterion for representing the heterogeneous medium is usually considered as the same flow at the boundary of the domain of the heterogeneous medium subjected to the same pressure gradient (so called permeameter-type). Moreover, hydraulic conductivity which is the ratio of Darcy’s velocity to the applied hydraulic gradient describes the ease with which a fluid (usually water) can move through pore spaces. As emphasized by Renard and de Marsily (1997) there is a distinction between effective permeability, which is used for a statistically homogeneous medium on the large scale, and upscaled/block permeability of a finite size block, which is usually not statistically representative and depends on the block boundary conditions. As emphasized by Paleologos et al. (1996) under the ergodic hypothesis (i.e., equivalence between ensemble and spatial averages), which is justified for very large media, we can consider q and $\nabla {\varPhi }$ as spatial averages over the block of porous medium that is large compared to the spatial correlation scale of k(x). There is also a debate on the concept of the effective flow property in the literature which may depend on the pumping conditions, size and geometry of the domain and permeability spatial structure (Gomez-Herndndez and Gorelick 1989; Ababou and Wood 1990a, b).

Estimating the effective permeability is a challenge, because the correct values depend on various factors such as, the orientation and the degree of anisotropy of the heterogeneities, the volume fraction of the heterogeneities, permeability contrast between high and low permeable regions and continuity and connectivity of heterogeneities. The proposed method of estimation should work on very heterogeneous porous media with a broad distribution of the permeabilities, with various spatial distributions and anisotropic structural patterns and should account for the heterogeneity loss which is an indicator to show the degree of heterogeneity information lost during upscaling process (Ritzi et al. 2004; Ganjeh-Ghazvini et al. 2015). Usually, small-scale heterogeneity (i.e., due to grain size) can be accounted for by some kind of averaging procedure, while large-scale heterogeneity (i.e., due to the geological layers) can be considered by suitable layering. The most challenging cases are those with small to intermediate scales heterogeneities such as low-permeability barriers (Lasseter et al. 1986). Although the knowledge of permeability distribution at smaller scales can be used to estimate an upscaled transport property (Hunt 1998), the most likely value is related to the critical path (percolating) resistance.

There are different classifications of methods for calculating the effective permeability such as deterministic versus stochastic techniques, analytical versus numerical methods, exact versus approximate methods, and local versus non-local methods (see the detail of each in Renard and de Marsily 1997). The stochastic simulations have been used for addressing the effective hydraulic conductivity through either the Monte Carlo simulations for solving the stochastic governing partial differential equation (e.g., El-Kadi and Brutsaert 1985; Deutsch 1987; Desbarats 1987; Gomez-Herndndez and Gorelick 1989) or the analytical solution of the stochastic governing partial differential equation in which the parameters are regarded as random variables (Gutjahr et al. 1978; Dagan 1979). For example, El-Kadi and Brutsaert (1985) used the Monte Carlo simulations to evaluate the applicability of effective parameters for non-uniform flow on a medium with a lognormal distribution of hydraulic conductivity and an exponential covariance structure.

The analytical solution of the flow equation is only achievable on simple cases such as a stratified medium or a medium with lognormal permeability distribution. It can be determined for uniform flow while for non-uniform flow (e.g., non-local and non-Darcian) it is not existed (Neuman and Orr 1993). Hence, solving numerically (e.g., by using the finite difference or finite element methods) the governing partial differential flow equations with appropriate boundary conditions can be used for estimating effective permeability (Durlofsky 1991; Dykaar and Kitanidis 1992a, b; Neuman et al. 1992). The type of boundary conditions include permeameter-type, uniform or periodic conditions (Pickup et al. 1994). The numerical methods give results that are weakly biased depending on the method of calculating the inter block permeability and on the grid size (Romeu and Noetinger 1995). Dykaar and Kitanidis (1992a, (1992b) used a numerical spectral technique based on the Fourier Galerkin presented by Kitanidis (1990) for solving the flow equations with periodic boundary conditions and determine the effective flow property for multi-dimensional lognormal random permeability field in agreement with the other numerical or analytical results and applied to data of a shale and sandstone formation. Alternatively, renormalization techniques (King 1989) that uses arbitrary boundary conditions or other techniques (Renard and de Marsily 1997) with their advantages and disadvantages (i.e., limitations) can also be used. In this paper we use the statistics of the permeability map and stochastic methods based on percolation theory concepts for upscaling purposes. The first idea is to use only the permeability distribution function for upscaling. The arithmetic mean of the constituent permeability distribution in a sample volume is representative of the effective permeability when the sample volume is layered and the direction of flow is parallel to the layers. However, when the direction of flow is perpendicular to the layers, the harmonic average represents the effective permeability. When there is no spatial correlation among permeability values and variance of the permeability distribution is small, the geometric mean can represent the effective permeability of a 2D medium (King 1987; Drummond and Horgan 1987). In general, the effective permeability value lies between these two extremes (Cardwell and Parsons 1945; Warren and Price 1961). There are also other bounds proposed with their own specific applications (see Renard and de Marsily 1997 for the details of each). Under some simplified assumptions, other moments such as $\langle k^{1/3}\rangle ^{3}$ may work for a random lognormal permeability field (Desbarats 1992; Noetinger 1994).

Effective medium theory that ignores the topology of the system, power averaging methods, or perturbation theory that is restricted to local conductance distributions with small variability can also be used for estimating effective permeability (Kirkpatrick 1973; Bakr et al. 1978; Desbarats 1992). The effective medium approximations consider a medium plus some fluctuations and compare it with the medium itself which results in homogeneity and self-consistency. It is basically an improvement to dilute suspension method by considering the inclusion to be surrounded by a homogeneous medium of permeability $k_\mathrm{eff}$ (Hale 1976). Effective medium methods depend on the solution of an auxiliary problem that involves only a single medium inclusion. Then for problem that includes several inclusions we may use several methods based on the single-inclusion problem. Examples are: (1) the asymmetric self-consistent method, (2) the symmetric self-consistent method, and (3) the differential method (see Sævik et al. 2013 for more details). In these methods, the geometrical inclusions (such as spherical, ellipsoidal shapes) are considered within a homogeneous background. These approximations are known to be accurate for near-homogeneous mediums containing only a few non-intersecting inclusions (Torquato 2002).

The dilute suspension method assumes that the inclusions are well separated (i.e., unaffected by neighboring inclusions), and so they do not affect the streamline and gives simple estimation for the effective permeability. An improvement to this approximation is to use the self-consistent arguments (Milton 2002), i.e., by assuming that the neighborhood of each inclusion is a homogeneous material with the same medium’ effective permeability. For a porous medium that contains few randomly oriented inclusions (e.g., spheres with permeability $K_\mathrm{sh}$ and volume fraction $p_\mathrm{sh}$) in a continuous matrix (with permeability $K_\mathrm{ss}$, volume fraction $p_\mathrm{ss} =1-p_\mathrm{sh}$ with $p_\mathrm{ss} \gg p_\mathrm{sh}$) the dilute approximation gives (Maxwell 1873; McCarthy 1991),

$$\begin{aligned} k_\mathrm{eff} =k_\mathrm{ss} +\frac{3p_\mathrm{sh} k_\mathrm{ss}\left( {k_\mathrm{sh} -k_\mathrm{ss} } \right) }{2k_\mathrm{ss} +k_\mathrm{sh} } \end{aligned}$$

(1)

In the context of reservoir engineering, Begg and King (1985) used this statistical method to find the effective vertical permeability of a sandstone reservoir containing aligned rectangular shale,

$$\begin{aligned} k_\mathrm{eff} =\frac{k_\mathrm{ss}\left( {1-p_\mathrm{sh} } \right) }{\left( {1+n_\mathrm{sh} \cdot l_\mathrm{sh} /3} \right) ^{2}} \end{aligned}$$

(2)

where $n_\mathrm{sh}$ is the number density of shales, and $l_\mathrm{sh}$ is the mean shale length.

The effective medium theory used the idea that the mean fluctuation in the flow field due to the random inclusions (with no interaction among them) is almost zero and gives (Dagan 1979; Rubin 2003),

$$\begin{aligned} k_\mathrm{eff} =\frac{1}{d}\left( {\int \frac{f\left( k \right) \mathrm{d}k}{k+\left( {d-1} \right) k_\mathrm{eff} }} \right) ^{-1} \end{aligned}$$

(3)

where d is the dimensionality of the system, $f\left( k \right)$ is the permeability probability density function (pdf). Then for a medium with a bimodal distribution, such as a binary system with spherical inclusions in three dimensions with sand ($k_\mathrm{ss}$) and shale ($k_\mathrm{sh}$) permeability and sand fraction $p_\mathrm{ss}$, this becomes (Hale 1976; Dagan 1979; Desbarats 1987; Rubin 2003),

$$\begin{aligned} k_\mathrm{eff} =\frac{1}{3}\left( {\frac{1-p_\mathrm{ss} }{k_\mathrm{sh} +2k_\mathrm{eff} }+\frac{p_\mathrm{ss} }{k_\mathrm{ss} +2k_\mathrm{eff} }} \right) ^{-1} \end{aligned}$$

(4)

It is emphasized that under the non-uniform flow conditions, the effective permeability not only depends on the sand volume fraction ($p_\mathrm{s}$), but also depend on the other factors such as permeability spatial structure, the dimensionality of the flow system and the pumping rate (Desbarats 1987; Gomez-Herndndez and Gorelick (1989); Ababou and Wood 1990a, b).

Moreover, the power averaging methods can be used for estimating effective permeability. For example, Scheibe and Yabusaki (1998) used an empirical power law-scale averaging technique with calibrating parameter m as,

$$\begin{aligned} k_\mathrm{eff} =\left( \int \nolimits _{k_{\mathrm{min}} }^{k_{\mathrm{max}} } k^{m}f\left( k \right) \mathrm{d}k \right) ^{1/m} \end{aligned}$$

(5)

where $k_{\mathrm{max}}$ and $k_{\mathrm{min}}$ stand for the largest and smallest permeability values, respectively. The exponent ‘m’ is between $-1$ and 1 with $m=1$ showing the arithmetic mean of the elements in the subdomain; and $m=-1$ gives the harmonic mean. As m approaches zero, the effective permeability approaches the geometric mean. It is emphasized that the value of $m>0$ ($m<0$) favors the importance of the largest (smallest) permeability values in the permeability distribution. However, power averaging methods implies isotropic value, i.e., lack of directional dependence, of effective permeability at all scales. Moreover, the role of high conductive path ways observed in numerical simulations or field observations (Bernabe and Bruderer 1998; Knudby and Carrera 2006) is not supported by the power law averaging schemes. In a binary medium made up of a mixture of two distinct phases (such as sand–shale reservoirs) the effective permeability as a power average of the component permeabilities becomes (Deutsch 1989; Ababou 1990),

$$\begin{aligned} k_\mathrm{eff} =\left[ {p_\mathrm{ss} k_\mathrm{ss}^m +\left( {1-p_\mathrm{ss} } \right) k_\mathrm{sh}^m } \right] ^{1/m} \end{aligned}$$

(6)

where the exponent ‘m’, which depends on the medium spatial structure, is inferred from the measurements.

In addition, the analytical approach can be used to estimate the effective permeability which follows the Matheron conjecture that is for lognormally distributed permeability in d dimensions, the effective permeability is the weighted average of the arithmetic ($k_\mathrm{ar}$) and harmonic ($k_\mathrm{h}$) means as (Matheron 1967),

$$\begin{aligned} \ln k_\mathrm{eff} =\left( {1-\frac{1}{d}} \right) \ln k_\mathrm{ar} +\frac{1}{d}\ln k_\mathrm{h} \end{aligned}$$

(7)

which, on a lognormal medium (by using relation $k_{\mathrm{ar}} =k_\mathrm{g} e^{{\sigma }_{\mathrm{ln}k}^2 /2}$ and $k_{\mathrm{ar}} =k_\mathrm{g} e^{{-\sigma }_{\mathrm{ln}k}^2/2}$ for the arithmetic and harmonic means, respectively) with small variance ($\sigma _K^2$) and uniform flow this is (Landau and Lifshitz 1960; Gutjahr et al. 1978; Dagan 1979; De Wit 1995; Rubin 2003),

$$\begin{aligned} k_\mathrm{eff} =k_\mathrm{g} e^{\left( {\frac{1}{2}-\frac{1}{d}} \right) \sigma _{\mathrm{ln}k}^2 } \end{aligned}$$

(8)

where $d=1, 2,$ or 3 is the dimensionality of the system and $k_\mathrm{g}$ is the geometric mean, i.e., $k_\mathrm{g} =e^{\langle {\mathrm{ln}k}\rangle }$. This gives exact value in one dimension (i.e., the harmonic mean), leads to $k_{\mathrm{eff}} =k_\mathrm{g}$ in two dimensions and becomes a truncated perturbation expansion in three dimensions. Moreover, stochastic analytical and numerical results for lognormal permeability models under small perturbation gives the approximate effective permeability equivalent to the first-order Taylor’s series expansion of the exponential term in Eq. (8) as (Bakr et al. 1978; Moreno and Tsang 1994):

$$\begin{aligned} k_\mathrm{eff} =k_\mathrm{g} \left[ {1+\left( {\frac{1}{2}-\frac{1}{d}} \right) \sigma _{\mathrm{ln}k}^2 } \right] \end{aligned}$$

(9)

This reduces to for,

$$\begin{aligned} 2\mathrm{D}{:}\quad k_\mathrm{eff}= & {} k_\mathrm{g} \end{aligned}$$

(10)

$$\begin{aligned} 3\mathrm{D}{:}\quad k_\mathrm{eff}= & {} k_\mathrm{g} \left( {1+\frac{\sigma _{\mathrm{ln}k}^2 }{6}} \right) \quad \mathrm{for}\quad \sigma _{\mathrm{ln}k} <2 \end{aligned}$$

(11)

Neuman and Orr (1993) found that in 2D, away from a pumping well and from the outer boundary, the geometric mean dominates even for $\sigma _{\mathrm{ln}k}> 4$. In the presence of statistical anisotropy or spatial correlation Eq. (11) may give poor estimation. For example, Moreno and Tsang (1994) showed that for larger standard deviations $(\sigma _{\mathrm{ln}K} >2)$ the effective permeability is much larger than the estimation from Eq. (11) due to the appearance of the flow channeling. Moreover, this estimation may not be satisfactory in the presence of spatial correlation in the medium. Also this method of approximation (Eq. 8) has been extended to take into account the effects of anisotropy (Ababou 1995; Neuman 1994). Moreover, this effective permeability behavior (Eq. 8) becomes different for the “radial flow” induced by pumping wells in a randomly heterogeneous medium (Ababou and Wood 1990a, b). It is emphasized that the role of connectivity of either very high conductive pathways or flow barriers, which appears to be important near the percolation threshold, cannot be considered in homogeneous based approach with self-consistency; hence, other techniques based on the topology information are necessary.

Alternatively, percolation theory which relates the topology of random binary permeability fields to the occupancy probability (Stauffer and Aharony 1992) can be used to estimate the effective permeability for binary permeability fields in which each gridlock being either permeable such as sandstones or impermeable such as shales (Berkowitz and Balberg 1993; Sahimi 1993). However, the reservoir permeability distribution never follows this kind of permeability distribution and usually there is a broad distribution of permeability in the gridlock, often this can be represented as a lognormal distribution. It is suggested to treat the power laws obtained from percolation theory to estimate the effective permeability as an empirical model with two adjusting parameters obtained by fitting a variety of experimental data gathered from permeability measurements (McLachlan 1987; McCarthy 1991). In real cases the methods for estimating the effective permeability should account for both the effects of permeability distribution and the topology.

Field observations show that there exists preferential flow pathways formed through the connected high permeable regions (i.e., flow channels or pathways as noted by Moreno and Tsang 1994) that spans across the reservoir (Ambegaokar et al. 1971). For example, Moreno and Tsang (1994) show this numerically by calculating the tracer breakthrough curves for a pulse injection into a lognormal permeability distribution and see that at a high standard deviation two peaks appears in the breakthrough plot; one emerges at a much earlier time showing the channeling effect. The behavior of the high permeability cells (i.e., the lowest resistance) in the model is affected by anisotropy, correlation, and lattice size (Guin and Ritzi 2008). Moreover, the details description of flow through porous media consists of high permeable cells may need other information such as tortuosity or constriction factor (Berg 2014).

Katz and Thompson (1985) conjectured that single phase flow in disordered porous medium is largely controlled over a connected critical path consisting of pores of sufficiently high permeability that spans the region. The idea is extended to a random porous medium with the permeability distribution $f\left( k \right)$. Each cells in the connected cluster with an occupied fraction p has a permeability value greater than or at least equal to the threshold permeability ($k\ge k_\mathrm{th}$), then from percolation theory the percolation-type power law scaling (e.g., Eq. 18) can be used to estimate the effective permeability of such a medium. Critical path analysis may treat the smaller resistances in the system as in being in series which gives an approximation (Hunt and Idriss 2009),

$$\begin{aligned} k_\mathrm{eff} =\frac{k_\mathrm{ar} k_{\mathrm{h}+} }{k_{\mathrm{max}} } \end{aligned}$$

(12)

where $k_\mathrm{ar}$ is the arithmetic average of the permeability distribution, $k_{\mathrm{h}+}$ is the harmonic average of the high permeable values (i.e., those above the percolation threshold) and $k_{\mathrm{max} }$ is the highest permeability value. It is emphasized that the choice of the normalization factor in the denominator of Eq. (12) works in mono-modal distributions, but may fail in the case of bimodal distributions when the higher permeability mode does not percolate.

The concept of high permeable pathways has been extended to estimate the effective permeability for systems with lognormal distributions (Shah and Yortsos 1996; Hunt and Idriss 2009). For example, Shah and Yortsos (1996) proposed an implicit method to estimate the effective permeability that is depend on the standard deviation ($\sigma$) of a porous media with a lognormal permeability distribution as,

$$\begin{aligned}&k_\mathrm{eff} \sim \sigma ^{-\mu }\hbox {exp}\left( {\ln \left( {\frac{k_\mathrm{th} }{k_\mathrm{g} }} \right) +\mu \left[ {\frac{\ln \left( {k_\mathrm{th} /k_\mathrm{g} } \right) }{\sigma \sqrt{2}}} \right] ^{2}} \right) \end{aligned}$$

(13)

$$\begin{aligned}&\mathrm{erf}c\left( {\frac{\ln \left( {k_\mathrm{th} /k_\mathrm{g} } \right) }{\sigma \sqrt{2}}} \right) =2p_\mathrm{c} +\frac{\mu \cdot e^{-\left[ {\frac{\ln \left( {k_\mathrm{th} /k_\mathrm{g} } \right) }{\sigma \sqrt{2}}} \right] ^{2}}}{\sigma \sqrt{\pi /2}} \end{aligned}$$

(14)

where $\mu$ is the conductivity exponent and $p_\mathrm{c}$ is the critical occupancy called the percolation threshold. Hunt and Ewing (2005) proposed an approximate effective permeability of a medium with a bimodal permeability distribution (e.g., for sand and mud deposits) as,

$$\begin{aligned} k_\mathrm{eff} =\frac{L}{\frac{L-\xi }{k_\mathrm{th} }+\frac{\xi }{k_{\mathrm{g}+} }} \end{aligned}$$

(15)

where L is the length of the sample, $k_\mathrm{th}$ the permeability threshold, $k_{\mathrm{g}+}$ the geometric mean for the high permeability values and $\xi$ is the correlation length of high permeable values. Hunt and Idriss (2009) used a power law interpolating scheme similar to that of Scheibe and Yabusaki (1998) for estimating the effective permeability of a medium with a bimodal permeability distributions with two distributions and propose,

$$\begin{aligned} k_\mathrm{eff}= & {} k_\mathrm{g} \left( {1-p_\mathrm{ss} } \right) \quad \mathrm{for}\quad p_\mathrm{ss} <p_\mathrm{c} \end{aligned}$$

(16a)

$$\begin{aligned} k_\mathrm{eff}= & {} k_\mathrm{g} \left( {1-p_\mathrm{ss} } \right) +k_{\mathrm{g}+} \left( {\frac{p_\mathrm{ss} -p_\mathrm{c} }{1-p_\mathrm{c} }} \right) ^{2}\quad \mathrm{for}\quad p_\mathrm{ss} >p_\mathrm{c} \end{aligned}$$

(16b)

where $p_\mathrm{ss}$ is the fraction of cells with permeability value greater than $k_\mathrm{th}$. When the upper mode of the permeability distribution did not percolate then Eq. 16 can be substituted for Eq. (12). In general, a hybrid between the two estimations (Eqs. 12, 16) may be used. Moreover, the critical path analysis has been linked to the solute transport as the solute is likely to move through clusters with minimum conductance (Ghanbarian-Alavijeh et al. 2012). Hence, the knowledge about the distributions of arrival times from solute transport may be used to estimate the effective permeability.

So far percolation theory method to estimate the effective permeability of heterogeneous porous medium has been treated as an empirical model which needs some adjusting parameters from a variety of experimental data (McLachlan 1987; McCarthy 1991). In this paper we present methods to estimate the effective permeability of heterogeneous porous media with a broad distribution of permeabilities and various underlying structures based on percolation concepts. The main contribution is to show that these methods do not need fitting to the experimental data of permeability measurements to estimate the model parameters as was necessary in the previous empirical models. We examine these methods on different layers of $10{\mathrm{th}}$ SPE model and compare the results with the values determined from the numerical flow simulators for validation.

2 Percolation Theory Approach

Percolation theory is used to investigate the connectivity and conductivity behavior of geometrically complex systems made by objects distributed randomly in an impermeable background. It enables us to make the predictions through some simple power laws. This approach has many applications including in hydrology and petroleum engineering (Berkowitz and Balberg 1993; Sahimi 1994; King 1990; Mourzenko et al. 2005; Masihi et al. 2007; Sadeghnejad et al. 2013)

This theory initially applied on lattices, i.e., site or bond percolation (e.g., Stauffer and Aharony 1992) and the extended to systems made of geometrical shapes randomly distributed in the system called continuum percolation (e.g., Berkowitz 1995; King 1990). There are other types of percolation such as correlated percolation (Lee and Torquato 1990; Prakash et al. 1992), directed percolation or dynamic percolation (Wilkinson and Willemsen 1983).

Consider a reservoir made of good rocks with high porosity and permeability (e.g., clean sandstones, fractures) that contain the majority of the hydrocarbon fluids and poor rock types with very low or no porosity and permeability (e.g., shale, mud stone, siltstone). Examples include reservoirs formed in fluvial (King 1990) or turbidite (Mayall et al. 2006) depositional environments: for example, channelized reservoirs formed from meandering rivers which deposits sand layers over the time [see Figure 1 in Nurafza et al. (2006) for a typical sandbody model formed] and turbidite channel deposits in an impermeable background. To construct such sandbody models we can use an object based modeling approach (where sands are represented as geometrical objects and distributed in the system) or grid-based modeling approach (such as indicator kriging) from geostatistical modeling techniques (Deutsch 2002; Caers et al. 2005).

It is clear that the amount of producible hydrocarbon between two injection and production wells located in such a system is directly related to the connected volume of hydrocarbon in good rock types distributed between two the wells. Percolation theory uses the hypothesis that the permeability in such reservoirs can be split into either permeable or impermeable and neglects the heterogeneities encountered within the permeable rock types (Hunt and Idriss 2009). It assumes that the flow paths are mainly controlled by the connectivity of flow units and not strongly modified by the flow dynamics themselves (King 1990). It is shown numerically by Desbarats (1987) on a conceptual sand–shale model that at lower sand occupation fractions, where the continuity of the sandstone phase is broken, and the flow is controlled by the shale permeability.

We consider a simple continuum percolation model made up by random distribution of good sands with specific geometrical shapes (so called sandbodies which are represented by squares in 2D or cubes in 3D) within an impermeable background (e.g., shale) and define the sand occupation fraction (or reservoir net-to-gross, NTG), p, to be the area (in 2D) or volume (in 3D) fraction of the reservoir occupied by the good sands. This corresponds to the probability that a random point in space is lying within the permeable rock. In classic site percolation, clusters of permeable sites are formed when neighboring sites are occupied. In continuum models, clusters are formed by intersection of two or more permeable bodies. As p increases, clusters of permeable sites (or sandbodies) grow in size and at a specific occupancy (or sand fraction) called the percolation threshold, $p_\mathrm{c}^\infty$ (the superscript $\infty$ denotes the infinite size system), a connected or spanning cluster spans the entire system. There are also other small clusters which get absorbed as p further increases. For the simplest model, which is an infinite size lattice of sites of square shape (called site percolation) this critical value is about $p_\mathrm{c}^\infty =0.59275$ (Stauffer and Aharony 1992). However, this critical occupation is slightly changed for finite size systems.

The first percolation quantity to consider is the percolation probability $P\left( p \right)$ which is defined as the probability that any occupied site belongs to the spanning cluster for a given value of p. This dimensionless percolation quantity is basically the connected sand fraction (i.e., the number ratio of cells occupied by the sands in the connected sand cluster to the total number of cells occupied by the sands) and also called connectivity in percolation literature. There is a similar quantity to the percolation probability (P) that is called spanning probability $\varPi$. This is the probability that a connected cluster exist across the system. For an infinite system it has a step function behavior, i.e., $\varPi =0$ for $p<p_\mathrm{c}$ and $\varPi =1$ for $p>p_\mathrm{c}$. It is reminded that the percolation probability (P) is the strength of the connected cluster. We used the same notations p and P as conventionally used in percolation literature where p in the lower case represents the total sand fraction in the medium while the upper case P represents the connected sand fraction. We can use standard algorithm from percolation theory to characterize various clusters in each realization, generate different realizations and get reasonable statistics of the percolation quantities such as P at various systems sizes.

The second important percolation quantity is the effective permeability ($k_\mathrm{eff}$) of the system. In the binary permeability system, it is usually normalized by the permeability of sands ($k_\mathrm{ss}$), i.e., the permeability of the medium when all grid cells are occupied by sands, i.e., $p=1$. From percolation theory it is well known that the percolation probability (P) and the effective permeability ($k_\mathrm{eff}$) of infinite systems follow power law scaling (Stauffer and Aharony 1992):

$$\begin{aligned}&P\left( p \right) \propto \left( {p-p_\mathrm{c}^\infty } \right) ^{\beta } \end{aligned}$$

(17)

$$\begin{aligned}&k_\mathrm{eff} \left( p \right) \propto \left( {p-p_\mathrm{c}^\infty } \right) ^{\mu } \end{aligned}$$

(18)

where $p_\mathrm{c}^\infty$ is the percolation threshold of an infinite size system, $\beta$ is the connectivity exponent and $\mu$ is the effective permeability exponent. These laws are universal which means that the exponents are independent of detail of system (i.e., local geometries and the type of percolation) and they are only depend on dimensionality of the system (i.e., 2-D or 3-D). However, in systems made by geometrical objects with very broad length distribution or systems with very long range spatial correlation of heterogeneities the critical exponents may change (Prakash et al. 1992; Schmittbuhl et al. 1993; Sahimi and Mukhopadhyay 1996; Masihi and King 2007, 2008). When the permeability of all the occupied sites is, for example, $k_1$, the constant of proportionality in the scaling law (Eq. 18) becomes $k_1$.

In reality, geological formations are finite in size, which limits the application of Eqs. (17) and (18). In such situations, the calculated connected sand fractions not only depend on the sand occupation fraction (p) but also vary with the system size, i.e., $P\left( {p,L} \right)$. In finite size systems there is no longer a sharp transition in the connected sand fraction near the threshold described by power law in Eq. (17) so the main effect of finite boundaries is to smear out the percolation transition (i.e., we observe a scatter of points for the plot of $P\left( {p,L} \right)$ against p data). Instead of working with whole scatter we can determine the mean connected sand fraction and the standard deviation around it. There is finite size scaling laws within percolation theory which describes the mean and standard deviation behavior. Similarly finite size scaling can be used to treat the effects of finite boundaries on the effective permeability results. For example, the finite size scaling laws for the mean connected sand fraction and the mean effective permeability become (Stauffer and Aharony 1992),

$$\begin{aligned} P\left( {p,L} \right)= & {} L^{-\beta /v}F\left[ {\left( {p-p_\mathrm{c}^\infty } \right) L^{1/v}} \right] \end{aligned}$$

(19)

$$\begin{aligned} k_\mathrm{eff} \left( {p,L} \right)= & {} L^{-\mu /v}g\left[ {\left( {p-p_\mathrm{c}^\infty } \right) L^{1/v}} \right] \end{aligned}$$

(20)

where L is the dimensionless system size defined as the ratio of system size X to the sand size a (i.e., $L=X/a)$, F and g are the master curves for the mean connected sand and mean effective permeability functions respectively. The well data, permeability map, and facies map can be used for estimation of thickness and lateral extensions of the sands. Moreover, the master curves F and g for the problem (e.g., overlapping sandbody model) can be determined by building an object-based model for the problem and performing some Monte Carlo simulations.

Moreover, the standard deviation in these percolation quantities (i.e., P and $k_\mathrm{eff}$) can be determined from percolation scaling laws (see Masihi et al. 2007 for more details). The typical connected sand fraction and effective permeability master curves (F and g) for isotropic sand body model and randomly oriented fracture networks can be found in elsewhere (King 1990; Masihi et al. 2007; Sadeghnejad et al. 2010). The developed master curves can be encoded in a spreadsheet to estimate the effective permeability very quickly.

However, the real field permeability maps do not satisfy the assumptions used in percolation theory. Usually the permeability distribution of hydrocarbon reservoirs is not as a binary permeability field (i.e., grid blocks to be either permeable or impermeable) as assumed in classic percolation theory. Often the permeability distribution can be characterized by a very broad distribution such as a lognormal distribution. Moreover, in reality the spatial distributions of permeability maps are neither isotropic nor uncorrelated. The effect of anisotropy or the existence of spatial correlation in the permeability distribution results in different percolation threshold along the x or y axis and consequently a shift in the percolation quantities such as the connected sand fraction and the effective permeability master curves (see Masihi et al. 2006; Sadeghnejad et al. 2010 for more details on the impact of anisotropy on percolation quantities). Estimation of the effective permeability in such practical cases is a challenge. In the subsequent sections we will see how to make these estimations.

3 $10{\mathrm{th}}$ SPE Model

The $10{\mathrm{th}}$ SPE model, is a geostatistical realization from the Jurassic Upper Brent formation that consists of $60 \times 220 \times 85$ grid cells, each of size $20\,\hbox {ft} \times 10\,\hbox {ft} \times 2\,\hbox {ft}$ (Christie and Blunt 2001). The top 35 layers (70 ft) represent the shallow marine Tarbert formation which consists of sandstone, siltstone, and shales and the lower 50 layers (100 ft) represents the fluvial Ness formation that made of well-sorted highly permeable long correlation sandstone channels imposed on a low-permeable background of shales and coal.

The permeability model is highly heterogeneous and is used in a large number of publications especially for upscaling purposes. There is a large permeability variation (8–12 orders of magnitude) in the model with significant differences in the types of permeability distributions in the top and lower layers.

It is observed that no single statistical moment, such as harmonic mean, arithmetic mean, or geometric average is able to represent the effective permeability of the layers. However, the effective permeability is bounded by the arithmetic and harmonic means of the permeability distribution function.

In subsequent sections we will see how we can use percolation concepts to get suitable estimation of the effective permeability of this very heterogeneous model.

4 Methodology

It has long been understood that the flow in heterogeneous porous media is largely controlled by the continuity of permeability contrasts, e.g., barriers such as shales or high permeability zones such as channels (Moreno and Tsang 1994). Although there are other influences, it is believed that these are the predominant features affecting the flow behavior. With this in mind, we are looking for the methods to estimate the effective permeability which concentrate on the connectivity of the permeability contrasts.

Fig. 1

A schematic permeability cumulative probability function (cdf) to illustrate the threshold permeability value ($k_\mathrm{th}$) and the fraction of cells (p) occupied by high permeable values ($k>k_\mathrm{th}$)

Let consider a general two-dimensional reservoir permeability map with any spatial distribution of permeability values and a given probability density distribution. To illustrate the definition of parameters needed later a schematic of the cumulative distribution of permeability is shown in Fig. 1. In practice, we want to study the flow behavior in a very heterogeneous reservoir and estimate its effective permeability, for example along the y-axis in Fig. 2 that is one of the permeability map of $10{\mathrm{th}}$ SPE model. Based on the argument mentioned before, it is the grid blocks with high permeability values that effectively contribute to the flow; while, the flow in grid blocks with very low permeability values is negligible. Moreover, it is important to make sure that there is connection between grid blocks through grid blocks with high permeability values along the flow direction (i.e., along the y axis). In percolation terminology, this means that we must have a connected (or percolating) cluster of high permeable cells that connect the two opposite sides of the system along the y axis.

4.1 Connected Cluster of High Permeability Values

To find the connected cluster of cells with high permeability values on a given permeability map (such as the permeability map shown in Fig. 2), we choose a threshold value ($k_\mathrm{th}$) starting from the highest permeability value of the permeability distribution and examine if the cells with permeabilities $k>k_\mathrm{th}$ make a connected path along the y-axis by using the standard algorithm (Hoshen and Kopelman 1976). If the connection does not exist at the selected threshold value ($k_\mathrm{th}$) we choose a smaller permeability value and repeat this until the connected cluster appears for the first time (such as those shown in Fig. 2). Then the fraction of cells occupied by high permeability values ($k>k_\mathrm{th}$) is called the occupancy fraction (p) which is the region shown in Fig. 1 and its corresponding permeability value is called the threshold permeability value ($k_\mathrm{th}$). In fact the $k_\mathrm{th}$ is the value at which the $1{\mathrm{st}}$ percolating cluster appears. As emphasized by Hunt and Ewing (2005) this threshold value depends on the topology of the network. The value of the threshold also depends on the direction considered for the analysis (e.g., in linear or radial flow geometries), and the nature of percolation connection; for example in two-dimensional problems, the connection between two lines perpendicular to flow direction (as was used in this study) or connection between two points representing two wells (Tavagh-Mohammadi et al. 2016).

Now we assume that this connected cluster is the main flow path that controls the flow behavior within the system. The concept of high permeability path is consistent with the fact that in high disordered media only a small subset (similar to the backbone in percolation theory) of high permeable elements contributes to the overall flow.

It is emphasized that there also exist other finite non connected smaller (relative to the connected cluster) clusters of high permeable values in the system that have just local conductivity effects (see these along with the connected cluster in Fig. 2).

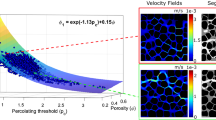
To see the effects of applying the permeability threshold, two different layers of $10{\mathrm{th}}$ SPE model are used. Figure 2 shows the original permeability map which is a correlated geostatistically generated field (Christie and Blunt 2001), the structure of the connected cluster and the connected cluster along with other finite smaller clusters for layers 14 (from top layers of $10{\mathrm{th}}$ SPE model with non-channelized pattern) and layer 57 (from lower layers of $10{\mathrm{th}}$ SPE model with channelized pattern).

Fig. 2

Examples of a the original permeability map, b only the connected cluster of high permeability values along the y-axis , c the connected cluster along with other finite smaller clusters and d permeability distribution function (top) for layer 14 (at $p=0.798, P=0.958$ and $k_\mathrm{th} =6.89\,\mathrm{md})$ and (bottom) for layer 57 (at $p=0.468, P=0.540$ and $k_\mathrm{th} =106.84\,\mathrm{md})$ of $10{\mathrm{th}}$ SPE model. Yellow shows the area occupied by high permeability values ($k>k_\mathrm{th}$)

It should be emphasized that the shape of connected cluster depends on the spatial distribution of permeability values in the domain. For example, let use the same permeability values of layers 14 and 57 consistent with the original permeability distributions in Fig. 2 and distribute them randomly in space to generate corresponding uncorrelated random fields for layer 14 and 47. Unlike the original permeability map of layers 14 and 17, these generated permeability fields are statistically homogenous and isotropic. Similarly, by using the same permeability statistics we generated many realizations of such uncorrelated fields. For these uncorrelated permeability fields, we can then determine another permeability threshold value (called the threshold value for the uncorrelated random field $k_{\mathrm{th}\text {-}\mathrm{rand}}$) at which a cluster of high permeability values spans the region for the first time (see Fig. 3 for two realizations showing the connected clusters along the y-axis at the threshold point). Having determined the onset of connection in the medium for all realizations, we can find the statistics of the permeability threshold.

Fig. 3

Two realizations of spatially uncorrelated permeability maps with the same original permeability distributions of $10{\mathrm{th}}$ SPE model shown in Fig. 2, (left) for layer 14 at $p=0.6256, P=0.794$ with $k_{\mathrm{th}\text {-}\mathrm{rand}} =20.93\,\mathrm{md}$ and (right) for layer 57 at $p=0.6442, P= 0.915$ with $k_{\mathrm{th}\text {-}\mathrm{rand}} =23.70\,\mathrm{md}$ showing the connected clusters of cells with high permeability values ($k>k_{\mathrm{th}}$) in yellow

The spatial configuration of the connected clusters of high permeability values ($k>k_{\mathrm{th}}$) in the real permeability maps (in Fig. 2) and its corresponding uncorrelated randomly generated realizations (in Fig. 3) can be quantified by calculating the fractal dimension (D) of the connected clusters in each model (Hunt and Ewing 2005). Fractal dimension is determined by using the box counting method by which the permeability domain of size L is covered by a grid of size r. Boxes inside which the connected cluster (i.e., cells with high permeability values $k>k_{\mathrm{th}}$) is presented are counted N(r). Then N(r) is plotted against r. The slope of log–log plot of N(r) versus r provides the fractal dimension (Mandelbrot 1982). From percolation properties, there is a unique value for the fractal dimension of the connected cluster in uncorrelated systems (i.e., $D=1.89)$; while, smaller or greater values can be calculated in the more general correlated or anisotropic real permeability maps. For example, a comparison of the computed fractal dimensions of the connected clusters in all 85 layers of $10{\mathrm{th}}$ SPE model is shown in Fig. 4 which clearly shows a difference in the structure of the top and lower layers of $10{\mathrm{th}}$ SPE model. Figure 4 shows the fractal dimensions of lower 50 layers (layers 35–85) are much below 1.89 (that is for random system) emphasizing that the permeability spatial distributions of these layers show fractal structures with very broad correlation length (e.g., channelized structure).

Fig. 4

The numerical values of the fractal dimensions of the connected clusters calculated in all 85 layers of $10{\mathrm{th}}$ SPE model

Fig. 5

The cross-plot the determined threshold permeability values ($k_{\mathrm{th}\text {-}\mathrm{rand}}$) from percolation algorithm when the connected cluster appears and the numerically computed effective permeability from Eclipse from several realizations of lognormal permeability distributions with the mean value of 300 md but at four different dispersion ranges (i.e., CV $=$ 0.5, 1, 2 and 3) in a system of size $220\times 60$

It is noted that the threshold permeability values ($k_{\mathrm{th}\text {-}\mathrm{rand}}$) obtained in uncorrelated random fields with a given permeability probability density function are very close to the effective permeability determined from the pressure solver method (e.g., by using commercial software such as Eclipse). To see this, we have generated several uncorrelated random fields with a lognormal permeability distribution function with the arithmetic mean of 300 md but at four different dispersion levels (e.g., at four coefficient of variations CV $=$ 0.5, 1, 2 and 3 defined as the ratio of standard deviation to the arithmetic mean) in a system of size $220\times 60$ which is similar in size to the $10{\mathrm{th}}$ SPE model.

We produced several realizations of such permeability distributions and then calculated the threshold permeability values ($k_{\mathrm{th}\text {-}\mathrm{rand}}$) using the percolation algorithm described in Sect. 4.1 and compared them with the computed effective permeability determined from Eclipse which solved the steady-state flow equation for single-phase incompressible fluid flow subjected to fixed pressure drop across the reservoir in the direction of flow (i.e., along the y-axis in Fig. 3) with both wells completed in all boundary grids and no flow conditions perpendicular to the flow direction (see results of 20 realizations in Fig. 5).

Let emphasize that we first fond the $k_\mathrm{th}$ in each realization and then determined the occupied fraction p. The average occupied fraction (p) of high permeable cells along the y-axis over all realizations was $p=0.62$. The difference between this value and the infinite threshold value in site percolation (i.e., $p_\mathrm{c} =0.593$) as emphasized by Masihi et al. (2006) is due to the anisotropy of the system caused by different effective size of the system in the x and y directions which results in a shift in the threshold value appearing in the longer direction of the system (i.e., the y-direction). Now for each permeability distribution function, consider the threshold permeability value along the y-axis (the representative permeability threshold over all realizations) to be the threshold permeability value that gives $p=0.62$ (i.e., the $62{\mathrm{nd}}$ percentile). It is emphasized that once we use this, the difference between the permeability threshold value and the effective permeability calculated by Eclipse is very small (e.g., it is less than 3 % in the case of lognormal distribution with CV $=$ 3). A similar variance-independent approximation has also been used for two-dimensional uncorrelated lognormal permeability models in literature as given by Eq. (10). We will use the permeability threshold value ($k_{\mathrm{th}\text {-}\mathrm{rand}}$) obtained at $p=0.62$ as the representative permeability threshold of uncorrelated random fields in subsequent sections.

Let now move to more general real permeability models which may be anisotropic and spatially correlated. We present four different approaches to estimate the effective permeability of such a non-binary (e.g., with lognormal distribution) heterogeneous model based on the statistics of the permeability distribution and the configuration of the connected cluster of high permeable values appears at the threshold point. For the rest of this paper when we refer to the threshold, we mean a point at which for the first time a cluster of cells with high permeability values (i.e., $k>k_\mathrm{th}$) connects the region along the flow direction. Moreover, we use notation $k_\mathrm{est}$ to represent the estimated value for the effective permeability from the proposed percolation-based methods and compared with the effective permeability computed numerically from a commercial flow simulator ($k_\mathrm{eclipse}$). It is emphasized that this is the effective permeability determined along the flow direction, i.e., the principal direction of anisotropy (e.g., the y-axis in Figs. 2 or 3). In the following section we first describe different percolation-based methods of estimating the effective permeability and then present their results.

4.2 The Threshold Value ($K_\mathrm{th}$)

In this approach, we use the permeability threshold value ($k_\mathrm{th}$) at which for the first time a cluster of cells with high permeability values (i.e., $k>k_\mathrm{th}$) spans the region along the flow direction (i.e., the y-axis) as a first estimate of the effective permeability.

$$\begin{aligned} k_{\mathrm{eff}\text {-}\mathrm{est}} =k_\mathrm{th} \end{aligned}$$

(21)

This can be thought as a power average of the component permeabilities (Eq. 6 by Scheibe and Yabusaki 1998) in a binary medium made by high permeable and low permeable cells with occupation fraction p and $1-p$, respectively, while both phases have permeability equal to $k_\mathrm{th}$.

4.3 A Weighted Power Average Between the Threshold Value and Geometric Mean of Permeability Distribution

To estimate the effective permeability in this approach, we hypothesize a weighted power average between the permeability threshold value ($k_\mathrm{th}$) appeared in the flow direction (i.e., the y-axis) for the first time and the geometric mean of the permeability distribution ($k_\mathrm{g}$) defined as,

$$\begin{aligned} k_{\mathrm{eff}\text {-}\mathrm{est}} =\left( {pk_\mathrm{th}^m +\left( {1-p} \right) k_\mathrm{g}^m } \right) ^{1/m} \end{aligned}$$

(22)

This considers both the effects of permeability distribution and the topology of the high conductance pathways. An appropriate way to estimate the value for the exponent “m” can be considered in following different ways:

• (A) The exponent “m” is assumed to be one that is consistent with the assumption that the flow move through two parallel layers with permeability of $k_\mathrm{th}$ and $k_\mathrm{g}$,

  $$\begin{aligned} m=1 \end{aligned}$$

  (23)

• (B) The exponent “m” is assumed to be the fractal dimension of the percolation minimal path known as one of the percolation subnetworks that is the shortest path between two points on the percolation cluster (Havlin and Nossal 1984; Nikolay et al. 1999).

  $$\begin{aligned} m=1.13 \end{aligned}$$

  (24)

• (C) The exponent “m” is assumed to be the ratio of the fractal dimension of the connected clusters in two cases. The first case is the connected clusters of the real permeability map with given permeability probability density function. The second case is the connected clusters of the uncorrelated random field with the same permeability probability density function as the real one, i.e.,

  $$\begin{aligned} m=\frac{1.89}{D} \end{aligned}$$

  (25)

  where 1.89 is the fractal dimension of percolating cluster in two dimensions.

4.4 A Power Law Function of Occupancy Probability (p) Scaled by the Threshold Value ($K_\mathrm{th}$)

To estimate the effective permeability in this approach, we hypothesize a power law function of high permeable occupancy (p) scaled by the permeability threshold value ($k_{\mathrm{th}}$) appears in the flow direction (i.e., the y-axis) for the first time,

$$\begin{aligned} k_{\mathrm{eff}\text {-}\mathrm{est}} =k_\mathrm{th} \cdot p^m \end{aligned}$$

(26)

This is a generalized percolation-type power law function with exponent “m” as a characteristic parameter that may capture some of the effects of the shape of connected clusters, anisotropy, correlation and spatial distribution of high permeability values that describes the heterogeneity of the system. McCarthy (1991) also emphasized that this exponent depends on the shape of the inclusions and whether they are oriented, partially oriented, or random in the binary percolation medium. This method considers the topology of the high conductive pathways. Moreover, the exponent m can be estimated in such a way that takes into account the effect of permeability distribution. An appropriate value for the characteristic parameter (exponent “m”) can be inferred in the following different ways:

• (A) The exponent “m” is inferred from equality of the permeability threshold value ($K_\mathrm{th}$) and the weighted power average between the geometric mean ($k_{\mathrm{g}-}$) of permeability values below the threshold (i.e., $k<k_\mathrm{th}$) and the geometric mean ($k_{\mathrm{g}+}$) of permeability values above the threshold ($k>k_\mathrm{th}$) i.e.,

  $$\begin{aligned} k_\mathrm{th} =\left( {pk_{\mathrm{g}+}^m +\left( {1-p} \right) k_{\mathrm{g}-}^m } \right) ^{1/m} \end{aligned}$$

  (27)

  It is expected that the numerical value of the exponent “m” determined from Eq. (27) is not unique and depends on the permeability structure of the system. For example, the numerical values of the characteristic exponent “m” for all 85 layers of $10{\mathrm{th}}$ SPE model are shown in Fig. 6

• (B) The exponent “m” is inferred from equality of the permeability threshold value ($k_\mathrm{th}$) and the power law average between the geometric mean ($k_{\mathrm{g}-}$) of permeability values below the threshold (i.e., $k<k_\mathrm{th}$) and the geometric mean ($k_{\mathrm{g}+}$) of permeability values above the threshold ($k>k_\mathrm{th}$), i.e.,

  $$\begin{aligned} k_\mathrm{th} =k_{\mathrm{g}+}^m\cdot k_{\mathrm{g}-}^{1-m} \end{aligned}$$

  (28)

  Again it is expected that the numerical value of the exponent “m” determined from Eq. (28) depends on the permeability structure of the system. For example, the numerical values of the characteristic exponent “m” for all 85 layers of $10{\mathrm{th}}$ SPE model are shown in Fig. 7.

• (C) The exponent “m” is assumed to be a function of the ratio of the permeability threshold values of the real permeability map with given permeability probability density function and the permeability threshold value of the uncorrelated random field with the same permeability probability density function as the real one. In order to return to the typical behavior of models with spatially uncorrelated distributions (i.e., $m=0$ and $k_{\mathrm{est}} \approx k_\mathrm{th}$) we use the following functional form,

  $$\begin{aligned} m=1-\frac{k_{\mathrm{th}\text {-}\mathrm{rand}}}{k_\mathrm{th} } \end{aligned}$$

  (29)

Fig. 6

The numerical values of the characteristic exponent “m” inferred from Eq. (27) for all 85 layers of $10{\mathrm{th}}$ SPE model emphasizing the existence of different spatial distribution of permeability values in top 35 and lower 50 layers

Fig. 7

The numerical values of the characteristic exponent “m” inferred from Eq. (28) for all 85 layers of $10{\mathrm{th}}$ SPE model emphasizing the existence of different spatial distribution of permeability values in top 35 and lower 50 layers

4.5 A Characteristic Shape Factor Multiply by the Threshold Value

To estimate the effective permeability in this approach, we use an appropriately defined characteristic shape factor (SF) to multiply the threshold value ($k_{\mathrm{th}}$),

$$\begin{aligned} k_{\mathrm{eff}\text {-}\mathrm{est}} =\hbox {SF}\cdot k_\mathrm{th} \end{aligned}$$

(30)

This shape factor depends on real spatial pattern of the permeability field, with characteristics such as correlation length and anisotropy. There may be different methods to find a suitable shape factor (for instance, a shape factor can be developed by using the approximate streamline approach proposed by Begg and King 1985). In this paper we use the shape factor determined from the ratio of the strength of the connected cluster (defined by multiplying p by P) scaled by its corresponding fractal dimension with the strength of the connected cluster scaled by its corresponding fractal dimension appearing in the uncorrelated random field with the same permeability probability density function as the real one,

$$\begin{aligned} \mathrm{SF}=\frac{\left( {p\cdot P} \right) _{\mathrm{real}}^D }{\left( {p\cdot P} \right) _{\mathrm{rand}}^{1.89} } \end{aligned}$$

(31)

where the p and P stand respectively for the occupied fraction of high permeable cells and the connected fraction of high permeable cells at the threshold. The exponent D is the fractal dimension of the connected cluster in the real permeability map and 1.89 is the fractal dimension of uncorrelated random fields in two dimensions with the same permeability probability density function as the real one.

5 Results and Discussion

In this section, we present the results of the implementation of the presented approaches to estimate the effective permeability of different layers of $10{\mathrm{th}}$ SPE model and compare the estimations with the effective permeability determined from Eclipse.

5.1 The Threshold Value ($k_\mathrm{th}$)

The cross-plot of the permeability threshold value against the numerical effective permeability values calculated from Eclipse for the top and lower layers of $10{\mathrm{th}}$ SPE model are shown in Fig. 8.

Fig. 8

The cross-plot of the permeability threshold values against the numerical effective permeability values calculated from Eclipse for (left) the top and (right) the lower layers of $10{\mathrm{th}}$ SPE model

As can be seen, there is significant difference between the permeability thresholds values and the numerical effective permeability values calculated from Eclipse. We can quantify this by defining the normalized error as the deviation of the estimated effective permeability values ($k_{\mathrm{est}}$) by the methods proposed here and the value of the effective permeability computed by Eclipse ($K_{\mathrm{eclipse}}$) as,

$$\begin{aligned} \mathrm{Error}=\frac{k_{\mathrm{eclipse}} -k_{{\mathrm{eff}\text {-}\mathrm{est}}} }{k_{\mathrm{eclipse}} } \end{aligned}$$

(32)

The calculated normalized errors on the estimation of the effective permeability in this case for the top and lower layers of $10{\mathrm{th}}$ SPE model are shown in Fig. 9.

Fig. 9

The calculated normalized errors when we use the permeability threshold as an estimation of the effective permeability for (left) the top and (right) the lower layers of $10{\mathrm{th}}$ SPE model

In this method, the normalized error (and their variability among various layers) for the top and bottom layers of $10{\mathrm{th}}$ SPE model are $121\left( {\pm 99} \right)$ and $48\left( {\pm 17.5} \right) \,\%$ respectively. Hence, it is clear that we need alternative methods to improve the estimates. This shows that a single value of the threshold permeability of high conductance pathway ($K_\mathrm{th}$) cannot be the best expressed as an upscaling of the effective permeability.

Let consider the second method based on a weighted power average between the permeability threshold value and geometric mean of permeability distribution given by Eq. (22) with exponent $m=1$ to estimate the effective permeability. The cross-plot of the estimated effective permeability value (by using Eq. 22) against the effective permeability calculated by Eclipse for the top and lower layers of $10{\mathrm{th}}$ SPE model are shown in Fig. 10.

Fig. 10

The cross-plot of the estimated effective permeability values (when we used the weighted power average between the threshold value and geometric mean with $m=1$) against the numerical effective permeability values calculated from Eclipse for (left) the top and (right) the lower layers of $10{\mathrm{th}}$ SPE model

Moreover, the calculated normalized errors defined in Eq. (32) on the estimation of effective permeability for the top and lower layers of $10{\mathrm{th}}$ SPE model are shown in Fig. 11.

Fig. 11

The calculated normalized errors (when we used the weighted power average between the threshold value and geometric mean with $m=1$ as an estimation of effective permeability) for the top and lower layers of $10{\mathrm{th}}$ SPE model

In this method, the normalized errors (and their variability among various layers) for the top and bottom layers of $10{\mathrm{th}}$ SPE model are $1.5\left( {\pm 29} \right)$ and $4.5\left( {\pm 26} \right) \,\%$ respectively.

A similar analysis has been performed to estimate the effective permeability by using the other methods described in Sects. 4.2–4.5 (see “Appendix” for the detail results). A summary of the percentage of normalized errors obtained on the effective permeability estimations of these methods compared to the values calculated by Eclipse are shown in Table 1. It is noted that the estimation by using Eq. (12) supposed to be based on the critical path approximation (Hunt and Idriss 2009) gave $95\left( {\pm 4} \right)$ and $86\left( {\pm 6} \right) \,\%$ normalized errors for respectively the top and bottom layers of $10{\mathrm{th}}$ SPE model as compared to the estimates presented in Table 1.

Table 1 Summary of the percentage of normalized errors (and their variability in various layers) obtained on the effective permeability estimations using four methods presented in this work compared with the effective permeability values calculated by Eclipse

6 Conclusions

We presented four new methods of estimating the effective permeability of heterogeneous porous media by using concepts from percolation theory. We explain the rationale behind each method. The effective permeability has been analyzed on a rectangular geometry consistent with the geometry of $10{\mathrm{th}}$ SPE model, with a unidirectional gradient along an apparent axis of principal anisotropy direction. We examined those methods on different layers of $10{\mathrm{th}}$ SPE model to estimate the effective permeability of each layer and compared the results with the values calculated from the commercial flow simulators. We found that we can have reliable estimates of effective permeability for very heterogeneous models very quickly. We found that a power averaging method by using a moment from the permeability distribution (such as geometric mean) and the permeability threshold (i.e., showing the structure and topology) gives good estimates for the effective permeability. The result of this research opens insights on new methods in estimating physical properties of real heterogeneous porous media by using concepts from percolation theory. This approach can be extended to real 3D models and to consider the other flow regimes (e.g., radial).

Appendix

1.1 A Weighted Power Average Between the Threshold Value and Geometric Value of Permeability Distribution

Fig. 12

The cross-plot of the estimated effective permeability values (when we used the weighted power average between the threshold value and geometric value with $m=1.13$) against the numerical effective permeability values calculated from Eclipse for the top and lower layers of $10{\mathrm{th}}$ SPE model

Fig. 13

The calculated normalized errors (when we used the weighted power average between the threshold value and geometric value with $m=1.13$ as an estimation of effective permeability) for the top and lower layers of $10{\mathrm{th}}$ SPE model

• (A) We used the weighted power average between the threshold value and geometric value of permeability distribution given by Eq. (22) with exponent $m= 1.13$, the fractal dimension of minimal path in 2d percolation problems, to estimate the effective permeability. The cross-plot of the estimated effective permeability value against the effective permeability calculated from Eclipse for the top and lower layers of $10{\mathrm{th}}$ SPE model are shown in Fig. 12.

Moreover, the calculated normalized errors defined in Eq. (32) on the estimation of effective permeability for the top and lower layers of $10{\mathrm{th}}$ SPE model are shown in Figure 13.

Fig. 14

The cross-plot of the estimated effective permeability values (when we used the weighted power average between the threshold value and geometric value with $m=1.89/D$) against the numerical effective permeability values calculated from Eclipse for the top and lower layers of $10{\mathrm{th}}$ SPE model

Fig. 15

The calculated normalized errors (when we used the weighted power average between the threshold value and geometric value with $m=1.89/D$ as an estimation of effective permeability) for the top and lower layers of $10{\mathrm{th}}$ SPE model

In this method, the normalized error (and their variability among various layers) for the top and bottom layers of $10{\mathrm{th}}$ SPE model are $6.2\left( {\pm 29.7} \right)$ and $1.7\left( {\pm 27.9} \right) \,\%$ respectively.

• (B) We used the weighted power average between the threshold value and geometric value of permeability distribution given by Eq. (22) with exponent $m=\frac{1.89}{D}$ to estimate the effective permeability. The cross-plot of the estimated effective permeability value against effective permeability calculated from Eclipse for two layers are shown in Fig. 14.

Moreover, the calculated normalized errors defined in Eq. (32) on the estimation of effective permeability for the top and lower layers of $10{\mathrm{th}}$ SPE model are shown in Fig. 15.

Fig. 16

The cross-plot of the estimated effective permeability values [when we used the power law function of occupancy probability scaled by the permeability threshold value with exponent m from Eq. (27)] against the numerical effective permeability values calculated from Eclipse for the top and lower layers of $10{\mathrm{th}}$ SPE model

Fig. 17

The calculated normalized errors (when we used the power law function of occupancy probability scaled by the permeability threshold value with exponent m from Eq. (27) as an estimation of effective permeability) for the top and lower layers of $10{\mathrm{th}}$ SPE model

Fig. 18

The cross-plot of the estimated effective permeability values [when we used the power law function of occupancy probability scaled by the permeability threshold value with exponent m from Eq. (28)] against the numerical effective permeability values calculated from Eclipse for the top and lower layers of $10{\mathrm{th}}$ SPE model

Fig. 19

The calculated normalized errors (when we used the power law function of occupancy probability scaled by the permeability threshold value with exponent m from Eq. (28) as an estimation of effective permeability) for the top and lower layers of $10{\mathrm{th}}$ SPE model

In this method, the normalized error (and their variability among various layers) for the top and bottom layers of $10{\mathrm{th}}$ SPE model are $1\left( {\pm 29} \right)$ and $1.3\left( {\pm 28} \right) \,\%$ respectively.

1.2 A Power Law Function of Occupancy Probability (p) Scaled by the Permeability Threshold Value ($K_\mathrm{th}$)

• (A) We used the power law function of occupancy probability scaled by the permeability threshold value given in Eq. (26) with exponent m obtained from power average Eq. (27) using percolation subnetworks statistics to estimate the effective permeability. The cross-plot of the estimated effective permeability value against effective permeability calculated from Eclipse for two layers are shown in Fig. 16.

Fig. 20

The cross-plot of the estimated effective permeability values (when we used the power law function of occupancy probability scaled by the permeability threshold value with exponent m dependent on the ratio of two threshold values) against the numerical effective permeability values calculated from Eclipse for the top and lower layers of $10{\mathrm{th}}$ SPE model

Fig. 21

The calculated normalized errors (when we used the power law function of occupancy probability scaled by the permeability threshold value with exponent m dependent on the ratio of two threshold values as an estimation of effective permeability) for the top and lower layers of $10{\mathrm{th}}$ SPE model

Fig. 22

The cross-plot of the estimated effective permeability values [when we used Eq. (30) with its characteristics shape factor] against the numerical effective permeability values calculated from Eclipse for the top and lower layers of $10{\mathrm{th}}$ SPE model

Fig. 23

The calculated normalized errors (when we used Eq. (30) with its characteristics shape factor) for the top and lower layers of $10{\mathrm{th}}$ SPE model

Moreover, the calculated normalized errors defined in Eq. (32) on the estimation of effective permeability for the top and lower layers of $10{\mathrm{th}}$ SPE model are shown in Fig. 17.

In this method, the normalized error (and their variability among various layers) for the top and bottom layers of $10{\mathrm{th}}$ SPE model are $29\left( {\pm 27} \right)$ and $31\left( {\pm 41} \right) \,\%$ respectively.

• (B) We used the power law function of occupancy probability scaled by the threshold value given in Eq. (26) with exponent m obtained from power law average Eq. (28) using percolation subnetworks statistics to estimate the effective permeability. The cross-plot of the estimated effective permeability value against effective permeability calculated from Eclipse for two layers are shown in Fig. 18.

Moreover, the calculated normalized errors defined in Eq. (32) on the estimation of effective permeability for the top and lower layers of $10{\mathrm{th}}$ SPE model are shown in Fig. 19.

In this method, the normalized error (and their variability among various layers) for the top and bottom layers of $10{\mathrm{th}}$ SPE model are $52.5\left( {\pm 17} \right)$ and $6.5\left( {\pm 32} \right) \,\%$ respectively.

• (C) We used the power law function of occupancy probability scaled by the threshold value given in Eq. (26) with exponent m dependent on the ratio of two threshold values in Eq. (29) to estimate the effective permeability. The cross-plot of the estimated effective permeability value against effective permeability calculated from Eclipse for two layers are shown in Fig. 20.

Moreover, the calculated normalized errors defined in Eq. (32) on the estimation of effective permeability for the top and lower layers of $10{\mathrm{th}}$ SPE model are shown in Fig. 21.

In this method, the normalized error (and their variability among various layers) for the top and bottom layers of $10{\mathrm{th}}$ SPE model are $22\left( {\pm 26} \right)$ and $12\left( {\pm 23} \right) \,\%$ respectively.

1.3 A Characteristic Shape Factor Multiply by the Threshold Value

We use Eq. (30) with the characteristics shape factor given by Eq. (31) to estimate the effective permeability. The cross-plot of the estimated effective permeability value against effective permeability calculated from Eclipse for two layers are shown in Fig. 22.

Moreover, the calculated normalized errors defined in Eq. (32) on the estimation of effective permeability for the top and lower layers of $10{\mathrm{th}}$ SPE model are shown in Fig. 23.

In this method, the normalized error (and their variability among various layers) for the top and bottom layers of $10{\mathrm{th}}$ SPE model are $6.5\left( {\pm 25} \right)$ and $10\left( {\pm 32} \right) \,\%$ respectively.