Counting distinctions: on the conceptual foundations of Shannon’s information theory

Abstract

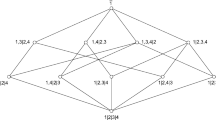
Categorical logic has shown that modern logic is essentially the logic of subsets (or “subobjects”). In “subset logic,” predicates are modeled as subsets of a universe and a predicate applies to an individual if the individual is in the subset. Partitions are dual to subsets so there is a dual logic of partitions where a “distinction” [an ordered pair of distinct elements (u, u′) from the universe U] is dual to an “element”. A predicate modeled by a partition π on U would apply to a distinction if the pair of elements was distinguished by the partition π, i.e., if u and u′ were in different blocks of π. Subset logic leads to finite probability theory by taking the (Laplacian) probability as the normalized size of each subset-event of a finite universe. The analogous step in the logic of partitions is to assign to a partition the number of distinctions made by a partition normalized by the total number of ordered |U|² pairs from the finite universe. That yields a notion of “logical entropy” for partitions and a “logical information theory.” The logical theory directly counts the (normalized) number of distinctions in a partition while Shannon’s theory gives the average number of binary partitions needed to make those same distinctions. Thus the logical theory is seen as providing a conceptual underpinning for Shannon’s theory based on the logical notion of “distinctions.”