Skip to main content
SpringerLink
Log in

Shock Acceleration of Ions in the Heliosphere

  • Published:
Space Science Reviews Aims and scope Submit manuscript

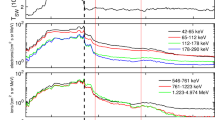
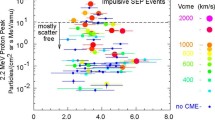
Abstract

Energetic particles constitute an important component of the heliospheric plasma environment. They range from solar energetic particles in the inner heliosphere to the anomalous cosmic rays accelerated at the interface of the heliosphere with the local interstellar medium. Although stochastic acceleration by fluctuating electric fields and processes associated with magnetic reconnection may account for some of the particle populations, the majority are accelerated by the variety of shock waves present in the solar wind. This review focuses on “gradual” solar energetic particle (SEP) events including their energetic storm particle (ESP) phase, which is observed if and when an associated shock wave passes Earth. Gradual SEP events are the intense long-duration events responsible for most space weather disturbances of Earth’s magnetosphere and upper atmosphere. The major characteristics of gradual SEP events are first described including their association with shocks and coronal mass ejections (CMEs), their ion composition, and their energy spectra. In the context of acceleration mechanisms in general, the acceleration mechanism responsible for SEP events, diffusive shock acceleration, is then described in some detail including its predictions for a planar stationary shock, shock modification by the energetic particles, and wave excitation by the accelerating ions. Finally, some complexities of shock acceleration are addressed, which affect the predictive ability of the theory. These include the role of temporal and spatial variations, the distinction between the plasma and wave compression ratios at the shock, the injection of thermal plasma at the shock into the process of shock acceleration, and the nonlinear evolution of ion-excited waves in the vicinity of the shock.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

References

  • O. Adriani et al., Observations of the 2006 December 13 and 14 solar particle events in the 80 MeVn-1-3 GeVn-1 range from space with the PAMELA detector. Astrophys. J. 742, 102 (2011)

    Article  ADS  Google Scholar 

  • W.I. Axford, Acceleration of cosmic rays by shock waves, in Proc. Int. Conf. Cosmic Rays 17th, vol. 12 (1981), p. 155

    Google Scholar 

  • W.I. Axford, E. Leer, G. Skadron, The acceleration of cosmic rays by shock waves, in Proc. Int. Conf. Cosmic Rays 15th, vol. 11, (1977), p. 132

    Google Scholar 

  • D. Band et al., Batse observations of gamma ray burst spectra. 1—Spectral diversity. Astrophys. J. 413, 281 (1993)

    Article  ADS  Google Scholar 

  • A.R. Bell, The acceleration of cosmic rays in shock fronts. Mon. Not. R. Astron. Soc. 182, 147 (1978)

    ADS  Google Scholar 

  • A.R. Bell, Turbulent amplification of magnetic field and diffusive shock acceleration of cosmic rays. Mon. Not. R. Astron. Soc. 353, 550 (2004)

    Article  ADS  Google Scholar 

  • A.R. Bell, S.G. Lucek, Cosmic ray acceleration to very high energy through the non-linear amplification by cosmic rays of the seed magnetic field. Mon. Not. R. Astron. Soc. 321, 433 (2001)

    Article  ADS  Google Scholar 

  • R.D. Blandford, J.P. Ostriker, Particle acceleration by astrophysical shocks. Astrophys. J. 221, L29 (1978)

    Article  ADS  Google Scholar 

  • P. Bochsler, E. Möbius, Energetic neutral atoms: an additional source for heliospheric pickup ions. Astrophys. J. 721, L6 (2010)

    Article  ADS  Google Scholar 

  • T.J. Bogdan, M.A. Lee, P. Schneider, Coupled quasi-linear wave damping and stochastic acceleration of pickup ions in the solar wind. J. Geophys. Res. 96, 161 (1991)

    Article  ADS  Google Scholar 

  • C. Bonifazi, G. Moreno, Reflected and diffuse ions backstreaming from the Earth’s bow shock, 2. Origin. J. Geophys. Res. 86, 4405 (1981)

    Article  ADS  Google Scholar 

  • H.H. Breneman, E.C. Stone, Solar coronal and photospheric abundances from solar energetic particle measurements. Astrophys. J. 299, L57 (1985)

    Article  ADS  Google Scholar 

  • D. Burgess, E. Möbius, M. Scholer, Ion acceleration at the Earth’s bow shock. Space Sci. Rev. (2012, this issue). doi:10.1007/s11214-012-9901-5

  • M. Bzowski, M. Krolikowska, Are the sungrazing comets the inner source of pickup ions and energetic neutral atoms? Astron. Astrophys. 435, 723 (2005)

    Article  ADS  Google Scholar 

  • H.V. Cane, T.T. von Rosenvinge, C.M.S. Cohen, R.A. Mewaldt, Two components in major solar particle events. Geophys. Res. Lett. 30, 8017 (2003). doi:10.1029/2002GL016580

    Article  ADS  Google Scholar 

  • H.V. Cane, R.A. Mewaldt, C.M.S. Cohen, T.T. von Rosenvinge, Role of flares and shocks in determining solar energetic particle abundances. J. Geophys. Res. 111, A06S90 (2006). doi:10.1029/2005JA011071

    Article  ADS  Google Scholar 

  • P.J. Cargill, L. Vlahos, G. Baumann, J.F. Drake, A. Nordlund, Current fragmentation and particle acceleration in solar flares. Space Sci. Rev. (2012, this issue). doi:10.1007/s11214-012-9888-y

  • S.V. Chalov, H.J. Fahr, Energetic particles from the outer heliosphere appearing as a secondary pick-up ion component. Astron. Astrophys. 401, L1 (2003)

    Article  ADS  Google Scholar 

  • C.M.S. Cohen et al., New observations of heavy-ion-rich solar particle events from ACE. Geophys. Res. Lett. 26, 2697 (1999a)

    Article  ADS  Google Scholar 

  • C.M.S. Cohen et al., Inferred charge states of high energy solar particles from the solar isotope spectrometer on ACE. Geophys. Res. Lett. 26, 149 (1999b)

    Article  ADS  Google Scholar 

  • C.M.S. Cohen et al., Heavy ion abundances and spectra from the large solar energetic particle events of October-November 2003. J. Geophys. Res. 110, A09S16 (2005). doi:10.1029/2005JA011004

    Article  ADS  Google Scholar 

  • R.B. Decker, The modulation of low-energy proton distributions by propagating interplanetary shock waves: a numerical simulation. J. Geophys. Res. 86, 4537 (1981)

    Article  ADS  Google Scholar 

  • M.I. Desai et al., Spectral properties of heavy ions associated with the passage of interplanetary shocks at 1 AU. Astrophys. J. 611, 1156 (2004)

    Article  ADS  Google Scholar 

  • M.I. Desai et al., Heavy-ion elemental abundances in large solar energetic particle events and their implications for the seed population. Astrophys. J. 649, 470 (2006a)

    Article  ADS  Google Scholar 

  • M.I. Desai, G.M. Mason, J.E. Mazur, J.R. Dwyer, Solar cycle variations in the composition of the suprathermal heavy-ion population near 1 AU. Astrophys. J. 645, L81 (2006b)

    Article  ADS  Google Scholar 

  • L.O’C. Drury, An introduction to the theory of diffusive shock acceleration of energetic particles in tenuous plasmas. Rep. Prog. Phys. 46, 973 (1983)

    Article  ADS  Google Scholar 

  • L.O’C. Drury, W.I. Axford, D. Summers, Particle acceleration in modified shocks. Mon. Not. R. Astron. Soc. 198, 833 (1982)

    ADS  MATH  Google Scholar 

  • J.A. Earl, The effect of adiabatic focusing upon charged particle propagation in random magnetic fields. Astrophys. J. 205, 900 (1976)

    Article  ADS  Google Scholar 

  • D. Eichler, A cosmic ray mediated shock in the solar system. Astrophys. J. 247, 1089 (1981)

    Article  ADS  Google Scholar 

  • D.C. Ellison, R. Ramaty, Shock acceleration of electrons and ions in solar flares. Astrophys. J. 298, 400 (1985)

    Article  ADS  Google Scholar 

  • A.G. Emslie et al., Energy partition in two solar flare/CME events. J. Geophys. Res. 109, A10104 (2004). doi:10.1029/2004JA010571

    Article  ADS  Google Scholar 

  • A.G. Emslie, B.R. Dennis, G.D. Holman, H.S. Hudson, Refinements to flare energy estimates: a followup to “Energy partition in two solar flare/CME events” by A.G. Emslie et al. J. Geophys. Res. 110, A11103 (2005). doi:10.1029/2005JA011305

    Article  ADS  Google Scholar 

  • A. Falcone et al., Observation of GeV solar energetic particles from the 1997 November 6 event using Milagrito. Astrophys. J. 588, 557 (2003)

    Article  ADS  Google Scholar 

  • E. Fermi, On the origin of the cosmic radiation. Phys. Rev. 75, 1169 (1949)

    Article  ADS  MATH  Google Scholar 

  • E. Fermi, Galactic magnetic fields and the origin of cosmic radiation. Astrophys. J. 119, 1 (1954)

    Article  ADS  Google Scholar 

  • L.A. Fisk, G. Gloeckler, Acceleration of suprathermal tails in the solar wind. Astrophys. J. 686, 1466 (2008)

    Article  ADS  Google Scholar 

  • L.A. Fisk, G. Gloeckler, Particle acceleration in the heliosphere: implications for astrophysics. Space Sci. Rev. (2012, this issue). doi:10.1007/s11214-012-9899-8

  • L.A. Fisk, M.A. Lee, Shock acceleration of energetic particles in corotating interaction regions in the solar wind. Astrophys. J. 237, 620 (1980)

    Article  ADS  Google Scholar 

  • V. Florinski, R.B. Decker, J.A. le Roux, G.P. Zank, An energetic-particle-mediated termination shock observed by Voyager 2. Geophys. Res. Lett. 36, L12101 (2009). doi:10.1029/2009GL038423

    Article  ADS  Google Scholar 

  • S.E. Forbush, Three unusual cosmic-ray increases possibly due to charged particles from the Sun. Phys. Rev. 70, 771 (1946)

    Article  ADS  Google Scholar 

  • M.A. Forman, L.O’C. Drury, Time dependent shock acceleration: approximations and exact solutions, in Proc. Int. Conf. Cosmic Rays 18th, vol. 2 (1983), p. 267

    Google Scholar 

  • J. Geiss, G. Gloeckler, L.A. Fisk, R. von Steiger, C+ pickup ions in the heliosphere and their origin. J. Geophys. Res. 100, 23373 (1995)

    Article  ADS  Google Scholar 

  • J. Giacalone, The efficient acceleration of thermal protons by perpendicular shocks. Astrophys. J. 628, L37 (2005)

    Article  ADS  Google Scholar 

  • J. Giacalone, J.R. Jokipii, The transport of cosmic rays across a turbulent magnetic field. Astrophys. J. 520, 204 (1999)

    Article  ADS  Google Scholar 

  • J. Giacalone, J.R. Jokipii, Magnetic field amplification by shocks in turbulent fluids. Astrophys. J. 663, L41 (2007)

    Article  ADS  Google Scholar 

  • J. Giacalone, J.R. Jokipii, Suprathermal ions associated with strong interplanetary shocks, in Particle Acceleration and Transport. AIP Conf. Proc., vol. 1436 (AIP, New York, 2012), p. 130

    Google Scholar 

  • J. Giacalone, M. Neugebauer, The energy spectrum of energetic particles downstream of turbulent collisionless shocks. Astrophys. J. 673, 629 (2008)

    Article  ADS  Google Scholar 

  • J. Giacalone, J.F. Drake, J.R. Jokipii, The acceleration mechanism of anomalous cosmic rays. Space Sci. Rev. (2012, this issue). doi:10.1007/s11214-012-9915-z

  • G. Gloeckler et al., Acceleration of interstellar pickup ions in the disturbed solar wind observed on Ulysses. J. Geophys. Res. 99, 17637 (1994)

    Article  ADS  Google Scholar 

  • G. Gloeckler et al., Interception of comet Hyakutake’s ion tail at a distance of 500 million kilometres. Nature 404, 576 (2000a)

    Article  ADS  Google Scholar 

  • G. Gloeckler, L.A. Fisk, J. Geiss, N.A. Schwadron, T.H. Zurbuchen, Elemental composition of the inner source pickup ions. J. Geophys. Res. 105, 7459 (2000b)

    Article  ADS  Google Scholar 

  • G. Gloeckler et al., Sources, injection and acceleration of heliospheric ion populations, in Acceleration and Transport of Energetic Particles Observed the Heliosphere: ACE 2000 Symposium, ed. by R.A. Mewaldt et al., AIP Conference Proceedings, vol. 528 (AIP, New York, 2000c), p. 221

    Google Scholar 

  • N. Gopalswamy, Coronal mass ejections of Solar Cycle 23. J. Astrophys. Astron. 27, 243 (2006)

    Article  ADS  Google Scholar 

  • N. Gopalswamy et al., Interacting coronal mass ejections and solar energetic particles. Astrophys. J. 572, L103 (2002)

    Article  ADS  Google Scholar 

  • N. Gopalswamy, S. Yashiro, S. Krucker, G. Stenborg, R.A. Howard, Intensity variation of large solar energetic particle events associated with coronal mass ejections. J. Geophys. Res. 109, A12105 (2004). doi:10.1029/2004JA010602

    Article  ADS  Google Scholar 

  • N. Gopalswamy, H. Xie, S. Yashiro, S. Akiyama, P. Mäkelä, I.G. Usoskin, Properties of ground level enhancement events and the associated solar eruptions during Solar Cycle 23. Space Sci. Rev. (2012). doi:10.1007/s11214-012-9890-4

    Google Scholar 

  • B.E. Gordon, M.A. Lee, E. Möbius, K.J. Trattner, Coupled hydromagnetic wave excitation and ion acceleration at interplanetary traveling shocks and Earth’s bow shock revisited. J. Geophys. Res. 104, 28263 (1999)

    Article  ADS  Google Scholar 

  • T. Hada, C.F. Kennel, T. Terasawa, Excitation of compressional waves and the formation of shocklets in the Earth’s foreshock. J. Geophys. Res. 92, 4423 (1987)

    Article  ADS  Google Scholar 

  • E.A. Helder, J. Vink, A.M. Bykov, Y. Ohira, J.C. Raymond, R. Terrier, Observational signatures of particle acceleration in supernova remnants. Space Sci. Rev. (2012, this issue). doi:10.1007/s11214-012-9919-8

  • M.M. Hoppe, C.T. Russell, L.A. Frank, T.E. Eastman, E.W. Greenstadt, Upstream hydromagnetic waves and their association with backstreaming ion populations—ISEE 1 and 2 observations. J. Geophys. Res. 86, 4471 (1981)

    Article  ADS  Google Scholar 

  • P.D. Hudson, Reflection of charged particles by plasma shocks. Mon. Not. R. Astron. Soc. 131, 23 (1965)

    ADS  Google Scholar 

  • P.A. Isenberg, A hemispherical model of anisotropic interstellar pickup ions. J. Geophys. Res. 102, 4719 (1997)

    Article  ADS  Google Scholar 

  • J.R. Jokipii, Propagation of cosmic rays in the solar wind. Rev. Geophys. Space Phys. 9, 27 (1971)

    Article  ADS  Google Scholar 

  • J.R. Jokipii, Rate of energy gain and maximum energy in diffusive shock acceleration. Astrophys. J. 313, 842 (1987)

    Article  ADS  Google Scholar 

  • J.R. Jokipii, M.A. Lee, Compression acceleration in astrophysical plasmas and the production of f(v)∝v −5 spectra in the heliosphere. Astrophys. J. 713, 475 (2010)

    Article  ADS  Google Scholar 

  • S.W. Kahler, The correlation between solar energetic particle peak intensities and speeds of coronal mass ejections: effects of ambient particle intensities and energy spectra. J. Geophys. Res. 106, 20947 (2001)

    Article  ADS  Google Scholar 

  • S.W. Kahler et al., Associations between coronal mass ejections and solar energetic proton events. J. Geophys. Res. 89, 9683 (1984)

    Article  ADS  Google Scholar 

  • C.F. Kennel, F.V. Coroniti, F.L. Scarf, W.A. Livesey, C.T. Russell, E.J. Smith, A test of Lee’s quasi-linear theory of ion acceleration by interplanetary traveling shocks. J. Geophys. Res. 91, 11917 (1986)

    Article  ADS  Google Scholar 

  • B. Klecker, E. Möbius, M.A. Popecki, Ionic charge states of solar energetic particles: a clue to the source. Space Sci. Rev. 130, 273 (2007)

    Article  ADS  Google Scholar 

  • J. Kota, Anomalous cosmic rays at a blunt termination shock, in Proc. Int. Conf. Cosmic Rays 30th, vol. 1 (2008), p. 853

    Google Scholar 

  • G.F. Krymsky, A regular mechanism for the acceleration of charged particles on the front of a shock wave. Dokl. Akad. Nauk SSSR 234, 1306 (1977)

    ADS  Google Scholar 

  • H. Kucharek et al., On the source and acceleration of energetic He+: a long-term observation with ACE/SEPICA. J. Geophys. Res. 108(A10), 8040 (2003). doi:10.1029/2003JA009938

    Article  Google Scholar 

  • J. Kunches (2005). http://umbra.nascom.nasa.gov/SEP/

  • D. Lario, G.C. Ho, R.B. Decker, E.C. Roelof, M.I. Desai, C.W. Smith, ACE observations of energetic particles associated with transient interplanetary shocks, in Solar Wind Ten. AIP Conference Proceedings, vol. 679 (AIP, New York, 2003) 640

    Google Scholar 

  • M.A. Lee, Coupled hydromagnetic wave excitation and ion acceleration upstream of the Earth’s bow shock. J. Geophys. Res. 87, 5063 (1982)

    Article  ADS  Google Scholar 

  • M.A. Lee, Coupled hydromagnetic wave excitation and ion acceleration at interplanetary traveling shocks. J. Geophys. Res. 88, 6109 (1983)

    Article  ADS  Google Scholar 

  • M.A. Lee, Coupled hydromagnetic wave excitation and ion acceleration at an evolving coronal/interplanetary shock. Astrophys. J. Suppl. 158, 38 (2005)

    Article  ADS  Google Scholar 

  • M.A. Lee, H.J. Völk, Hydromagnetic waves and cosmic ray diffusion theory. Astrophys. J. 198, 485 (1975)

    Article  ADS  Google Scholar 

  • R.A. Leske et al., Solar isotopic composition as determined using solar energetic particles. Space Sci. Rev. 130, 195 (2007). doi:10.1007/s11214-007-9185-3

    Article  ADS  Google Scholar 

  • G. Li, G.P. Zank, Mixed particle acceleration at CME-driven shocks and flares. Geophys. Res. Lett. 32, L02101 (2005a). doi:10.1029/2004GL021250

    Article  Google Scholar 

  • G. Li, G.P. Zank, Multiple CMEs and large gradual SEP events, in Proc. Int. Conf. Cosmic Rays 29th, vol. 1 (2005b), p. 173

    Google Scholar 

  • G. Li, G.P. Zank, W.K.M. Rice, Acceleration and transport of heavy ions at coronal mass ejection-driven shocks. J. Geophys. Res. 110, A06104 (2005). doi:10.1029/2004JA010600

    Article  ADS  Google Scholar 

  • G. Li et al., Shock geometry and spectral breaks in large SEP events. Astrophys. J. 702, 998 (2009)

    Article  ADS  Google Scholar 

  • G. Li, R. Moore, R.A. Mewaldt, L. Zhao, A.W. Labrador, A twin-CME scenario for ground level enhancement events. Space Sci. Rev. (2012). doi:10.1007/s11214-011-9823-7

    Google Scholar 

  • R.P. Lin, Energy release and particle acceleration in flares: summary and future prospects. Space Sci. Rev. 159, 421 (2011). doi:10.1007/s11214-011-9801-0

    Article  ADS  Google Scholar 

  • C. Lopate, Fifty years of ground level solar particle event observations, in Solar Eruptions and Energetic Particles, ed. by N. Gopalswamy, R.A. Mewaldt, J. Torsti, AGU Monograph Series (AGU, Washington, 2006), p. 283

    Chapter  Google Scholar 

  • E.A. Lucek, T.S. Horbury, I. Dandouras, H. Reme, Cluster observations of the Earth’s quasi-parallel bow shock. J. Geophys. Res. 113, A07S02 (2008). doi:10.1029/2007JA012756

    Article  ADS  Google Scholar 

  • G. Mann, A. Klassen, H. Aurass, H.-T. Classen, Formation and development of shock waves in the solar corona and the near-Sun interplanetary space. Astron. Astrophys. 400, 329 (2003)

    Article  ADS  Google Scholar 

  • G.M. Mason et al., Particle acceleration and sources in the November 1997 solar energetic particle events. Geophys. Res. Lett. 26, 141 (1999a)

    Article  ADS  Google Scholar 

  • G.M. Mason, J.E. Mazur, J.R. Dwyer, 3He enhancements in large solar energetic particle events. Astrophys. J. 525, L133 (1999b)

    Article  ADS  Google Scholar 

  • G.M. Mason et al., Abundances of heavy and ultraheavy ions in 3He-rich solar flares. Astrophys. J. 606, 555 (2004)

    Article  ADS  Google Scholar 

  • S. Masson et al., Acceleration of relativistic protons during the 20 January 2005 flare and CME. Sol. Phys. 257, 305 (2009)

    Article  ADS  Google Scholar 

  • J.E. Mazur, G.M. Mason, M.D. Looper, R.A. Leske, R.A. Mewaldt, Charge states of solar energetic particles using the geomagnetic cutoff technique: SAMPEX measurements in the 6 November 1997 solar particle event. Geophys. Res. Lett. 26, 173 (1999)

    Article  ADS  Google Scholar 

  • D.J. McComas, N.A. Schwadron, An explanation of the Voyager paradox: particle acceleration at a blunt termination shock. Geophys. Res. Lett. 33, L04102 (2006). doi:10.1029/2005GL025437

    Article  Google Scholar 

  • K.G. McCracken, H. Moraal, P.H. Stoker, Investigation of the multiple-component structure of the 20 January 2005 cosmic ray ground level enhancement. J. Geophys. Res. 113, A12101 (2008). doi:10.1029/2007JA012829

    Article  ADS  Google Scholar 

  • R.B. McKibben, Azimuthal propogation of low-energy solar-flare protons as observed from spacecraft very widely separated in solar azimuth. J. Geophys. Res. 77, 3957 (1972)

    Article  ADS  Google Scholar 

  • R.A. Mewaldt, Solar energetic particle composition, energy spectra, and space weather. Space Sci. Rev. 124, 303 (2007). doi:10.1007/s11214-006-9091-0

    Article  ADS  Google Scholar 

  • R.A. Mewaldt et al. (eds.), Acceleration and Transport of Energetic Particles Observed in the Heliosphere: ACE 2000 Symposium. AIP Conference Proceedings, vol. 528 (2000). Cover picture

    Google Scholar 

  • R.A. Mewaldt et al., Proton, helium, and electron spectra during the large solar particle events of October-November 2003. J. Geophys. Res. 110, A09S18 (2005). doi:10.1029/2005JA011038

    Article  ADS  Google Scholar 

  • R.A. Mewaldt, C.M.S. Cohen, G.M. Mason, The source material for large solar energetic particle events, in Solar Eruptions and Energetic Particles, ed. by N. Gopalswamy, R.A. Mewaldt, J. Torsti, AGU Monograph Series, vol. 165 (2006), p. 115

    Chapter  Google Scholar 

  • R.A. Mewaldt et al., On the differences in composition between solar energetic particles and solar wind. Space Sci. Rev. 130, 207 (2007)

    Article  ADS  Google Scholar 

  • R.A. Mewaldt et al., How efficient are coronal mass ejections at accelerating solar energetic particles? in Particle Acceleration and Transport in the Heliosphere and Beyond. AIP Conference Proceedings, vol. 1039 (2008), p. 111

    Google Scholar 

  • R.A. Mewaldt et al., STEREO observations of energetic neutral hydrogen atoms during the 2006 December 5 solar flare. Astrophys. J. 693, L11 (2009)

    Article  ADS  Google Scholar 

  • R.A. Mewaldt et al., Observations and interpretations of energetic neutral hydrogen atoms from the December 5, 2006 solar event, in Twelfth International Solar Wind Conference. AIP Conference Proceedings, vol. 1216 (AIP, New York, 2010), p. 592

    Google Scholar 

  • R.A. Mewaldt et al., Energy spectra, composition, and other properties of ground-level events during Solar Cycle 23. Space Sci. Rev. (2012). doi:10.1007/s11214-012-9884-2

    Google Scholar 

  • P.M. Morse, H. Feshbach, Methods of Theoretical Physics (McGraw-Hill, New York, 1953), pp. 865–869

    MATH  Google Scholar 

  • M. Neugebauer, J. Giacalone, Multispacecraft observations of interplanetary shocks: nonplanarity and energetic particles. J. Geophys. Res. 110, A12106 (2005). doi:10.1029/2005JA011380

    Article  ADS  Google Scholar 

  • M. Neugebauer et al., Encounter of the Ulysses spacecraft with the ion tail of Comet McNaught. Astrophys. J. 667, 1262 (2007)

    Article  ADS  Google Scholar 

  • C.K. Ng, D.V. Reames, Focused interplanetary transport of approximately 1 MeV solar energetic protons through self-generated Alfvén waves. Astrophys. J. 424, 1032 (1994)

    Article  ADS  Google Scholar 

  • C.K. Ng, D.V. Reames, A.J. Tylka, Effect of proton-amplified waves on the evolution of solar energetic particle composition in gradual events. Geophys. Res. Lett. 26, 2145 (1999)

    Article  ADS  Google Scholar 

  • V. Ontiveros, A. Vourlidas, Quantitative measurements of coronal mass ejection-driven shocks from LASCO observations. Astrophys. J. 693, 267 (2009)

    Article  ADS  Google Scholar 

  • E.N. Parker, The passage of energetic charged particles through interplanetary space. Planet. Space Sci. 13, 9 (1965)

    Article  ADS  Google Scholar 

  • G. Paschmann et al., Characteristics of reflected and diffuse ions upstream from the Earth’s bow shock. J. Geophys. Res. 86, 4355 (1981)

    Article  ADS  Google Scholar 

  • V.S. Ptuskin, Cosmic-ray acceleration by long-wave turbulence. Pis’ma Astron. Zh. 14, 599 (1988)

    ADS  Google Scholar 

  • V.S. Ptuskin, Propagation, confinement models, and large-scale dynamical effects of galactic cosmic rays. Space Sci. Rev. 99, 281 (2001)

    Article  ADS  Google Scholar 

  • K.R. Pyle, J.A. Simpson, A. Barnes, J.D. Mihalov, Shock acceleration of nuclei and electrons in the heliosphere beyond 24 AU. Astrophys. J. 282, 107 (1984)

    Article  ADS  Google Scholar 

  • J.C. Raymond, S. Krucker, R.P. Lin, V. Petrosian, Observational aspects of particle acceleration in large solar flares. Space Sci. Rev. (2012, this issue). doi:10.1007/s11214-012-9897-x

  • D.V. Reames, Acceleration of energetic particles by shock waves from large solar flares. Astrophys. J. 358, L63 (1990)

    Article  ADS  Google Scholar 

  • D.V. Reames, Coronal abundances determined from energetic particles. Adv. Space Res. 15, 41 (1995)

    Article  ADS  Google Scholar 

  • D.V. Reames, Particle acceleration by CME-driven shock waves, in Proc. Int. Conf. Cosmic Rays 26th. AIP Conference Proceedings, vol. 516 (AIP, New York, 2000), pp. 289–300

    Google Scholar 

  • D.V. Reames, C.K. Ng, Streaming-limited intensities of solar energetic particles. Astrophys. J. 504, 1002 (1998)

    Article  ADS  Google Scholar 

  • D.V. Reames, C.K. Ng, Streaming-limited intensities of solar energetic particles on the intensity plateau. Astrophys. J. 723, 1286 (2010)

    Article  ADS  Google Scholar 

  • D.V. Reames et al., Energy spectra of ions accelerated in impulsive and gradual solar events. Astrophys. J. 483, 515 (1997a)

    Article  ADS  Google Scholar 

  • D.V. Reames, S.W. Kahler, C.K. Ng, Spatial and temporal invariance in the spectra of energetic particles in gradual solar events. Astrophys. J. 491, 414 (1997b)

    Article  ADS  Google Scholar 

  • D.V. Reames et al., Late-phase acceleration of energetic ions in corotating interaction regions. Geophys. Res. Lett. 24, 2917 (1997c)

    Article  ADS  Google Scholar 

  • E.C. Roelof, Propagation of solar cosmic rays in the interplanetary magnetic field, in Lectures in High-Energy Astrophysics, ed. by H. Ögelman, J.R. Wayland, NASA SP-199 (NASA, Washington, 1969), p. 111

    Google Scholar 

  • E.T. Sarris, J.A. Van Allen, Effects of interplanetary shock waves on energetic charged particles. J. Geophys. Res. 79, 4157 (1974)

    Article  ADS  Google Scholar 

  • K.M. Schure, A.R. Bell, L. O’C. Drury, A.M. Bykov, Diffusive shock acceleration and magnetic field amplification. Space Sci. Rev. (2012, this issue). doi:10.1007/s11214-012-9871-7

  • N.A. Schwadron, D.J. McComas, Pickup ions from energetic neutral atoms. Astrophys. J. 712, L157 (2010)

    Article  ADS  Google Scholar 

  • N.A. Schwadron, M.A. Lee, D.J. McComas, Diffusive acceleration at the blunt termination shock. Astrophys. J. 675, 1584 (2008)

    Article  ADS  Google Scholar 

  • S.J. Schwartz, D. Burgess, Quasi-parallel shocks—a patchwork of three-dimensional structures. Geophys. Res. Lett. 18, 373 (1991)

    Article  ADS  Google Scholar 

  • E.C. Stone et al., The advanced composition explorer. Space Sci. Rev. 86, 1 (1998)

    Article  ADS  Google Scholar 

  • B.T. Tsurutani, E.J. Smith, D.E. Jones, Waves observed upstream of interplanetary shocks. J. Geophys. Res. 88, 5645 (1983)

    Article  ADS  Google Scholar 

  • A.J. Tylka, W.F. Dietrich, A new and comprehensive analysis of proton spectra in ground-level enhanced (GLE) solar particle events, in Int. Cosmic Ray Conf. 31st (2009). http://icrc2009.uni.lodz.pl/proc/pdf/icrc0273.pdf

    Google Scholar 

  • A.J. Tylka, M.A. Lee, A model for spectral and compositional variability at high energies in large, gradual solar particle events. Astrophys. J. 646, 1319 (2006)

    Article  ADS  Google Scholar 

  • A.J. Tylka, D.V. Reames, C.K. Ng, Observations of systematic temporal evolution in elemental composition during gradual solar energetic particle events. Geophys. Res. Lett. 26, 2141 (1999)

    Article  ADS  Google Scholar 

  • A.J. Tylka, P.R. Boberg, R.E. McGuire, C.K. Ng, D.V. Reames, Temporal evolution in the spectra of gradual solar energetic particle events, in Acceleration and Transport of Energetic Particles Observed in the Heliosphere: ACE 2000 Symposium, ed. by R.A. Mewaldt et al., AIP Conference Proceedings, vol. 528 (AIP, New York, 2000), pp. 147–152

    Google Scholar 

  • A.J. Tylka et al., Evidence for remnant flare suprathermals in the source population of solar energetic particles in the 2000 Bastille Day event. Astrophys. J. 558, L59 (2001)

    Article  ADS  Google Scholar 

  • A.J. Tylka et al., Shock geometry, seed populations, and the origin of variable elemental composition at high energies in large gradual solar particle events. Astrophys. J. 625, 474 (2005)

    Article  ADS  Google Scholar 

  • R. Vainio, On the generation of Alfvén waves by solar energetic particles. Astron. Astrophys. 406, 735 (2003)

    Article  ADS  Google Scholar 

  • P. van Nes, R. Reinhard, T.R. Sanderson, K.-P. Wenzel, R.D. Zwickl, The energy spectrum of 35- to 1600-keV protons associated with interplanetary shocks. J. Geophys. Res. 89, 2122 (1984)

    Article  ADS  Google Scholar 

  • L. Wang, R.P. Lin, S. Krucker, G.M. Mason, A statistical study of solar electron events over one solar cycle. Astrophys. J. (2012, submitted)

  • M.E. Wiedenbeck et al., How common is energetic 3He in the inner heliosphere? in Solar Wind 10 Proceedings of the Tenth International Solar Wind Conference, ed. by M. Velli, R. Bruno, F. Malara, AIP Conf. Proc., vol. 679 (AIP, New York, 2003), pp. 652–655

    Google Scholar 

  • G.P. Zank, G. Li, V. Florinski, Q. Hu, D. Lario, C.W. Smith, Particle acceleration at perpendicular shock waves: model and observations. J. Geophys. Res. 111, A06108 (2006). doi:10.1029/2005JA011524

    Article  ADS  Google Scholar 

  • M. Zhang, M.A. Lee, Stochastic acceleration of energetic particles in the heliosphere. Space Sci. Rev. (2011). doi:10.1007/s11214-011-9754-3

    Google Scholar 

Download references

Acknowledgements

The authors wish to acknowledge the hospitality of the International Space Science Institute, the stimulating program of the Workshop on Particle Acceleration in Cosmic Plasmas, and the patience of Dr. Andre Balogh while awaiting this typescript. The contribution of M.A.L. was supported, in part, by NASA grants NNX08AJ13G, NNX11AO97G and NNX12AB32G. The contribution of R.A.M. was sponsored by NASA under grants NNX8AI11G, NNX06AC21G, and under subcontract SA2715-26309 from UC Berkeley under NASA contract NAS5-03131. The contribution of J.G. was supported, in part, by NASA grants NNX11AO64G and NNX10AF24G.

Author information

Authors and Affiliations

  1. Space Science Center, University of New Hampshire, Morse Hall, 8 College Rd., Durham, NH, 03824, USA

    Martin A. Lee

  2. 290-17 Cahill Laboratory, California Institute of Technology, Pasadena, CA, 91125, USA

    R. A. Mewaldt

  3. Department of Planetary Sciences, University of Arizona, 1629 E. University Blvd., Tucson, AZ, 85721, USA

    J. Giacalone

Authors
  1. Martin A. Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. A. Mewaldt
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. J. Giacalone
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Martin A. Lee.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Lee, M.A., Mewaldt, R.A. & Giacalone, J. Shock Acceleration of Ions in the Heliosphere. Space Sci Rev 173, 247–281 (2012). https://doi.org/10.1007/s11214-012-9932-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11214-012-9932-y

Keywords

Search

Navigation