Ghost Images in Helioseismic Holography? Toy Models in a Uniform Medium

Abstract

Helioseismic holography is a powerful technique used to probe the solar interior based on estimations of the 3D wavefield. The Porter–Bojarski holography, which is a well-established method used in acoustics to recover sources and scatterers in 3D, is also an estimation of the wavefield, and hence it has the potential of being applied to helioseismology. Here we present a proof-of-concept study, where we compare helioseismic holography and Porter–Bojarski holography under the assumption that the waves propagate in a homogeneous medium. We consider the problem of locating a point source of wave excitation inside a sphere. Under these assumptions, we find that the two imaging methods have the same capability of locating the source, with the exception that helioseismic holography suffers from “ghost images” (i.e. artificial peaks away from the source location). We conclude that Porter–Bojarski holography may improve the method currently used in helioseismology.

1 Introduction

Local helioseismology is a powerful tool used to probe the 3D interior of the Sun by exploiting the information contained within the acoustic and surface-gravity waves observed at the surface (see, e.g., Gizon and Birch, 2005; Gizon, Birch, and Spruit, 2010). Helioseismic holography is one branch of local helioseismology that aims at imaging the subsurface structure by estimating the wavefield inside the Sun (Lindsey and Braun, 1997, 2000a). One significant achievement of helioseismic holography has been the detection of active regions on the far side of the Sun (far-side imaging: Lindsey and Braun, 2000b). The technique used in far-side imaging, known as phase-sensitive holography, has been validated with synthetic data (see, e.g., Hartlep et al., 2008; Birch et al., 2011; Braun, 2014), and it is extensively used in studying active regions in the near hemisphere (e.g. Braun and Birch, 2008; Braun, 2016).

The fundamental concept of helioseismic holography is that the wavefield can be estimated by the so-called “egression”, which is the back-propagation (in time) of the observed wavefield at the surface into the solar interior (see reviews by Lindsey and Braun, 2000a; Lindsey et al., 2011). The egression can be understood in terms of Huygens’ principle, whereby each point of a wavefront is considered a source, and the wavefield at a later time as a superposition of waves emitted from all of these point sources along the wavefront (see, e.g., Landau and Lifshitz, 1975). Specifically, each arbitrarily small section of the observed wavefield can be regarded as a point source, and the egression as the sum of the back-propagated (in time) waves generated from all these point sources. Therefore, the egression behaves in the same manner as the wavefield propagating backward in time. Furthermore, the propagation of the wavefield forward in time is known as the “ingression”. The ingression can be understood by Huygens’ principle in the same way as the egression, but for the waves that are forward-propagating in time.

Since Huygens’ principle is frequently used in optics and acoustics, it is thus not surprising that techniques similar to the egression/ingression have been used in fields outside helioseismology. In ocean acoustics, Jackson and Dowling (1991) proposed an active method called phase conjugation, which uses the same principle as the egression, to locate acoustic sources. This method records the wavefield on an array of detectors at a fixed surface, and then it creates a time-reversed (or a complex-conjugation in the frequency domain) wave by treating the wavefield observed at each detector as a point source. Jackson and Dowling (1991) argued that the newly created wave will focus on the source of the original wave. This proposed method was later confirmed by experiments in the sea (see, e.g., Kuperman et al., 1998; Song, Kuperman, and Hodgkiss, 1998).

The rigorous mathematical statement of Huygens’ principle is the Helmholtz–Kirchhoff theorem, which states that the wavefield can be reconstructed in 3D space if both the wavefield and its normal derivative are recorded on an arbitrary closed surface (see, e.g., Born and Wolf, 1999). However, the Helmholtz–Kirchhoff theorem is only valid for a source-free medium (Porter and Devaney, 1982). This is not the case for the entirety of the solar interior, where the wavefield is stochastically and ubiquitously excited by near-surface convection. In this case, the medium is not source-free, and to our knowledge, no theory has been established thus far that can reconstruct the wavefield in 3D space directly from observations on a 2D surface.

Although the direct reconstruction of the wavefield is not possible, acoustic sources and scatterers can be estimated in 3D space for a medium that is not source-free. In acoustics, a well-established technique known as Porter–Bojarski (PB) holography can achieve this (see, e.g., Porter and Devaney, 1982; Devaney and Porter, 1985; Devaney, 2012). PB holography is based on an integral that is slightly different from the Helmholtz–Kirchhoff theorem; however, the wavefield and its normal derivative are still required (see Section 2). Instead of reconstructing the wavefield, PB holography produces a 3D image (known as the PB hologram) from a closed surface that is equivalent to the difference between the wavefield and its time-reversal (Porter, 1969). Understanding the PB hologram can be achieved through Huygens’ principle. Specifically, the wavefield and its normal derivative recorded at a surface can be thought of as a dipole and a monopole source, respectively. This means that the PB hologram is also an estimation of the wavefield, and hence it has the potential of being applied to helioseismology in a similar manner to the egression.

With the possible application of PB holography, it is then natural to ask whether this new method better estimates the wavefield than the egression, and hence whether it might improve the current imaging capabilities of helioseismic holography. Previous studies by Skartlien (2001, 2002) have shown that both the egression and the PB hologram are measurements of the local strength of acoustic sources and can be related to the sources via their respective sensitivity kernels. This allows us to refine the scope of the previous question; specifically, which method is more accurate at locating acoustic sources? Comparisons between these methods have been done in ocean acoustics, where Jackson and Dowling (1991) showed that both methods can locate the source. Hence, the authors concluded that the egression is the simplified version of the PB hologram, and chose to use the egression as their preferred method since it is easier to implement. In the case of helioseismology, however, the question of the optimal method has yet to be answered. This is the goal of this article. Additionally, preliminary work by Lindsey and Braun (2004) showed that helioseismic holography suffers from unintended mirror-like images (“ghost images”) that are caused by the use of only a monopole source. An examination of ghost images in the egression and the PB hologram is also a focus of this study.

In this article, we present a proof-of-concept study, where we compare the source-sensitivity kernels of helioseismic holography and PB holography by assuming waves are propagating in a homogeneous medium. Specifically, we examine which method is more accurate at locating acoustic sources, and hence at estimating the wavefield. Additionally, we examine the effect that the observational coverage area has on the kernels. This will provide an opportunity to improve the method currently used in helioseismology. This article is organized as follows: Section 2 states the derivation of source-sensitivity kernels of helioseismic holography (egression) and PB holography, Section 3 states the toy model used in this article, Section 4 compares the two methods with a discussion, and conclusions are provided in Section 5.

2 Source-Sensitivity Kernels

In this section, we present the relation of helioseismic holography and PB holography to acoustic sources. We work entirely in the temporal Fourier domain, using the convention

$$ f(\omega)= \int_{-\infty}^{+\infty} \mathrm{d} t\,F(t) \mathrm{e}^{\mathrm{i}\omega t}, $$

(1)

where $f(\omega)$ is the Fourier transform of a given function $F(t)$.

The egression $[\Phi^{\tiny{\mathrm{LB}}}]$, as described by Lindsey and Braun (1997: LB), is one of the basic quantities used in helioseismic holography,

$$ \Phi^{\tiny{\mathrm{LB}}}_{A}(\boldsymbol{r},\omega)= \int_{A} \mathrm{d}^{2}\boldsymbol{r}'\,G^{*}\bigl(\boldsymbol{r},\boldsymbol{r}', \omega\bigr)\Psi\bigl( \boldsymbol{r}', \omega\bigr), $$

(2)

where $\boldsymbol{r}$ denotes the focal point, $A$ is the coverage of the wavefield $\Psi(\boldsymbol{r}',\omega)$ at any point $\boldsymbol{r}'$ on the solar surface, and $G(\boldsymbol{r},\boldsymbol{r}',\omega)$ is the Green’s function associated with a wave operator defined below, with the asterisk denoting the complex conjugate. For simplicity, we drop the $\omega$ within the function’s arguments for the remainder of this study. Further definitions and explanations concerning the Green’s function are given below.

The PB hologram $\Phi^{\tiny{\mathrm{PB}}}$ is defined by Devaney and Porter (1985),

$$ \Phi^{\tiny{\mathrm{PB}}}_{A}(\boldsymbol{r})= \int_{A} \mathrm{d}^{2}\boldsymbol{r}'\, \bigl\{ \Psi\bigl(\boldsymbol{r}'\bigr)\partial_{n'}\operatorname{Im}G \bigl(\boldsymbol{r},\boldsymbol{r}'\bigr)- \operatorname{Im}G\bigl(\boldsymbol{r}, \boldsymbol{r}'\bigr) \partial_{n'}\Psi\bigl(\boldsymbol{r}' \bigr) \bigr\} , $$

(3)

where $\partial_{n'}$ denotes the outward-normal derivative with respect to $\boldsymbol{r}'$, and $\operatorname{Im}G$ is the imaginary part of the Green’s function.

In order to relate $\Phi^{\tiny{\mathrm{LB}}}$ and $\Phi^{\tiny{\mathrm{PB}}}$ to the acoustic sources, we first need to determine the impulse response function [$G$, the Green’s function] of the wave equation. Here we assume that the wavefield $[\Psi]$ is related to the sources through the application of a linear wave operator $[\mathcal{L}]$,

$$ \mathcal{L}\Psi(\boldsymbol{r})=S(\boldsymbol{r}), $$

(4)

where $S(\boldsymbol{r})$ is the source function. For generality, we choose not to explicitly state ℒ here. The Green’s function is the impulse response of Equation 4, and it is defined as the solution to

$$ \mathcal{L}G(\boldsymbol{r},\boldsymbol{r}_{\mathrm{s}})=\delta(\boldsymbol{r}-\boldsymbol{r}_{\mathrm{s}}), $$

(5)

where $\delta(\boldsymbol{r}-\boldsymbol{r}_{\mathrm{s}})$ is the Dirac delta function and $\boldsymbol{r}_{\mathrm{s}}$ is the location of the source. One property of the Green’s function, which is crucial to deriving source-sensitivity kernels, is that it can be used to solve Equation 4 through

$$ \Psi\bigl(\boldsymbol{r'}\bigr)= \int_{\mathbb{R}^{3}} \mathrm{d}^{3}\boldsymbol{r}_{\mathrm{s}}\, G \bigl(\boldsymbol{r}',\boldsymbol{r}_{\mathrm{s}}\bigr)S(\boldsymbol{r}_{\mathrm{s}}). $$

(6)

Through expansion of $\Psi$ in Equation 2 with the definition in Equation 6, the egression becomes

$$ \Phi^{\tiny{\mathrm{LB}}}_{A}(\boldsymbol{r})= \int_{A} \mathrm{d}^{2}\boldsymbol{r}' \,G^{*}\bigl(\boldsymbol{r},\boldsymbol{r}'\bigr) \int_{\mathbb{R}^{3}} \mathrm{d}^{3}\boldsymbol{r}_{\mathrm{s}}\, G \bigl( \boldsymbol{r}',\boldsymbol{r}_{\mathrm{s}}\bigr)S(\boldsymbol{r}_{\mathrm{s}}), $$

(7)

and through a change in the order of integration, one obtains the definition for the source sensitivity kernel $[K^{\tiny{\mathrm{LB}}}]$ for the egression

$$ \Phi^{\tiny{\mathrm{LB}}}_{A}(\boldsymbol{r})=\frac{1}{4\pi} \int_{\mathbb{R}^{3}} \mathrm{d}^{3}\boldsymbol{r}_{\mathrm{s}}\, K^{\tiny{\mathrm{LB}}} _{A}(\boldsymbol{r},\boldsymbol{r}_{\mathrm{s}}) S( \boldsymbol{r}_{\mathrm{s}}), $$

(8)

where

$$ K^{\tiny{\mathrm{LB}}}_{A}(\boldsymbol{r},\boldsymbol{r}_{\mathrm{s}})=4\pi \int_{A} \mathrm{d}^{2}\boldsymbol{r}' \,G^{*}\bigl(\boldsymbol{r},\boldsymbol{r}'\bigr) G\bigl( \boldsymbol{r}',\boldsymbol{r}_{\mathrm{s}}\bigr). $$

(9)

We note that the $4\pi$ factor is included here such that $K^{\tiny {\mathrm{LB}}}$ possesses a desired near-unitary amplitude for this study.

The same procedure is repeated for the derivation of the PB hologram by expanding $\Psi$ in Equation 3 with Equation 6 and changing the order of integration:

$$\begin{aligned} \Phi^{\tiny{\mathrm{PB}}}_{A}(\boldsymbol{r}) =&\frac{1}{4\pi} \int_{\mathbb{R}^{3}} \mathrm{d}^{3}\boldsymbol{r}_{\mathrm{s}}\, K^{\tiny{\mathrm{PB}}} _{A}(\boldsymbol{r},\boldsymbol{r}_{\mathrm{s}})S( \boldsymbol{r}_{\mathrm{s}}), \end{aligned}$$

(10)

$$\begin{aligned} K^{\tiny{\mathrm{PB}}}_{A}(\boldsymbol{r},\boldsymbol{r}_{\mathrm{s}}) =&4\pi \int_{A} \mathrm{d}^{2}\boldsymbol{r}'\, \bigl\{ G\bigl(\boldsymbol{r}',\boldsymbol{r}_{\mathrm{s}}\bigr)\partial_{n'} \operatorname{Im}G\bigl(\boldsymbol{r},\boldsymbol{r}'\bigr) -\operatorname{Im}G \bigl(\boldsymbol{r},\boldsymbol{r}'\bigr) \partial _{n'} G\bigl( \boldsymbol{r}',\boldsymbol{r}_{\mathrm{s}}\bigr) \bigr\} , \end{aligned}$$

(11)

where $K^{\tiny{\mathrm{PB}}}_{A}$ is the source-sensitivity kernel of the PB hologram.

A comparison of the egression and the PB hologram requires only the knowledge of their respective source-sensitivity kernels, whereas details of the source function are not needed. Therefore, we examine the source-sensitivity kernels of the two imaging methods in this study. We compare the two source kernels under simplifying assumptions about the medium in which the waves propagate. We note that in practice, the egression power $|\Phi^{\tiny{\mathrm{LB}}}|^{2}$ is used to estimate the location of acoustic sources, since the wavefield in the Sun is stochastically excited (see, e.g., Lindsey and Braun, 1997; Hanson, Donea, and Leka, 2015). Therefore, we also compare the squared modulus of the source kernels.

3 Toy Model: Waves in a Homogeneous Medium

With Equations 9 and 11 in hand, we require the computation of the Green’s functions in order to determine the source-sensitivity kernels. In general, a Green’s function can be obtained numerically for any given linear operator $[\mathcal{L}]$. However, as stated in the introduction, we examine a homogeneous medium, and therefore the Green’s function can be computed analytically.

We consider this homogeneous medium in $\mathbb{R}^{3}$ space with a constant sound speed $c=10^{5}~\mbox{m}\,\mbox{s}^{-1}$, and we adopt the linear wave operator,

$$ \mathcal{L}=k^{2}+\nabla^{2},\quad k= \frac{\omega+\textrm{i}\gamma}{c} , $$

(12)

where $k$ is the wavenumber, $\omega$ is the angular frequency and $\gamma$ is the damping rate. The solution of Equation 5 with the above wave operator and free boundary condition is given by

$$ G\bigl(\boldsymbol{r},\boldsymbol{r}'\bigr)=-\frac{1}{4\pi}\frac{\exp ( \mathrm{i}k| \boldsymbol{r}-\boldsymbol{r}'| ) }{|\boldsymbol{r}-\boldsymbol{r}'|}, $$

(13)

which is also known as the outgoing free-space Green’s function (Born and Wolf, 1999). In this study, we set the damping rate $[\gamma]$ to be $0.1\%$ of the angular frequency, and we use a Cartesian coordinate system $(x,y,z)$ with its origin at the center of a sphere $\textrm{V}_{\odot}$ with the radius $\textrm{R}_{\odot}=696~\mbox{Mm}$.

Current observational capabilities mean that we can only observe the wavefield on a fraction of the solar surface. To study the consequence of this limitation on observations, we examine both the case where the entire surface is observed and the case where only a fraction of the solar surface is observed. In these cases, we assume that the sources are located along the $z$-axis and that the coverage is symmetric with respect to the $z$-axis and is centered above the North Pole $(0,0,\textrm{R}_{\odot})$. Under these assumptions, $K^{\tiny{\mathrm{LB}}}$ and $K^{\tiny{\mathrm{PB}}}$ are axisymmetric about the $z$-axis.

4 Results

4.1 Source-Sensitivity Kernels at 3 mHz

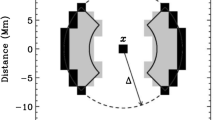
Here we examine the source-sensitivity kernels [$K^{\tiny{\mathrm{LB}}}$ and $K^{\tiny{\mathrm{PB}}}$] at a frequency of $\omega/2\pi=3$ mHz. Figure 1 shows 2D slices of both the real and imaginary parts of $K^{\tiny{\mathrm{LB}}}$ and $cK^{\tiny{\mathrm{PB}}}/\omega$ through the $z$-axis, for the source locations at $z_{\mathrm{s}}=0.9\textrm{R}_{\odot}$ (panels a to h) and $-0.9\textrm{R}_{\odot}$ (panels i to l) on the $z$-axis. The factor $c/\omega$ is added to $K^{\tiny{\mathrm{PB}}}$ so that the kernel is dimensionless like the egression. The first row of panels shows the source-sensitivity kernels under the assumption that the entire surface is observed. The remaining rows show the kernels assuming a coverage of 60 degrees from the North Pole. Considering all panels, both $\operatorname{Re}[K^{\tiny{\mathrm{LB}}}]$ and $\operatorname{Re}[K^{\tiny {\mathrm{PB}}}]$ peak at the source, while in comparison, $\operatorname{Im}[K^{\tiny{\mathrm{LB}}}]$ and $\operatorname{Im}[K^{\tiny{\mathrm{PB}}}]$ are negligible if the source is located at the near side. These results demonstrate that $\operatorname{Re}[K ^{\tiny{\mathrm{LB}}}]$ and $\operatorname{Re}[K^{\tiny{\mathrm{PB}}}]$ can both locate the source in either of these coverage geometries. In the case of sources located on the far side, all of the kernels have become less localized. While these kernels can locate the sources, we also see that the egression kernels (both the real and imaginary parts) have “ghost images” above the surface, while the PB holograms do not. These ghost images appear as peaks at points away from the source location. We note that we here also observed ghost images below the surface in the egression, when the source is above the surface. This suggests that the egression cannot distinguish sources from below and above the surface, since one cannot differentiate sources and ghosts. The PB holograms do not suffer from this problem. Further explanations and discussions concerning the ghost images are given in Section 5.1.

Figure 1

2D slices of the real and imaginary parts of $K^{\tiny {\mathrm{LB}}}$ and $K^{\tiny{\mathrm{PB}}}$ through the $z$-axis, when the entire surface (top row) and 60 degrees around the North Pole (middle and bottom rows) can be observed. The location of the source is at the focal point of the crosshairs (solid-black lines) in each plot, where $z_{\mathrm{s}}=0.9\textrm{R}_{\odot}$ in the top and middle rows and $z_{\mathrm{s}}=-0.9\textrm{R}_{\odot}$ in the bottom row. A simple geometry plot is given on the left of each row, with the source location (asterisk), the solar center (large dot), the solar surface (dashed lines), and the coverage area (solid arc) overplotted.

For a more focused comparison of the kernels in Figure 1, Figure 2 shows 1D slices of $K^{\tiny{\mathrm{LB}}}$ and $K^{\tiny{\mathrm{PB}}}$ along the $z$-axis with the real parts shown in panels a, c, and e, and the imaginary parts in panels b, d, and f. $\operatorname{Re}[K^{\tiny{\mathrm{LB}}}]$ and $\operatorname{Re}[K^{\tiny {\mathrm{PB}}}]$ again have peaks at the source location. Here we see that despite the coverage geometry, $\operatorname{Im}[K^{\tiny{\mathrm{LB}}}]$ and $\operatorname{Im}[K^{\tiny {\mathrm{PB}}}]$ are always zero at the source location, with the peaks seen in Figure 1 surrounding the source location. This suggests that $\operatorname{Im}[K^{\tiny{\mathrm{LB}}}]$ and $\operatorname{Im}[K^{\tiny{\mathrm{PB}}}]$ cannot pinpoint the exact source location. In the case of sources located on the far side, $K^{\tiny {\mathrm{LB}}}$ and $K^{\tiny{\mathrm{PB}}}$ are both highly oscillatory and non-localized, and hence recovering the source location may be problematic with observations at a single frequency.

Figure 2

1D slices of $K^{\tiny{\mathrm{LB}}}$ (blue solid) and $K^{\tiny{\mathrm{PB}}}$ (red dashed) shown in Figure 1 along the $z\mbox{-axis}$. The real parts are plotted in panels a, c, and e, and the imaginary parts in panels b, d, and f. The geometry is shown on the left with the addition of the slice length (blue line).

Figure 3 shows 1D slices of $K^{\tiny {\mathrm{LB}}}$ and $K^{\tiny{\mathrm{PB}}}$ along a line that is perpendicular to the $z$-axis and passes through the source. Owing to axial symmetry, only half of the slice is plotted. Here the imaginary parts of $K^{\tiny{\mathrm{LB}}}$ and $K^{\tiny{\mathrm{PB}}}$ are not shown since they are negligible compared to the real parts. Unlike the vertical slices, neither $K^{\tiny{\mathrm{LB}}}$ nor $K^{\tiny {\mathrm{PB}}}$ have ghost images, and they are less oscillatory when the source is located at the far side.

Figure 3

1D slices of $K^{\tiny{\mathrm{LB}}}$ (blue solid) and $K^{\tiny{\mathrm{PB}}}$ (red dashed) in Figure 1 along the line perpendicular to the $z$-axis. The imaginary parts are negligible compared to the real parts, and they are not shown in the figure. Because of the axial symmetry, only half of the slice is shown. The geometry of the slices is shown on the left, with the slice length shown in blue.

4.2 Kernels Averaged over Frequency

Specifically, the two methods are highly oscillatory and non-localized for the source located at the far side for observations made at a single frequency, and the egression suffers from ghost images for the source located at the near side. One possible solution to these problems is to average kernels over a number of frequencies, since the ghost images for the source located at the near side and the side-lobes for the source located at the far side may peak at different locations for different frequencies.

Figure 4 shows 1D vertical slices of $K^{\tiny{\mathrm{LB}}}$ and $K^{\tiny{\mathrm{PB}}}$ averaged from 41 frequencies equally distributed from 1 to 5 mHz. A Gaussian weight function centered at 3 mHz and with a standard deviation of 1 mHz was applied for the averaging. From these results, it is clear that averaging the kernels over frequency reduces the amplitude of the ghost images for the near-side source and the side-lobes for the far-side source. The averaged kernels along the horizontal direction are similar to the kernels with a single frequency, and as such they are not shown here.

Figure 4

1D slices of kernels averaged over frequencies using a Gaussian weight function centered at 3 mHz with a standard deviation of 1 mHz. Here we use a bar to denote the averaged quantity. The observational coverage $A$ is depicted in the left panels (thick arcs). The frequency averaging reduces the amplitudes of the ghost images for the near-side source and the side-lobes for the source on the far side.

As mentioned in Section 2, the egression power, which is related to the source covariance via $|K^{\tiny{\mathrm{LB}}}|^{2}$, has been used in observations as estimates of the acoustic sources. Therefore, the effect of averaging $|K^{\tiny{\mathrm{LB}}}|^{2}$ and $|K^{\tiny{\mathrm{PB}}}|^{2}$ over different frequencies is also of great interest. Figure 5 shows a comparison of $|K^{\tiny{\mathrm{LB}}}|^{2}$ and $|K^{\tiny {\mathrm{PB}}}|^{2}$ with or without averaging over different frequencies. Only the slices along the vertical direction are shown, as the difference between $|K^{\tiny{\mathrm{LB}}}|^{2}$ ($|K^{\tiny {\mathrm{PB}}}|^{2}$) from a single frequency at 3 mHz and averaged from 1 to 5 mHz along the horizontal direction is small. In the vertical direction, averaging $|K^{\tiny{\mathrm{LB}}}|^{2}$ and $|K^{\tiny {\mathrm{PB}}}|^{2}$ over different frequencies reduces the amplitude of the ghosts when the source is located at the near side, and improves the spatial resolution when the source is located at the far side.

Figure 5

1D slices of $|K^{\tiny{\mathrm{LB}}}|^{2}$ and $|K^{\tiny{\mathrm{PB}}}|^{2}$ in a plane containing the $z$-axis. The left panels show a single frequency of 3 mHz. The right panels show averages over frequencies using a Gaussian weight function centered at 3 mHz with a standard deviation of 1 mHz. Averaging the kernels over frequencies reduces the amplitude of the ghosts when the source is located on the near side, and it improves the spatial resolution when the source is located on the far side.

4.3 Dependence of the Spatial Resolution on the Coverage

The results thus far have shown that both of the methods can locate the source, although the egression has the complication of ghost peaks. The question then arises of how well these methods resolve the sources with differing observational coverages. We define the spatial resolution the egression and the PB hologram as the full-width at half-maximum (FWHM) of $|K^{\tiny{\mathrm{LB}}}|^{2}$ and $|K^{\tiny{\mathrm{PB}}}|^{2}$, respectively. Figures 2 and 3 show that both of the methods behave differently in the vertical and horizontal directions, and the FWHMs in these two directions are therefore considered separately. Additionally, to quantify the effect of averaging kernels over different frequencies, we considered the FWHM for kernels from a single frequency at 3 mHz and the value averaged over frequencies from 1 to 5 mHz.

Figure 6 shows the FWHM of $|K^{\tiny{\mathrm{LB}}}|^{2}$ and $|K^{\tiny{\mathrm{PB}}}|^{2}$ as a function of the angle $[\theta_{h}]$, which defines the observational coverage (cap of area $A$). The FWHMs along the vertical (top row) and horizontal (bottom row) directions are considered in the case of kernels at 3 mHz (left column) and averaged from 1 to 5 mHz (averaged kernel, right column). At 3 mHz, the difference between the two imaging methods is small, which implies that either method has the same capability of resolving the source. Furthermore, the FWHM is close to the resolution limit despite the size of the coverage area when the source is located at the near side ($z_{\mathrm{s}}=0.9\textrm{R}_{\odot}$). When the source is located at the far-side ($z_{\mathrm{s}}=-0.9\textrm{R}_{\odot}$), the resolution improves (FWHM decreases) with increasing coverage. When averaging over different frequencies, a clear improvement of the spatial resolution can be found along the vertical direction when the source is located on the far side, while the spatial resolution is almost the same as before for the other cases.

Figure 6

FWHM of $|K^{\tiny{\mathrm{LB}}}|^{2}$ and $|K^{\tiny {\mathrm{PB}}}|^{2}$ as a function of the angle $[\theta_{h}]$, which defines the observational coverage (cap of area $A$). The FWHM along two directions, horizontal and vertical, is shown in the case of a near-side source ($z_{\mathrm{s}}=0.9\textrm{R}_{\odot}$, blue) and a far-side source ($z _{\mathrm{s}}=-0.9\textrm{R}_{\odot}$, red). The theoretical resolution limit of $\lambda/2$ is also shown with a horizontal black line. Additionally, the results for the kernels at a single frequency $\omega/2\pi= 3$ mHz and the frequency-averaged kernels are shown in the left and right columns, respectively.

5 Discussion

5.1 Ghost Images in the Egression

The appearance of ghost images in the egression can be understood by Huygens’ principle, whereby each arbitrarily small section of the observed wavefield is regarded as a point source, and the egression as a superposition of the back-propagated (in time) waves generated from all of the point sources. Furthermore, each newly created wave is spherically symmetric with respect to its source location in a homogeneous medium, and thus it will propagate in all directions with the same behavior. This is the cause of the ghost images. A clear example of this is evident when the wavefield is recorded on a plane, where all of the newly created waves are symmetric with respect to the recording surface, and hence the egression will focus on both the source location and its counterpart on the other side of the surface (see Figure 7 for an example). When the wavefield is observed on a sphere, however, the newly created waves are no longer symmetric with respect to the surface, and the ghost images show a complicated diffraction pattern that is due to the interference among the newly created waves (Figure 1). This provides a simple explanation for the ghost images seen in the egression above the surface (see also Lindsey and Braun, 2004).

Figure 7

2D slice of the real (left panel) and imaginary (right panel) part of $K^{\tiny{\mathrm{LB}}}$ through the $z$-axis when the wavefield is observed at the $z=0$ plane. Here the coverage is a circle that is centered at the origin and has a radius $\textrm{R}_{\odot}$. The source is located along the $z$-axis at $z_{\mathrm{s}} = -0.1\textrm{R} _{\odot}$ and is indicated by the focus of the crosshairs in each plot.

The PB hologram does not suffer from ghost images like the egression, since it includes not only a monopole source, but also a dipole source, which is not symmetric with respect to the source location. Additionally, the amplitudes of the monopole and dipole sources are chosen such that the PB hologram only focuses on the source location.

Future work should include a solar-like density stratification to confirm this simple explanation. The sharp drop in density at the solar surface leads to a reflection of the waves below 5.3 mHz, which is not captured in our toy model.

We also note that Lindsey and Braun (2005a,b) proposed that ghost images may explain the presence of phase anomalies observed around active regions in phase-sensitive holography. For further implications and discussions of the ghost images in helioseismic holography, we refer to Lindsey and Braun (2004).

5.2 Ingression and the PB Hologram

We did not consider the ingression in our analysis. The ingression is an equally important quantity used in helioseismic holography, which is an estimation of the location at which the wavefield converges by propagating the wavefield forward in time (Lindsey and Braun, 1997). So far, we have considered the wavefield $\Psi$ as diverging away from the source. However, to compare the ingression and the PB hologram, a wavefield that converges from infinity to the source location is desired. Such a wavefield can be achieved by considering the wavefield diverging from the source as before, but with the reversed sign in time, i.e. $\Psi(\boldsymbol{r},-t)$. In the frequency domain, this time-reversal corresponds to taking the complex conjugate. Additionally, the wave number [$k$] in the wave equation is also conjugated and thus the wavefield decays when propagating toward the source location (Devaney, 2012). In this case, the ingression is

$$ \Phi^{\tiny{\mathrm{LB}}}_{A,-}(\boldsymbol{r},\omega)= \int_{A} \mathrm{d} ^{2}\boldsymbol{r}'\,G\bigl( \boldsymbol{r},\boldsymbol{r}',\omega\bigr)\Psi^{*}\bigl( \boldsymbol{r}',\omega\bigr), $$

(14)

and the PB hologram becomes

$$ \Phi^{\tiny{\mathrm{PB}}}_{A,-}(\boldsymbol{r},\omega)= \int_{A} \mathrm{d} ^{2}\boldsymbol{r}' \bigl\{ \Psi^{*}\bigl(\boldsymbol{r}',\omega\bigr) \partial_{n'} \operatorname{Im}G\bigl( \boldsymbol{r},\boldsymbol{r}',\omega\bigr)- \operatorname{Im}G\bigl(\boldsymbol{r},\boldsymbol{r}',\omega\bigr) \partial _{n'}\Psi^{*}\bigl(\boldsymbol{r}',\omega\bigr)\bigr\} . $$

(15)

We can see that $\Phi^{\tiny{\mathrm{LB}}}_{-}$ and $\Phi^{\tiny{\mathrm{PB}}}_{-}$ are simply the complex conjugates of $\Phi^{\tiny{\mathrm{LB}}}$ and $\Phi^{\tiny{\mathrm{PB}}}$. Since we have discussed the real and imaginary parts and the power of $\Phi^{\tiny{\mathrm{PB}}}$ and $\Phi^{\tiny{\mathrm{LB}}}$ separately in the results, those of $\Phi^{\tiny{\mathrm{LB}}}$ ($\Phi^{\tiny{\mathrm{PB}}}$) will be the same as $\Phi^{\tiny{\mathrm{LB}}}_{-}$ ($\Phi^{\tiny{\mathrm{PB}}}_{-}$). In particular, $\Phi^{\tiny{\mathrm{LB}}}_{-}$ will also have ghost images while $\Phi^{\tiny{\mathrm{PB}}}_{-}$ will not, and $| \Phi^{\tiny{\mathrm{LB}}}_{-}|^{2}$ and $|\Phi^{\tiny{\mathrm{PB}}} _{-}|^{2}$ will have the same spatial resolution when imaging acoustic sources.

5.3 Application to Stereoscopic Helioseismology

The results in Section 4.3 showed that the spatial resolution of the hologram on the far side increases as the coverage area increases. Thus the resolution has a fundamental limit when observing from a single vantage point. It has been suggested to combine observations from two or several vantage points to increase the observation coverage and therefore to improve the spatial resolution (and signal-to-noise ratio) of holography. Stereoscopic helioseismology is believed to be our best chance to probe the subsurface structure in the polar regions and the deep convection zone, which is crucial for understanding the 11-year solar cycle (see, e.g., Ruzmaikin and Lindsey, 2003). This conjecture, however, has not been studied in detail.

Figure 8 shows the PB hologram on the solar surface with a Dirac delta source located 0.7 Mm below the surface at $270^{\circ}$ longitude along the Equator. Different coverage geometries are considered in the case of a single spacecraft (top row), two spacecraft in the Ecliptic (middle row), and two spacecraft with one in the Ecliptic and the other at $45^{\circ}$ inclination (bottom row). Here only the real parts of the PB hologram are shown, since the imaginary parts are negligible. The results show a clear improvement of the spatial resolution when a second spacecraft is added, whereas the FWHM along the Equator is about twice smaller than that of a single spacecraft. Additionally, the spatial resolution is increased along the great circle (black-dashed line) at the intersection of the plane that contains the center of the sphere and the two spacecraft.

Figure 8

2D slices of $\operatorname{Re}[K^{\tiny{\mathrm{PB}}}]$ at the solar surface for observations from a single spacecraft (top row), two spacecraft in the Ecliptic (middle row), and two spacecraft with one in the Ecliptic and the other at $45^{\circ}$ inclination (bottom row). Here the source is located 0.7 Mm below the surface at $270^{\circ}$ longitude along the Equator, and the plots are shown after divided by the maximum value of $\operatorname{Re}[K^{\tiny{\mathrm{PB}}}]$. We note that $\operatorname{Im}[K^{\tiny{\mathrm{PB}}}]$ is negligible, and as such is not shown here. We plot $\operatorname{Re}[K^{\tiny{\mathrm{PB}}}]$ on the entire surface in the left column, where the boundary of the coverage is marked by a red curve and the point below the spacecraft by a cross. Additionally, a zoom of images around the source location is shown in the right column, where a circle centered above the source location with a diameter of the wavelength is added in each plot. The spatial resolution is clearly improved when a second spacecraft is added. Furthermore, a preferred direction that possesses higher spatial resolution is found along the great circle (black-dashed line) that intersects the points below the two spacecraft.

Stereoscopic helioseismology might be implemented in future space missions such as Solar Orbiter and Solar Activity Far Side Investigation (see, e.g., Sekii et al., 2015 and references therein) together with observations collected from the ground (Global Oscillation Network Group) or from near-Earth orbit (Solar Dynamics Observatory). In particular, the Polarimetric and Helioseismic Imager onboard Solar Orbiter is to be launched soon and will provide high-resolution line-of-sight velocity and continuum intensity at the photosphere, which are suitable for helioseismic studies (Woch and Gizon, 2007; Müller et al., 2013; Löptien et al., 2015). The orbit of Solar Orbiter will have a period of 168 days during the nominal mission and reach a heliographic latitude of up to $25^{\circ}$ ($35^{\circ}$ during an extended mission) (Müller et al., 2013). This means that Solar Orbiter will cover a wide range of spacecraft–Sun–Earth angles to test stereoscopic helioseismology.

6 Outlook

We found that helioseismic holography and PB holography are similar techniques, with the exception that the egression and the ingression suffer from ghost images. In principle, we could apply the PB holograms to phase-sensitive holography by replacing the egression and the ingression with the appropriate $\Phi^{\tiny{\mathrm{PB}}}$ and $\Phi^{\tiny{\mathrm{PB}}}_{-}$. Our toy model suggests that the PB holograms will improve current helioseismic holography since they do not suffer from ghost images. However, additional modeling work is needed. Future studies should consider random acoustic sources and scatterers. Furthermore, the computations must be carried out in a solar-like stratified background medium. Finally, in order to implement PB holography, a method for determining the normal derivative of the wavefield needs to be developed.