Propagation of Long-Wavelength Nonlinear Slow Sausage Waves in Stratified Magnetic Flux Tubes

Abstract

The propagation of nonlinear, long-wavelength, slow sausage waves in an expanding magnetic flux tube, embedded in a non-magnetic stratified environment, is discussed. The governing equation for surface waves, which is akin to the Leibovich–Roberts equation, is derived using the method of multiple scales. The solitary wave solution of the equation is obtained numerically. The results obtained are illustrative of a solitary wave whose properties are highly dependent on the degree of stratification.

1 Introduction

The emergence of magnetic flux in the Sun is inhomogeneous, with isolated magnetic flux tubes being a common form of structuring. These tubes form an “elastic medium” and may therefore act as waveguides. The propagation of linear waves along magnetic cylinders has been studied extensively (see, for example, Defouw, 1976 or Roberts, 1981, or the reviews by Andries et al., 2009, De Moortel, 2009, Mathioudakis, Jess, and Erdélyi, 2013 or Wang, 2011). Aspects of the propagation of nonlinear waves have also been studied, with the relevant theory and a number of important results summarised in Ruderman (2003), Ruderman (2006) and Ballai and Ruderman (2011).

The propagation of nonlinear MHD waves (solitons) was first studied in the context of solar physics by Roberts and Mangeney (1982). The propagation of nonlinear wave modes in slabs was discussed more extensively in a series of papers. Merzljakov and Ruderman (1985) derived the Benjamin–Ono equation governing wave propagation in a vertical magnetic slab embedded in a field-free atmosphere. They also estimated the energy transfer of a propagating soliton in a vertically homogeneous atmosphere, and showed that a soliton solution may exist in a stratified magnetic slab. Next, Molotovshchikov and Ruderman (1987) derived an equation governing the propagation of nonlinear slow sausage waves along a magnetic flux tube, again, in a vertically homogeneous atmosphere, but with the added feature of a non-zero external magnetic field $(B_{e} \ne 0)$. Independently, Roberts (1985) obtained the governing equations in both geometries, in the case where the external magnetic field is zero $(B_{e} = 0)$. The findings of Molotovshchikov and Ruderman (1987) were similar to those of Roberts (1985), with the exception that, while their equation possessed a more complicated form of the dispersive term, it was open to numerical analysis. These results, together with those of Molotovshchikov (1989), confirmed the existence of solitary MHD wave solutions to the governing equation whose properties on collision are similar to those of solitons.

Several recent developments of the aforementioned models may be found. A discussion of the use of the thin flux tube approximation, its limitations, and the two-mode approximation may be found in Zhugzhda (2002). Zhugzhda (2004) studied the solutions of slow nonlinear MHD equations in the form of shock waves, while Zhugzhda (2005) derived a new set of equations without making use of the long-wavelength approximation. Numerically, Sakai et al. (2000) studied the impact that gravitational stratification has on the upward and downward propagation of nonlinear MHD waves in flux tubes, while Erdélyi and Fedun (2006) performed simulations modelling excitation, time-dependent propagation, and interaction of solitary waves in solar atmospheric plasmas. More recently, Chargeishvili and Japaridze (2016) found that the propagation of a modulated MHD soliton may cause the temperature of a plasma to rise in the peripheral regions of a magnetic flux tube.

From an observational point of view, Zaqarashvili, Kukhianidze, and Khodachenko (2010) suggested that a series of observations by the Solar Optical Telescope on board the Hinode satellite confirms the existence of slow sausage solitons, propagating in a stratified atmosphere. However, their theoretical analysis of the observations made use of a model of a soliton in a magnetic slab, where a tube would have been better suited.

The present work deals with extending the research of Molotovshchikov and Ruderman (1987) so that it includes the effects of gravitational stratification and radius expansion of the flux tube. We begin by establishing how the undisturbed magnetic field, pressures and densities are related to the varying radius of the tube, and to each other. Next, we employ the thin flux tube approximation and make use of the method of multiple scales to expand the ideal MHD equations. We then reduce these equations to a single nonlinear integro-differential equation. The equation obtained by Molotovshchikov and Ruderman (1987) is then shown to be a simplified case of that obtained here. Lastly, we reduce the governing equation to a form more suitable to analysis, and we numerically obtain a series of solitary wave solutions. The properties of these solutions, including speed–amplitude relations, dependence on stratification, and width–amplitude relations, are then discussed.

2 The Basic State

We consider the undisturbed state to be a vertically straight magnetic flux tube, with vertically variable cross-section, embedded in a stratified field-free atmosphere. The motion is assumed to be axisymmetric, such that in the cylindrical coordinate system $(r, \theta, z)$, the dependent variables are independent of $\theta$, and the azimuthal components of velocity and of the magnetic field are null. We also assume that the boundary of the flux tube is defined by $r = r_{0}(z)$. Figure 1 illustrates a vertical section of a soliton propagating on the boundary of the tube, and a sausage wave.

Figure 1

A soliton, and a sausage wave, respectively, represented at the boundary of the flux tube.

We suppose that the exterior pressure $p_{e0}$ and the exterior density $\rho_{e0}$ depend on $z$ only, and are related by the equation

$$ \frac{\mathrm{d}p_{e0}}{\mathrm{d} z} = - g \rho_{e0}, $$

(1)

where $g$ is the gravitational acceleration.

Inside the tube, the equilibrium quantities, namely the kinetic pressure $p_{0}$, the density $\rho_{0}$, and the magnetic induction $\boldsymbol {B}_{0}$ depend on $r$ and $z$ only. We suppose that the azimuthal component of the magnetic field is zero, such that $\boldsymbol {B}_{0} = (B_{r0}, 0, B_{z0})$, and also that $\nabla \times \boldsymbol {B}_{0} = 0$. Finally, it is assumed that the atmospheric density scale height $H$ is much greater that the radius of the tube $(r_{0} \ll H)$, such that the effect of gravity is weak, but not negligible.

We introduce the magnetic vector potential $\boldsymbol {A} = (0, A, 0)$. The magnetic field, density, and kinetic pressure inside the tube can therefore be defined by the following set of equations and boundary conditions:

$$\begin{aligned} & B_{0r} = - \frac{\partial A}{\partial z}, \qquad B_{0z} = \frac{1}{r} \frac{\partial (rA)}{\partial r}, \qquad \nabla^{2} \boldsymbol {A} = 0, \end{aligned}$$

(2)

$$\begin{aligned} & \frac{\partial p_{0}}{\partial z} = - g \rho_{0}, \qquad \frac{\partial p_{0}}{\partial r} = 0, \end{aligned}$$

(3)

$$\begin{aligned} & \frac{1}{2 \mu_{0}} \biggl[ \biggl( \frac{\partial A}{\partial z} \biggr)^{2} + \biggl( \frac{1}{r} \frac{\partial (rA)}{\partial r} \biggr)^{2} \biggr] + p_{0} = p_{e0} \quad \text{at} \ r = r_{0}(z), \end{aligned}$$

(4)

$$\begin{aligned} & rA = \text{constant} \quad \text{at} \ r = r_{0}(z), \end{aligned}$$

(5)

$$\begin{aligned} & \frac{\partial \rho_{0}}{\partial r} = 0, \qquad \frac{\partial A}{\partial z} = 0 \quad \text{at} \ r=0. \end{aligned}$$

(6)

Equation (2) is derived using only the definition of the vector potential $\boldsymbol {A}$, Equation (4) denotes the balance of pressure, Equation (5) is related to flux conservation, and Equation (6) is the condition of the symmetry of the tube with respect to the $z$-axis.

Let $r_{0}/H \sim \mu \ll 1$. Introducing $\zeta = \mu z$ we rewrite the set of equations and boundary conditions for $A$ as

$$\begin{aligned} & \mu^{2} \frac{\partial^{2} A}{\partial \zeta^{2}} + \frac{\partial}{\partial r} \biggl( \frac{1}{r} \frac{\partial (rA)}{\partial r} \biggr) = 0, \end{aligned}$$

(7)

$$\begin{aligned} & \frac{1}{2 \mu_{0}} \biggl[ \mu^{2} \biggl( \frac{\partial A}{\partial z} \biggr)^{2} + \biggl( \frac{1}{r} \frac{\partial (rA)}{\partial r} \biggr)^{2} \biggr] = p_{e0} - p_{0}, \quad \text{at} \ r = r_{0}(\zeta), \end{aligned}$$

(8)

$$\begin{aligned} & A = \text{constant} \quad \text{at} \ r = 0, \end{aligned}$$

(9)

$$\begin{aligned} & rA = \text{constant} \quad \text{at} \ r = r_{0}( \zeta). \end{aligned}$$

(10)

Using Equations (7), (8), and (9) we obtain

$$ A = \pm \frac{1}{2} r \bigl[ 2 \mu_{0} (p_{e} - p_{0}) \bigr]^{1/2} + O\bigl( \mu^{2}\bigr). $$

(11)

Now, taking Equations (10) and (11) we obtain

$$ \pm \bigl[2 \mu_{0} (p_{e} - p_{0}) \bigr]^{1/2} = S r_{0}^{-1}(\zeta) + O\bigl( \mu^{2}\bigr). $$

(12)

In Equation (12), $S$ is an arbitrary constant, making the choice of sign on the left-hand side arbitrary. We choose the left-hand side to be positive and proceed with the derivation.

By using Equations (1)–(3), (11), and (12) we derive the following set of relations defining the undisturbed state, accurate to order $\mu$:

$$\begin{aligned} \begin{aligned} & \rho_{0} = - \frac{\mu}{g} \frac{\text{d}p_{0}}{\text{d}\zeta}, \qquad p_{e0} = p_{0} + \frac{S^{2}}{2\mu_{0} r_{0}^{4}}, \qquad \rho_{e0} = - \frac{\mu}{g} \frac{\text{d}p_{e0}}{\text{d}\zeta}, \\ & B_{0z} = r_{0}^{-2} S, \qquad B_{0r} = \mu r r_{0}^{-3} \frac{\text{d}r_{0}}{\text{d}\zeta} S \equiv \mu B_{0r}^{*}. \end{aligned} \end{aligned}$$

(13)

The undisturbed state is hence defined by two arbitrary functions, $r_{0}(\zeta)$ and $p_{0}(\zeta)$, and the constant $S$. Moreover, we assume that

$$\frac{\text{d}p_{0}}{\text{d}\zeta} \sim p_{0}/\mu H, $$

so that the terms of order zero in the expansion of $\rho$ and $\rho_{e}$ in the power series of $\mu$ are $\rho_{0}$ and $\rho_{e0}$.

3 The Governing Equation for Nonlinear Surface MHD Waves

After having defined the undisturbed state using Equations (13), we may now begin deriving the equation that governs the propagation of nonlinear small-amplitude slow sausage MHD waves in the long-wavelength approximation. Since the tube is assumed to be axisymmetric, the variables we deal with depend on $r$ and $z$ only, and the azimuthal component of the velocity and the magnetic induction are zero.

Under the stated assumptions, the motion of the plasma inside the gravitationally stratified and expanding tube may be modelled by the equations of magnetohydrodynamics (MHD):

$$\begin{aligned} \begin{aligned} & \frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \boldsymbol {v} ) = 0, \\ & \frac{\partial}{\partial t} \biggl( \frac{p}{\rho^{\gamma}} \biggr) + \boldsymbol {v} \cdot \nabla \biggl( \frac{p}{\rho^{\gamma}} \biggr) = 0, \\ & \frac{\partial \boldsymbol {v}}{\partial t} + ( \boldsymbol {v} \cdot \nabla ) \boldsymbol {v} = - \frac{1}{\rho} \nabla p + \frac{1}{\mu \rho} (\nabla \times \boldsymbol {B}) \times \boldsymbol {B} + \boldsymbol {g}, \\ & \frac{\partial \boldsymbol {B}}{\partial t} + \nabla \times ( \boldsymbol {v} \times \boldsymbol {B} ) = 0, \\ & \nabla \cdot \boldsymbol {B} = 0. \end{aligned} \end{aligned}$$

(14)

Outside the tube, the motion of the gas is governed by the equations of gas dynamics:

$$\begin{aligned} \begin{aligned} & \frac{\partial \rho_{e}}{\partial t} + \nabla \cdot ( \rho_{e} \boldsymbol {v}_{e}) = 0, \\ & \frac{\partial \boldsymbol {v}_{e}}{\partial t} + (\boldsymbol {v}_{e} \cdot \nabla) \boldsymbol {v}_{e} = - \frac{1}{\rho_{e}} \nabla p_{e} + \boldsymbol {g}, \\ & \frac{\partial}{\partial t} \biggl( \frac{p_{e}}{\rho_{e}^{\gamma}} \biggr) + \boldsymbol {v}_{e} \cdot \nabla \biggl( \frac{p_{e}}{\rho_{e}^{\gamma}} \biggr) = 0. \end{aligned} \end{aligned}$$

(15)

We define the velocity as $\boldsymbol {v} = (u, 0, w)$. The boundary of the tube is defined as $r = r_{0} + \eta$, where $\eta$ is the disturbance of the boundary. Here, the conditions of the continuity of the normal components of the velocity and the magnetic field, as well as the condition of equilibrium of the total pressure, and the kinematic boundary condition must be satisfied. These are

$$\begin{aligned} \begin{aligned} & u - w \frac{\partial (\eta + r_{0})}{\partial z} = u_{e} - w_{e} \frac{\partial (\eta + r_{0})}{\partial z}, \\ & B_{r} - B_{z} \frac{\partial (\eta + r_{0})}{\partial z} = 0, \\ & p + \frac{B^{2}}{2 \mu_{0}} = p_{e}, \qquad u = \frac{\partial \eta}{\partial t} + w \frac{\partial \eta}{\partial z}. \end{aligned} \end{aligned}$$

(16)

Additionally, we assume that all disturbances of any variables should vanish as $|r| \to \infty$.

Let $\epsilon \ll 1$ be the non-dimensional amplitude of the waves. By the thin-tube approximation, we assume that $r_{0}/L \sim \epsilon$, where $L$ is the wavelength. We now introduce a new variable $\tau = \epsilon ( t - \int \mathrm{d}z/c_{T} )$. Hence, the nonlinearity and dispersion significantly influence the wave when it progresses a distance of the order of $\epsilon^{-2}r_{0}$. For the effect of the stratification to be of the same order as the effects of nonlinearity and dispersion, we assume that $\mu = \epsilon^{2}$ in our description of the undisturbed state.

Inside the tube, the horizontal scale is equal to $r_{0}$. Outside it, however, the horizontal and vertical scales are equal to the wavelength. It is therefore advantageous to introduce the new variable $r_{e} = \epsilon r$ to be used outside the tube, instead of $r$.

We now transform the set of MHD equations (14), the set of gas equations (15), and the associated boundary conditions (16) into the new coordinate systems using $r$, $\tau$, $\zeta$, and $r_{e}$, $\tau$, $\zeta$ as appropriate:

$$\begin{aligned} \begin{aligned} & \frac{\partial \rho}{\partial \tau} + \epsilon^{-1} \frac{1}{r} \frac{\partial (r \rho u)}{\partial r} - \frac{1}{c_{T}} \frac{\partial (\rho w)}{\partial \tau} + \epsilon \frac{\partial (\rho w)}{\partial \zeta} = 0, \\ & \epsilon \frac{\partial u}{\partial \tau} + u \frac{\partial u}{\partial r} - \epsilon \frac{w}{c_{T}} \frac{\partial u}{\partial \tau} + \epsilon^{2} w \frac{\partial u}{\partial \zeta} = \\ & \quad = - \frac{1}{\rho} \frac{\partial}{\partial r} \biggl( p + \frac{B_{z}^{2}}{2 \mu_{0}} \biggr) - \frac{B_{z}}{\mu_{0} \rho} \biggl( \frac{\epsilon}{c_{T}} \frac{\partial B_{r}}{\partial \tau} - \epsilon^{2} \frac{\partial B_{r}}{\partial \zeta} \biggr), \\ & \frac{\partial w}{\partial \tau} + \epsilon^{-1} u \frac{\partial w}{\partial r} - \frac{w}{c_{T}} \frac{\partial w}{\partial \tau} + \epsilon w \frac{\partial w}{\partial \zeta} = \\ & \quad = \frac{1}{\rho} \biggl( \frac{1}{c_{T}} \frac{\partial}{\partial \tau} - \epsilon \frac{\partial}{\partial \zeta} \biggr) \biggl( p + \frac{B_{r}^{2}}{2 \mu_{0}} \biggr) + \frac{B_{r}}{\mu_{0} \rho} \epsilon^{-1} \frac{\partial B_{z}}{\partial r} - \epsilon^{-1} g, \\ & \epsilon^{-1} \frac{\partial B_{r}}{\partial \tau} = \epsilon^{-1} \biggl( \frac{1}{c_{T}} \frac{\partial}{\partial \tau} - \epsilon \frac{\partial}{\partial \zeta} \biggr) ( w B_{r} - u B_{z} ), \\ & \frac{\partial B_{z}}{\partial \tau} = \epsilon^{-1} \frac{1}{r} \frac{\partial}{\partial r} \bigl[ r ( w B_{r} - u B_{z} ) \bigr], \\ & \frac{\partial}{\partial \tau} \biggl( \frac{p}{\rho^{\gamma}} \biggr) + \epsilon^{-1} u \frac{\partial}{\partial r} \biggl( \frac{p}{\rho^{\gamma}} \biggr) - \frac{w}{c_{T}} \frac{\partial}{\partial \tau} \biggl( \frac{p}{\rho^{\gamma}} \biggr) + \epsilon w \frac{\partial}{\partial \zeta} \biggl( \frac{p}{\rho^{\gamma}} \biggr) = 0, \\ & \epsilon^{-1} \frac{1}{r} \frac{\partial (B_{r} r)}{\partial r} - \frac{1}{c_{T}} \frac{\partial B_{z}}{\partial \tau} + \epsilon \frac{\partial B_{z}}{\partial \zeta} = 0. \end{aligned} \end{aligned}$$

(17)

Outside the tube, the governing equations become

$$\begin{aligned} \begin{aligned} & \frac{\partial \rho_{e}}{\partial \tau} + \frac{1}{r_{e}} \frac{\partial}{\partial r_{e}}(r_{e} \rho_{e} u_{e}) - \frac{1}{c_{T}} \frac{\partial}{\partial \tau} (\rho_{e} w_{e}) + \epsilon \frac{\partial}{\partial \zeta} (\rho_{e} w_{e}) = 0, \\ & \frac{\partial u_{e}}{\partial \tau} + u_{e} \frac{\partial u_{e}}{\partial r_{e}} - \frac{w_{e}}{c_{T}} \frac{\partial u_{e}}{\partial \tau} + \epsilon w_{e} \frac{\partial u_{e}}{\partial \zeta} = - \frac{1}{\rho_{e}} \frac{\partial p_{e}}{\partial r_{e}}, \\ & \frac{\partial w_{e}}{\partial \tau} + u_{e} \frac{\partial w_{e}}{\partial r_{e}} - \frac{w_{e}}{c_{T}} \frac{\partial w_{e}}{\partial \tau} + \epsilon w_{e} \frac{\partial w_{e}}{\partial \zeta} = \frac{1}{c_{T} \rho_{e}} \frac{\partial p_{e}}{\partial \tau} - \frac{\epsilon}{\rho_{e}} \frac{\partial p_{e}}{\partial \zeta} - g, \\ & \frac{\partial}{\partial \tau} \biggl( \frac{p_{e}}{\rho_{e}^{\gamma}} \biggr) + u_{e} \frac{\partial}{\partial r_{e}} \biggl( \frac{p_{e}}{\rho_{e}^{\gamma}} \biggr) - \frac{w_{e}}{c_{T}} \frac{\partial}{\partial \tau} \biggl( \frac{p_{e}}{\rho_{e}^{\gamma}} \biggr) + \epsilon w_{e} \frac{\partial}{\partial \zeta} \biggl( \frac{p_{e}}{\rho_{e}^{\gamma}} \biggr) = 0. \end{aligned} \end{aligned}$$

(18)

The boundary conditions at $r = r_{0} + \eta$ become

$$\begin{aligned} \begin{aligned} & \epsilon^{-1} u + w \biggl( \frac{1}{c_{T}} \frac{\partial}{\partial \tau} - \epsilon \frac{\partial}{\partial \zeta} \biggr) (r_{0} + \eta) = \epsilon^{-1} u_{e} + w_{e} \biggl( \frac{1}{c_{T}} \frac{\partial}{\partial \tau} - \epsilon \frac{\partial}{\partial \zeta} \biggr) (r_{0} + \eta), \\ & \epsilon^{-1} B_{r} + B_{z} \biggl( \frac{1}{c_{T}} \frac{\partial}{\partial \tau} - \epsilon \frac{\partial}{\partial \zeta} \biggr) (r_{0} + \eta) = 0, \\ & \epsilon^{-1} u = \frac{\partial \eta}{\partial \tau} - w \biggl( \frac{1}{c_{T}} \frac{\partial}{\partial \tau} - \epsilon \frac{\partial}{\partial \zeta} \biggr) (r_{0} + \eta), \qquad p + \frac{B^{2}}{2 \mu_{0}} = p_{e}. \end{aligned} \end{aligned}$$

(19)

We now seek the solution of Equations (17) and (18) with corresponding boundary conditions (19) in the form of expansions in a power series of $\epsilon$. It follows from the related linear theory that the disturbances of $w$, $\rho$, $p$, $B_{z}$, and $\eta$ are of the order of $\epsilon$. We may therefore write the power series for each variable in the form

$$ f = f_{0} + \epsilon f_{1} + \epsilon^{2} f_{2} + \cdots. $$

(20)

The disturbances of $u$, $B_{r}$, $u_{e}$, $w_{e}$, $p_{e}$, and $\rho_{e}$ are of the order of $\epsilon^{2}$, so their power series may be written in the form:

$$ f = f_{0} + \epsilon^{2} f_{1} + \epsilon^{3} f_{2} + \cdots. $$

(21)

Finally, $B_{r}$ is expanded as

$$ B_{r} = \epsilon^{2} \bigl(B_{r0}^{*} + B_{r1} \bigr) + \epsilon^{3} B_{r2}. $$

(22)

We emphasise the fact that because the equilibrium values of the velocity in the undisturbed state are equal to zero, the values of $u_{0}$, $u_{e0}$, $w_{0}$, $w_{e0}$, and $\eta_{0}$ are all equal to zero in their respective expansions.

Let us substitute Equations (20), (21), and (22) into Equations (17), and retain the terms of order $\epsilon$. Taking into account Equations (13) gives

$$\begin{aligned} \begin{aligned} & \frac{\partial \rho_{1}}{\partial \tau} + \frac{1}{r} \rho_{0} u_{1} + \rho_{0} \frac{\partial u_{1}}{\partial r} - \frac{1}{c_{T}} \rho_{0} \frac{\partial w_{1}}{\partial \tau} = 0, \\ & \frac{\partial}{\partial r} \biggl( p_{1} + \frac{B_{z0} B_{z1}}{\mu_{0}} \biggr) = 0, \\ & c_{T} \frac{\partial w_{1}}{\partial \tau} = \frac{1}{\rho_{0}} \frac{\partial p_{1}}{\partial \tau}, \qquad c_{T} \frac{\partial B_{r1}}{\partial \tau} = - B_{z0} \frac{\partial u_{1}}{\partial \tau}, \\ & \frac{\partial B_{z1}}{\partial \tau} = - \frac{1}{r} B_{z0} u_{1} - B_{z0} \frac{\partial u_{1}}{\partial r}, \\ & \frac{\partial p_{1}}{\partial \tau} = c_{0}^{2} \frac{\partial \rho_{1}}{\partial \tau}, \qquad \frac{\partial B_{r1}}{\partial r} - \frac{1}{c_{T}} \frac{\partial B_{z1}}{\partial \tau} + \frac{1}{r} B_{r1} = 0. \end{aligned} \end{aligned}$$

(23)

Taking the terms of the order of $\epsilon$ in the boundary conditions (19) we obtain

$$\begin{aligned} \begin{aligned} \frac{1}{\mu_{0}} B_{z0} B_{z1} + p_{1} = 0, \qquad u_{1} = u_{e1}^{(0)}, \qquad u_{1} = \frac{\partial \eta_{1}}{\partial \tau}, \end{aligned} \end{aligned}$$

(24)

at $r = r_{0}$. We omit rewriting here the condition of the continuity of the magnetic field at the boundary, since it would be equivalent to the fourth of Equations (23).

When deriving Equations (24), we make use of the relation $r_{e} = \epsilon r$ and expand all the outside variables in series around $r_{e} = 0$. This means that, for example, $u_{e}(\epsilon r_{0}) = u_{e}^{(0)} + \epsilon r_{0} (\partial u_{e}/ \partial r_{e})^{(0)} + \cdots$, where the upper zero indices indicate that the variable is taken at $r_{e} = 0$.

Assuming that all disturbances vanish as $\tau \to \infty$ or $\tau \to - \infty$, we may derive a new set of relations from Equations (23), and boundary conditions (24). These are:

$$\begin{aligned} \begin{aligned} & B_{z1} = - B_{z0} \frac{c_{T}}{v_{A}^{2}} w_{1}, \qquad B_{r1} = - \frac{B_{z0}}{c_{T}} u_{1}, \\ & p_{1} = \rho_{0} c_{T} w_{1}, \qquad \rho_{1} = \frac{1}{c_{0}^{2}} \rho_{0} c_{T} w_{1}, \\ & v_{A}^{2} \frac{\partial u_{1}}{\partial r} - c_{T} \frac{\partial w_{1}}{\partial \tau} = - \frac{v_{A}^{2}}{r} u_{1}. \end{aligned} \end{aligned}$$

(25)

It has been shown that, in addition to the surface modes, there is an infinite set of body modes in a magnetic flux tube (Edwin and Roberts 1983). In order to be able to differentiate between surface and body waves, we note that in the case of slow sausage surface MHD waves, $u$ is a linear function of $r$, while in the case of body waves it is a sinusoidal function of $r$. We now suppose that $u_{1}$ is a linear function of $r$, and from (24) we obtain

$$ u_{1} = \frac{r}{r_{0}} \frac{\partial \eta_{1}}{\partial \tau}. $$

(26)

Substituting Equation (26) into the last of Equations (25) and integrating, we find

$$ w_{1} = \frac{2 v_{A}^{2}}{c_{T} r_{0}} \eta_{1}. $$

(27)

Let us take the terms of the order of $\epsilon^{2}$ in Equations (17), in conjunction with Equations (25), (26), and (27) we obtain

$$\begin{aligned} &\frac{\partial \rho_{2}}{\partial \tau} + \rho_{0} \frac{u_{2}}{r} + \rho_{0} \frac{\partial u_{2}}{\partial r} - \frac{\rho_{0}}{c_{T}} \frac{\partial w_{2}}{\partial \tau} \\ & \quad = 4 \rho_{0} v_{A}^{2} \frac{c_{T}^{2} - 2 v_{A}^{2}}{c_{T}^{2} c_{0}^{2} r_{0}^{2}} \eta_{1} \frac{\partial \eta_{1}}{\partial \tau} - \frac{\partial}{\partial \zeta} \biggl( \frac{2 \rho_{0} v_{A}^{2} \eta_{1}}{c_{T} r_{0}} \biggr), \end{aligned}$$

(28)

$$\begin{aligned} & \frac{\partial}{\partial r} \biggl( p_{2} + \frac{B_{z0}B_{z2}}{\mu_{0}} \biggr) = 0, \end{aligned}$$

(29)

$$\begin{aligned} & \frac{\partial w_{2}}{\partial \tau} - \frac{1}{c_{T} \rho_{0}} \frac{\partial p_{2}}{\partial \tau} = 4 v_{A}^{4} \frac{c_{0}^{2} - c_{T}^{2}}{c_{T}^{3} c_{0}^{2} r_{0}^{2}} \eta_{1} \frac{\partial \eta_{1}}{\partial \tau} - \frac{1}{\rho_{0}} \frac{\partial}{\partial \zeta} \biggl( \frac{2 \rho_{0} v_{A}^{2} \eta_{1}}{r_{0}} \biggr) + \frac{2 v_{A}^{2} \eta_{1}}{\rho_{0} c_{0}^{2} r_{0}} \frac{\mathrm{d} p_{0}}{\mathrm{d} \zeta}, \\ & \frac{\partial B_{r2}}{\partial \tau} + \frac{B_{z0}}{c_{T}} \frac{\partial u_{2}}{\partial \tau} = - rB_{z0} \frac{2 v_{A}^{2} - c_{T}^{2}}{c_{T}^{3} r_{0}^{2}} \frac{\partial}{\partial \tau} \biggl( \eta_{1} \frac{\partial \eta_{1}}{\partial \tau} \biggr) + r \frac{\partial}{\partial \zeta} \biggl( \frac{B_{z0}}{r_{0}} \frac{\partial \eta_{1}}{\partial \tau} \biggr), \\ & \frac{\partial B_{z2}}{\partial \tau} + B_{z0} \frac{u_{2}}{r} + B_{z0} \frac{\partial u_{2}}{\partial r} = - 4B_{z0} \frac{v_{A}^{2} - c_{T}^{2}}{c_{T}^{2} r_{0}^{2}} \eta_{1} \frac{\partial \eta_{1}}{\partial \tau} + \frac{4 v_{A}^{2} \eta_{1}}{c_{T} r_{0}} \frac{\partial B_{r0}^{*}}{\partial r}, \end{aligned}$$

(30)

$$\begin{aligned} & \frac{\partial p_{2}}{\partial \tau} - c_{0}^{2} \frac{\partial \rho_{2}}{\partial \tau} = \frac{4(\gamma - 1) \rho_{0} v_{A}^{4}}{c_{0}^{2} r_{0}^{2}} \eta_{1} \frac{\partial \eta_{1}}{\partial \tau} - \frac{2 v_{A}^{2} \eta_{1}}{c_{T} r_{0}} \biggl( \frac{\mathrm{d} p_{0}}{\mathrm{d} \zeta} - c_{0}^{2} \frac{\mathrm{d} \rho_{0}}{\mathrm{d} \zeta} \biggr), \\ & \frac{\partial B_{r2}}{\partial r} + \frac{B_{r2}}{r} - \frac{1}{c_{T}} \frac{\partial B_{z2}}{\partial \tau} = - \frac{\partial B_{z0}}{\partial \zeta}. \end{aligned}$$

(31)

We also take the terms of the order of $\epsilon^{2}$ in the boundary condition for the total pressure:

$$ p_{2} + \frac{B_{z0} B_{z2}}{\mu_{0}} = p_{e1}^{(0)} - \frac{2 \rho_{0} v_{A}^{2}}{r_{0}^{2}} \eta_{1}^{2} \quad \text{at } r = r_{0}. $$

(32)

It follows from Equation (29) that Equations (32) are satisfied everywhere inside the flux tube. We must now find a way to express $\rho_{2}$, $p_{2}$ and $u_{2}$ in the above equations in terms of $w_{2}$, $\eta_{1}$, and $p_{e1}^{(0)}$. Using Equations (28)–(32) we arrive at

$$\begin{aligned} \begin{aligned} & \frac{\partial \eta_{1}}{\partial \zeta} - a \eta_{1} \frac{\partial \eta_{1}}{\partial \tau} + \frac{\eta_{1}}{2b} \frac{\mathrm{d} b}{\mathrm{d} \zeta} - \frac{c_{T} r_{0}}{4 \rho_{0} v_{A}^{4}} \frac{\partial p_{e1}^{(0)}}{\partial \tau} = 0, \\ & a = \frac{c_{T}}{c_{0}^{4} r_{0}} \bigl[ 3c_{0}^{2} + (\gamma + 1) v_{A}^{2} \bigr], \qquad b = \frac{\rho_{0} v_{A}^{4}}{c_{T}}. \end{aligned} \end{aligned}$$

(33)

The only task left now is that of expressing $p_{e1}$ in terms of $\eta_{1}$. In order to do so we consider the terms of the order of $\epsilon^{2}$ in Equations (18):

$$\begin{aligned} \begin{aligned} & \frac{\partial \rho_{e1}}{\partial \tau} + \frac{\rho_{e0} u_{e1}}{r_{e}} + \rho_{e0} \frac{\partial u_{e1}}{\partial r_{e}} - \frac{\rho_{e0}}{c_{T}}\frac{\partial w_{e1}}{\partial \tau} = 0, \\ & \frac{\partial u_{e1}}{\partial \tau} = - \frac{1}{\rho_{e0}} \frac{\partial p_{e1}}{\partial r_{e}}, \\ & w_{e} = \frac{1}{c_{T} \rho_{e0}} p_{e1}, \\ & p_{e1} = c_{e}^{2} \rho_{e1}. \end{aligned} \end{aligned}$$

(34)

Eliminating all other variables in favour of $p_{e1}$ yields

$$\begin{aligned} \begin{aligned} & \frac{\partial^{2} p_{e1}}{\partial r_{e}^{2}} + \frac{1}{r_{e}} \frac{\partial p_{e1}}{\partial r_{e}} + q^{2} \frac{\partial^{2} p_{e1}}{\partial \tau^{2}} = 0. \\ & q^{2} = \frac{c_{e}^{2} - c_{T}^{2}}{c_{e}^{2} c_{T}^{2}}. \end{aligned} \end{aligned}$$

(35)

The boundary condition for Equation (25) is derived using Equations (24) and (34):

$$ \frac{\partial p_{e1}}{\partial r_{e}} = - \rho_{e0} \frac{\partial^{2} \eta_{1}}{\partial \tau^{2}} \quad \text{at } r_{e} = \epsilon r_{0}. $$

(36)

Fourier transforming Equations (35) and (36) with respect to $\tau$ yields

$$\begin{aligned} \begin{aligned} & r_{e}^{2} \frac{\partial^{2} \hat{p}_{e1}}{\partial r_{e}^{2}} + r_{e} \frac{\partial \hat{p}_{e1}}{\partial r_{e}} - r_{e}^{2} \omega^{2} q^{2} \hat{p}_{e1} = 0, \\ & \frac{\partial \hat{p}_{e1}}{\partial r_{e}} = - \rho_{e0} \omega^{2} \hat{ \eta}_{1}, \quad \text{at } r_{e} = \epsilon r_{0}. \end{aligned} \end{aligned}$$

(37)

Taking the solution of Equation (37) at $r_{e} = \epsilon r_{0}$ gives

$$ \hat{p}_{e1}^{(0)} = - \frac{\rho_{e0}}{q} \frac{ \omega K_{0} (q \omega \epsilon r_{0})}{K_{1} (q \omega \epsilon r_{0} )} \hat{\eta}_{1}. $$

(38)

Using the Fourier inversion theorem, and the convolution theorem, and after making the suitable variable transformations, we write $p_{e1}^{(0)}$ as

$$\begin{aligned} \begin{aligned} & p_{e1}^{(0)} = \frac{\rho_{e0}}{2q} \frac{\partial^{2}}{\partial \tau^{2}} \mathscr{C}(\eta_{1}), \\ & \mathscr{C}(\eta_{1}) = \int_{-\infty}^{\infty} F\bigl( \epsilon^{-1} q^{-1} r_{0}^{-1}\bigl(\tau - \tau' \bigr)\bigr) \eta_{1}\bigl(\zeta, \tau'\bigr)\, \mathrm{d} \tau', \\ & F(\tau) = \frac{2}{\pi} \int_{0}^{\infty} \frac{K_{0} (\omega) \cos(\omega \tau)}{\omega K_{1} (\omega)}]\, \mathrm{d}\omega. \end{aligned} \end{aligned}$$

(39)

Let us now substitute Equation (39) into Equation (33) in order to obtain

$$ \frac{\partial \eta_{1}}{\partial \zeta} - a \eta_{1} \frac{\partial \eta_{1}}{\partial \tau} + \frac{\eta_{1}}{2b} \frac{\mathrm{d} b}{\mathrm{d} \zeta} - \frac{\delta r_{0}}{4 c_{T}^{2}} \frac{\partial^{3}}{\partial \tau^{3}} \mathscr{C}(\eta_{1}) = 0, $$

(40)

where

$$\delta = \frac{\rho_{e0} c_{e} c_{T}^{4}}{2 \rho_{0} v_{A}^{4} (c_{e}^{2} - c_{T}^{2})^{1/2} }. $$

Taking $\eta \approx \epsilon \eta_{1}$, and returning to the initial variables, the governing equation for the stratified atmosphere becomes

$$\begin{aligned} & \frac{\partial \eta}{\partial z} + \frac{1}{c_{T}} \frac{\partial \eta}{\partial t} - a \eta \frac{\partial \eta}{\partial t} - \frac{\delta r_{0}}{4 c_{T}^{2}} \frac{\partial^{3}}{\partial t^{3}} \mathscr{C}(\eta) + \eta \frac{1}{2 b}\frac{\mathrm{d} b}{\mathrm{d} z} = 0, \\&\quad \mathscr{C}(\eta) = \int_{-\infty}^{\infty} F\bigl(q^{-1} r_{0}^{-1}\bigl(t - t'\bigr)\bigr) \eta_{1}\bigl(z, t'\bigr)\, \mathrm{d}t'. \end{aligned}$$

(41)

Equation (41) describes the propagation of nonlinear, small-amplitude, long-wavelength slow sausage MHD waves along an expanding magnetic cylinder in a field-free environment under the influence of three competing effects: nonlinearity, dispersion, and stratification (described by the final term in the equation).

4 Numerical Investigation

The initial value problem for Equation (41) was first solved numerically by Leibovich and Randall (1972). When doing so, they used a simplified version of the equation which we will now address briefly.

In their analysis, Leibovich and Randall (1972) did not discuss the convergence of the solitary wave solution to the Leibovich–Roberts equation. Molotovshchikov and Ruderman (1987) resolved this problem by finding a solitary wave solution which converges quickly, using the Petviashvili method (Petviashvili 1976). We will employ this method here to obtain solutions to Equation (41). First, let us make the substitutions $\eta = b^{-1/2} \Phi$, and $t = \theta + \int \mathrm{d}z/c_{T}$, so that Equation (41) becomes

$$ \frac{\partial \Phi}{\partial z} - \frac{a}{b^{1/2}} \Phi \frac{\partial \Phi}{\partial \theta} - \frac{\delta r_{0}}{4 c_{T}^{2}} \frac{\partial^{3}}{\partial \theta^{3}} \mathscr{C}(\Phi) = 0. $$

(42)

To further simplify, we introduce the independent variable $\sigma = \int \mathrm{d}z a b^{-1/2}$, and multiply the obtained equation by $b^{1/2}/a$. Equation (42) then becomes

$$ \frac{\partial \Phi}{\partial \sigma} - \Phi \frac{\partial \Phi}{\partial \theta} - \frac{\delta r_{0} b^{1/2}}{4 c_{T}^{2} a} \frac{\partial^{3}}{\partial \theta^{3}} \mathscr{C}(\Phi) = 0. $$

(43)

We now search for the solutions of Equation (43) that depend on $y = q^{-1} r_{0}^{-1}(2 \theta - V \sigma)$. Equation (43) reduces to

$$\begin{aligned} \begin{aligned} & V \Phi + \Phi^{2} + \psi \frac{\partial^{2}}{\partial y^{2}} \mathscr{C}(\Phi) = 0, \\ & \mathscr{C} \bigl(\Phi(y) \bigr) = \int_{-\infty}^{\infty} F \bigl(y - y' \bigr) \Phi \bigl(y' \bigr)\, \mathrm{d}y', \\ & \psi = \frac{2 c_{e}^{3} c_{0}^{4} c_{T}^{5/2} \rho_{e0}}{v_{A}^{2} \rho_{0}^{1/2} (c_{e}^{2} - c_{T}^{2})^{3/2} [ 3 c_{0}^{2} + (\gamma + 1) v_{A}^{2}]}. \end{aligned} \end{aligned}$$

(44)

When deriving Equation (44), we integrated with respect to $y$ and took into account the fact that $\Phi \to 0$ as $|y| \to \infty$.

For ease of computation, we assume that $\psi$ is constant, and apply the numerical scheme for several values of $\psi$ so that we may see how the shape of the wave is impacted by the level of stratification. We take the Fourier transform of Equation (44), where ℱ denotes the Fourier transform, and $k$ is the transformed variable $y$. Furthermore, applying the convolution theorem will yield the equation

$$V \hat{\Phi} + \hat{\Phi^{2}} - \psi k^{2} \hat{F}(k) \hat{ \Phi} = 0, $$

where $\hat{F}(k)$ is the Fourier transform of the integral function $F(y)$. This equation may now be rearranged as

$$\hat{\Phi} \bigl[V + \psi k^{2} \hat{F}(k)\bigr] = \hat{ \Phi^{2}} = \frac{1}{2 \pi} \int_{-\infty}^{\infty}\hat{\Phi}\bigl(k'\bigr) \hat{\Phi}\bigl(k' - k\bigr) \,\mathrm{d}k'. $$

We may now define $\Phi$ in terms of two new functions

$$\begin{aligned} \begin{aligned} \hat{\Phi}(k) & = G(k) \Pi(k), \quad G(k) = \bigl\{ V + \psi k^{2} \hat{F}(k) \bigr\} ^{-1}, \\ \Pi(k) & = \frac{1}{2 \pi} \int_{-\infty}^{\infty}\hat{\Phi}\bigl(k'\bigr) \hat{\Phi}\bigl(k' - k\bigr)\, \mathrm{d}k', \end{aligned} \end{aligned}$$

(45)

and further write $G(k)$ explicitly as

$$G(k) = \bigl\{ V + 2 \psi |k| K_{0}\bigl(|k|\bigr) K_{1}\bigl(|k|\bigr)^{-1} \bigr\} ^{-1}. $$

When doing so, we find that $G(k)$ is finite for any $k$ provided that $V > 0$, and also that $G(k) \to 0$ at $k \to \infty$. All conditions needed for applying the Petviashvili method are thus satisfied.

Following Molotovshchikov and Ruderman (1987), we rearrange Equation (45) such that it becomes

$$\begin{aligned} &\hat{\Phi}(k) = \biggl( \frac{s_{1}}{s_{2}} \biggr)^{2} G(k) \Pi(k), \\ &\quad s_{1} = \int_{-\infty}^{\infty}\Phi^{2}(k) \mathrm{d}k, \ s_{2} = \int_{-\infty}^{\infty}\Phi(k) G(k) \Pi(k) \mathrm{d}k. \end{aligned}$$

(46)

It is immediately visible that Equations (45) and (46) are equivalent, meaning that any solution of one is also a solution of the other. We proceed to solve Equation (46) using the iterative method defined such that the $(n+1)$th term is related to the $n$th by the formula

$$\hat{\Phi}_{n+1} = \biggl( \frac{s_{1n}}{s_{2n}} \biggr)^{2} G \Pi_{n}. $$

We implement the iterative method, using $\hat{\Phi}_{1} = \exp(-|k|)$ as a first approximation, and halt it provided that

$$\text{max} \biggl\vert \frac{\hat{\Phi}_{n+1} - \hat{\Phi}_{n}}{\hat{\Phi}_{n+1}} \biggr\vert < 10^{-3}. $$

The sequence $\{ \hat{\Phi} \}$ then rapidly converges, with $s_{1n}/s_{2n} \to 1$.

The results obtained by Molotovshchikov and Ruderman (1987) are similar to our own computations. This is due to the fact that the equation in Molotovshchikov and Ruderman (1987) may be reduced to Equation (44) when the parameter $\psi$ is equal to one.

The results of the numerical calculations are presented in Figures 2–7. Figure 2 illustrates the shape of the solitary wave solutions of Equation (44), computed for the same value of the parameter $\psi$, while decreasing the value of the speed $V$. We find that the amplitude of the wave decreases sharply, and it is directly proportional to the speed. Such a behaviour is expected when studying the propagation of solitary waves.

Figure 2

Three examples of solitary wave shape computed for $\psi = 2$, and various values of the parameter $V$.

Figure 3 illustrates the different shapes of the solitary wave solutions, for a constant value of $V$, and ascending values of the term describing stratification, $\psi$. We observe that, with greater values of the parameter $\psi$, one obtains waves of larger width, and slightly lower amplitude.

Figure 3

This figure illustrates the dependence of the solitary wave computed for $V=2$ on the parameter $\psi$.

In Figure 4, the dependence of the wave width $D$ to the amplitude $a$, where $\Phi(D/2) = a/2$ and $a = \Phi(0)$, is shown to be of similar nature to that of the Benjamin–Ono soliton. We also note that the level of dependence is in-between that of the Benjamin–Ono soliton and the Korteweg–de Vries soliton.

Figure 4

The dependence of the solitary wave width $D$ on the amplitude $a$. From top to bottom, the lines correspond to the Benjamin–Ono soliton, the solitary wave solution obtained in the present work, and the Korteweg–de Vries soliton, respectively.

Figure 5 builds on Figure 2 and depicts the dependence of the wave amplitude $a$ on the speed $V$ for different values of the stratification parameter $\psi$. We find that the speed is almost linearly dependent on the amplitude, with greater values of $\psi$ forcing lower values of the amplitude, while also making the dependence more nearly linear.

Figure 5

The dependence of the solitary wave amplitude $a$ on the speed $V$ for different values of the parameter $\psi$.

In Figure 6, we observe how the width $D$ of the solitary wave is affected by an increase in the parameter $\psi$, for different values of $V$. We note that smaller values of $V$ correspond to steeper growth of the width $D$ as $\psi$ increases. We also note that the growth appears to be parabolic, similar to that of a square root function.

Figure 6

The dependence of the solitary wave width $D$ on the stratification parameter $\psi$, plotted for different values of $V$.

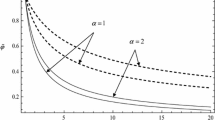
Finally, Figure 7 presents the dependence of the amplitude on the parameter $\psi$, for different values of $V$. The vertical dashed line marks the point where $\psi = 1$, which represents the case where stratification is absent. The horizontal dashed lines are approximate asymptotes for the amplitude $a$, for each respective value of $V$.

Figure 7

The dependence of the solitary wave amplitude with respect to the stratification parameter $\psi$, plotted for different values of $V$.

5 Conclusion

The propagation of long-wavelength small-amplitude slow MHD sausage waves in expanding magnetic flux tubes in a field-free environment, with the effects due to gravity taken into account, is modelled by Equation (41).

It should be noted that in this case the tube is not of constant width, being stratified, and expanding due to the effects of gravity. The vertical gravitational stratification is represented in Equation (41) by the final term. Waves propagating along the tube will therefore be under the influence of three competing effects: nonlinearity, dispersion, and stratification. We have therefore proven that if these three effects are of the same order, a soliton may form and propagate stably.

All of these properties are relevant to the study of coronal heating due to the innate properties of solitons, such as energy conservation during propagation. This makes solitons prime candidates as a possible energy transfer mechanism from the photosphere into the lower atmosphere.

The thin flux tube approximation imposes the condition that $r_{0} \ll H$, which suggests that, for a photospheric scale height of $H \approx 200~\mbox{km}$, we may expect a tube radius of $r_{0} \lesssim 50~\mbox{km}$ at the base.

To illustrate an application of the theory, we choose the following values typical to the photosphere: $v_{A} = 10~\mbox{km}\,\mbox{s}^{-1}$, $c_{e} = c_{0} = 8~\mbox{km}\,\mbox{s}^{-1}$, $\gamma = \frac{5}{3}$, $\rho_{0} = 5 \times 10^{-3}~\mbox{kg}\,\mbox{m}^{-3}$, and a density ratio of $\rho_{e0}/\rho_{0} = 0.9$, which yield a wave amplitude of $\eta \approx 3~\mbox{km}$. In contrast, choosing values typical to the base of the corona, $v_{A} = 3000~\mbox{km}\,\mbox{s}^{-1}$, $c_{e} = c_{0} = 200~\mbox{km}\,\mbox{s}^{-1}$, $\gamma = \frac{5}{3}$, $\rho_{0} = 1 \times 10^{-10}~\mbox{kg}\,\mbox{m}^{-3}$, and a density ratio of $\rho_{e0}/\rho_{0} = 0.9$, the amplitude of the wave will increase to $\eta \approx 24~\mbox{km}$.

Further work may include the numerical calculation of the typical energy of such solitary waves in the photosphere, the distance a disturbance would need to travel before the various forces balance out and a soliton forms, or the interaction of several solitary waves in order to confirm that their properties conform to those of solitons.