Abstract
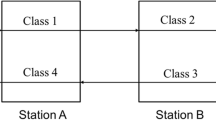
While many single station queues possess explicit forms for their equilibrium probabilities, queueing networks are more problematic. Outside of the class of product form networks (e.g., Jackson, Kelly, and BCMP networks), one must resort to bounds, simulation, asymptotic studies or approximations. By focusing on a class of two-station closed reentrant queueing networks under the last buffer first served (LBFS) policy, we show that non-product form equilibrium probabilities can be obtained. When the number of customer classes in the network is five or fewer, explicit solutions can be obtained. Otherwise, we require the roots of a characteristic polynomial and a matrix inversion that depend only on the network topology. The approach relies on two key points. First, under LBFS, the state space can be reduced to four dimensions independent of the number of buffers in the system. Second, there is a sense of spatial causality in the global balance equations that can then be exploited.
To our knowledge, these two-station closed reentrant queueing networks under LBFS represent the first class of queueing networks for which explicit non-product form equilibrium probabilities can be constructed (for five customer classes or less), the generic form of the equilibrium probabilities can be deduced and matrix analytic approaches can be applied. As discussed via example, there may be other networks for which related observations can be exploited.




Similar content being viewed by others
References
Jackson, J.R.: Jobshop-like queueing systems. Manag. Sci. 10(1), 131–142 (1963)
Kelly, F.P.: Reversibility and Stochastic Networks. Wiley, Chichester (1979)
Baskett, F., Chandy, K.M., Muntz, R.R., Palacios, F.G.: Open, closed and mixed networks of queues with different classes of customers. J. ACM 22(2), 248–260 (1975)
Balsamo, S.: Product form queueing networks. In: Haring, G., Lindemann, C., Reiser, M. (eds.) Performance Evaluation: Origins and Directions. LNCS, vol. 1969, pp. 377–401. Springer, Berlin (2000).
Harrison, J.M., Williams, R.J.: Brownian models of feedforward queueing networks: quasireversibility and product form solutions. Ann. Appl. Probab. 2(2), 263–293 (1992)
Mather, W.H., Hasty, J., Tsimring, L.S., Williams, R.J.: Factorized time-dependent distributions for certain multiclass queueing networks and an application to enzymatic processing networks. Queueing Syst. 69, 313–328 (2011)
Henderson, W., Taylor, P.G.: Product form in networks of queues with batch arrivals and batch services. Queueing Syst. 6, 77–88 (1990)
Visschers, J., Adan, I., Weiss, G.: A product form solution to a system with multi-type jobs and multi-type servers. Eurandom report 2011-002 (2011)
Adan, I., Weiss, G.: A loss system with skill based servers under assign to longest idle server policy. Eurandom report 2011-042 (2011)
Boucherie, R.J., van Dijk, N.M.: On the arrival theorem for product form queueing networks with blocking. Perform. Eval. 29, 155–176 (1997)
Pittel, B.: Closed exponential networks of queues with saturation: the Jackson-type stationary distribution and its asymptotic analysis. Math. Oper. Res. 4, 357–378 (1979)
Bayer, N., Boucherie, R.J.: On the structure of the space of geometric product-form models. Probab. Eng. Inf. Sci. 16, 241–270 (2002)
Kumar, S., Kumar, P.R.: Performance bounds for queueing networks and scheduling policies. IEEE Trans. Autom. Control AC-39, 1600–1611 (1994)
Bertsimas, D., Paschalidis, I.C., Tsitsiklis, J.N.: Optimization of multiclass queueing networks: polyhedral and nonlinear characterizations of achievable performance. Ann. Appl. Probab. 4, 43–75 (1994)
Morrison, J.R., Kumar, P.R.: New linear program performance bounds for queueing networks. J. Optim. Theory Appl., A Volume in Honor of Professor Y.C. Ho 100(3), 575–597 (1999)
Morrison, J.R., Kumar, P.R.: New linear program performance bounds for closed queueing networks. Discrete Event Dyn. Syst. 11, 291–317 (2001)
Morrison, J.R., Kumar, P.R.: Computational performance bounds for Markov chains with applications. IEEE Trans. Autom. Control 53(5), 1306–1311 (2008)
Russell, M.C., Fraser, J., Rizzo, S., Veatch, M.H.: Comparing LP bounds for queueing networks. IEEE Trans. Autom. Control 54(11), 2703–2707 (2009)
Rizzo, S., Veatch, M.H.: Performance bounds and differential cost approximations for queueing networks. Working paper (2008)
Hopp, W.J., Spearman, M.L.: Factory Physics: Foundations of Manufacturing Management, 2nd edn. McGraw-Hill, New York (2001)
Morrison, J.R., Martin, D.P.: Practical extensions to cycle time approximations for the G/G/m queue with applications. IEEE Trans. Autom. Sci. Eng. 4(4), 523–532 (2007)
Whitt, W.: The queueing network analyzer. Bell Syst. Tech. J. 62(9), 2279–2815 (1983)
Wein, L.M.: Scheduling semiconductor wafer fabrication. IEEE Trans. Semicond. Manuf. 1(3), 115–130 (1988)
Kumar, P.R., Meyn, S.P.: Stability of queueing networks and scheduling policies. IEEE Trans. Autom. Control 40(2), 251–260 (1995)
Dai, J.G., Weiss, G.: Stability and instability of fluid models for reentrant lines. Math. Oper. Res. 21(1), 115–134 (1996)
Hasenbein, J.J.: Necessary conditions for global stability of multiclass queueing networks. Oper. Res. Lett. 21, 87–94 (1997)
Harrison, J.M., Wein, L.M.: Scheduling networks of queues: heavy traffic analysis of a simple open network. Queueing Syst. 5, 265–280 (1989)
Kumar, S., Kumar, P.R.: Queueing network models in the design and analysis of semiconductor wafer fabs. IEEE Transactions on Robotics and Automation 17(5) (2001)
Koenigsberg, E.: Twenty five years of cyclic queues and closed queue networks: a review. J. Oper. Res. Soc. 33, 605–619 (1982)
Taylor, J., Jackson, R.R.P.: An application of the birth and death process to the provision of spare machines. Oper. Res. Q. 5, 96–108 (1954)
Koenigberg, E.: An operations research approach to mine haulage. Min. Congr. J. Pt 1, 64–68 (1959)
Roeder, T.M., Govind, N., Schruben, Lee W.: A queueing network approximation of semiconductor automated material handling system: how much information do we really need? In: Proceedings of the 36th Winter Simulation, pp. 1956–1961 (2004)
Spearman, M.L., Zazanis, M.A.: Push and pull production systems: issues and comparisons. Oper. Res. 40(3), 521–532 (1992)
Kleinrock, L.: Queueing Systems, Computer Applications, vol. II, Wiley, New York (1976)
Morrison, J.R., Kumar, P.R.: A counterexample to a conjecture of Harrison and Wein. In: Proceedings of the 37th IEEE Conference on Decision and Control (1998)
Jung, S., Morrison, J.R.: Closed form solutions for the equilibrium probability distribution in the closed Lu–Kumar network under two buffer priority policies. In: Proceeding of the 8th IEEE International Conference on Control and Automation, pp. 1488–1495 (2010)
Kim, W.-s., Morrison, J.R.: On equilibrium probabilities in a class of two station closed queueing network. In: Proceeding of the International Conference on Control, Automation and System (ICCAS 2010), pp. 237–242 (2010)
Harrison, J.M., Wein, L.M.: Scheduling networks of queues: heavy traffic analysis of a two-station closed network. Oper. Res. 38(6), 1052–1064 (1990)
Kumar, S.: Two-server closed networks in heavy traffic: diffusion limits and asymptotic optimality. Ann. Appl. Probab. 10(3), 930–961 (2000)
Dai, J.G., Vande Vate, J.H.: The stability of two-station multitype fluid networks. Oper. Res. 48(5), 721–744 (2000)
Morrison, J.R., Kumar, P.R.: On the guaranteed throughput and efficiency of closed reentrant lines. Queueing Syst. 28, 33–54 (1998)
Dai, J.G., Hasenbein, J.J., Vande Vate, J.H.: Stability and instability of a two-station queueing network. Ann. Appl. Probab. 14(1), 326–377 (2004)
Latouche, G., Ramaswami, V.: Introduction to Matrix Analytic Methods in Stochastic Modeling. ASA-SIAM Series on Statistics and Applied Probability (1999)
Lippman, S.: Applying a new device in the optimization of exponential queueing systems. Oper. Res. 23, 687–710 (1975)
Kim, M.H., Sutherland, S.: Polynomial root-finding algorithms and branched covers. SIAM J. Comput. 23, 477–486 (1994)
Mahoney, J.F., Sivazlian, B.D.: Partial fractions expansion: a review of computational methodology and efficiency. J. Comput. Appl. Math. 9, 247–269 (1983)
Jin, H., Ou, J., Kumar, P.R.: The throughput of irreducible closed Markovian queueing networks: functional bounds, asymptotic loss, efficiency and the Harrison–Wein conjectures. Math. Oper. Res. 22, 886–920 (1997)
Ross, S.: Stochastic Processes, Wiley, New York (1983)
Lay, D.C.: Linear Algebra and Its Application, 2nd edn. Addison-Wesley, Reading (1997)
Cadzow, J.A.: Discrete Time Systems. Prentice-Hall, Englewood Cliffs (1973)
Ye, J., Li, S.Q.: Folding algorithm: a computational method for finite QBD processes with level-dependent transitions. IEEE Trans. Commun. 42(2), 625–639 (1994)
Acknowledgements
This work was supported in part by Korea Research Foundation (KRF) Grant 20110005696. The authors are grateful for the insightful and helpful comments of the reviewers and editorial team. The paper is much improved for their guidance.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Global balance equations
Here, we obtain the matrix form of the global balance equations and introduce matrix notation omitted in the paper. Similarly to floor 0, we obtain the GBE matrix form for floor 1 as

where

for i=1,…,n−1,

All A i , B i , and C 1’s are m×m matrices. Note that assuming we know the initial conditions Y[−1], Y[1] can be written as Y[1]=S Y[−1] for an appropriate matrix S. Similarly, the general equations for the GBEs can obtained as

2≤k≤N−2, where A i , B i and C 1 are as before.
Letting

We obtain

Appendix B: Matrix definitions for the transition probability matrix
Here, we give notation for the sub-matrices within the transition probability matrix. For convenience, we append virtual states to floors −1 and N−1, so that they too have mn states. Transitions to and from these states occur with probability 0. We can express the transition probability matrix T as

The matrix \(P_{00}^{\prime}\) and Θs are m×m matrices.

Rights and permissions
About this article
Cite this article
Kim, Ws., Morrison, J.R. Non-product form equilibrium probabilities in a class of two-station closed reentrant queueing networks. Queueing Syst 73, 317–339 (2013). https://doi.org/10.1007/s11134-012-9310-1
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11134-012-9310-1