Skip to main content
SpringerLink
Log in

A posteriori error estimations of the Petrov-Galerkin methods for fractional Helmholtz equations

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

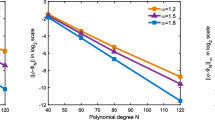
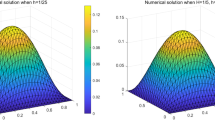
Here, we develop a Petrov-Galerkin spectral method for the fractional Helmholtz equations (FHEs) of even order ν = s + k,s ∈ (k − 1,k) and k ∈ℕ. We define trial and test functions by related generalized Jacobi functions (GJFs). Moreover, we efficiently establish the well-posedness of problem and provide the rigorous priori error estimates. Furthermore, by auxiliary equation, we also obtain the super-approximation estimates. Notably, we propose a post-processing technique for the Petrov-Galerkin spectral method, and give the error estimates of corrected solution. In addition, we define a posteriori error estimators, and prove that they are asymptotically accurate. Finally, we demonstrate the sharpness of our error estimates by numerical experiments.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Du, Q., Gunzburger, M., Lehoucq, R.B., Zhou, K.: Analysis and approximation of nonlocal diffusion problems with volume constraints. SIAM. Rev. 54(4), 667–696 (2012)

    Article  MathSciNet  Google Scholar 

  2. Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: heory and applications of fractional differential equations, vol. 204. Elsevier Science Limited (2006)

  3. Jin, B., Lazarov, R., Zhou, Z.: A Petrov-Galerkin finite element method for fractional convection-diffusion equations. SIAM J. Numer. Anal. 54(1), 481–503 (2016)

    Article  MathSciNet  Google Scholar 

  4. Yang, Y., Chen, Y., Huang, Y., Wei, H.: Spectral collocation method for the time-fractional diffusion-wave equation and convergence analysis. Comput. Math. Appl. 73(6), 1218–1232 (2017)

    Article  MathSciNet  Google Scholar 

  5. Das, P., Rana, S., Ramos, H.: A perturbation-based approach for solving fractional-order Volterra-Fredholm integro differential equations and its convergence analysis. Int. J. Comput. Math. 97(10), 1994–2014 (2020)

    Article  MathSciNet  Google Scholar 

  6. Das, P., Rana, S., Ramos, H.: On the approximate solutions of a class of fractional order nonlinear Volterra integro-differential initial value problems and boundary value problems of first kind and their convergence analysis. J. Comput. Appl. Math. https://doi.org/10.1016/j.cam.2020.113116 (2020)

  7. Das, P., Rana, S.: Theoretical prospects of fractional order weakly singular volterra integro differential equations and their approximations with convergence analysis. Math. Methods Appl. Sci. https://doi.org/10.1002/mma.7369 (2021)

  8. Das, P.: Comparison of a priori and a posteriori meshes for singularly perturbed nonlinear parameterized problems. J. Comput. Appl. Math. 290, 16–25 (2015)

    Article  MathSciNet  Google Scholar 

  9. Tadjeran, C., Meerschaert, M.M.: A second-order accurate numerical method for the two-dimensional fractional diffusion equation. J. Comput. Phys. 220(2), 813–823 (2007)

    Article  MathSciNet  Google Scholar 

  10. Ervin, V.J., Heuer, N., Roop, J.P.: Numerical approximation of a time dependent, nonlinear, space-fractional diffusion equation. SIAM J. Numer. Anal. 45(2), 572–591 (2007)

    Article  MathSciNet  Google Scholar 

  11. Jin, B., Lazarov, R., Zhou, Z.: Error estimates for a semidiscrete finite element method for fractional order parabolic equations. SIAM J. Numer. Anal. 51(1), 445–466 (2013)

    Article  MathSciNet  Google Scholar 

  12. Li, X., Xu, C.: A space-time spectral method for the time fractional diffusion equation. SIAM J. Numer. Anal 47(3), 2108–2131 (2009)

    Article  MathSciNet  Google Scholar 

  13. Li, X., Xu, C.: Existence and uniqueness of the weak solution of the space-time fractional diffusion equation and a spectral method approximation. Commun. Comput. Phys 8(5), 1016 (2010)

    Article  MathSciNet  Google Scholar 

  14. Zayernouri, M., Karniadakis, G.E.: Fractional sturm-liouville eigen-problems: theory and numerical approximation. J. Comput. Phys. 252(1), 495–517 (2013)

    Article  MathSciNet  Google Scholar 

  15. Zayernouri, M., Karniadakis, G.E.: Discontinuous spectral element methods for time- and space-fractional advection equations. SIAM J. Sci. Comput. 36(4), B684–B707 (2014)

    Article  MathSciNet  Google Scholar 

  16. Zayernouri, M., Karniadakis, G.E.: A Petrov-Galerkin spectral element method for fractional elliptic problems. Comput. Method. Appl. M. 324, 512–536 (2017)

    Article  MathSciNet  Google Scholar 

  17. Song, F., Xu, C.: Spectral direction splitting methods for two-dimensional space fractional diffusion equations. J. Comput. Phys. 299, 196–214 (2015)

    Article  MathSciNet  Google Scholar 

  18. Chen, S., Shen, J., Wang, L.: Generalized Jacobi functions and their applications to fractional differential equations. Math. Comput. 85(300), 1603–1638 (2016)

    Article  MathSciNet  Google Scholar 

  19. Mao, Z., Chen, S., Shen, J.: Efficient and accurate spectral method using generalized Jacobi functions for solving riesz fractional differential equations. Appl. Numer. Math. 106, 165–181 (2016)

    Article  MathSciNet  Google Scholar 

  20. Das, P., Natesan, S.: Richardson extrapolation method for singularly perturbed convection-diffusion problems on adaptively generated mesh. Cmes-Comp. Model. Eng. Sci. 90(6), 463–485 (2013)

    MathSciNet  MATH  Google Scholar 

  21. Das, P.: A higher order difference method for singularly perturbed parabolic partial differential equations. J. Differ. Equ. Appl. 24(3), 452–477 (2018)

    Article  MathSciNet  Google Scholar 

  22. Das, P., Vigo-Aguiar, J.: Parameter uniform optimal order numerical approximation of a class of singularly perturbed system of reaction diffusion problems involving a small perturbation parameter. J. Comput. Appl. Math. 354, 533–544 (2019)

    Article  MathSciNet  Google Scholar 

  23. Shakti, D., Mohapatra, J., Das, P., Vigo-Aguiar, J.: A moving mesh refinement based optimal accurate uniformly convergent computational method for a parabolic system of boundary layer originated reaction-diffusion problems with arbitrary small diffusion terms. J. Comput. Appl. Math. https://doi.org/10.1016/j.cam.2020.113167 (2020)

  24. Ye, X., Xu, C.: A posteriori error estimates for the fractional optimal control problems. J. Inequal. Appl. 2015(1), 141 (2015)

    Article  MathSciNet  Google Scholar 

  25. Cen, Z., Le, A., Xu, A.: A posteriori error analysis for a fractional differential equation. Int. J. Comput. Math. 94(6), 1185–1195 (2017)

  26. Kumar, K., Podila, P.C., Das, P., Ramos, H.: A graded mesh refinement approach for boundary layer originated singularly perturbed time–delayed parabolic convection diffusion problems. Math. Methods Appl. Sci. https://doi.org/10.1002/mma.7358 (2021)

  27. Das, P.: An a posteriori based convergence analysis for a nonlinear singularly perturbed system of delay differential equations on an adaptive mesh. Numer. Algorithm. 81, 465–487 (2019)

    Article  MathSciNet  Google Scholar 

  28. Diethelm, K.: The analysis of fractional differential equations: An application-oriented exposition using differential operators of caputo type. Springer Science & Business Media (2010)

  29. Podlubny, I.: Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications, vol. 198. Elsevier (1998)

  30. Szeg, G.: Orthogonal polynomials, vol. 23. American Mathematical Soc. (1939)

  31. Shen, J., Tang, T., Wang, L.L.: Spectral methods: algorithms, analysis and applications. Springer Publishing Company, Incorporated (2011)

  32. Babuška, I., Aziz, A.k.: Survey lectures on the mathematical foundations of the finite element method. Esaim-Math. Model. Num. 45(4), 1–359 (2011)

    Google Scholar 

  33. Zhao, X., Xie, Z.: Sharp error bounds for Jacobi expansions and Gegenbauer-Gauss quadrature of analytic functions. SIAM J. Numer. Anal 51(3), 1443–1469 (2013)

    Article  MathSciNet  Google Scholar 

  34. Yi, L., Guo, B.: A-posteriori error estimation for the Legendre spectral galerkin method in one-dimension. Numer. Math-Theory. Me. 3(1), 40–52 (2010)

    MathSciNet  MATH  Google Scholar 

  35. Samko, S.G., Kilbas, A.A., Marichev, O.L.: Fractional integrals and derivatives. Gordon and Breach Science Publishers, Yverdon Yverdon-les-Bains, Switzerland (1993)

Download references

Funding

This work is supported by the State Key Program of National Natural Science Foundation of China (11931003) and National Natural Science Foundation of China (41974133, 11671157).

Author information

Authors and Affiliations

  1. School of Mathematics and Information Sciences, Yantai University, Yantai, 264005, Shandong, People’s Republic of China

    Wenting Mao

  2. School of Mathematical Science, South China Normal University, Guangzhou, 520631, Guangdong, People’s Republic of China

    Yanping Chen

  3. School of Mathematics and Computational Science, Wuyi University, Jiangmen, 529020, Guangdong, People’s Republic of China

    Huasheng Wang

Authors
  1. Wenting Mao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yanping Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Huasheng Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yanping Chen.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mao, W., Chen, Y. & Wang, H. A posteriori error estimations of the Petrov-Galerkin methods for fractional Helmholtz equations. Numer Algor 89, 1095–1127 (2022). https://doi.org/10.1007/s11075-021-01147-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-021-01147-0

Keywords

Search

Navigation