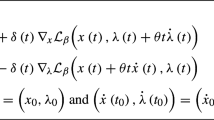Skip to main content
SpringerLink
Log in

A persistent adjoint method with dynamic time-scaling and an application to mass action kinetics

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

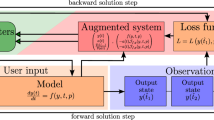
In this article, we consider an optimization problem where the objective function is evaluated at the fixed-point of a contraction mapping parameterized by a control variable, and optimization takes place over this control variable. Since the derivative of the fixed-point with respect to the parameter can usually not be evaluated exactly, an adjoint dynamical system can be used to estimate gradients. Using this estimation procedure, the optimization algorithm alternates between derivative estimation and an approximate gradient descent step. We analyze a variant of this approach involving dynamic time-scaling, where after each parameter update the adjoint system is iterated until a convergence threshold is passed. We prove that, under certain conditions, the algorithm can find approximate stationary points of the objective function. We demonstrate the approach in the settings of an inverse problem in chemical kinetics, and learning in attractor networks.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Almeida, L.B.: A learning rule for asynchronous perceptrons with feedback in a combinatorial environment. In: IEEE First International Conference on Neural Networks, San Diego, California. IEEE, New York (1987)

  2. Pineda, F.J.: Generalization of back-propagation to recurrent neural networks. Phys. Rev. Lett. 59, 2229–2232 (1987)

    Article  MathSciNet  Google Scholar 

  3. Atiya, A.F.: Learning on a general network. In: Anderson, D.Z. (ed.) Neural Information Processing Systems, pp. 22–30. American Institute of Physics (1988)

  4. Pineda, F.J.: Dynamics and architecture for neural computation. J. Complex. 4(3), 216–245 (1988)

    Article  MathSciNet  Google Scholar 

  5. Pineda, F.J.: Recurrent backpropagation and the dynamical approach to adaptive neural computation. Neural Comput. 1(2), 161–172 (1989)

    Article  Google Scholar 

  6. Riaza, R., Zufiria, P.J.: Differential-algebraic equations and singular perturbation methods in recurrent neural learning. Dynamical Systems: An International Journal 18(1), 89–105 (2003)

    Article  MathSciNet  Google Scholar 

  7. Chris Tseng, H., Šiljak, D.D.: A learning scheme for dynamic neural networks: Equilibrium manifold and connective stability. Neural Netw. 8(6), 853–864 (1995)

    Article  Google Scholar 

  8. Lohmiller, W., Slotine, J.-J.E.: On contraction analysis for non-linear systems. Automatica 34(6), 683–696 (1998)

    Article  MathSciNet  Google Scholar 

  9. Flynn, T.: Timescale separation in recurrent neural networks. Neural Comput. 27(6), 1321–1344 (2015)

    Article  MathSciNet  Google Scholar 

  10. Younes, L.: On the convergence of markovian stochastic algorithms with rapidly decreasing ergodicity rates. Stochastics: An International Journal of Probability and Stochastic Processes 65(3-4), 177–228 (1999)

    MathSciNet  MATH  Google Scholar 

  11. Tieleman, T.: Training restricted boltzmann machines using approximations to the likelihood gradient. In: Proceedings of the 25th International Conference on Machine Learning, pp. 1064–1071. ACM (2008)

  12. Hornik, K., Kuan, C.-M.: Gradient-based learning in recurrent networks. Neural Netw. World 4, 157–172 (1994)

    Google Scholar 

  13. Giles, M.B., Pierce, N.A.: An introduction to the adjoint approach to design. Flow Turbul. Combust. 65(3-4), 393–415 (2000)

    Article  Google Scholar 

  14. Peter, J.E.V., Dwight, R.P.: Numerical sensitivity analysis for aerodynamic optimization: a survey of approaches. Comput. Fluids 39(3), 373–391 (2010)

    Article  MathSciNet  Google Scholar 

  15. Giles, M.: On the iterative solution of adjoint equations. In: Corliss, G., Faure, C., Griewank, A., Hascoët, L., Naumann, U. (eds.) Automatic Differentiation of Algorithms, pp 145–151. New York, Springer (2002)

  16. Ta’asan, S.: One shot methods for optimal control of distributed parameter systems i: Finite dimensional control. Technical report, Institute for Computer Applications in Science and Engineering (ICASE), Hampton VA (1991)

  17. Hazra, S.B., Jameson, A.: One-shot pseudo-time method for aerodynamic shape optimization using the navier–stokes equations. Int. J. Numer. Methods Fluids 68(5), 564–581 (2012)

    Article  MathSciNet  Google Scholar 

  18. Günther, S., Gauger, N.R., Wang, Q.: Simultaneous single-step one-shot optimization with unsteady {PDEs}. J. Comput. Appl. Math. 294, 12–22 (2016)

    Article  MathSciNet  Google Scholar 

  19. Jaworski, A., Cusdin, P., Muller, J.-D.: Uniformly converging simultaneous time-stepping methods for optimal design. In: Schilling, R., Haase, W., Periaux, J., Baier, H., Bugeda, G. (eds.) Evolutionary and Deterministic Methods for Design, Optimization and Control with Applications to Industrial and Societal Problems (EUROGEN) (2005)

  20. Hamdi, A., Griewank, A.: Reduced quasi-newton method for simultaneous design and optimization. Comput. Optim. Appl. 49(3), 521–548 (2011)

    Article  MathSciNet  Google Scholar 

  21. Flynn, T.: Convergence of one-step adjoint methods. In: Proceedings of the 22nd International Symposium on Mathematical Theory of Networks and Systems (2016)

  22. Bertsekas, D.P., Tsitsiklis, J.N.: Gradient convergence in gradient methods with errors. SIAM J. Optim. 10(3), 627–642 (2000)

    Article  MathSciNet  Google Scholar 

  23. Nesterov, Y.: Introductory lectures on convex optimization: a basic course, vol. 87. Springer Science & Business Media (2013)

  24. Baldi, P.: Gradient descent learning algorithm overview: a general dynamical systems perspective. IEEE Trans. Neural Netw. 6(1), 182–195 (1995)

    Article  Google Scholar 

  25. Russo, G., Di Bernardo, M., Sontag, E.D.: Global entrainment of transcriptional systems to periodic inputs, vol. 6 (2010)

  26. Sontag, E.D.: Contractive systems with inputs. In: Perspectives in Mathematical System Theory, Control, and Signal Processing, pp. 217–228. Springer (2010)

  27. Gnacadja, G.: Fixed points of order-reversing maps in \(\mathbb {R}_{n > 0}\) and chemical equilibrium. Math. Methods Appl. Sci. 30(2), 201–211 (2007)

    Article  MathSciNet  Google Scholar 

  28. van Dorp, M. G. A., Berger, F., Carlon, E.: Computing equilibrium concentrations for large heterodimerization networks. Phys. Rev. E 84, 036114 (2011)

    Article  Google Scholar 

  29. Anderson, D.F., Kurtz, T.G.: Stochastic Analysis of Biochemical Systems. Springer, Berlin (2015)

    Book  Google Scholar 

  30. Horn, R.A., Johnson, C.R. (eds.): Matrix Analysis. Cambridge University Press, New York (1986)

Download references

Funding

This research was supported, in part, under the National Science Foundation Grants CNS-0958379, CNS-0855217, and ACI-1126113; the City University of New York High Performance Computing Center at the College of Staten Island; the United State Department of Energy contract DE-SC0012704; and DOE Office of Science under grant ASCR KJ040201.

Author information

Authors and Affiliations

  1. Computational Science Initiative, Brookhaven National Laboratory, Upton, NY, 11973, USA

    Thomas Flynn

Authors
  1. Thomas Flynn
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Thomas Flynn.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Flynn, T. A persistent adjoint method with dynamic time-scaling and an application to mass action kinetics. Numer Algor 89, 87–113 (2022). https://doi.org/10.1007/s11075-021-01107-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-021-01107-8

Keywords

Search

Navigation