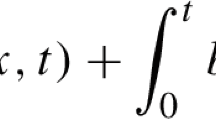Abstract
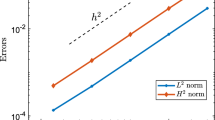
An initial-boundary value problem of the form \({D}_{t}^{\alpha } u+{\varDelta }^{2}u-c{\varDelta } u =f\) is considered, where \({D}_{t}^{\alpha }\) is a Caputo temporal derivative of order α ∈ (0,1) and c is a nonnegative constant. The spatial domain \({\varOmega } \subset \mathbb {R}^{d}\) for some d ∈{1,2,3}, with Ω bounded and convex. The boundary conditions are u = Δu = 0 on ∂Ω. A priori bounds on the solution are established, given sufficient regularity and compatibility of the data; typical solutions have a weak singularity at the initial time t = 0. The problem is rewritten as a system of two second-order differential equations, then discretised using standard finite elements in space together with the L1 discretisation of \({D}_{t}^{\alpha }\) on a graded temporal mesh. The numerical method computes approximations \({u_{h}^{n}}\) and \({{p}_{h}^{n}}\) of u(⋅,tn) and Δu(⋅,tn) at each time level tn. The stability of the method (i.e. a priori bounds on \(\|{{u}_{h}^{n}}\|_{L^{2}({\varOmega })}\) and \(\|{p_{h}^{n}}\|_{L^{2}({\varOmega })}\)) is established by means of a new discrete Gronwall inequality that is α-robust, i.e. remains valid as α → 1−. Error bounds on \(\|u(\cdot , t_{n}) - {u_{h}^{n}}\|_{L^{2}({\varOmega })}\) and \(\|{\varDelta } u(\cdot , t_{n}) - {{p}_{h}^{n}}\|_{L^{2}({\varOmega })}\) are then derived; these bounds are of optimal order in the spatial and temporal mesh parameters for each fixed value of α, and they are α-robust if one considers α → 1−.
Similar content being viewed by others
References
Alikhanov, A.A.: Boundary value problems for the diffusion equation of the variable order in differential and difference settings. Appl. Math. Comput. 219 (8), 3938–3946 (2012)
An, Y., Liu, R.: Existence of nontrivial solutions of an asymptotically linear fourth-order elliptic equation. Nonlinear Anal. 68(11), 3325–3331 (2008)
Chen, H., Stynes, M.: Blow-up of error estimates in time-fractional initial-boundary value problems. IMA J. Numer Anal. (To appear) (2020)
Diethelm, K.: The Analysis of Fractional Differential Equations volume 2004 of Lecture Notes in Mathematics. Springer, Berlin (2010). An application-oriented exposition using differential operators of Caputo type
Evans, L.C.: Partial Differential Equations, volume 19 of Graduate Studies in Mathematics. American Mathematical Society, Providence (1998)
Ganesan, S., Tobiska, L.: Finite Elements. Theory and Algorithms. Cambridge University Press, Delhi (2017)
Huang, C., Stynes, M.: Superconvergence of the direct discontinuous Galerkin method for a time-fractional initial-boundary value problem. Numer. Methods Partial Differ. Equ. 35(6), 2076–2090 (2019)
Huang, C., Stynes, M.: Optimal spatial H1-norm analysis of a finite element method for a time-fractional diffusion equation. J. Comput. Appl. Math. 367, 112435 (2020)
Huang, C., Stynes, M.: Superconvergence of a finite element method for the multi-term time-fractional diffusion problem. J. Sci. Comput. 82(1), Paper No. 10, 17 (2020)
Kopteva, N.: Error analysis of the L1 method on graded and uniform meshes for a fractional-derivative problem in two and three dimensions. Math. Comput. 88(319), 2135–2155 (2019)
Lazer, A.C., McKenna, P.J.: Large-amplitude periodic oscillations in suspension bridges: some new connections with nonlinear analysis. SIAM Rev. 32(4), 537–578 (1990)
Li, J.: Optimal error estimates of mixed finite element methods for a fourth-order nonlinear elliptic problem. J. Math. Anal. Appl. 334(1), 183–195 (2007)
Podlubny, I.: Fractional Differential Equations, volume 198 of Mathematics in Science and Engineering. Academic Press, Inc., San Diego (1999). An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications
Quarteroni, A., Valli, A.: Numerical Approximation of Partial Differential Equations volume 23 of Springer Series in Computational Mathematics. Springer, Berlin (1994)
Sakamoto, K., Yamamoto, M.: Initial value/boundary value problems for fractional diffusion-wave equations and applications to some inverse problems. J. Math. Anal. Appl. 382(1), 426–447 (2011)
Stynes, M., O’Riordan, E., Gracia, J.L.: Error analysis of a finite difference method on graded meshes for a time-fractional diffusion equation. SIAM J. Numer. Anal. 55(2), 1057–1079 (2017)
Thomée, V.: Galerkin Finite Element Methods for Parabolic Problems, 2Nd Revised and Expanded ed. Springer, Berlin (2006). 2nd revised and expanded ed. edition
Zhong, J., Liao, H.-L., Ji, B., Zhang, L.: A fourth-order compact solver for fractional-in-time fourth-order diffusion equations. Preprint, Beijing CSRC (2019)
Funding
The research of Martin Stynes is supported in part by the National Natural Science Foundation of China under grant NSAF-U1930402. The research of Chaobao Huang is supported in part by the National Natural Science Foundation of China under grants 11801332 and 11971276.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Huang, C., Stynes, M. α-robust error analysis of a mixed finite element method for a time-fractional biharmonic equation. Numer Algor 87, 1749–1766 (2021). https://doi.org/10.1007/s11075-020-01036-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11075-020-01036-y
Keywords
- Time-fractional problem
- Weak singularity
- Mixed finite element method
- Discrete Gronwall inequality
- α-robust