Skip to main content
SpringerLink
Log in

Nonlinear mode coupling in a passively isolated mechanical system

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

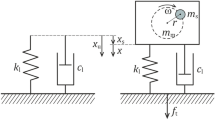
Recent studies in passively isolated systems have shown that mode coupling is desirable for better vibration suppression, thus refuting the long-standing rule of modal decoupling. However, these studies have ignored the nonlinearities in the isolators. In this work, we consider stiffness nonlinearity from pneumatic isolators and study the nonlinear forced damped vibrations of a passively isolated ultra-precision manufacturing (UPM) machine. Experimental analysis is conducted to guide the mathematical formulation. The system comprises linearly and nonlinearly coupled in-plane horizontal and rotational motion of the UPM machine with quadratic nonlinear stiffness from the isolators. We present an analytical study using the method of multiple scales and the method of harmonic balance for different cases of external resonances, viz., the primary and the secondary resonances (superharmonic and combined resonances) with 1 : 2 internal resonance between the modes. We further validate our analytical findings using direct numerical integration and observe an excellent match. On extending our analysis, we observe the existence of subcritical, supercritical, and s-shaped bifurcation depending on the location of the isolators and the case of external resonance. Also, the saturation and quasi-saturation phenomenon are observed for the case of resonances close to the higher natural frequency and combined resonance, respectively. A parametric study is conducted to examine the effect of different parameters on the dynamics of the system, and consecutively the critical parameters of the system are identified for different cases of external resonance.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28
Fig. 29
Fig. 30
Fig. 31
Fig. 32

Similar content being viewed by others

References

  1. Alting, L., Kimura, F., Hansen, H.N., Bissacco, G.: Micro engineering. CIRP Ann.-Manuf. Technol. 52(2), 635–657 (2003)

    Article  Google Scholar 

  2. Hansen, H.N., Carneiro, K., Haitjema, H., De Chiffre, L.: Dimensional micro and nano metrology. CIRP Ann. 55(2), 721–743 (2006)

    Article  Google Scholar 

  3. Ehmann, K.F.: A Synopsis of us Micro-Manufacturing Research and Development Activities and Trends, pp. 7–13. Borovets, Bulgaria (2007)

    Google Scholar 

  4. Karnopp, D.: Active and semi-active vibration isolation. In: Elarabi, M.E., Wifi, A.S., Wifi, A.S. (eds.) Current Advances in Mechanical Design and Production VI, pp. 409–423. Elsevier (1995)

  5. Schellekens, P., Rosielle, N., Vermeulen, H., Vermeulen, M.M.P.A., Wetzels, S.F.C.L., Pril, W.: Design for precision: current status and trends. CIRP Ann. 47(2), 557–586 (1998)

    Article  Google Scholar 

  6. Liu, Y., Waters, T.P., Brennan, M.J.: A comparison of semi-active damping control strategies for vibration isolation of harmonic disturbances. J. Sound Vib. 280(1–2), 21–39 (2005)

    Article  MathSciNet  Google Scholar 

  7. Fuller, C.C., Elliott, S., Nelson, P.A.: Active Control of Vibration. Academic Press, USA (1996)

    Book  Google Scholar 

  8. Shiba, K., Mase, S., Yabe, Y., Tamura, K.: Active/passive vibration control systems for tall buildings. Smart Mater. Struct. 7(5), 588 (1998)

    Article  Google Scholar 

  9. Jalili, N.: A comparative study and analysis of semi-active vibration-control systems. J. Vib. Acoust. 124(4), 593–605 (2002)

    Article  MathSciNet  Google Scholar 

  10. DeBra, D.B.: Vibration isolation of precision machine tools and instruments. CIRP Ann.-Manuf. Technol. 41(2), 711–718 (1992)

    Article  Google Scholar 

  11. Rivin, E.I.: Vibration isolation of precision equipment. Precis. Eng. 17(1), 41–56 (1995)

    Article  Google Scholar 

  12. Franchek, M.A., Ryan, M.W., Bernhard, R.J.: Adaptive passive vibration control. J. Sound Vib. 189(5), 565–585 (1996)

    Article  Google Scholar 

  13. Weaver Jr., W., Timoshenko, S.P., Young, D.H.: Vibration Problems in Engineering. Wiley, New York (1990)

    Google Scholar 

  14. Harris, C.M., Piersol, A.G.: Harris’ Shock and Vibration Handbook, vol. 5. McGraw-Hill, New York (2002)

    Google Scholar 

  15. Rivin, E.I.: Passive Vibration Isolation. American Society of Mechanical, (2003)

  16. Crede, C.E.: Vibration and Shock Isolation. Wiley, New York (1951)

    Google Scholar 

  17. Snowdon, J.C.: Vibration and Shock in Damped Mechanical Systems. Wiley, New York (1968)

    Google Scholar 

  18. Snowdon, J.C.: Vibration isolation: use and characterization. J. Acoust. Soc. Am. 66(5), 1245–1274 (1979)

    Article  Google Scholar 

  19. Ryaboy, V.M.: Static and dynamic stability of pneumatic vibration isolators and systems of isolators. J. Sound Vib. 333(1), 31–51 (2014)

    Article  Google Scholar 

  20. Subrahmanyan, P.K., Trumper, D.L.: Synthesis of passive vibration isolation mounts for machine tools-a control systems paradigm. In: American Control Conference, 2000. Proceedings of the 2000, vol. 4, pp. 2886–2891. IEEE (2000)

  21. Rivin, E.I.: Vibration isolation of precision objects. Sound Vib. 40(7), 12–20 (2006)

    Google Scholar 

  22. Okwudire, C.E.: A study on the effects of isolator, motor and work surface heights on the vibrations of ultra-precision machine tools, In: Proceeding of ICOMM, Evanston, Illinois, pp. 31–36, March (2012)

  23. Shin, Y.-H., Kim, K.-J., Chang, P.-H., Han, D.K.: Three degrees of freedom active control of pneumatic vibration isolation table by pneumatic and time delay control technique. J. Vib. Acoust. 132(5), 051013 (2010)

    Article  Google Scholar 

  24. Vermeulen, M.M.P.A., Rosielle, P.C.J.N., Schellekens, P.H.J.: Design of a high-precision 3d-coordinate measuring machine. CIRP Ann.-Manuf. Technol. 47(1), 447–450 (1998)

    Article  Google Scholar 

  25. Kato, T., Kawashima, K., Sawamoto, K., Kagawa, T.: Active control of a pneumatic isolation table using model following control and a pressure differentiator. Precis. Eng. 31(3), 269–275 (2007)

    Article  Google Scholar 

  26. Erin, C., Wilson, B., Zapfe, J.: An improved model of a pneumatic vibration isolator: theory and experiment. J. Sound Vib. 218(1), 81–101 (1998)

    Article  Google Scholar 

  27. Bukhari, M., Barry, O: On the nonlinear vibration analysis of ultra precision manufacturing machines with mode coupling. In: ASME 2017 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference (2017)

  28. Kirk, C.L.: Non-linear random vibration isolators. J. Sound Vib. 124(1), 157–182 (1988)

    Article  Google Scholar 

  29. Ruzicka, J.E., Derby, T.F.: Influence of damping in vibration isolation. Technical Report (1971)

  30. Ibrahim, R.A.: Recent advances in nonlinear passive vibration isolators. J. Sound Vib. 314(3–5), 371–452 (2008)

    Article  Google Scholar 

  31. Ewins, D.J., Rao, S.S., Braun, S.G.: Encyclopedia of Vibration, Three-Volume Set. Academic Press, USA (2002)

    Google Scholar 

  32. Racca Sr, R: How to select power-train isolators for good performance and long service life. SAE Transactions, pp. 3439–3450 (1982)

  33. Andrews, F.: Items which can compromise vibration isolation (2012)

  34. Okwudire, C.E., Lee, J.: Minimization of the residual vibrations of ultra-precision manufacturing machines via optimal placement of vibration isolators. Precis. Eng. 37(2), 425–432 (2013)

    Article  Google Scholar 

  35. Lee, J., Okwudire, C.E.: Reduction of vibrations of passively-isolated ultra-precision manufacturing machines using mode coupling. Precis. Eng. 43, 164–177 (2016)

    Article  Google Scholar 

  36. Natsiavas, S., Tratskas, P.: On vibration isolation of mechanical systems with non-linear foundations. J. Sound Vib. 194(2), 173–185 (1996)

    Article  Google Scholar 

  37. Nayfeh, A.H., Mook, D.T., Marshall, L.R.: Nonlinear coupling of pitch and roll modes in ship motions. J. Hydronaut. 7(4), 145–152 (1973)

    Article  Google Scholar 

  38. Karabalin, R.B., Cross, M.C., Roukes, M.L.: Nonlinear dynamics and chaos in two coupled nanomechanical resonators. Phys. Rev. B 79(16), 165309 (2009)

    Article  Google Scholar 

  39. Mathis, A.T., Quinn, D.D.: Transient dynamics, damping, and mode coupling of nonlinear systems with internal resonances. Nonlinear Dyn. 99(1), 269–281 (2020)

    Article  Google Scholar 

  40. Rocha, R.T., Balthazar, J.M., Quinn, D.D., Tusset, A.M., Felix, J.L.P.: Non-ideal system with quadratic nonlinearities containing a two-to-one internal resonance. In: ASME 2016 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. American Society of Mechanical Engineers Digital Collection (2016)

  41. Krifa, M., Bouhaddi, N., Chevallier, G., Cogan, S., Kacem, N.: Estimation and correction of the modal damping error involving linear and nonlinear localized dissipation. Eur. J. Mech.-A/Solids 66, 296–308 (2017)

    Article  MathSciNet  Google Scholar 

  42. Heertjes, M., van de Wouw, N.: Nonlinear dynamics and control of a pneumatic vibration isolator. J. Vib. Acoust. 128(4), 439–448 (2006)

    Article  Google Scholar 

  43. Nayfeh, A.H., Mook, D.T.: Nonlinear Oscillations. Wiley, New York (2008)

    MATH  Google Scholar 

  44. Balachandran, B., Nayfeh, A.H.: Cyclic motions near a hopf bifurcation of a four-dimensional system. Nonlinear Dyn. 3(1), 19–39 (1992)

    Article  Google Scholar 

  45. Poole, E., Roberson, B., Stephenson, B.: Weak allee effect, grazing, and s-shaped bifurcation curves. Invol. J. Math. 5(2), 133–158 (2013)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This work is funded by National Science Foundation (NSF) Award CMMI #2000984: Nonlinear Dynamics of Pneumatic Isolators in Ultra-Precising Manufacturing Machine.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Virginia Tech, Blacksburg, VA, 24061, USA

    Sunit K. Gupta, Mohammad A. Bukhari & Oumar R. Barry

Authors
  1. Sunit K. Gupta
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mohammad A. Bukhari
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Oumar R. Barry
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Oumar R. Barry.

Ethics declarations

Conflict of Interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A: primary resonance near \(\omega _1\)

$$\begin{aligned}&D_{0,0}{\eta }_1+\beta ^2(\eta _1-\alpha \vartheta _1)\nonumber \\&\quad =-2i\left( {D_1 A_1}{\varLambda _1}+{A_1}\zeta \beta {\varLambda _1}-{A_1}\zeta \,\beta \,\alpha \right) {\omega _1}e^{i\omega _1T_0}\nonumber \\&\qquad -2i \left( D_1A_2{\varLambda _2}+{A_2}\zeta \beta \,{ \varLambda _2}\nonumber \right. \\&\left. \quad -{A_2} \zeta \beta \alpha \right) {\omega _2}e^{i\omega _2T_0}\nonumber \\&\qquad - {A_1}^{2}{\alpha _1}{ m_r}\left( \alpha -{\varLambda _1} \right) ^{2}e^{2i\omega _1T_0}\nonumber \\&\qquad -{A_2}^{2}{\alpha _1}{ m_r}\left( \alpha -{\varLambda _2} \right) ^{2}e^{2i\omega _2T_0}\nonumber \\&\qquad -2{A_1} {{\bar{A}}_2}{ \alpha _1}{m_r}\left( \alpha - {\varLambda _1} \right) \left( \alpha -{{\bar{\varLambda }}_2}\right) e^{i\left( \omega _1-\omega _2\right) T_0}\nonumber \\&\qquad +2\,{A_1} {A_2}{ \alpha _1}{m_r}\left( \alpha - {\varLambda _1} \right) \left( \alpha -{\varLambda _2} \right) e^{i\left( \omega _1+\omega _2\right) T_0}\nonumber \\&\qquad +2\,{A_1}{{\bar{A}}_1}{ \alpha _1}{m_r} \left( \alpha -{\varLambda }_1 \right) \left( \alpha -{{\bar{\varLambda }}_1} \right) \nonumber \\&\qquad +2{A_2}{{\bar{A}}_4}{ \alpha _1}{m_r}\left( \alpha -{\varLambda _2} \right) \left( \alpha -{{\bar{\varLambda }}_2} \right) \nonumber \\&\qquad +\frac{f_0}{2}m_re^{i\left( \omega _1T_0+\sigma _1T_1\right) }+ C.C.\,, \end{aligned}$$
(56a)
$$\begin{aligned}&D_{0,0}\vartheta _1+{\vartheta }_{{1}}-{k_r}\alpha \left( \eta _1-\alpha \vartheta _1\right) \nonumber \\&\quad =-2i\omega _1\left( D_1{A_1}+{\sqrt{\frac{k_r}{m_r}}} {\zeta {\alpha }^{2}{A_1}}\nonumber \right. \\&\left. \qquad +\kappa {A_1} -{\sqrt{\frac{k_r}{m_r}}} {\zeta {\alpha }{A_1}\varLambda _1}\right) e^{i\omega _1T_0}\nonumber \\&\qquad -2i\omega _2\left( D_1{A_2} +{\sqrt{\frac{k_r}{m_r}}} {\zeta {\alpha }^{2}{A_2}}\nonumber \right. \\&\qquad \left. +\kappa {A_2} -{\sqrt{\frac{k_r}{m_r}}} {\zeta {\alpha }{A_2}\varLambda _2}\right) e^{i\omega _2T_0}\nonumber \\&\qquad +{A_1}^{2} \left( \alpha _1\alpha (\alpha -\varLambda _1)^2-q_{zr} \right) e^{2i\omega _1T_0}\nonumber \\&\qquad +{A_2}^{2} \left( \alpha _1\alpha (\alpha -\varLambda _2)^2-q_{zr} \right) e^{2i\omega _2T_0}\nonumber \\&\qquad +2{A_1}{{\bar{A}}_2}\left( \alpha _1\alpha (\alpha -\varLambda _1)(\alpha -{\bar{\varLambda }}_2) -{q_{zr}} \right) e^{i\left( \omega _1-\omega _2\right) T_0}\nonumber \\&\qquad +2{A_1}{A_2}\left( \alpha _1\alpha (\alpha -\varLambda _1)(\alpha -{\varLambda }_2) -{q_{zr}} \right) e^{i(\omega _1+\omega _2)T_0}\nonumber \\&\qquad +2\,{A_1}{{\bar{A}}_1} \left( \alpha _1\alpha (\alpha -\varLambda _1)(\alpha -{\bar{\varLambda }}_1)-q_{zr} \right) \nonumber \\&\qquad +2\,{A_2}{{\bar{A}}_2}\nonumber \\&\qquad \left( \alpha _1\alpha (\alpha -\varLambda _2)(\alpha -{\bar{\varLambda }}_2)-q_{zr} \right) \nonumber \\&\qquad +\frac{f_0}{2}\alpha e^{i(\omega _1T_0+\sigma _1T_1)}+C.C.\,, \varGamma _1\nonumber \\&\quad =\frac{4\omega _1\zeta \left( l_1\beta -\alpha \sqrt{\frac{k_r}{m_r}} \right) (\alpha -\varLambda _1)-4\kappa \omega _1}{4\omega _1(1+l_1\varLambda _1)}\nonumber \\&\varGamma _2=\frac{\alpha _1\left( \alpha -l_1m_r\right) (\alpha -\varLambda _2)^2-q_{zr}}{4\omega _1(1+l_1\varLambda _1)}\nonumber \\&\varGamma _3=\frac{2(l_1m_r-\alpha )}{4\omega _1(1+l_1\varLambda _1)}\nonumber \\&\varGamma _4=\frac{\alpha _1(l_2m_r-\alpha )(\alpha -{\bar{\varLambda }}_2)(\alpha -\varLambda _1)+q_{zr} }{2\omega _2(1+l_2\varLambda _2)}\nonumber \\&\varGamma _5=\frac{2\zeta \omega _2\left( l_2\beta -\alpha \sqrt{\frac{k_r}{m_r}}\right) (\alpha -\varLambda _2)-2\kappa \omega _2}{4\omega _2(1+l_2\varLambda _2)} \end{aligned}$$
(56b)

Appendix B: primary resonance near \(\omega _2\)

$$\begin{aligned}&{\mathcal {O}}(\epsilon ^0)\quad : D_{0,0}{\eta }_{{0}} +{\beta }^{2}\left( {\eta }_{{0}} -\alpha \,{\vartheta }_{{0}}\right) =0\,, \end{aligned}$$
(57a)
$$\begin{aligned}&D_{0,0}{\vartheta }_{{0}} +{\vartheta }_{{0}} -{k_r}\,\alpha \left( {\eta }_{{0}} -{\alpha }{\vartheta }_{{0}} \right) =0 \end{aligned}$$
(57b)
$$\begin{aligned}&{\mathcal {O}}(\epsilon )\quad : D_{0,0}{\eta }_1+\beta ^2(\eta _1-\alpha \vartheta _1)\nonumber \\&\quad =-2\zeta \beta \left( D_0\eta _0-\alpha D_0\vartheta _0\right) \nonumber \\&\qquad -\alpha _1 m_r\left( \eta _0-\alpha \vartheta _0\right) ^2- 2D_{0,1}\eta _0\nonumber \\&\qquad +f_0 m_r \cos (\omega _2T_0+\sigma _1T_1) \end{aligned}$$
(58a)
$$\begin{aligned}&D_{0,0}\vartheta _1+{\vartheta }_{{1}}-{k_r}\alpha \left( \eta _1-\alpha \vartheta _1\right) \nonumber \\&\quad =2\zeta \sqrt{\frac{k_r}{m_r}}\alpha \left( D_0\eta _0-\alpha D_0\vartheta _0\right) -2D_{0,1}\vartheta _0\nonumber \\&\qquad +{\alpha _1}{\alpha }(\eta _0-\alpha \vartheta _0)^{2}-{q_{zr}}{\vartheta }_{{0}}^{2}\nonumber \\&\qquad -2\kappa D_0\vartheta _0-{f_0}\alpha \cos \left( {\omega _2}\,T_{{0}} +\sigma _1T_1\right) \,. \end{aligned}$$
(58b)

Appendix C: secondary resonance

$$\begin{aligned}&D_{0,0}{\eta }_1+\beta ^2(\eta _1-\alpha \vartheta _1)\nonumber \\&\quad =-2i\left( {D_1 A_1}{\varLambda _1}+{A_1}\zeta \beta {\varLambda _1}-{A_1}\zeta \,\beta \,\alpha \right) {\omega _1}e^{i\omega _1T_0}\nonumber \\&\qquad -2i \left( D_1A_2{\varLambda _2}+{A_2}\zeta \beta \,{ \varLambda _2}-{A_2} \zeta \beta \alpha \right) {\omega _2}e^{i\omega _2T_0}\nonumber \\&\qquad - {A_1}^{2}{\alpha _1}{ m_r}\left( \alpha -{\varLambda _1} \right) ^{2}e^{2i\omega _1T_0}-{A_2}^{2}{\alpha _1}{ m_r}\nonumber \\&\qquad \left( \alpha -{\varLambda _2} \right) ^{2}e^{2i\omega _2T_0}\nonumber \\&\qquad -2{A_1} {{\bar{A}}_2}{ \alpha _1}{m_r}\left( \alpha - {\varLambda _1} \right) \left( \alpha -{{\bar{\varLambda }}_2}\right) e^{i\left( \omega _1-\omega _2\right) T_0}\nonumber \\&\qquad +2\,{A_1} {A_2}{ \alpha _1}{m_r}\left( \alpha - {\varLambda _1} \right) \left( \alpha -{\varLambda _2} \right) e^{i\left( \omega _1+\omega _2\right) T_0}\nonumber \\&\qquad +{A_1}{\alpha _1}{m_r}{f_0} \left( \alpha -{\varLambda _1}\right) \left( {\varPhi _1}-\alpha {\varPhi _2} \right) e^{i\left( \omega _1-\omega _r\right) T_0}\nonumber \\&\qquad +{A_1} {\alpha _1}{m_r}{f_0} \left( \alpha -{\varLambda _1} \right) \left( {\varPhi _1}-\alpha {\varPhi _2} \right) e^{i\left( \omega _1+\omega _r\right) T_0}\nonumber \\&\qquad +{A_2}{\alpha _1}{m_r}{f_0} \left( \alpha -{\varLambda _2} \right) \left( {\varPhi _1}-\alpha {\varPhi _2} \right) e^{i\left( \omega _2-\omega _r\right) T_0}\nonumber \\&\qquad +{A_2} {\alpha _1}{m_r}{f_0} \left( \alpha -{\varLambda _2} \right) \left( {\varPhi _1}-\alpha {\varPhi _2} \right) e^{i\left( \omega _2+\omega _r\right) T_0}\nonumber \\&\qquad -\frac{1}{4}f^2_0\alpha _1m_r(\varPhi _1-\alpha \varPhi _2)^2e^{2i\omega _r T_0}\nonumber \\&\qquad -i \left( \varPhi _1-{\varPhi _2}\,\alpha \right) \beta {f_0}{ \omega _r}\,\zeta e^{i\omega _r T_0}\nonumber \\&\qquad +C.C.+CVF_1 \end{aligned}$$
(59)
$$\begin{aligned}&D_{0,0}\vartheta _1+{\vartheta }_{{1}}-{k_r}\alpha \left( \eta _1-\alpha \vartheta _1\right) \nonumber \\&\quad =-2i\omega _1\left( D_1{A_1}+{\sqrt{\frac{k_r}{m_r}}} {\zeta {\alpha }^{2}{A_1}}\nonumber \right. \\&\qquad \left. +\kappa {A_1} -{\sqrt{\frac{k_r}{m_r}}} {\zeta {\alpha }{A_1}\varLambda _1}\right) e^{i\omega _1T_0}\nonumber \\&\qquad -2i\omega _2\left( D_1{A_2} +{\sqrt{\frac{k_r}{m_r}}} {\zeta {\alpha }^{2}{A_2}}\nonumber \right. \\&\qquad \left. +\kappa {A_2} -{\sqrt{\frac{k_r}{m_r}}} {\zeta {\alpha }{A_2}\varLambda _2}\right) e^{i\omega _2T_0}\nonumber \\&\qquad +{A_1}^{2} \left( \alpha _1\alpha (\alpha -\varLambda _1)^2-q_{zr} \right) e^{2i\omega _1T_0}\nonumber \\&\qquad +{A_2}^{2} \left( \alpha _1\alpha (\alpha -\varLambda _2)^2-q_{zr} \right) \nonumber \\&\qquad e^{2i\omega _2T_0}\nonumber \\&\qquad +2{A_1}{{\bar{A}}_2}\left( \alpha _1\alpha (\alpha -\varLambda _1)(\alpha -{\bar{\varLambda }}_2) -{q_{zr}} \right) \nonumber \\&\qquad e^{i\left( \omega _1-\omega _2\right) T_0}\nonumber \\&\qquad +2{A_1}{A_2}\left( \alpha _1\alpha (\alpha -\varLambda _1)(\alpha -{\varLambda }_2) -{q_{zr}} \right) \nonumber \\&\qquad e^{i(\omega _1+\omega _2)T_0}\nonumber \\&\qquad -A_1f_0\left( {\alpha _1}\alpha \left( \alpha -{\varLambda _1} \right) \left( \varPhi _1-{ \varPhi _2}\,\alpha \right) +\varPhi _2q_{zr}\right) \nonumber \\&\qquad e^{i(\omega _1-\omega _r)T_0}\nonumber \\&\qquad -A_1f_0\left( {\alpha _1}\alpha \left( \alpha -{\varLambda _1} \right) \left( \varPhi _1-{ \varPhi _2}\,\alpha \right) +\varPhi _2q_{zr}\right) \nonumber \\&\qquad e^{i(\omega _1+\omega _r)T_0}\nonumber \\&\qquad -A_2f_0\left( {\alpha _1}\alpha \left( \alpha -{\varLambda _2} \right) \left( \varPhi _1-{ \varPhi _2}\,\alpha \right) +\varPhi _2q_{zr}\right) \nonumber \\&\qquad e^{i(\omega _2-\omega _r)T_0}\nonumber \\&\qquad -A_2f_0\left( {\alpha _1}\alpha \left( \alpha -{\varLambda _2} \right) \left( \varPhi _1-{ \varPhi _2}\,\alpha \right) +\varPhi _2q_{zr}\right) \nonumber \\&\qquad e^{i(\omega _2+\omega _r)T_0}\nonumber \\&\qquad +\frac{1}{4}f^2_0\left( \alpha _1\alpha (\varPhi _1-\alpha \varPhi _2)^2-q_{zr}\varPhi ^2_2\right) e^{2i\omega _rT_0} \nonumber \\&\qquad +i \left( -{\varPhi _2}\kappa -{\varPhi _2}{\alpha }^{2}{\zeta }{\sqrt{\frac{k_r}{m_r}}}\nonumber \right. \\&\left. \qquad + \alpha {\zeta }{\sqrt{\frac{k_r}{m_r}}}{\varPhi _1} \right) {f_0}\,{\omega _r}e^{i\omega _rT_0}+C.C.+CVF_2 \end{aligned}$$
(60)

Appendix D: superharmonic resonance near \(\omega _1\)

$$\begin{aligned} \varGamma _1&=\frac{4\zeta l_1\beta \omega _1(\alpha -\varLambda _1)-4\alpha \sqrt{\frac{k_r}{m_r}}\zeta \omega _1 (\alpha -\varLambda _1)-4\kappa \omega _1}{4\omega _1(1+l_1\varLambda _1)}\,,\nonumber \\ \varGamma _2&=\frac{-\alpha _1(\alpha -\varLambda _2)^2(l_1m_r-\alpha )-q_{zr}}{4\omega _1(1+l_1\varLambda _1)}\,,\nonumber \\ \varGamma _3&=\frac{-\alpha _1(\varPhi _1-\alpha \varPhi _2)^2(l_1m_r-\alpha )-q_{zr}\varPhi ^2_2}{4\omega _1(1+l_1\varLambda _1)}\,,\nonumber \\ \varGamma _4&=\frac{\alpha _1(\alpha -{\bar{\varLambda }}_2)(\alpha -\varLambda _1)(l_2m_r-\alpha )+q_{zr}}{2\omega _2(1+l_2\varLambda _2)}\,,\nonumber \\ \varGamma _5&=\frac{2\zeta l_2\beta \omega _2(\alpha -\varLambda _2)-2\alpha \sqrt{\frac{k_r}{m_r}}\zeta \omega _2 (\alpha -\varLambda _2)-2\kappa \omega _2}{2\omega _1(1+l_2\varLambda _2)}\,. \end{aligned}$$
(61)

Appendix E: combined resonance

$$\begin{aligned} \varGamma _1&={\frac{-4\,\kappa \,{\omega _1}-4\,\alpha \,{\zeta }\sqrt{\frac{k_r}{m_r}}{\omega _1 }\, \left( \alpha -\varLambda _1\right) +4 \zeta { l_1}\,\beta \,{\omega _1}\, \left( \alpha -\varLambda _1 \right) }{4\,{\omega _1}\,{l_1}\,{\varLambda _1}+4\,{\omega _1}}}\\ \varGamma _2&=\frac{-\alpha _1(\alpha -\varLambda _2)^2(l_1m_r-\alpha )-q_{zr}}{4\omega _1(1+l_1\varLambda _1)}\\ \varGamma _3&=\frac{-2\,{\alpha _1}\, \left( \alpha -{{\bar{\varLambda }}_2}\right) \left( \alpha -{ l_1}\,{m_r} \right) \left( {\varPhi _1} -{\varPhi _2}\,\alpha \right) -2\,{q_{zr}}\,{\varPhi _2} }{4\omega _1(1+l_1\varLambda _1)}\\ \varGamma _4&=\frac{\alpha _1(\alpha -{\bar{\varLambda }}_2)(\alpha -\varLambda _1)(l_2m_r-\alpha )+q_{zr}}{2\omega _2(1+l_2\varLambda _2)}\\ \varGamma _5&=\frac{-{\alpha _1}\, \left( \alpha -{{\bar{\varLambda }}_1}\right) \left( \alpha -{ l_2}\,{m_r} \right) \left( {\varPhi _1} -{\varPhi _2}\,\alpha \right) -{q_{zr}}\,{\varPhi _2} }{2\omega _1(1+l_2\varLambda _2)}\\ \varGamma _6&={\frac{-2\,\alpha \,{\zeta }{\sqrt{\frac{k_r}{m_r}}}\,{\omega _2}\, \left( \alpha -{\varLambda _2} \right) +2\, \zeta \,{\varLambda _2}\,\beta \,{\omega _2}\, \left( \alpha -{\varLambda _2} \right) -2\,\kappa \,{\omega _2}}{2 \,{\omega _2}+2\,{\omega _2}\,{l_2}\,{\varLambda _2}}} \end{aligned}$$

Appendix F: linear stability of steady states

$$\begin{aligned}&\mathbf{J}_{P1}= \left[ \begin{array}{cccc} {\varGamma _1}&{}2\,{\varGamma _2}\,{\sin (\gamma ^{*}_1)}\, {a^{*}_2}&{}{\varGamma _2}\,{\cos (\gamma ^{*}_1)}\,{{a^{*}_2}}^{2}&{}{f_0}\,{\varGamma _3}\,{\cos (\gamma ^{*}_2)}\\ {\varGamma _4}\,{\sin (\gamma ^{*}_1)}\,{a^{*}_2}&{}{\varGamma _4}\,{\sin (\gamma ^{*}_1)}\,{a^{*}_1}+{\varGamma _5}&{}{\varGamma _4}\,{ \cos (\gamma ^{*}_1)}\,{a^{*}_2}\,{a^{*}_1}&{}0\\ {\frac{4\,{\varGamma _4}\,{\cos (\gamma ^{*}_1)}\,{a^{*}_1}+\sigma _2}{{a^{*}_1}}}&{}{\frac{2{\varGamma _2}\,{\cos (\gamma ^{*}_1)}\,{a^{*}_2}}{{a^{*}_1}}}&{}{\frac{-{\varGamma _2}\,{ \sin (\gamma ^{*}_1)}\,{{a^{*}_2}}^{2}-2\,{\varGamma _4}\,{\sin (\gamma ^{*}_1)}\,{{a^{*}_1}}^{2}}{{a^{*}_1}}}&{}-{\frac{{f_0}\,{\varGamma _3}\,{\sin (\gamma ^{*}_2}}{{a^{*}_1}}} \\ {\frac{{\sigma _1}}{{a^{*}_1}}}&{}\,{\frac{2{ \varGamma _2}\,{\cos (\gamma ^{*}_1)}\,{a^{*}_2}}{{a^{*}_1}}}&{}-{\frac{{\varGamma _2}\, {\sin (\gamma ^{*}_1}\,{{a^{*}_2}}^{2}}{{a^{*}_1}}}&{}-{\frac{{f_0}\,{\varGamma _3}\,{\sin (\gamma ^{*}_1)}}{{a^{*}_1}}}\end{array} \right] \,, \end{aligned}$$
(62)
$$\begin{aligned}&\mathbf{J}_{S1}= \left[ \begin{array}{cccc} {\varGamma _1}&{}2\,{\varGamma _2}\,{\sin (\gamma ^{*}_1)}\, {a^{*}_2}&{}{\varGamma _2}\,{\cos (\gamma ^{*}_1)}\,{{a^{*}_2}}^{2}&{}{f^2_0}\,{\varGamma _3}\,{\cos (\gamma ^{*}_2)}\\ {\varGamma _4}\,{\sin (\gamma ^{*}_1)}\,{a^{*}_2}&{}{\varGamma _4}\,{\sin (\gamma ^{*}_1)}\,{a^{*}_1}+{\varGamma _5}&{}{\varGamma _4}\,{ \cos (\gamma ^{*}_1)}\,{a^{*}_2}\,{a^{*}_1}&{}0\\ {\frac{4\,{\varGamma _4}\,{\cos (\gamma ^{*}_1)}\,{a^{*}_1}+\sigma _2}{{a^{*}_1}}}&{}{\frac{2{\varGamma _2}\,{\cos (\gamma ^{*}_1)}\,{a^{*}_2}}{{a^{*}_1}}}&{}{\frac{-{\varGamma _2}\,{ \sin (\gamma ^{*}_1)}\,{{a^{*}_2}}^{2}-2\,{\varGamma _4}\,{\sin (\gamma ^{*}_1)}\,{{a^{*}_1}}^{2}}{{a^{*}_1}}}&{}-{\frac{{f^2_0}\,{\varGamma _3}\,{\sin (\gamma ^{*}_2}}{{a^{*}_1}}} \\ {\frac{{\sigma _1}}{{a^{*}_1}}}&{}\,{\frac{2{ \varGamma _2}\,{\cos (\gamma ^{*}_1)}\,{a^{*}_2}}{{a^{*}_1}}}&{}-{\frac{{\varGamma _2}\, {\sin (\gamma ^{*}_1}\,{{a^{*}_2}}^{2}}{{a^{*}_1}}}&{}-{\frac{{f^2_0}\,{\varGamma _3}\,{\sin (\gamma ^{*}_1)}}{{a^{*}_1}}}\end{array} \right] \,. \end{aligned}$$
(63)
$$\begin{aligned}&\mathbf{J}_{P2}= \end{aligned}$$
(64)
$$\begin{aligned}&\quad \left[ \begin{array}{cccc} {\varGamma _1}&{}2{\varGamma _2}{\sin (\gamma ^{*}_1)} {a^{*}_2}&{}{\varGamma _2}{\cos (\gamma ^{*}_1)}{{a^{*}_2}}^{2}&{}0 \\ {\varGamma _4}{\sin (\gamma ^{*}_1)}{a^{*}_2}&{}{\varGamma _5}+{ \varGamma _4}{a^{*}_1}{\sin (\gamma ^{*}_1)}&{}{\varGamma _4}{a^{*}_1}{\cos (\gamma ^{*}_1)} {a^{*}_2}+{f_0}{\varGamma _3}{\cos (\gamma ^{*}_1)}&{}0\\ { \frac{-2{f_0}{\varGamma _3}{\cos (\gamma ^{*}_2)}+4{\varGamma _4}{a^{*}_1}{\cos (\gamma ^{*}_1)}{a^{*}_2}+\sigma _2{a^{*}_2}}{{a^{*}_2}{a^{*}_1}}}&{}{ \frac{3{\varGamma _2}{\cos (\gamma ^{*}_1)}{{a^{*}_2}}^{2}+\sigma _2{a^{*}_1}+2 {\varGamma _4}{{a^{*}_1}}^{2}{\cos (\gamma ^{*}_1)}}{{a^{*}_2}{a^{*}_1}}}&{}{ \frac{-2{\varGamma _4}{{a^{*}_1}}^{2}{\sin (\gamma ^{*}_1)}{a^{*}_2}-{\varGamma _2}{\sin (\gamma ^{*}_1)}{{a^{*}_2}}^{3}}{{a^{*}_2}{a^{*}_1}}}&{}2{\frac{{f_0}{\varGamma _3}{\sin (\gamma ^{*}_2)}}{{a^{*}_2}}}\\ -{\varGamma _4}{\cos (\gamma ^{*}_1)}&{}-{\frac{-{\sigma _1}+{\varGamma _4}{a^{*}_1}{\cos (\gamma ^{*}_1)}}{{a^{*}_2}}}&{}{\varGamma _4}{a^{*}_1}{\sin (\gamma ^{*}_1)}&{}-{\frac{ {f_0}{\varGamma _3}{\sin (\gamma ^{*}_2)}}{{a^{*}_2}}}\end{array} \right] \end{aligned}$$
(65)
$$\begin{aligned}&\mathbf{J}_{S2}= \end{aligned}$$
(66)
$$\begin{aligned}&\quad \left[ \begin{array}{cccc} {\varGamma _1}&{}2{\varGamma _2}{\sin (\gamma ^{*}_1)} {a^{*}_2}&{}{\varGamma _2}{\cos (\gamma ^{*}_1)}{{a^{*}_2}}^{2}&{}0 \\ {\varGamma _4}{\sin (\gamma ^{*}_1)}{a^{*}_2}&{}{\varGamma _5}+{ \varGamma _4}{a^{*}_1}{\sin (\gamma ^{*}_1)}&{}{\varGamma _4}{a^{*}_1}{\cos (\gamma ^{*}_1)} {a^{*}_2}+{{f_0}}^{2}{\varGamma _3}{\cos (\gamma ^{*}_1)}&{}0 \\ {\frac{\sigma _2{a^{*}_2}-2{{f_0}}^{2}{ \varGamma _3}{\cos (\gamma ^{*}_2)}+4{\varGamma _4}{a^{*}_1}{\cos (\gamma ^{*}_1)}{a^{*}_2 }}{{a^{*}_2}{a^{*}_1}}}&{}{\frac{2{\varGamma _4}{{a^{*}_1}}^{2}{ \cos (\gamma ^{*}_1)}+3{\varGamma _2}{\cos (\gamma ^{*}_1)}{{a^{*}_2}}^{2}+\sigma _2{a^{*}_1} }{{a^{*}_2}{a^{*}_1}}}&{}{\frac{-{\varGamma _2}{\sin (\gamma ^{*}_1)}{{a^{*}_2}} ^{3}-2{\varGamma _4}{{a^{*}_1}}^{2}{\sin (\gamma ^{*}_1)}{a^{*}_2}}{{a^{*}_2} {a^{*}_1}}}&{}2{\frac{{{f_0}}^{2}{\varGamma _3}{\sin (\gamma ^{*}_2)}}{{ a12}}}\\ -{\varGamma _4}{\cos (\gamma ^{*}_1)}&{}-{\frac{-{\sigma _1}+{\varGamma _4}{a^{*}_1}{\cos (\gamma ^{*}_1)}}{{a^{*}_2}}}&{}{\varGamma _4} {a^{*}_1}{\sin (\gamma ^{*}_1)}&{}-{\frac{{{f_0}}^{2}{\varGamma _3}{\sin (\gamma ^{*}_2)}}{{a^{*}_2}}}\end{array} \right] \end{aligned}$$
(67)
$$\begin{aligned}&\mathbf{J}_{C}= \left[ \begin{array}{cccc}C_{11}&{}C_{12}&{}C_{13}&{}C_{14}\\ C_{21}&{}C_{22}&{}C_{23}&{}C_{24}\\ C_{31}&{}C_{32}&{}C_{33}&{}C_{34}\\ C_{41}&{}C_{42}&{}C_{43}&{}C_{44} \end{array} \right] \, \end{aligned}$$
(68)

with

$$\begin{aligned}&C_{11}={\varGamma _1},\,C_{12}={\varGamma _3}{f_0}{ \sin (\gamma ^{*}_2)}+2{\varGamma _2}{\sin (\gamma ^{*}_1)}{a^{*}_2},\,\nonumber \\&C_{13}={\varGamma _2}{\cos (\gamma ^{*}_1)} {{a^{*}_2}}^{2},\,C_{14}={\varGamma _3}{f_0}{\cos (\gamma ^{*}_2)}{a^{*}_2},\nonumber \\&C_{21}={\varGamma _4}{\sin (\gamma ^{*}_1)}{a^{*}_2}+{f_0}{ \varGamma _5}{\sin (\gamma ^{*}_2)},\,\nonumber \\&C_{22}={\varGamma _6}+{\varGamma _4}{\sin (\gamma ^{*}_1)}{a^{*}_1},\,\nonumber \\&C_{23}={\varGamma _4}{\cos (\gamma ^{*}_1)}{a^{*}_2}{a^{*}_1},\,C_{24}={f_0}{\varGamma _5 }{\cos (\gamma ^{*}_2)}{a^{*}_1},\nonumber \\&C_{31}={\frac{4{\varGamma _4}{ \cos (\gamma ^{*}_1)}{a^{*}_2}{a^{*}_1}-4{f_0}{\varGamma _5}{\cos (\gamma ^{*}_2)} {a^{*}_1}+\sigma _2{a^{*}_2}}{{a^{*}_2}{a^{*}_1}}},\nonumber \\&C_{32}={\frac{3{\varGamma _2}{\cos (\gamma ^{*}_1)}{{a^{*}_2}}^{2}+\sigma _2{a^{*}_1}+2{\varGamma _4} {\cos (\gamma ^{*}_1)}{{a^{*}_1}}^{2}+2{\varGamma _3}{f_0}{\cos (\gamma ^{*}_2)}{ a^{*}_2}}{{a^{*}_2}{a^{*}_1}}},\nonumber \\&C_{33}={\frac{-2{\varGamma _4}{\sin (\gamma ^{*}_1)} {{a^{*}_1}}^{2}{a^{*}_2}-{\varGamma _2}{\sin (\gamma ^{*}_1)}{{a^{*}_2}}^{3}}{{ a^{*}_2}{a^{*}_1}}},\,\nonumber \\&C_{34}={\frac{2{f_0}{\varGamma _5}{\sin (\gamma ^{*}_2)} {{a^{*}_1}}^{2}-{\varGamma _3}{f_0}{\sin (\gamma ^{*}_2)}{{a^{*}_2}}^{2}}{ {a^{*}_2}{a^{*}_1}}}\nonumber \\&C_{41}=-{\frac{-2{f_0}{ \varGamma _5}{\cos (\gamma ^{*}_2)}{a^{*}_1}-{\sigma _1}{a^{*}_2}+2{\varGamma _4}{\cos (\gamma ^{*}_1)}{a^{*}_2}{a^{*}_1}}{{a^{*}_2}{a^{*}_1}}},\nonumber \\&C_{42}=-{ \frac{-3{\varGamma _2}{\cos (\gamma ^{*}_1)}{{a^{*}_2}}^{2}+{\varGamma _4}{ \cos (\gamma ^{*}_1)}{{a^{*}_1}}^{2}-{\sigma _1}{a^{*}_1}-2{\varGamma _3}{ f_0}{\cos (\gamma ^{*}_2)}{a^{*}_2}}{{a^{*}_2}{a^{*}_1}}},\nonumber \\&C_{43}=-{\frac{-{ \varGamma _4}{\sin (\gamma ^{*}_1)}{{a^{*}_1}}^{2}{a^{*}_2}+{\varGamma _2}{\sin (\gamma ^{*}_1)}{{a^{*}_2}}^{3}}{{a^{*}_2}{a^{*}_1}}},\nonumber \\&C_{44}=-{\frac{{f_0}{ \varGamma _5}{\sin (\gamma ^{*}_2)}{{a^{*}_1}}^{2}+{\varGamma _3}{f_0}{ \sin (\gamma ^{*}_2)}{{a^{*}_2}}^{2}}{{a^{*}_2}{a^{*}_1}}}\,. \end{aligned}$$
(69)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gupta, S.K., Bukhari, M.A. & Barry, O.R. Nonlinear mode coupling in a passively isolated mechanical system. Nonlinear Dyn 101, 2055–2086 (2020). https://doi.org/10.1007/s11071-020-05908-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-020-05908-9

Keywords

Search

Navigation