1 Introduction

In the modern world, the need for positioning or location–based services is gaining increasing attention. There are a variety of systems that are used in this field. The most important are Global Navigation Satellite Systems (GNSS). These systems provide an accurate (from a few meters to a few millimeters depending on technique and equipment), reliable position in Earth Centered Earth Fixed (ECEF) global coordinate system as well as precise time. Despite the many advantages of these systems, they have some drawbacks. Most important one is a necessity of line-of-sight between receiver and satellite. A lack of this requirement makes it impossible to perform positioning when the sky is obstructed. Despite the fact that GNSS is often augmented with other positioning systems (for example inertial measurement units (IMU) or pseudolites [17]), the gap in the scope of navigation must be filled using other positioning techniques. Since this gap has been studied by many research groups [10] hence, indoor positioning has recently become a popular topic in the area of navigation.

The development of radio frequency (RF) communication networks gives the possibility to use a physical layer (PHY) of these devices for positioning. Positioning in these networks can be divided into range-free and range-based techniques [11]. Radio signal strength indication (RSSI) is the most popular range-free technique. In this method empirical or theoretical model of the signal propagation is translated into position or distance estimates [5, 13, 19, 18, 7]. The range-based techniques are based on the measurement of distances between transceivers using time of arrival (TOA), time difference of arrival (TDOA) or round-trip time of flight (RToF) [7]. The phase measurement is a newly introduced method of distance measurement in RF networks [6]. This method can result with ranging accuracies of tenths of centimeters. With such an accuracy the impact of the choice of a mathematical tool used for computations starts to matter.

In range-based positioning, the distances between transceivers with a known location and user are used to estimate position in the trilateration (or multilateration) process. This is the most common approach to solve this task [8, 14, 12]. In the standard position estimation process (used for example in GNSS) the range equations are linearized. Linearization is performed using the first terms of Taylor series expansion. In this approach an initial guess of coordinates is required. In the case of GNSS the fraction \( \frac{coordinate\kern1em increase}{measured\kern1em distance} \) is very small since the satellites are ca. 20,000 km from the receiver.

In the case of indoor positioning this fraction can even be greater than 1 (when a coordinate increase is larger than measured distance). Therefore the initial estimate of coordinates has significant impact on positioning results and should be investigated. In this article the influence of the initial guess of coordinates on the positioning results is investigated on the basis of graphical interpretation of objective function. Graphical analysis can be a useful tool for studying the task of precise positioning. The example of such analysis can be found in [2].

In the next section the basis of the proposed positioning technique is presented. Section 3 concerns the mathematical model of the positioning technique. Section 4 is devoted to graphical interpretation of the objective function, which is the basis for the optimization process. In Section 5, three optimization techniques are presented. In Section 6, the experiment is described and the results of the tests are presented. Section 7 contains a discussion of the results and several conclusions are drawn from an analysis of the results.

2 Contribution of the work

This paper tries to visualize and analyze the impact of the choice of the computation technique on the results of range–based, indoor positioning. The visualization is made by presenting the shape of an objective function of the positioning task in a graphical form (as a 3D or contour plots). This visualization helps to explain the differences between two main groups of approaches: with and without linearization. Presented below least squares and Newton methods belong to the group of gradient zeroing methods, while Nelder – Mead method is a numerical approach. The latter method is more immune to the initial choice of coordinates than gradient zeroing methods. Localization–based services are more and more popular and demanding in the modern society. These services works very well in the outdoors environment where GNSS serves as the position provider. In the indoor environment this is a much more difficult task. Many approaches and research results are can be found in literature and the progress in the field of accuracy and availability can be observed. The approach to calculations performed during the positioning stage, are usually based on trilateration (or multilateration). Such a positioning task leads to a set of non-linear equations, which needs to be solved. The choice of the solution method is important from the wireless personal networks point of view (those with range–based positioning functionality), because it determines how much resources will be occupied and how reliable and accurate the result can be. The aspect of the choice of initial position is very important, because the positioning algorithm is “not aware” of where the user is at the moment of a start of the positioning device.

3 Basis of the range-based positioning technique using phase shift measurement

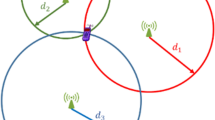
In range-based positioning, distances from rover to n fixed nodes with known coordinates (anchors) are measured and used to calculate rover position (Fig. 1). Unlike the TOA method, where distance is calculated on the basis of the time of signal arrival, in the phase shift method the carrier wave is modulated sinusoidally, and trip time is turned into phase shift:

$$ \varDelta \Phi =f\frac{d}{c} $$
(1)

where ∆Φ is the measured phase shift in cycles, f is the freyquency in Hz, d is the distance between nodes and rover in meters and c is the speed of light in meters per second. If we multiply the phase shift ∆Φ by wavelength:

$$ \lambda =\frac{c}{f} $$
(2)

we can obtain a geometric distance between rover and anchor:

$$ d=\Delta \Phi \lambda $$
(3)
Fig. 1
figure 1

Outline of range-base positioning geometry

Full size image

This method of ranging is used in the experiment presented in section 8. Usually the distances measured to different nodes have different accuracy. Therefore a proper weighting of observations must be introduced. This is done using adequate weight matrix. The position is then calculated on the basis of a 3D trilateration or multilateration. This technique requires an initial position of the rover. In practice the initial estimate of coordinates must be performed. It can be done in many various ways from arbitrary selection of coordinates (e.g., [0, 0, 0]), or using centroid of nodes to more sophisticated methods like preliminary trilateration. Depending on the environment and application the initial position can even be up to tens of meters away from the true position. In the next section, details of the mathematical model for positioning is described.

4 Mathematical model

Observation equations in range-based indoor navigation, in Cartesian 3D coordinate frame are described by Eq. 4.

$$ \left\{\begin{array}{l}{R}_1+{\xi}_1={\rho}_1=\sqrt{{\left({x}_1-X\right)}^2+{\left({y}_1-Y\right)}^2+{\left({z}_1-Z\right)}^2}\hfill \\ {}{R}_2+{\xi}_2={\rho}_2=\sqrt{{\left({x}_2-X\right)}^2+{\left({y}_2-Y\right)}^2+{\left({z}_2-Z\right)}^2}\hfill \\ {}\vdots \hfill \\ {}{R}_n+{\xi}_n={\rho}_n=\sqrt{{\left({x}_n-X\right)}^2+{\left({y}_n-Y\right)}^2+{\left({z}_n-Z\right)}^2}\hfill \end{array}\right. $$
(4)

where R 1 , R 2 , …, R n are observations from nodes, ρ 1 , ρ 2 , …, ρ n are geometric distances, ξ is a measurement error, X, Y, Z are rover coordinates and x 1 , y 1 , z 1 , x 2 , y 2 , z 2 , …, x n , y n , z n are node coordinates for nodes 1, 2, …, n respectively. Since these equations are not linear, it is required to expand them into Taylor series. For the equations to be linear, only first terms of this series are used. Using matrix notation:

$$ \xi =\mathrm{A}\mathrm{d}\mathrm{x}+\mathrm{l} $$
(5)
$$ \xi =\left[\begin{array}{c}\hfill {\xi}_1\hfill \\ {}\hfill {\xi}_2\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill {\xi}_n\hfill \end{array}\right];\kern1em \mathrm{d}\mathrm{x}=\left[\begin{array}{c}\hfill dX\hfill \\ {}\hfill dY\hfill \\ {}\hfill dZ\hfill \end{array}\right];\kern1em \mathrm{A}=\left[\begin{array}{ccc}\hfill \frac{\partial {\rho}_1}{\partial X}\hfill & \hfill \frac{\partial {\rho}_1}{\partial Y}\hfill & \hfill \frac{\partial {\rho}_1}{\partial Z}\hfill \\ {}\hfill \frac{\partial {\rho}_2}{\partial X}\hfill & \hfill \frac{\partial {\rho}_2}{\partial Y}\hfill & \hfill \frac{\partial {\rho}_2}{\partial Z}\hfill \\ {}\hfill \hfill & \hfill \vdots \hfill & \hfill \hfill \\ {}\hfill \frac{\partial {\rho}_n}{\partial X}\hfill & \hfill \frac{\partial {\rho}_n}{\partial Y}\hfill & \hfill \frac{\partial {\rho}_n}{\partial Z}\hfill \end{array}\right];\kern1em L=\left[\begin{array}{c}\hfill {\rho}_1^0-{R}_1\hfill \\ {}\hfill {\rho}_2^0-{R}_2\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill {\rho}_n^0-{R}_n\hfill \end{array}\right] $$
(6)

where ρ 01 , ρ 02 , … ρ 0 n are distances calculated on the basis of initial coordinates. After calculation of partial derivatives, matrix A yields the form:

$$ \mathrm{A}=\left[\begin{array}{ccc}\hfill \frac{x^0-{x}_1}{\rho_1^0}\hfill & \hfill \frac{y^0-{y}_1}{\rho_1^0}\hfill & \hfill \frac{z^0-{z}_1}{\rho_1^0}\hfill \\ {}\hfill \frac{x^0-{x}_2}{\rho_2^0}\hfill & \hfill \frac{y^0-{y}_2}{\rho_2^0}\hfill & \hfill \frac{z^0-{z}_2}{\rho_2^0}\hfill \\ {}\hfill \hfill & \hfill \vdots \hfill & \hfill \hfill \\ {}\hfill \frac{x^0-{x}_n}{\rho_n^0}\hfill & \hfill \frac{y^0-{y}_n}{\rho_n^0}\hfill & \hfill \frac{z^0-{z}_n}{\partial Z{\rho}_n^0}\hfill \end{array}\right] $$
(7)

where x 0 , y 0 , z 0 are initial rover coordinates. The least squares method, which is usually used, has the following objective function:

$$ \Psi ={\xi}^TP\xi = min $$
(8)

where P is a weight matrix. The solution of the set of Eq. 4 must be in the global minimum of this function.

5 Graphical representation of an objective function

As mentioned in the Introduction section, the impact of linearization of observation equations on the behavior of objective function is substantial in the case of small distances [4], especially in the case of poor accuracy of initial position. It means that the impact of a linearization can be so significant, that the computations will converge to a wrong solution. Therefore the accuracy of initial coordinates is important in case of standard optimization methods. Another option is to use a method which is resistant (to certain extent) to the choice of initial coordinates. Therefore it is important to investigate the shape and behavior of an objective function. This can be done using a graphical representation of this function in the form of 3D surface. In order to depict the objective function, the values of this function must be calculated in the area surrounding the correct solution. To compare objective function before and after linearization, its graphical representation in both options can be created. Graphical analysis can be useful in studies on the optimization process. Particularly for depicting the initial, final and true position against objective function behavior (represented by the 3D surface). The values of linearized objective function are calculated using Eqs. 5–8. These values are calculated in the grid formed in the area around the solution. In the case of a non-linearized objective function the values are calculated using (8) with ξ defined as:

$$ \xi =\left[\begin{array}{c}\hfill {\rho}_1-{R}_1\hfill \\ {}\hfill {\rho}_2-{R}_2\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill {\rho}_n-{R}_n\hfill \end{array}\right] $$
(9)

6 Algorithms

Three algorithms of finding a function minimum are presented in this section.

  1. A.

    Standard least squares

In this approach the increments to the initial coordinates are calculated as:

$$ \mathrm{d}\mathrm{x}=-{\left({\mathrm{A}}^T\mathrm{P}\mathrm{A}\right)}^{-1}{\mathrm{A}}^T\mathrm{P}\mathrm{l} $$
(10)

Next the value of objective function is calculated using Eqs. 5 and 8. This process is performed in iterations. In each iteration matrices A and l are updated using results from previous iteration:

$$ {\mathrm{X}}_i={\mathrm{X}}_{i-1}-{\left({\mathrm{A}}_{i-1}^T{\mathrm{PA}}_{i-1}\right)}^{-1}{\mathrm{A}}_{i-1}^T{\mathrm{Pl}}_{i-1} $$
(11)

Iteration process stops when the change in the objective function value is smaller than one percent of its initial value.

  1. B.

    Newton method

Newton method is an iterative algorithm of finding the minimum of a twice-differentiable function. In each step the objective function is approximated with a quadratic function:

$$ {\Psi}_a=\mathrm{G}\mathrm{d}\mathrm{x}+\frac{1}{2}{\mathrm{dx}}^T\mathrm{H}\mathrm{d}\mathrm{x} $$
(12)

Zeroing the gradient of the Ψ a function, the following formula of the optimization process is obtained [3, 1, 16, 9]:

$$ {\mathrm{x}}_i={\mathrm{x}}_{i-1}-{\mathrm{H}}_{i-1}^{-1}{\mathrm{G}}_{i-1} $$
(13)

where G and H are gradient and Hessian of the objective function computed on the basis of x from a previous iteration. The gradient of the objective function Ψ is expressed by the formula:

$$ \mathrm{G}=\frac{\partial \Psi}{\partial \mathrm{x}}=2{\xi}^T\mathrm{P}\mathrm{A} $$
(14)

The Hessian can be formed as:

$$ \mathrm{H}=\frac{\partial^2\Psi}{\partial {\mathrm{x}}^2}=\frac{\partial \mathrm{G}}{\partial \mathrm{x}}=2{\mathrm{A}}^T\mathrm{P}\mathrm{A} $$
(15)

Thus, formula 13 takes form:

$$ {\mathrm{x}}_i={\mathrm{x}}_{i-1}-{\left({\mathrm{A}}^T\mathrm{P}\mathrm{A}\right)}^{-1}{\mathrm{A}}^T\mathrm{P}{\xi}_{i-1} $$
(16)
$$ {\xi}_0=\mathrm{l} $$
(17)

As we can see, the first iteration is simply the least squares solution.

  1. C.

    Nelder-Mead simplex

The search for a minimum of objective function can be performed using a numerical method called the Nelder-Mead simplex [15]. This method searches for a correct solution in a large area, so the problem of initial coordinates is not crucial. In this method, the search for the minimum of the objective function is based on the simplex transformations (Fig. 2). Since the method is based on calculation of function values directly from non-linear formulas, no linearisation is required.

Fig. 2
figure 2

Simplex transformations

Full size image

At the initial stage the simplex is formed, assuming a certain distance between the vertices (the default is five percent of the parameter value). The simplex transformations are carried out until the distance between the vertices is less than the value of the assumed criterion. During the procedure simplex is modified many times, until it reaches the global minimum. In procedure of searching for the minimum of objective function the following operations are applied: calculating the center of gravity of the simplex, reflection, expansion, outer and inner contraction and shrinkage.

Each of the proposed approaches can fit into the algorithm presented in Fig. 3.

Fig. 3
figure 3

Algorithm scheme

Full size image

Initial coordinates of the user, coordinates of nodes and measured distances serves as an input to the algorithm. In each iteration the calculations are performed using one of the methods described above. If the iteration end criterion is not satisfied, the results are used as the input for the next iteration. If the iteration end criterion is satisfied, the calculation process is finished and the results are returned.

7 Test site, equipment and experiment results

For the purpose of this article, the network of nodes presented in Fig. 4 was prepared. The distances in Fig. 4 are reference distances measured with a laser range-finder. The node coordinates were determined by geodetic techniques. To minimize the influence of multipath the experiment was conducted in an obstacle–free environment, and nodes were placed about 1.5 m above the ground. The measurements were performed using REB233SMAD evaluation kits based on the AT86RF233 2.4GHz ZigBee transceivers (from ATMEL). In this device next to the TOF module, a phase measurement unit (PMU) is introduced. This feature brings a significant improvement in the distance measurement accuracy using a RF communication network. For the purpose of this paper, four nodes (1, 2, 3, 4) were stationary nodes with known coordinates, and the fifth node was treated as a rover with an unknown position. The rover device was connected to the PC using serial communication at 38,400 baud rate. The rover device was measuring distances to each of the stationary nodes using peer to peer communication. For each node ranging took about 165 ms. All of the nodes were operating on 2xAAA batteries. During ranging Tx power for this devices is about -17dBm. Power consumption during sleep for this devices is at 17 μA. In the TRX state (oscillator is on) it consumes 15 mA, 28 mA while receiving and 26 mA during transmit. One of the devices used in this experiment is depicted in Fig. 5.

Fig. 4
figure 4

Test site geometry

Full size image
Fig. 5
figure 5

REB233SMAD device

Full size image

The measurements were repeated 300 times for each distance and the mean value was used as a measurement result. The distance quality factor (DQF) was used to weight the observations. DQF is a parameter provided by evaluation software. Although it reflects the percentage of correct distance measurements, no details on this parameter are available in the data sheet [6]. Table 1 summarizes the results of the measurements, ∆d is calculated as the difference of the measured distance minus reference distance. It can be seen that the accuracy of the measurements is much better from the one obtained from most commonly used RSSI based method (which error can be as large as few meters [20]).

Table 1 Summary of distance measurement
Full size table

Table 2 contains the results of optimization using three techniques. The last column contains the geometric distances between reference and calculated positions. In the case of the LS method, the distance ∆d from the reference position to the solution is 2.97 m. For the Newton method it is 1.81 m. The best result was obtained using the N-M method. In this case ∆d = 0.70 m. This 70 cm displacement is entirely in the height component of user position. This is caused by the poor vertical distribution of the nodes (all of the nodes at the same height).

Table 2 Summary of the results
Full size table

For 3D positioning, plotting of an objective function would require a 4 dimensional plot (X, Y, Z, Ψ). Therefore, only a cross–section can be plotted. For the purpose of this article it will be a cross– section in Z = 100 (which is a correct Z coordinate of the rover). Figure 6 depicts the linearized objective function (computed from 5 and 8) while Fig. 7 depicts the original, not linearized objective function (computed from 4 and 8). In both of these figures, the surface represents the shape of the objective function with its contour lines projected on the XY plane. For each X and Y coordinate a sum of the residuals is computed and depicted in this figures. The linearized function is much smoother with no local minimums. Before linearization, the function has many local minima so the solution based on the gradient optimization method can lead to one of them instead of the global minimum.

Fig. 6
figure 6

Objective function after linearization

Full size image
Fig. 7
figure 7

Objective function

Full size image

To depict the influence of linearization on objective function, the non-linearized plot is depicted in Fig. 7.

Figures 8, 9, 10, depicts the solution for three calculation methods with a poor choice of initial coordinates. Figures 11, 12, 13 depicts the solution for three calculation methods with a good choice of initial coordinates. The right side of these figures depicts the square from the left side. Contour lines on the left side of each figure depicts the not–linearized objective function. Solid line depicts how the solution “travels” from the initial coordinates to the final solution with each iteration. In figures with good initial coordinates the case with the initial coordinates in the centroid of nodes is presented. In figure with poor choice of initial coordinates, the initial coordinates are close to anchor number 3. In both cases the results from the LS and Newton methods are very similar (considering the required accuracy).

Fig. 8
figure 8

Least squares solution iterations with poor initial coordinates

Full size image
Fig. 9
figure 9

Newton solution iterations with poor initial coordinates

Full size image
Fig. 10
figure 10

Nelder-Mead solution iterations with poor initial coordinates

Full size image
Fig. 11
figure 11

Least squares solution iterations with good initial coordinates

Full size image
Fig. 12
figure 12

Newton solution iterations with good initial coordinates

Full size image
Fig. 13
figure 13

Nelder-Mead solution iterations with good initial coordinates

Full size image

The distance from the true position to the solutions in each iteration is depicted in Figs. 14 and 15. These Figures depict the convergence of the solution for each method. For the LS and Newton methods the solution is not stable. In the investigated case, better guess (assumption) of initial coordinates did not improve the stability of the solution. The Nelder–Mead method converges in 8 iterations, and is stable.

Fig. 14
figure 14

Distances to true position in each iteration case No. 1

Full size image
Fig. 15
figure 15

Distances to true position in each iteration case No. 2

Full size image

8 Discussion

Comparison of three techniques of solving non-linear set of equations in the range–based indoor positioning was performed. For such positioning the initial estimate of coordinates has a significant impact on the solution. In order to present the influence of initial assumptions (namely optimization algorithm and choice of initial coordinates) on the indoor, range–based positioning results, a case study was analyzed. In the presented example a new ZigBee ranging method (based on phase shift measurement) was used. The application of PMU for ranging allowed to obtain much better accuracy of ranging than for the RSSI or TOA methods. With this relatively high accuracies, the impact of the choice of both algorithm and the initial position is significant. To depict this issue, in order to present the shape of objective function of positioning task, contour plots and 3D visualizations are presented.

In the presented case study, the initial position was about 20 m away from the true position (close to node no. 3). This was the reason why the algorithms based on gradient optimization techniques failed to obtain a correct solution. On the other hand, a numerical Nelder– Mead method found a solution very close to the true position of the rover.

When the initial position was in the centroid of nodes the difference between solutions was much smaller. At the same time the Nelder-Mead algorithm also gave the correct solution.

The case study points out that the presented positioning technique is very sensitive to the accuracy of the initial position. In such a case the gradient methods failed in searching for the solution. The solution was unstable and resulted in incorrect position. Therefore the numerical technique (Nelder–Mead method) is recommended for optimization of the objective function.