Skip to main content
SpringerLink
Log in

Study of vibration characteristics for orthotropic circular cylindrical shells using wave propagation approach and multivariate analysis

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

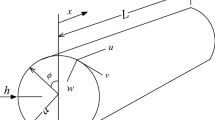
A study of free vibration of orthotropic circular cylindrical shells is presented. The vibration control equations of shells are based on Flügge classical thin shell theory. Wave approach is used in the analysis, in which the boundary conditions of shells can be simplified according to the associated beam. The free vibration frequencies of shells can be obtained from a frequency polynomial equation of order 6. The parametric analysis of the free vibration of orthotropic cylindrical shells is investigated using a statistical method. The effects of geometrical parameters and material characteristics upon frequencies are investigated here. Multivariate analysis (MVA) can be a useful tool for this parametric study. Some statistical characteristics, including correlation analysis and ANOVA are applied. ANOVA has been conducted to predict the statistical significance of the various factors. Calculations are performed in the Minitab statistical software. The results show that the L/R, h/R and m have larger effects on the lowest frequency. The importance of input parameters is ranked according to their contributions to the total variance. A knowledge and data visualization approach, Self-organizing mapping (SOM) is also adopted here for mining some intrinsic characteristics of shells.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Leissa AW (1993) Vibration of shells (NASA SP 288). US Government Printing Office, Washington, DC

    Google Scholar 

  2. Liu B, Xing YF, Qatu MS et al (2012) Exact characteristic equations for free vibrations of thin orthotropic circular cylindrical shells. Compos Struct 94(2):484–493

    Article  Google Scholar 

  3. Agalovyan LA, Gulgazaryan LG (2006) Asymptotic solutions of non-classical boundary-value problems of the natural vibrations of orthotropic shells. J Appl Math Mech 70(1):102–115

    Article  MathSciNet  MATH  Google Scholar 

  4. Li X (2008) Study on free vibration analysis of circular cylindrical shells using wave propagation. J Sound Vib 311(3–5):667–682

    Google Scholar 

  5. Montgomery DC, Runger GC (2003) Applied statistics and probability for engineers. Wiley, New York

    MATH  Google Scholar 

  6. Walpole RE, Myers RH, Myers SL et al (2010) Probability and statistics for engineers and scientists. Prentice Hall, Boston

    MATH  Google Scholar 

  7. Johnson RA, Wichern DW (2007) Applied multivariate statistical analysis, 6th edn. Prentice Hall, New Jersey

    MATH  Google Scholar 

  8. Timm NH (2001) Applied multivariate analysis. Springer, New York

    MATH  Google Scholar 

  9. Minitab Inc (2013) Minitab statistical software, release 17

  10. Kohonen T (1982) Self-organized formation of topologically correct feature maps. Biol Cybermetircs 43(1):59–69

    Article  MATH  Google Scholar 

  11. Kohonen T (2013) Essentials of the self-organizing map. Neural Netw 37(1):52–65

    Article  Google Scholar 

  12. Harris CM, Piersol AG (2002) Harris’ shock and vibration handbook. McGraw Hill, New York

    Google Scholar 

  13. Phadke MS (1989) Quality engineering using robust design. AT&T Bells Laboratory/Prentice-Hall, New Jersey

    Google Scholar 

  14. Vesanto J, Alhoniemi E (2000) Clustering of the self-organizing map. IEEE Trans Neural Netw 11(3):586–600

    Article  Google Scholar 

  15. Kohonen T (2001) Self-organizing maps, 3rd edn. Springer, Berlin

    Book  MATH  Google Scholar 

  16. Vesanto J (2002) Data exploration process based on the self-organizing map. Ph.D. Thesis. Helsinki University of Technology, Espoo

  17. Warburton GB, Soni SR (1977) Resonant response of orthotropic cylindrical shells. J Sound Vib 53(1):1–23

    Article  ADS  MATH  Google Scholar 

  18. Ultsch A, Siemon HP (1990) Kohonen’s self-organizing feature maps for exploratory data analysis. In: Proceedings of the international neural network conference (INNC’90). Dordrecht

  19. Ultsch A (2003) Maps for the visualization of high-dimensional data spaces. In: Proceedings of the workshop on self organizing maps. Kyushu

  20. Ultsch A (2003) U*-matrix: a tool to visualize clusters in high dimensional data. Department of Computer Science, University of Marburg, Marburg

    Google Scholar 

  21. Nisbet R, Elder J, Miner C (2009) Handbook of statistical analysis and data mining applications. Elsevier Inc, London

    MATH  Google Scholar 

  22. Davies DL, Bouldin DW (1979) A cluster separation measure. IEEE Trans Pattern Recognit Mach Intell 1(2):224–227

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Wuhan 2nd Ship Design and Research Institute, Wuhan, 430064, Hubei Province, People’s Republic of China

    Xuebin Li, Zhiqiang Wang & Lihua Huang

Authors
  1. Xuebin Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhiqiang Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Lihua Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xuebin Li.

Appendix

Appendix

$${\text{g}}_{6} = \frac{{h^{3} R^{6} \rho^{3} }}{{D_{x}^{3} }}$$
$$\begin{aligned} {\text{g}}_{4} = & - \frac{1}{{D_{x}^{3} }}h^{2} R^{2} \rho^{2} \left( {\left( {1 + n^{2} } \right)R^{2} D_{\theta } - 3PR^{4} k_{\text{ns}}^{2} + R^{4} D_{x} k_{\text{ns}}^{2} + R^{2} D_{{{\text{x}}\uptheta}} \left( {n^{2} + R^{2} k_{\text{ns}}^{2} } \right) + R^{4} k_{\text{ns}}^{4} K_{x} + n^{2} K_{{{\text{x}}\uptheta}} } \right. \\ & \;\left. { +\,3R^{2} k_{\text{ns}}^{2} K_{{{\text{x}}\uptheta}} + 4n^{2} R^{2} k_{\text{ns}}^{2} K_{{{\text{x}}\uptheta}} + K_{\theta } - 2n^{2} K_{\theta } + n^{4} K_{\theta } + n^{2} R^{2} k_{\text{ns}}^{2} K_{\theta } \nu_{x} + n^{2} R^{2} k_{\text{ns}}^{2} K_{x} \nu_{\theta } } \right) \\ \end{aligned}$$
$$g_{2} = \frac{1}{{R^{2} D_{x}^{3}}}h\rho ({3P^{2} R^{8} k_{\text{ns}}^{4} - 2PR^{8} D_{x} k_{\text{ns}}^{4} - 2PR^{8} k_{\text{ns}}^{6} K_{x} + R^{8} D_{x} k_{\text{ns}}^{6} K_{x} - R^{6} k_{\text{ns}}^{6} K_{x}^{2} - 2n^{2} PR^{4} k_{\text{ns}}^{2} K_{{{\text{x}}{\uptheta}}}} - 6PR^{6} k_{\text{ns}}^{4} K_{{{\text{x}}{\uptheta}}} - 8n^{2} PR^{6} k_{\text{ns}}^{4} K_{{{\text{x}}{\uptheta}}} + 3R^{6} D_{x} k_{\text{ns}}^{4} K_{{{\text{x}}{\uptheta}}} + 4n^{2} R^{6} D_{x} k_{\text{ns}}^{4} K_{{{\text{x}}{\uptheta}}} + 3n^{2} R^{4} k_{\text{ns}}^{4} K_{x} K_{{{\text{x}}{\uptheta}}} + 3R^{6} k_{\text{ns}}^{6} K_{x} K_{{{\text{x}}{\uptheta}}} + 3n^{2} R^{2} k_{\text{ns}}^{2} K_{{{\text{x}}{\uptheta}}}^{2} + 3n^{4} R^{2} k_{\text{ns}}^{2} K_{{{\text{x}}{\uptheta}}}^{2} + 3n^{2} R^{4} k_{\text{ns}}^{4} K_{{{\text{x}}{\uptheta}}}^{2} - 2PR^{4} k_{\text{ns}}^{2} K_{\theta} + 4n^{2} PR^{4} k_{\text{ns}}^{2} K_{\theta} - 2n^{4} PR^{4} k_{\text{ns}}^{2} K_{\theta} + R^{4} D_{x} k_{\text{ns}}^{2} K_{\theta} - 2n^{2} R^{4} D_{x} k_{\text{ns}}^{2} K_{\theta} + n^{4} R^{4} D_{x} k_{\text{ns}}^{2} K_{\theta} + n^{2} K_{{{\text{x}}{\uptheta}}} K_{\theta} - 2n^{4} K_{{{\text{x}}{\uptheta}}} K_{\theta} + n^{6} K_{{{\text{x}}{\uptheta}}} K_{\theta} + 3R^{2} k_{\text{ns}}^{2} K_{{{\text{x}}{\uptheta}}} K_{\theta} - 6n^{2} R^{2} k_{\text{ns}}^{2} K_{{{\text{x}}{\uptheta}}} K_{\theta} + 3n^{4} R^{2} k_{\text{ns}}^{2} K_{{{\text{x}}{\uptheta}}} K_{\theta} - 2n^{2} PR^{6} k_{\text{ns}}^{4} K_{\theta} \nu_{x} + n^{2} R^{6} D_{x} k_{\text{ns}}^{4} K_{\theta} \nu_{x} + n^{4} R^{2} k_{\text{ns}}^{2} K_{{{\text{x}}{\uptheta}}} K_{\theta} \nu_{x} - 2n^{2} PR^{6} k_{\text{ns}}^{4} K_{x} \nu_{\theta} - R^{6} D_{x} k_{\text{ns}}^{4} K_{x} \nu_{\theta} + n^{2} R^{6} D_{x} k_{\text{ns}}^{4} K_{x} \nu_{\theta} + n^{2} R^{4} D_{x} k_{\text{ns}}^{2} K_{{{\text{x}}{\uptheta}}} \nu_{\theta} + n^{4} R^{2} k_{\text{ns}}^{2} K_{x} K_{{{\text{x}}{\uptheta}}} \nu_{\theta} - n^{2} R^{4} k_{\text{ns}}^{4} K_{x} K_{\theta} \nu_{x} \nu_{\theta} + R^{2} D_{{{\text{x}}{\uptheta}}} ({R^{6} k_{\text{ns}}^{6} K_{x} + n^{2} ({- 1 + n^{2}})^{2} K_{\theta} + R^{2} D_{\theta} ({n^{2} + n^{4} + R^{2} k_{\text{ns}}^{2} ({1 - n^{2} \nu_{x}})})} + R^{4} k_{\text{ns}}^{4} ({- 2PR^{2} + R^{2} D_{x} + 4n^{2} K_{{{\text{x}}{\uptheta}}} + n^{2} K_{\theta} \nu_{x} + n^{2} K_{x} ({1 + \nu_{\theta}})}) + {R^{2} k_{\text{ns}}^{2} ( {4({n^{2} + n^{4}})K_{{{\text{x}}{\uptheta}}} + K_{\theta} ({({- 1 + n^{2}})^{2} + n^{4} \nu_{x}}) + n^{2} ({- 2PR^{2} - R^{2} D_{x} \nu_{\theta} + n^{2} K_{x} \nu_{\theta}})})}) + R^{2} D_{\theta} ({n^{2} ({( {1 + n^{2}})K_{{{\text{x}}{\uptheta}}} + ({- 1 + n^{2}})^{2} K_{\theta}})} + R^{4} k_{\text{ns}}^{4} K_{x} ({n^{2} - \nu_{x}}) + R^{2} k_{\text{ns}}^{2} ({- 2PR^{2} - 2n^{2} PR^{2} - n^{2} K_{\theta} \nu_{x}} { {{+ n^{4} K_{\theta} \nu_{x} + K_{{{\text{x}}{\uptheta}}} ({3 - 6n^{2} + 4n^{4} + n^{2} \nu_{x}}) - n^{2} K_{x} \nu_{\theta} + n^{4} K_{x} \nu_{\theta} - ({1 + n^{2}})R^{2} D_{x} ({- 1 + \nu_{x} \nu_{\theta}})})})})$$
$$g_{0} = \frac{1}{{R^{4} D_{x}^{3}}}(D_{\theta} (- n^{4} ({- 1 + n^{2}})^{2} K_{{{\text{x}}{\uptheta}}}K_{\theta} + R^{6} k_{\text{ns}}^{6} K_{x} (n^{2} PR^{2} - PR^{2} \nu_{x} + 3K_{{{\text{x}}{\uptheta}}} \nu_{x} - 3n^{2} K_{{{\text{x}}{\uptheta}}} \nu_{x} +n^{2} K_{x} ({1 - \nu_{x} \nu_{\theta}})+ n^{2} R^{2} D_{x} ({- 1 + \nu_{x} \nu_{\theta}})) + R^{4} k_{\text{ns}}^{4} (3n^{2} ({- 1 + n^{2}})K_{{{\text{x}}{\uptheta}}}^{2} \nu_{x} - PR^{2} (({1 + n^{2}})PR^{2} - n^{2} ({- 1 + n^{2}})K_{\theta} \nu_{x} - n^{2} ({- 1 + n^{2}})K_{x} \nu_{\theta}) - R^{2} D_{x} (PR^{2} + n^{2} PR^{2} + ({- 3 +6n^{2} - 4n^{4}})K_{{{\text{x}}{\uptheta}}} - n^{2} ({- 1 +n^{2}})K_{\theta} \nu_{x} + n^{2} K_{x} \nu_{\theta} - n^{4} K_{x} \nu_{\theta})({- 1 + \nu_{x}\nu_{\theta}}) + K_{{{\text{x}}{\uptheta}}} ({PR^{2} ({3 -6n^{2} + 4n^{4} + n^{2} \nu_{x}}) + n^{4} K_{x} ({- 3 + \nu_{x} \nu_{\theta}})})) +n^{2} R^{2} k_{\text{ns}}^{2} (- 3({- 1 + n^{2}})^{2}K_{{{\text{x}}{\uptheta}}}^{2} + K_{{{\text{x}}{\uptheta}}} ({({1 + n^{2}})PR^{2} - n^{2} ({- 1 + n^{2}})K_{\theta} \nu_{x} - n^{2} ({- 1 + n^{2}})K_{x} \nu_{\theta}}) + ({- 1 + n^{2}})^{2} R^{2}K_{\theta} ({P + D_{x} ({- 1 + \nu_{x} \nu_{\theta}})}))) + k_{\text{ns}}^{2} (- R^{6} k_{\text{ns}}^{6} K_{x}({PR^{2} - R^{2} D_{x} + K_{x}})({PR^{2} -3K_{{{\text{x}}{\uptheta}}}}) + n^{2} ({- 1 + n^{2}})^{2} ({PR^{2} - 3K_{{{\text{x}}{\uptheta}}}})K_{{{\text{x}}{\uptheta}}} K_{\theta} + R^{4} k_{\text{ns}}^{4} (PR^{2} ({- ({3 +4n^{2}})PR^{2}+ 3n^{2} K_{x}})K_{{{\text{x}}{\uptheta}}} + 3n^{2} (PR^{2}- 3K_{x})K_{{{\text{x}}{\uptheta}}}^{2} + PR^{2} ({- n^{2} K_{\theta}\nu_{x} ({PR^{2} + K_{x} \nu_{\theta}}) + PR^{2}({PR^{2} - n^{2} K_{x} \nu_{\theta}})}) +R^{2} D_{x} (- 3n^{2} K_{{{\text{x}}{\uptheta}}}^{2} + K_{{{\text{x}}{\uptheta}}} ((3 + 4n^{2})PR^{2} - 3({- 1 + n^{2}})K_{x} \nu_{\theta}) + PR^{2} ({- PR^{2} + n^{2}K_{\theta} \nu_{x} + ({- 1 + n^{2}})K_{x} \nu_{\theta}}))) + k_{\text{ns}}^{2} (- ({- 1+ n^{2}})^{2} PR^{6} ({P - D_{x}})K_{\theta}+ 3n^{2} R^{4} K_{{{\text{x}}{\uptheta}}}^{2} ({({1 + n^{2}})P + ({- 1 + n^{2}})D_{x} \nu_{\theta}}) + K_{{{\text{x}}{\uptheta}}} (n^{2} PR^{4} (- PR^{2} +R^{2} D_{x} \nu_{\theta} + n^{2} K_{x} \nu_{\theta}) +K_{\theta} (3({- 1 + n^{2}})^{2} PR^{4} + n^{4}R^{2} \nu_{x} ({PR^{2} + K_{x} \nu_{\theta}}) +R^{4} D_{x} (- 3({- 1 + n^{2}})^{2} +n^{4} \nu_{x} \nu_{\theta}))))) + R^{2} D_{{{\text{x}}{\uptheta}}}(D_{\theta} (- n^{4} ({- 1 + n^{2}})^{2} K_{\theta} + ({1 + n^{2}})R^{6} k_{\text{ns}}^{6} K_{x} \nu_{x}+ n^{2} R^{2} k_{\text{ns}}^{2} (PR^{2} + n^{2} PR^{2} -4({- 1 + n^{2}})^{2} K_{{{\text{x}}{\uptheta}}} - ({- 1+ n^{2}})K_{\theta} \nu_{x} + n^{2} K_{x} \nu_{\theta}- n^{4} K_{x} \nu_{\theta}) + R^{4} k_{\text{ns}}^{4} (PR^{2} -n^{2} PR^{2} \nu_{x} - 4n^{2} K_{{{\text{x}}{\uptheta}}} \nu_{x}+ 4n^{4} K_{{{\text{x}}{\uptheta}}} \nu_{x} - n^{2} K_{\theta} \nu_{x}^{2} +n^{4} K_{\theta} \nu_{x}^{2} + R^{2} D_{x} ({- 1 + \nu_{x} \nu_{\theta}}) + n^{2} K_{x} ({- 2 - n^{2} +n^{2} \nu_{x} \nu_{\theta}}))) +k_{\text{ns}}^{2} (R^{6} k_{\text{ns}}^{6} K_{x} ({PR^{2} - R^{2} D_{x}+ K_{x}}) + n^{2} ({- 1 + n^{2}})^{2}K_{\theta} ({- 4K_{{{\text{x}}{\uptheta}}} + R^{2} ({P + D_{x}\nu_{\theta}})}) + R^{4} k_{\text{ns}}^{4} (PR^{2} (-PR^{2} + 4n^{2} K_{{{\text{x}}{\uptheta}}} + n^{2} K_{\theta}\nu_{x}) - n^{2} K_{x}^{2} \nu_{\theta} + R^{2} D_{x} ({PR^{2} - 4n^{2} K_{{{\text{x}}{\uptheta}}} - n^{2} K_{\theta} \nu_{x} +K_{x} \nu_{\theta}}) + n^{2} K_{x} (- 12K_{{{\text{x}}{\uptheta}}} -K_{\theta} \nu_{x} + PR^{2} ({1 + \nu_{\theta}}))) + k_{\text{ns}}^{2} (4n^{2} R^{4} K_{{{\text{x}}{\uptheta}}} ({({1 + n^{2}})P + ({- 1 + n^{2}})D_{x}\nu_{\theta}}) + n^{2} R^{4} (P({- PR^{2} + n^{2}K_{x} \nu_{\theta}}) + D_{x} \nu_{\theta}({- PR^{2} + ({- 1 + n^{2}})K_{x} \nu_{\theta}})) + K_{\theta} (({- 1 + n^{2}})^{2} PR^{4} + n^{4} R^{2} \nu_{x} ({PR^{2} + K_{x}\nu_{\theta}}) + R^{4} D_{x} ({-({- 1 + n^{2}})^{2} + n^{4} \nu_{x} \nu_{\theta}}))))))$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, X., Wang, Z. & Huang, L. Study of vibration characteristics for orthotropic circular cylindrical shells using wave propagation approach and multivariate analysis. Meccanica 52, 2349–2361 (2017). https://doi.org/10.1007/s11012-016-0587-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-016-0587-8

Keywords

Search

Navigation