On the behavior of a three-dimensional fractional viscoelastic constitutive model

Abstract

In this paper a three-dimensional isotropic fractional viscoelastic model is examined. It is shown that if different time scales for the volumetric and deviatoric components are assumed, the Poisson ratio is time varying function; in particular viscoelastic Poisson ratio may be obtained both increasing and decreasing with time. Moreover, it is shown that, from a theoretical point of view, one-dimensional fractional constitutive laws for normal stress and strain components are not correct to fit uniaxial experimental test, unless the time scale of deviatoric and volumetric are equal. Finally, the model is proved to satisfy correspondence principles also for the viscoelastic Poisson’s ratio and some issues about thermodynamic consistency of the model are addressed.

Appendix

The thermodynamic consistency of fractional viscoelastic model has been widely investigated and demonstrated by several authors (see e.g. [31, 32, 34, 35]). In this “Appendix” two cases are studied in order to further confirm the results of other authors, a relaxation test and a dynamic test.

The thermodynamic consistency is usually investigated by imposing non-negative internal work (elastic energy stored in the solid) and non-negative rate of energy dissipation and if these hold what restrictions apply to its parameters in order to respect the conditions. In classical models the internal work is related to the stored energy in the solid, then to the elastic part of strain; the dissipated energy is related to the viscous part of the strain. However in fractional viscoelasticity is not possible to distinguish between elastic and inelastic strain; this is due to the the fact that the springpot model contains in itself the features of both spring and dashpot, as shown by the hierarchical or selfsimilar models that are able to reproduce power law viscoelasticity [11, 29, 30]. To overcome this problem, it is possible to work with state functions and in particular with the concept of free energy (corresponding to the elastic energy) and dissipation rates; indeed, in the paper [36] it has been found what is the right definition of the free energy for the springpot model shown in the following. In this way the free energy itself and the dissipation rate can be evaluated.

The specific Helmotz free energy $\psi$ is a thermodynamic state function whose gradient with respect to the actual value of strain $\varepsilon$ gives the measured stress; it represents the energy stored in the solid, that is what in elasticity is defined as elastic energy. The rate of free energy can be expressed as follows:

Fig. 7

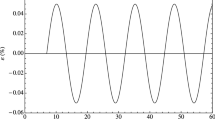
Applied strain histories for the evaluation of free energy and dissipation rate with Eq. (43): sinusoidal (a) and constant with initial linear ramp (b)

$$\begin{aligned} \dot{\psi }=\dot{u}-T \dot{s} \end{aligned}$$

(39)

where $\dot{u}$ is the rate of specific internal energy, T is the the absolute temperature and $\dot{s}$ is the entropy production. The second principle of thermodynamics states that $\dot{s}\ge \dot{q}/T$, being $\dot{q}$ the rate of change of specific thermal energy, or simply the rate of thermal energy exchange. It is to be emphasized that:

• The rate of change of specific internal energy is related to the rate of the specific mechanical work done on the system and on the thermal energy exchange, then $\dot{u}=\dot{w}_{ext}+\dot{q}$.

• Introducing the entropy production rate due to irreversible transformations labeled as $\dot{s}^{(i)}\ge 0$, that is related to the dissipated energy, the second principle of thermodynamics can be written as $\dot{s}=\dot{q}/T+\dot{s}^{(i)}$.

By performing these two substitutions in Eq. (39) we get:

$$\begin{aligned} \dot{\psi }=\dot{w}_{ext}+\dot{q}-T\left( \dot{q}/T+\dot{s}^{(i)} \right) =\dot{w}_{ext}-D(t) \end{aligned}$$

(40)

Fig. 8

Dissipation rates for the applied strain of Fig. 7 evaluated with Eq. (43b): sinusoidal (a) and constant with initial linear ramp (b)

Fig. 9

Free energy for the applied strain of Fig. 7 evaluated with Eq. (43a): sinusoidal (a) and constant with initial linear ramp (b)

where $D(t)=T\dot{s}$ denotes the dissipation rate. When we apply a strain or stress history to the viscoelastic solid, in Eq. (40) the external work rate is known and can be evaluated as $\dot{w}_{ext}=\sigma (t) \dot{\varepsilon }(t)$. If it is possible to define also the free energy rate then also the dissipation rate can be evaluated from Eq. (40). Unfortunately the free energy is not uniquely defined unless a rheological model with well defined and distinct elastic and viscous phases is available, as it is in classical viscoelasticity. In fractional viscoelasticity the only possibility to distinguish between elastic and viscous phases is to make use of hierarchical models [11, 29, 30] but the number of elements to be taken into account is significant and depends also on the observation time and on the input on the system; for these reasons this strategy is not applicable. However, in the paper [36] the mechanical models of fractional viscoelasticity have been used to prove that the correct form of the free energy function for the fractional viscoelastic material is the one proposed by Stavermann and Schwartzl [37] and defined as:

$$\begin{aligned} \psi _{SS}=\frac{1}{2}\int _{-\infty }^t \int _{-\infty }^t R(2t-\tau _1-\tau _2)\varepsilon '(\tau _1) \varepsilon '(\tau _2)d\tau _1 d\tau _2 \end{aligned}$$

(41)

where $R(\cdot )$ is the relaxation function as usual and the pedex SS stands for Stavermann and Schwartzl. By using Eq.  (41) in Eq. (40), the following expression for the dissipation rate is obtained:

$$\begin{aligned} D(t)=-\frac{1}{2}\int _{-\infty }^t \int _{-\infty }^t \dot{R}(2t-\tau _1-\tau _2)\varepsilon '(\tau _1)\varepsilon '(\tau _2)d\tau _1 d\tau _2 \end{aligned}$$

(42)

For the particular case of the springpot Eqs. (41) and (42) read as follow:

$$\begin{aligned} \psi _{SS}= & {} \frac{C_\alpha }{2 \Gamma (1-\alpha )}\int _{-\infty }^t \int _{-\infty }^t (2t-\tau _1-\tau _2)^{-\alpha } \varepsilon '(\tau _1) \varepsilon '(\tau _2)d\tau _1 d\tau _2 \end{aligned}$$

(43a)

$$\begin{aligned} D(t)= & {} \frac{C_\alpha \alpha }{ \Gamma (1-\alpha )}\int _{-\infty }^t \int _{-\infty }^t (2t-\tau _1-\tau _2)^{-\alpha -1}\varepsilon '(\tau _1)\varepsilon '(\tau _2)d\tau _1 d\tau _2 \end{aligned}$$

(43b)

Equations (43) should be firstly applied to the one-dimensional springpot model and then to the three-dimensional springpot model; however from a one-dimensional point of view the thermodynamic consistency of the springpot has been already proved. In this case in order to evaluate the free energy and the dissipation rate it is needed to take all the components of stress and strain into account from both the volumetric and deviatoric contributions. Limitations on the relationship between $\alpha$ and $\beta$ can be found by enforcing the condition that $\psi (t)\ge 0\;\;\forall t$ and $D(t)\ge 0\;\;\forall t$. However the analytical solution of the double integrals in Eqs. (43) is not straightforward hence numerical integration has been performed. The analysis is performed for two cases: i) a sinusoidal hystory of strain is applied, but differently from the paper [31], also transient conditions are examined; ii) a constant strain, reached with a linear ramp, is applied.

Equations (43) have been evaluated by considering a large range of values of $\alpha$ and $\beta$; the other mechanical parameters ($G_\alpha$ and $K_\beta$) are chosen positive, because negative value of multiplicative parameters violate thermodynamic restrictions also in one-dimensional conditions. For simplicity here we show only results with the following values: (1) $\alpha =\beta =0.5$; (2) $\alpha =0.5$, $\beta =0.25$; (3) $\alpha =0.5$, $\beta =0.75$. Figure 8 shows the specific dissipation rate (dissipation rate per unit volume), while Fig. 9 show s the specific free energy function for the two applied strain histories of Fig. 7.

Figures 8 and 9 show that the dissipation rate and the free energy function are non-negative whatever the relationship between the values of $\alpha$ and $\beta$ is. From this evidence it has to be concluded that the 3D fractional viscoelastic models are thermodynamically consistent independently of the relationship between $\alpha$ and $\beta$; this means that both an increasing and a decreasing viscoelastic Poisson’s ratio are possible for 3D fractional constitutive models that hence are suitable to represent both behaviors.