Narrow Escape, Part III: Non-Smooth Domains and Riemann Surfaces

Abstract

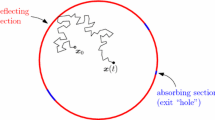
We consider the narrow escape problem in two-dimensional Riemannian manifolds (with a metric g) with corners and cusps, in an annulus, and on a sphere. Specifically, we calculate the mean time it takes a Brownian particle diffusing in a domain Ω to reach an absorbing window when the ratio ${\varepsilon= {\frac{|\partial \Omega_a|_g}{|\partial \Omega|_g}}}$ between the absorbing window and the otherwise reflecting boundary is small. If the boundary is smooth, as in the cases of the annulus and the sphere, the leading term in the expansion is the same as that given in part I of the present series of papers, however, when it is not smooth, the leading order term is different. If the absorbing window is located at a corner of angle α, then $E\tau = { \frac{|\Omega|_g}{\alpha D}}[\log{\frac{1}{\varepsilon}}+O(1)],$ if near a cusp, then $E\tau$ grows algebraically, rather than logarithmically. Thus, in the domain bounded between two tangent circles, the expected lifetime is $E\tau ={\frac{|\Omega|}{(d^{-1}-1)D}}(\frac{1}{\varepsilon} +O(1))$, where $d<1$ is the ratio of the radii. For the smooth boundary case, we calculate the next term of the expansion for the annulus and the sphere. It can also be evaluated for domains that can be mapped conformally onto an annulus. This term is needed in real life applications, such as trafficking of receptors on neuronal spines, because $\log{\frac{1}{\varepsilon}}$ is not necessarily large, even when $\varepsilon = {\frac{|\partial \Omega_a|_g}{|\partial \Omega|_g}}$ is small. In these two problems there are additional parameters that can be small, such as the ratio δ of the radii of the annulus. The contributions of these parameters to the expansion of the mean escape time are also logarithmic. In the case of the annulus the mean escape time is $E\tau = {\frac{|\Omega|_g}{\pi D} [\log\frac{1}{\varepsilon}+\frac 12\log\frac{1}{\delta}+O(1)]}$.