Single machine scheduling problems with uncertain parameters and the OWA criterion

Abstract

In this paper a class of single machine scheduling problems is discussed. It is assumed that job parameters, such as processing times, due dates, or weights are uncertain and their values are specified in the form of a discrete scenario set. The ordered weighted averaging (OWA) aggregation operator is used to choose an optimal schedule. The OWA operator generalizes traditional criteria used in decision making under uncertainty, such as the maximum, average, median, or Hurwicz criterion. It also allows us to extend the robust approach to scheduling by taking into account various attitudes of decision makers towards a risk. In this paper, a general framework for solving single machine scheduling problems with the OWA criterion is proposed and some positive and negative computational results for two basic single machine scheduling problems are provided.

1 Introduction

Scheduling under uncertainty is an important and extensively studied area of operations research and discrete optimization. The importance of this research direction results from the fact that in many real-world problems the precise values of parameters in scheduling models are not known in advance. Thus, instead of possessing the exact values of the parameters, decision makers have rather a set of all their possible realizations, called a scenario set. In some cases, an additional information with this scenario set is available. If a probability distribution in the scenario set is known, then stochastic approach can be used, which typically consists in minimizing the expected solution cost (see, e.g., Pinedo 2002). The unknown probability distribution can be upper bounded by a possibility distribution, which leads to possibilistic (fuzzy) scheduling problems (see, e.g., Kasperski and Zieliński 2011). Finally, if no additional information with scenario set is provided, then robust approach is usually used (see, e.g., Kouvelis and Yu 1997). In the robust optimization, we seek a solution minimizing a cost in a worst case, which usually leads to applying the min-max or min-max regret criterion for choosing a solution.

The robust approach to decision making is often regarded as too conservative or pessimistic. It follows from the fact, that the min-max criterion takes only the worst-case scenarios into account, ignoring the information connected with the remaining scenarios. This criterion also assumes that decision makers are very risk averse, which is not always true. These drawbacks of the min-max criterion are well known in decision theory, and a detailed discussion on this topic can be found, for example, in Luce and Raiffa (1957). In this paper, we will assume that a scenario set associated with scheduling problem is specified by enumerating all possible scenarios. Such a representation of scenario sets is called a discrete uncertainty representation and has been described, for instance, in Kouvelis and Yu (1997). Our goal is to generalize the min-max approach to scheduling problems under uncertainty by using the Ordered Weighted Averaging aggregation operator (OWA for short) introduced by Yager (1988). The OWA operator is widely applied to aggregate criteria in multiobjective decision problems (see, e.g., Galand and Spanjaard 2012; Kacprzyk et al. 2011; Ogryczak and Śliwiński 2003) but it can also be applied to choose a solution under the discrete uncertainty representation by identifying scenarios with objectives in a natural way. The OWA operator generalizes the classical criteria used in decision making under uncertainty such as the maximum, minimum, average, median, or Hurwicz criterion (a description of these criteria can be found, for example, in Luce and Raiffa 1957). So, by using OWA we can extend the min-max approach, typically used in the robust optimization. Furthermore, the weights used in the OWA operator allow us to model various attitudes of decision makers towards a risk.

Since we generalize the min-max approach to single machine scheduling problems under the discrete uncertainty representation, let us briefly recall the known results in this area (see also Kasperski and Zieliński 2014 for a survey). The min-max version of the single machine scheduling problem with the total flow time criterion has been studied in Yang and Yu (2002), where it has been shown that the problem is NP-hard even for two processing time scenarios and strongly NP-hard when the number of processing time scenarios is a part of the input (the unbounded case). A generalization of this problem, with the weighted sum of completion times criterion, has been recently discussed in Mastrolilli et al. (2013) and Regis de Farias et al. (2010) where, in particular, several inapproximability results for that problem have been established. We will describe these results in more detail later in this paper. In Aloulou and Croce (2008) the min-max version of the single machine scheduling problem with the maximum weighted tardiness criterion has been discussed, where it has been shown that some special cases of the problem are polynomially solvable. In this paper, we generalize and extend the algorithms proposed in Aloulou and Croce (2008). In Aissi et al. (2011) and Aloulou and Croce (2008) the min-max version of the single machine scheduling problem with the number of late jobs criterion has been investigated. It has been shown in Aloulou and Croce (2008) that the problem is NP-hard for deterministic due dates and two processing time scenarios. On the other hand, it has been shown in Aissi et al. (2011) that the problem with unit processing times and the number of due date scenarios being a part of the input is strongly NP-hard and hard to approximate within a factor less than 2. In a more general version of this problem the weighted sum of late jobs is minimized. This problem is known to be NP-hard for two weight scenarios (Averbakh 2001), strongly NP-hard and hard to approximate within any constant factor if the number of weight scenarios is a part of the input (Kasperski et al. 2013).

This paper is organized as follows. Section 2 presents a formulation of the general problem under consideration as well as some of its special cases. Section 3 provides an interpretation of the OWA operator and the resulting scheduling problems with uncertain parameters. The next two sections discuss two basic single machine scheduling problems. Namely, Sect. 4 explores the problem with the maximum weighted tardiness cost function and Sect. 5 investigates the problem in which the cost function is the weighted sum of completion times. We show that both problems have various computational properties which depend on the weight distribution in the OWA operator. For some weight distributions the problems are polynomially solvable, while for other ones they become strongly NP-hard and are also hard to approximate.

2 Problem formulation

Let $J=\{J_1,\dots ,J_n\}$ be a set of jobs which must be processed on a single machine. For simplicity of notations, we will identify job $J_j$ with its index j. The set of jobs may be partially ordered by some precedence constraints. The notation $i\rightarrow j$ means that processing of job j cannot start before processing of job i is completed (job j is called a successor of job i). For each job j the following parameters may be specified: a nonnegative processing time $p_j$, a nonnegative due date $d_j$, and a nonnegative weight $w_j$. The due date $d_j$ expresses a desired completion time of j and the weight $w_j$ expresses the importance of job j relative to the other jobs in the system. In all scheduling models discussed in this paper, we assume that all the jobs are ready for processing at time 0, in other words, each job has a release date equal to 0. We also assume that each job must be processed without any interruptions, so we consider only nonpreemptive models. Under these assumptions we can define a schedule $\pi$ as a feasible permutation of the jobs, in which the precedence constraints among the jobs are preserved. The set of all feasible schedules will be denoted by $\Pi$.

Let us denote by $C_j(\pi )$ the completion time of job j in schedule $\pi$. We will use $f(\pi )$ to denote a cost of schedule $\pi$. The value of $f(\pi )$ depends on job completion times and may also depend on job due dates or weights. In this paper, we will investigate two basic scheduling problems, in which the cost function is the maximum weighted tardiness, i.e., $f(\pi )=\max _{j\in J} w_j[C_j(\pi )-d_j]^+$ (we use the notation $[x]^+=\max \{0,x\}$) and the weighted sum of completion times, i.e., $f(\pi )=\sum _{j\in J} w_j C_j(\pi )$. In the deterministic case, we wish to find a feasible schedule which minimizes the cost $f(\pi )$, that is:

$$\begin{aligned} \mathcal {P}:\; \min _{\pi \in \Pi } f(\pi ). \end{aligned}$$

We now study a situation in which some or all problem parameters are ill-known. Let S be a vector of the problem parameters which may occur. The vector S is called a scenario. We will use $p_j(S)$, $d_j(S)$, and $w_j(S)$ to denote the processing time, due date, and weight of job j under scenario S. A parameter is deterministic (precisely known) if its value is the same under each scenario. Let a scenario set $\Gamma =\{S_1,\dots ,S_K\}$ contain all possible scenarios, where $K> 1$. In this paper, we distinguish the bounded case, where K is bounded by a constant and the unbounded case, where K is a part of the input. Now, the completion time of job j in $\pi$ and the cost of $\pi$ depend on scenario $S_i \in \Gamma$ and will be denoted by $C_j(\pi ,S_i)$ and $f(\pi ,S_i)$, respectively.

Since scenario set $\Gamma$ contains more than one scenario, an additional criterion is required to choose a reasonable solution. In this paper, we suggest to use the Ordered Weighted Averaging aggregation operator (OWA for short) proposed by Yager (1988). We now describe this criterion. Let $(f_1,\ldots ,f_K)$ be a vector of real numbers. Let us introduce a vector of weights $\pmb {v}=(v_1,\ldots ,v_K)$ such that $v_j\in [0,1]$ for all $j\in [K]$ ([K] stands for the set $\{1,\dots ,K\}$) and $v_1+\cdots +v_K=1$. Let $\sigma$ be a permutation of [K] such that $f_{\sigma (1)}\ge f_{\sigma (2)}\ge \cdots \ge f_{\sigma (K)}$. The OWA operator is defined as follows:

$$\begin{aligned} \mathrm{owa}_{\pmb {v}}(f_1,\ldots ,f_K)=\sum _{i\in [K]} v_i f_{\sigma (i)}. \end{aligned}$$

The OWA operator has several natural properties which follow directly from its definition (see, e.g., Kacprzyk et al. 2011). Since it is a convex combination of the cost functions, $\min (f_1,\ldots ,f_K) \le \mathrm {owa}_{\pmb {v}}(f_1,\ldots ,f_K) \le \max (f_1,\ldots ,f_K)$. It is also monotonic, i.e., if $f_j \ge g_j$ for all $j\in [K]$, then $\mathrm {owa}_{\pmb {v}}(f_1,\ldots ,f_K)\ge \mathrm {owa}_{\pmb {v}}(g_1,\ldots ,g_K)$, idempotent, i.e., if $f_1\!=\!\cdots \!=\!f_k=a$, then $\mathrm {owa}_{\pmb {v}}(f_1,\ldots ,f_K)=a$ and symmetric, i.e. its value does not depend on the order of the values $f_j$, $j\in [K]$. The OWA operator generalizes some important criteria used in decision making under uncertainty and we will discuss this fact in detail in Sect. 3. We now use the OWA operator to aggregate the costs of a given schedule $\pi$ under scenarios in  $\Gamma$. Let us define

$$\begin{aligned} {\mathrm {OWA}}(\pi )= & {} \mathrm{owa}_{\pmb {v}}(f(\pi ,S_1),\ldots ,f(\pi ,S_K))\\= & {} \sum _{i\in [K]} v_i f(\pi ,S_{\sigma (i)}), \end{aligned}$$

where $\sigma$ is a permutation of [K] such that $f(\pi ,S_{\sigma (1)})\ge \dots \ge f(\pi ,S_{\sigma (K)})$. In this paper, we examine the following optimization problem:

$$\begin{aligned} {\textsc {Min-Owa}}~\mathcal {P}: \min _{\pi \in \Pi } {\mathrm {OWA}} (\pi ). \end{aligned}$$

3 Interpretation of the problem

In this section, we discuss in detail an interpretation of the Min-Owa $\mathcal {P}$ problem. We also compare the proposed approach with the traditional min-max (regret) approach used in robust discrete optimization (Kouvelis and Yu 1997). Notice first, that the OWA operator generalizes some classical criteria used in decision making under uncertainty. If $v_1=1$ and $v_j=0$ for $j=2,\ldots ,K$, then OWA becomes the maximum. If $v_K=1$ and $v_j=0$ for $j=1,\ldots ,K-1$, then OWA becomes the minimum. In general, if $v_k=1$ and $v_j=0$ for $j\in [K]{\setminus }\{k\}$, then OWA is the kth largest element among $f_1,\ldots ,f_K$. In particular, when $k=\lfloor K/2 \rfloor +1$, the kth element is the median. If $v_j=1/K$ for all $j\in [K]$, i.e., when the weights are uniform, then OWA is the average (or the Laplace criterion). Finally, if $v_1=\alpha$ and $v_K=1-\alpha$ for some fixed $\alpha \in [0,1]$ and $v_j=0$ for the remaining weights, then we get the Hurwicz pessimism-optimism criterion. Hence Min-Owa $\mathcal {P}$ contains the problems listed in Table 1 as special cases.

Table 1 Special cases of Min-Owa $\mathcal {P}$

The Min-Owa $\mathcal {P}$ problem can be consistent with the concept of robustness. Namely, risk averse decision makers should choose nonincreasing weights, i.e., such that $v_1\ge v_2\ge \dots \ge v_K$. We can now consider two extreme cases of nonincreasing weights. When $v_1=1$, then we get the maximum criterion traditionally used in robust optimization. On the other hand, when $v_1=1/K$, then we get the average (the Laplace criterion), which can be seen as the expected solution cost with respect to the uniform probability distribution over scenarios. Hence the nonincreasing weights allow us to establish a trade-off between the very conservative maximum criterion and the average criterion.

Table 1 contains the basic criteria used in decision making under uncertainty, except for the min-max regret (also called the Savage criterion). The regret of a given schedule $\pi$ under scenario S is the difference between the cost of $\pi$ under S and the cost of an optimal schedule under S. It thus expresses an opportunity loss for $\pi$ under S. In the Min-Max Regret $\mathcal {P}$ problem we seek a schedule minimizing the maximum regret over all scenarios. It has interesting computational properties for the interval uncertainty representation, i.e., when for each job parameter an interval of its possible values is specified (see, e.g., Lebedev and Averbakh 2006; Kasperski 2005; Kouvelis and Yu 1997). In the traditional robust approach we apply the min-max and min-max regret criteria to choose a solution (Kouvelis and Yu 1997). In order to illustrate some drawbacks of the min-max (regret) approach, consider the problem $1||\sum C_j$ for three jobs and two processing time scenarios, shown in Table 2.

Table 2 Two processing times scenario sets for three jobs

If the min-max criterion is applied to the scenario set from Table 2a, then we may get any schedule. This happens, because the job processing times under $S_1$ are equal and large enough in comparison with $S_2$. In particular, we may get schedule $\pi =(3,2,1)$ which is even not Pareto optimal and, clearly, is not a good choice. We get a better solution after using the OWA criterion with positive weights $v_1$ and $v_2$. Notice that when all weights in the OWA criterion are positive, then OWA is a strict convex combination of the schedule costs, and the resulting optimum schedule must be Pareto optimal. Since the regret of any schedule under $S_1$ is 0, we also get a better solution after applying the min-max regret criterion. However, using the min-max regret criterion may be also questionable. Indeed, consider the scenario set shown in Table 2b. Schedule $\pi _1=(2,1,3)$ has the smallest maximum regret equal to 8. However, its maximum cost is equal to 54, while the maximum cost of schedule $\pi _2=(2,3,1)$ is only 48 (the maximum regret of $\pi _2$ is equal to 16). This simple example demonstrates that in the min-max and min-max regret approaches we minimize quite different quantities. Using the min-max criterion our aim is to find a cheapest schedule, while using the min-max regret one we wish to minimize the opportunity loss, rather than the cost. In this paper, by using the OWA operator, we generalize the first goal, i.e. we assume that decision makers are interested in minimizing the schedule cost rather than the regret. Then, the weights in the OWA operator allow us to take the attitude of decision maker towards the risk, where by risk we mean a possibility that a schedule computed will have a large cost (not regret) under some scenario. This leads to the classical criteria used in decision making under uncertainty, except for the maximum regret one. An excellent and deep discussion on the properties of various criteria used in decision making under uncertainty, including the maximum regret criterion, can be found in Luce and Raiffa (1957).

Yet another drawback of applying the min-max (regret) approach in some situations is that only one scenario, i.e., a worst-case scenario, is taken into account while evaluating a schedule. For instance, if we add new scenarios to the sample scenario sets from Table 2, under which the schedules have small costs (regrets), then these scenarios will be ignored while computing a solution. This phenomenon is called the drowning effect (Dubois and Fortemps 1999). Hence, a criterion that takes into account all, or at least a subset of scenarios in a process of choosing a solution may be appropriate. It is easy to see that this requirement is satisfied by the OWA criterion.

As we will see in the next sections, the complexity of Min-Owa $\mathcal {P}$ depends on the properties of the underlying deterministic problem $\mathcal {P}$ and the weights $v_1,\dots , v_K$. One general and easy observation can be made. Namely, if $\mathcal {P}$ is solvable in T(n) time, then Min-Min $\mathcal {P}$ is solvable in $O(K\cdot T(n))$ time. Indeed, in order to solve the Min-Min $\mathcal {P}$ problem it is enough to compute an optimal schedule $\pi _k$ under each scenario $S_k$, $k\in [K]$, and choose the one which has the minimum value of $f(\pi _k, S_k)$, $k\in [K]$. For the remaining problems listed in Table 1 no such general result can be established and their complexity depends on a structure of the deterministic problem $\mathcal {P}$.

4 The maximum weighted tardiness cost function

Let $T_j(\pi ,S_i)=[C_j(\pi ,S_i)-d_j(S_i)]^+$ be the tardiness of job j in $\pi$ under scenario $S_i$, $i\in [K]$. The cost of schedule $\pi$ under $S_i$ is the maximum weighted tardiness under $S_i$, i.e., $f(\pi ,S_i)=\max _{j\in J} w_j(S_i) T_j(\pi ,S_i)$. The underlying deterministic problem $\mathcal {P}$ is denoted by $1|prec|\max w_jT_j$ in Graham’s notation (Graham et al. 1979). In this section, we will also discuss a special case of this problem, denoted by $1||T_{\max }$, with unit job weights under all scenarios and no precedence constraints between the jobs. The deterministic $1|prec|\max w_j T_j$ problem can be solved in $O(n^2)$ time by the well-known algorithm designed by Lawler (1973). It follows directly from the Lawler’s algorithm that $1||T_{\max }$ can be solved in $O(n\log n)$ time by applying the EDD rule, i.e., by ordering the jobs with respect to nondecreasing due dates.

This section contains the following results. We will consider first the case when K is unbounded (K is a part of the input). We will show that the problems of minimizing the average cost or median of the costs are then strongly NP-hard and also hard to approximate. On the other hand, we will prove that the problems of minimizing the maximum cost or the Hurwicz criterion are solvable in polynomial time. We will consider next the problem with a constant K. It turns out that in this case the general problem of minimizing the OWA criterion can be solved in pseudopolynomial time. Finally, we will propose an approximation algorithm, which can be efficiently applied to some particular weight distributions in the OWA criterion.

4.1 Hardness of the problem

The following theorem characterizes the complexity of the problem:

Theorem 1

If the number of scenarios is unbounded, then

• (i) Min-Average $1||T_{\max }$ is strongly NP-hard and not approximable within $7/6-\epsilon$ for any $\epsilon >0$ unless P=NP,

• (ii) Min-Median $1|| T_{\max }$ is strongly NP-hard and not at all approximable unless P=NP.

Furthermore, both assertions remain true even for jobs with unit processing times under all scenarios.

Proof

We show a polynomial time approximation-preserving reduction from the Min k-Sat problem, which is defined as follows. We are given boolean variables $x_1,\ldots ,x_n$ and a collection of clauses $C_1,\ldots , C_m$, where each clause is a disjunction of at most k literals (variables or their negations). We ask if there is an assignment to the variables which satisfies at most $L<m$ clauses. This problem is strongly NP-hard even for $k=2$ (see Avidor and Zwick 2002; Kohli et al. 1994; Marathe and Ravi 1996) and its optimization (minimization) version is hard to approximate within $7/6-\epsilon$ for any $\epsilon >0$ when $k=3$ (see Avidor and Zwick 2002).

We first consider assertion (i). Given an instance of Min 3-Sat, we construct the corresponding instance of Min-Average $1||T_{\max }$ in the following way. We create two jobs $J_{x_i}$ and $J_{\overline{x}_i}$ for each variable $x_i$, $i\in [n]$. The processing times and weights of all the jobs under all scenarios are equal to 1. The due dates of $J_{x_i}$ and $J_{\overline{x}_i}$ depend on scenario and will take the value of either $2i-1$ or 2i. Set $K=m$ and form K scenario set $\Gamma$ in the following way. Scenario $S_k$ corresponds to clause $C_k=(l_1 \vee l_2 \vee l_3)$. For each $q=1,2,3$, if $l_q=x_i$, then the due date of $J_{x_i}$ is $2i-1$ and the due date of $J_{\overline{x}_i}$ is 2i; if $l_q=\overline{x}_i$, then the due date of $J_{x_i}$ is 2i and the due date of $J_{\overline{x}_i}$ is $2i-1$; if neither $x_i$ nor $\overline{x}_i$ appears in $C_k$, then the due dates of $J_{x_i}$ and $J_{\overline{x}_i}$ are set to 2i. A sample reduction is shown in Table 3. Finally, we fix $v_k=1/m$ for all $k\in [K]$. Let us define a subset of the schedules $\Pi '\subseteq \Pi$ such that each schedule $\pi \in \Pi '$ is of the form $\pi =(J_1,J_1',J_2,J_2',\ldots ,J_n,J_n')$, where $J_i,J_i'\in \{J_{x_i},J_{\overline{x}_i}\}$ for $i\in [n]$. Observe that $\Pi '$ contains exactly $2^n$ schedules and each such a schedule defines an assignment to the variables such that $x_i=0$ if $J_{x_i}$ is processed before $J_{\overline{x}_i}$ and $x_i=1$ otherwise. Assume that the answer to Min 3-Sat is yes. So, there is an assignment to the variables which satisfies at most L clauses. Choose schedule $\pi \in \Pi '$ which corresponds to this assignment. It is easily seen that if clause $C_k$ is not satisfied, then all jobs in $\pi$ under $S_k$ are on-time and the maximum tardiness in $\pi$ under $S_k$ is 0. On the other hand, if clause $C_k$ is satisfied, then the maximum tardiness of $\pi$ under $S_k$ is 1. In consequence $\frac{1}{K}\sum _{k \in [K]} f(\pi ,S_k)\le L/m$. Assume now that there is a schedule $\pi$ such that $\frac{1}{K}\sum _{k \in [K]} f(\pi ,S_k)\le L/m$. Notice that $L/m < 1$ by the nonrestrictive assumption that $L<m$. We first show that $\pi$ must belong to $\Pi '$. Suppose that $\pi \notin \Pi '$ and let $J_i$ ($J_i')$ be the last job in $\pi$ which is not placed properly, i.e., $J_i,(J_i')\notin \{J_{x_i},J_{\overline{x}_i}\}$. Then $J_i$ ($J_i'$) is at least one unit late under all scenarios and $\frac{1}{K}\sum _{k \in [K]} f(\pi ,S_k)\ge 1$, a contradiction. Since $\pi \in \Pi '$ and all processing times are equal to 1 it follows that $f(\pi ,S_k)\in \{0,1\}$ for all $k\in [K]$. Consequently, the maximum tardiness in $\pi$ is equal to 1 under at most L scenarios and the assignment corresponding to $\pi$ satisfies at most L clauses. The above reduction is approximation-preserving and the inapproximability result immediately holds.

Table 3 The due date scenarios for the formula $(x_1\vee \overline{x}_2 \vee \overline{x}_3)\wedge (\overline{x}_2 \vee \overline{x}_3 \vee x_4) \wedge (\overline{x}_1 \vee x_2 \vee \overline{x}_4) \wedge (x_1 \vee x_2 \vee x_3) \wedge (x_1 \vee x_3 \vee \overline{x}_4)$

In order to prove assertion (ii), it suffices to modify the previous reduction. Assume first that $L<\lfloor m/2 \rfloor$. We then add to scenario set $\Gamma$ additional $m-2L$ scenarios with the due dates equal to 0 for all the jobs. So the number of scenarios K is $2m-2L$. We fix $v_{m-L+1}=1$ and $v_k=0$ for the remaining scenarios. Now, the answer to Min 3-Sat is yes, if and only if there is a schedule $\pi$ whose maximum tardiness is positive under at most $L+m-2L=m-L$ scenarios. According to the definition of the weights ${\mathrm {OWA}}(\pi )=0$. Assume that $L>\lfloor m/2 \rfloor$. We then add to $\Gamma$ additional $2L-m$ scenarios with the due dates to n for all the jobs. The number of scenarios K is then 2L. We fix $v_{L+1}=1$ and $v_k=0$ for all the remaining scenarios. Now, the answer to Min 3-Sat is yes, if and only if there is a schedule $\pi$ whose cost is positive under at most L scenarios. According to the definition of the weights ${\mathrm {OWA}}(\pi )=0$. We thus can see that it is NP-hard to check whether there is a schedule $\pi$ such that $\mathrm{OWA}(\pi )\le 0$ and the theorem follows. $\square$

The next theorem characterizes the problem complexity when job processing times and due dates are deterministic and only job weights are uncertain.

Theorem 2

If the number of scenarios is unbounded, then

• (i) Min-Average $1||\max w_j T_j$ is strongly NP-hard.

• (ii) Min-Median $1||\max w_j T_j$ is strongly NP-hard and not at all approximable unless P=NP.

Furthermore, both assertions are true when all jobs have unit processing times under all scenarios and all job due dates are deterministic.

Proof

As in the proof of Theorem 1, we show a polynomial time reduction from the Min 3-Sat problem. We start by proving assertion (i). We create two jobs $J_{x_i}$ and $J_{\overline{x}_i}$ for each variable $x_i$. The processing times of these jobs under all scenarios are 1 and their due dates are equal to $2i-1$. Now for each clause $C_k=(l_1 \vee l_2 \vee l_3)$ we form the weight scenario $S_k$ as follows: for each $q=1,2,3$, if $l_q=x_i$, then the weight of $J_{x_i}$ is 1 and the weight of $J_{\overline{x}_i}$ is 0; if $l_q=\overline{x}_i$, then the weight of $J_{\overline{x}_i}$ is 1 and the weight of $J_{x_i}$ is 0; if neither $x_i$ nor $\overline{x}_i$ appears in $C_k$, then the weights of $J_{x_i}$ and $J_{\overline{x}_i}$ are 0. We also add one additional scenario $S_{m+1}$ under which the weight of each job is equal to m. We set $K=m+1$ and fix $v_k=1/(m+1)$ for each $k\in [K]$. We define the subset of schedules $\Pi '\subseteq \Pi$ as in the proof of Theorem 1.

We will show that the answer to Min 3-Sat is yes if and only if there is a schedule $\pi$ such that $\mathrm{OWA}(\pi )\le (m+L)/(m+1)$. Assume that the answer to Min 3-Sat is yes. Let $\pi \in \Pi '$ be the schedule corresponding to the assignment which satisfies at most L clauses (see the proof of Theorem 1). It is easy to verify that $f(\pi ,S_k)=0$ if $C_k$ is not satisfied and $f(\pi ,S_k)=1$ if $C_k$ is satisfied. Furthermore, $f(\pi ,S_{m+1})=m$. Hence $\mathrm{OWA}(\pi )\le (m+L)/(m+1)$. Assume now that $\mathrm{OWA}(\pi )\le (m+L)/(m+1)$. Then $\pi$ must belong to $\Pi '$ since otherwise $f(\pi , S_{m+1})\ge 2m$ and $\mathrm{OWA}(\pi )\ge 2m/(m+1)$, which contradicts the assumption that $L<m$. It must hold $f(\pi , S_{m+1})=m$ and $f(\pi , S_i)\in \{0,1\}$ for each $i\in [K]$. Consequently $f(\pi ,S_i)=1$ under at most L scenarios, which means that the assignment corresponding to $\pi$ satisfies at most L clauses and the answer to Min 3-Sat is yes.

The proof of assertion (ii) is very similar to the corresponding proof in Theorem 1. $\square$

4.2 Polynomially and pseudopolynomially solvable cases

In this section, we identify some special cases of the Min-Owa $1|prec|\max w_j T_j$ problem which are polynomially or pseudopolynomially solvable.

4.2.1 The maximum criterion

It has been shown in Aloulou and Croce (2008) that Min-Max $1|prec|T_{\max }$ is solvable in $O(Kn^2)$ time. In this section, we will show that more general version of the problem with arbitrary nonnegative job weights, Min-Max $1|prec|\max w_j T_j$, is solvable in $O(Kn^2)$ time as well. In the construction of the algorithm, we will use some ideas from Kasperski (2005) and Volgenant and Duin (2010). Furthermore, the algorithm with some minor modifications will be a basis for solving other special cases of Min-Owa $1|prec|\max w_j T_j$. In this section the OWA operator is the maximum, so $\mathrm{OWA}(\pi )=\max _{i\in [K]} f(\pi ,S_i)$. By interchanging the maximum operators and some easy transformations, we can express the value of ${\mathrm {OWA}}(\pi )$ as follows:

$$\begin{aligned} {\mathrm {OWA}}(\pi ) = \max _{j\in J}\max _{i\in [K]} \big [w_j(S_i)(C_j(\pi ,S_i)-d_j(S_i))\big ]^+. \end{aligned}$$

(1)

Fix a nonempty subset of jobs $D\subseteq J$ and define

$$\begin{aligned} F_j(D)=\max _{i\in [K]} \left[ w_j(S_i) \left( \sum _{k\in D} p_k(S_i)-d_j(S_i)\right) \right] ^+. \end{aligned}$$

(2)

The following proposition immediately follows from the fact that all job processing times and weights are nonnegative:

Proposition 1

If $D_2\subseteq D_1$, then for any $j\in J$ it holds $F_j(D_1)\ge F_j(D_2)$.

Let $pred(\pi ,j)$ be the set of jobs containing job j and all the jobs that precede j in $\pi$. Since $C_j(\pi ,S_i)=\sum _{k\in pred(\pi ,j)} p_k(S_i)$, the maximum cost of $\pi$ over $\Gamma$ can be expressed as follows (see 1 and 2):

$$\begin{aligned} \mathrm{OWA}(\pi )=\max _{j\in J} F_j(pred(\pi ,j)). \end{aligned}$$

(3)

Consider the algorithm shown in the form of Algorithm 1.

Theorem 3

Algorithm 1 computes an optimal schedule for Min-Max $1|prec|\max w_j T_j$ in $O(Kn^2)$ time.

Fig. 1

Illustration of the proof of Theorem 1

Proof

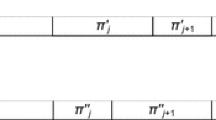
Let $\pi$ be the schedule returned by the algorithm. It is clear that $\pi$ is feasible. Let us renumber the jobs so that $\pi =(1,2,\ldots ,n)$. Let $\sigma$ be an optimal min-max schedule. Assume that $\sigma (j)=j$ for $j=k+1,\ldots ,n$, where k is the smallest position among all the optimal min-max schedules. If $k=0$, then we are done, because $\pi =\sigma$ is optimal. Assume that $k>0$, and so $k\ne \sigma (k)=i$. Let us move the job k just after i in $\sigma$ and denote the resulting schedule as $\sigma '$ (see Fig. 1). Schedule $\sigma '$ is feasible, because $\pi$ is feasible.

We need only consider three cases:

• 1. If $j \in P \cup R$, then $pred(\sigma ',j)=pred(\sigma ,j)$ and $F_j(pred(\sigma ',j))=F_j(pred(\sigma ,j))$.

• 2. If $j \in Q\cup \{i\}$, then $pred(\sigma ',j)\subseteq pred(\sigma ,j)$ and, by Proposition 1, $F_j(pred(\sigma ',j))\le F_j(pred(\sigma ,j))$.

• 3. If $j=k$, then $F_j(D)\le F_i(D)$ from the construction of Algorithm 1. Since $pred(\sigma ,i)=pred(\sigma ',j)=D$, we have $F_j(pred(\sigma ',j))\le F_i(pred(\sigma ,i))$.

From the above three cases and equality (3), we conclude that

$$\begin{aligned} \mathrm{OWA}(\sigma ')= & {} \max _{j\in J} F_j(pred(\sigma ',j))\le \max _{j\in J} F_j(pred(\sigma ,j))\nonumber \\= & {} \mathrm{OWA}(\sigma ), \end{aligned}$$

so $\sigma '$ is also optimal, which contradicts the minimality of k. Computing $F_j(D)$ for a given $j\in D$ in line 6 requires O(K) time (note that $p(S_i)$, $i\in [K]$, store the values of $\sum _{k\in D} p_k(S_i)$ that have been computed in lines 2-4 and they are updated in lines 9-11), and thus line 6 can be executed in O(Kn) time. Consequently, the overall running time of the algorithm is $O(Kn^2)$. $\square$

4.2.2 The Hurwicz criterion

In this section, we explore the problem with the Hurwicz criterion. We will examine the case in which $\alpha \in (0,1)$ as the boundary cases with $\alpha$ equal to 0 (the minimum criterion) or 1 (the maximum criterion) are solvable in $O(Kn^2)$ time.

Theorem 4

Min-Hurwicz $1|prec|\max w_j T_j$ is solvable in $O(K^2 n^4 )$ time.

Fig. 2

The functions $\Psi _3(t)$ (the dotted line) and $0.5\Psi _3(t)+0.5t$, $t\in [18,60]$ (the solid line), for a sample problem (there are no precedence constraints between the jobs). The function $H_3(\pi )$ is minimized for $\pi _2=(1,4,2,5,3)$ and $H_3(\pi _2)=51.5$

Proof

The Hurwicz criterion can be expressed as follows:

$$\begin{aligned} \text {OWA}(\pi )=\alpha \max _{i\in [K]}f(\pi ,S_i) +(1-\alpha )\min _{i\in [K]} f(\pi ,S_i). \end{aligned}$$

Let us define

$$\begin{aligned} H_k(\pi )=\alpha \max _{i\in [K]}f(\pi ,S_i) +(1-\alpha ) f(\pi ,S_k). \end{aligned}$$

Hence

$$\begin{aligned} \min _{\pi \in \Pi } \text {OWA}(\pi )=\min _{k\in [K]} \min _{\pi \in \Pi } H_k(\pi ), \end{aligned}$$

and the problem of minimizing the Hurwicz criterion reduces to solving K auxiliary problems consisting in minimizing $H_k(\pi )$ for a fixed $k\in [K]$. Let us fix $k\in [K]$ and $t\ge 0$, and define $\Pi _k(t)=\{\pi \in \Pi \,:\,f(\pi ,S_k)\le t\}\subseteq \Pi$ as the set of feasible schedules whose cost under $S_k$ is at most t. Define

$$\begin{aligned} \Psi _k(t)= \min _{\pi \in \Pi _k(t)}\max _{i\in [K]} f(\pi ,S_i).\end{aligned}$$

Hence

$$\begin{aligned} \min _{\pi \in \Pi } H_k(\pi )=\min _{t\in [\underline{t}, \overline{t}]} \alpha \Psi _k(t)+(1-\alpha ) t, \end{aligned}$$

(4)

where $\underline{t}=\min _{\pi \in \Pi } f(\pi , S_k)$ (for $t<\underline{t}$ it holds $\Pi _k(t)=\emptyset$), and $\overline{t}=\min _{\pi \in \Pi }\max _{i\in [K]} f(\pi ,S_i)$, which is due to the fact that $\max _{i\in [K]} f(\pi ,S_i)\ge f(\pi ,S_k)$. Computing the value of $\Psi _k(t)$ for a given $t\in [\underline{t}, \overline{t}]$ can be done by a slightly modified Algorithm 1. It is enough to replace line 6 of Algorithm 1 with the following line:

$$\begin{aligned}&6': \text { find }j \in D_k(t),\text { which has no successor in }D,\text { and has}\\&\quad \text { a minimum value of} F_j(D), \end{aligned}$$

where $D_k(t)=\{j\in D: [w_j(S_k)(p(S_k)-d_j(S_k))]^+\le t\}$. The proof of the correctness of the modified algorithm is almost the same as the proof of Theorem 3. It is sufficient to define a feasible schedule $\pi$ as the one satisfying the precedence constraints and the additional constraint $f(\pi ,S_k)\le t$. Hence, if the algorithm returns a feasible schedule, then it must be optimal. The algorithm fails to compute a feasible schedule when $D_k(t)=\emptyset$ in line 6’. In this case, at least one job in $D\ne \emptyset$ must be completed not earlier than $p(S_k)=\sum _{j\in D} p_j(S_k)$ and $f(\pi ,S_k)>t$ for all schedules $\pi \in \Pi$, which means that $\Pi _k(t)=\emptyset$. Clearly, the modified algorithm has the same $O(Kn^2)$ running time.

Note that $\Psi _k$ is a nonincreasing step function on $[\underline{t},\infty )$, i.e., a constant function on subintervals $[\underline{t}_1,\overline{t}_1)\cup [\underline{t}_2,\overline{t}_2)\cup \cdots \cup [\underline{t}_l,\infty )$, $\overline{t}_{v-1}=\underline{t}_v$, $v=2,\ldots ,l$, $\underline{t}_1=\underline{t}$. Thus, $\alpha \Psi _k(t)+(1-\alpha ) t$, $\alpha \in (0,1)$, is a piecewise linear function on $[\underline{t},\infty )$, a linear increasing function on each subinterval $[\underline{t}_v,\overline{t}_v)$, $v\in [l]$, and attains minimum at one of the points $\underline{t}_1,\ldots , \underline{t}_l$. The functions $\Psi _k(t)$ and $\alpha \Psi _k(t)+(1-\alpha )t$ for $k=3$ are depicted in the example shown in Fig. 2. We have $\underline{t}_1=18$, $\underline{t}_2=26$, $\underline{t}_3=60$ and the function $\alpha \Psi _3(t)+(1-\alpha )t$ is minimized for $t=26$. Since $\pi _2=(1,4,2,5,3)$ is an optimal solution to $\Psi _3(26)$, we conclude that $\pi _2$ minimizes $H_3(\pi )$.

Observe that the value of t minimizing $\alpha \Psi _k(t) + (1-\alpha ) t$ can be found in pseudopolynomial time by trying all integers in the interval $[\underline{t},\overline{t}]$. We now show how to find the optimal value of t in polynomial time. We first compute $\underline{t}_1=\min _{\pi \in \Pi } f(\pi ,S_k)$, and the value of $\Psi _k(\underline{t}_1)$ by the modified Algorithm 1. Let us denote by $\pi _1$ the resulting optimal schedule, $\pi _1\in \Pi _k(\underline{t}_1)$. In the sample problem shown in Fig. 2, $\underline{t}_1=18$, $\pi _1=(2,4,5,3,1)$, and $\Psi _3(\underline{t}_1)=91$. Our goal now is to compute the value of $\underline{t}_2$. Choose the iteration of the modified Algorithm 1, in which the position of job j is fixed in $\pi _1$. The job j satisfies the condition stated in line 6’. We can now compute the smallest value of t, $t>\underline{t}_1$, for which job j violates this condition and must be replaced by some other job in $D_k(t)$. In order to do this it suffices to try all values $t_i=w_i(S_k)[p(S_k)-d_i(S_k)]^+$ for $i\in D{\setminus }\{j\}$ and fix $t^*_j$ as the smallest among them which violates the condition in line 6’ (if the condition holds for all $t_i$, then $t^*_j=\infty$). Repeating this procedure for each job we get the set of values $t^*_1,\dots , t^*_n$ and $\underline{t}_2$ is the smallest value among them. Consider again the sample problem presented in Fig. 2. When job 1 is placed at position 5 in $\pi _1$, it satisfies the condition in line 6’ for $t=18$. In fact, it holds $D_3(\underline{t}_1)=\{1\}$. Since $D=\{1,2,3,4,5\}$, we now try the values $t_2=91$, $t_3=26$, $t_4=126$, and $t_5=60$. The condition in line 6’ is violated for $t=t_3=26$ as $D_3(26)=\{1,3\}$ and $F_3(D)<F_1(D)$. Hence $t^*_1=26$. In the same way we compute the remaining values $t_2^*,\ldots , t^*_5$. It turns out that $t_1^*=26$ is the smallest among them, thus $\underline{t}_2=26$. The value of $\underline{t}_3$ can be found in the same way. We compute an optimal schedule $\pi _2$ corresponding to $\Psi _k(\underline{t}_2)$ and repeat the previous procedure.

Consider the sequence of schedules $\pi _l, \pi _{l-1},\ldots ,\pi _1$, where $\pi _v$ minimizes $\Psi _k(\underline{t}_v)$. Schedule $\pi _{v-1}$ can be obtained from $\pi _v$ by moving the position of at least one job in $\pi _v$, say j, whose current position becomes infeasible as t decreases, to the left. Furthermore the position of j cannot increase in all the subsequent schedules $\pi _{v-2}, \ldots , \pi _1$, because the function $f(\pi ,S_k)$ is nondecreasing (if j cannot be placed at ith position, then it also cannot be placed at positions $i+1,\ldots ,n$). Hence, if $\pi _l$ is the last schedule, then the position of job $\pi _l(i)$ can be decreased at most $i-1$ times which implies $l=O(n^2)$. Hence problem (4) can be solved in $O(Kn^4)$ time and Min-Hurwicz $1|prec|\max w_j T_j$ is solvable in $O(K^2 n^4)$ time. $\square$

4.2.3 The kth largest cost criterion

In this section, we investigate the Min-Quant( k ) $1|prec|\max w_j T_j$ problem. Thus our goal is to minimize the kth largest schedule cost. It is clear that this problem is polynomially solvable when $k=1$ or $k=K$. It is, however, strongly NP-hard and not at all approximable when k is a function of K, in particular, when the median of the costs is minimized (see Theorem 1). We now explore the case when k is constant.

Theorem 5

Min-Quant( k ) $1|prec|\max w_j T_j$ is solvable in $O\left( \left( {\begin{array}{c}K\\ k-1\end{array}}\right) (K-k+1) n^2 \right)$ time, which is polynomial when k is constant.

Proof

The algorithm works as follows. We enumerate all the subsets of scenarios of size $k-1$. For each such a subset, say C, we solve Min-Max $1|prec|\max w_j T_j$ for the scenario set $\Gamma {\setminus } C$, using Algorithm 1, obtaining a schedule $\pi _C$. Among the schedules computed we return $\pi _C$ for which the maximum cost over $\Gamma {\setminus } C$ is minimal. It is straightforward to verify that this schedule must be optimal. The number of subsets which have to be enumerated is $\left( {\begin{array}{c}K\\ k-1\end{array}}\right)$. For each such a subset we solve Min-Max $1|prec|\max w_j T_j$ with scenarios set $\Gamma {\setminus } C$, which requires $O((K-k+1) n^2)$ time and the theorem follows. $\square$

The algorithm suggested in the proof of Theorem 5 is efficient when k is close to 1 or close to K. When k is a function of K, then this running times becomes exponential and may be prohibitive in practice. In Sect. 4.3, we will use this algorithm to construct an approximation algorithm for the general Min-Owa $1|prec|\max w_j T_j$ problem.

4.2.4 The OWA criterion: the bounded case

In Sect. 4.1, we have shown that for the unbounded case Min-Owa $1|prec|\max w_j T_j$ is strongly NP-hard and not at all approximable unless P=NP. In this section, we investigate the case when K is constant. Without loss of generality we can assume that all the parameters are nonnegative integers. Let $f_{\max }$ be an upper bound on the maximum weighted tardiness of any job under any scenario. By Proposition 1 and equality (3) we can fix $f_{\max }=\max _{j\in J} F_j(J)$.

Theorem 6

Min-Owa $1|prec|\max w_j T_j$ is solvable in $O(f_{\max }^K Kn^2)$ time, which is pseudopolynomial if K is constant.

Proof

Let $\pmb {t}=(t_1,\ldots ,t_K)$ be a vector of nonnegative integers. Let $\Pi (\pmb {t})\subseteq \Pi$ be a subset of the set of feasible schedules such that $\pi \in \Pi (\pmb {t})$ if $f(\pi ,S_i)\le t_i$ for all $i\in [K]$, i.e., the maximum weighted tardiness in $\pi$ under $S_i$ does not exceed $t_i$. Consider the following auxiliary problem. Given a vector $\pmb {t}$, check if $\Pi (\pmb {t})$ is not empty and if so, return any schedule $\pi _{\pmb {t}}\in \Pi (\pmb {t})$. We now show that this auxiliary problem can be solved in polynomial time. Given $\pmb {t}$, we first form scenario set $\Gamma '$ by specifying the following parameters for each $S_i \in \Gamma$ and $j\in J$:

• $p_j(S_i')=p_j(S_i)$,

• $\displaystyle d_j(S_i')=\max \{C\ge 0\,:\,w_j(S_i)(C-d_j(S_i))\le t_i\}=t_i/w_j(S_i)+d_j(S_i)$,

• $w_j(S_i')=1$.

The scenario set $\Gamma '$ can be determined in O(Kn) time. We solve Min-Max $1|prec|\max w_j T_j$ with the scenario set $\Gamma '$ by Algorithm 1 obtaining schedule $\pi$. If the maximum cost of $\pi$ over $\Gamma '$ is 0, then $\pi _{\pmb {t}}=\pi$; otherwise $\Pi (\pmb {t})$ is empty. Since Min-Max $1|prec|\max w_j T_j$ is solvable in $O(Kn^2)$ time, the auxiliary problem is solvable in $O(Kn^2)$ time as well. We now show that there exists a vector $\pmb {t}^*=(t_1^*,\dots , t^*_K)$, where $t_i^*\in \{0,\ldots ,f_{\max }\}$, $i\in [K]$, such that each $\pi _{\pmb {t}^*}\in \Pi (\pmb {t}^*)$ minimizes ${\mathrm {OWA(\pi )}}$. Let $\pi ^*$ be an optimal schedule and let $\pmb {t^*}=(t^*_1,\dots ,t^*_K)$ be a vector such that $t^*_i=f(\pi ^*,S_i)$ for $i\in [K]$. Clearly, $t^*_i\in \{0,\dots ,f_{\max }\}$ for each $i\in [K]$ and $\pi ^* \in \Pi (\pmb {t^*})$. By the definition of $\pmb {t^*}$, it holds ${\mathrm {owa}}_{\pmb {v}}(\pmb {t^*})={\mathrm {OWA}}(\pi ^*)$. For any $\pi \in \Pi (\pmb {t^*})$ it holds $f(\pi ,S_i)\le t^*_i= f(\pi ^*,S_i)$, $i\in [K]$. From the monotonicity of OWA, we conclude that each $\pi \in \Pi (\pmb {t^*})$ must be optimal. The algorithm enumerates all possible vectors $\pmb {t}$ and computes $\pi _{\pmb {t}}\in \Pi (\pmb {t})$ if $\Pi (\pmb {t})$ is nonempty. A schedule $\pi _{\pmb {t}}$ with the minimum value of ${\mathrm {owa}}_{\pmb {v}}(\pmb {t})$ is returned. The number of vectors $\pmb {t}$ which must be enumerated is at most $f_{\max }^K$. Hence the problem is solvable in pseudopolynomial time provided that K is constant and the running time of the algorithm is $O(f_{\max }^K Kn^2)$. $\square$

4.3 Approximation algorithm

When K is a part of the input, i.e., in the unbounded case, then the exact algorithm proposed in Sect. 4.2.4 may be inefficient. Notice, that due to Theorem 1, no efficient approximation algorithm can exist for Min-Owa $1|prec|\max w_j T_j$ in this case unless P=NP. We now prove the following result, which can be used to obtain an approximate solution in some special cases of the weight distributions in the OWA operator.

Theorem 7

Suppose that $v_1=\dots =v_{k-1}=0$ and $v_k>0$, $k\in [K]$. Let $\hat{\pi }$ be an optimal solution to the Min-Quant(k) $1|prec|\max w_j T_j$ problem. Then for each $\pi \in \Pi$, it holds $\mathrm{OWA}(\hat{\pi })\le (1/v_k)\mathrm{OWA}(\pi )$ and the bound is tight.

Proof

Let $\sigma$ be a sequence of [K] such that $f(\hat{\pi },S_{\sigma (1)})\ge \cdots \ge f(\hat{\pi },S_{\sigma (K)})$ and $\rho$ be a sequence of [K] such that $f(\pi ,S_{\rho (1)})\ge \cdots \ge f(\pi ,S_{\rho (K)})$. It holds:

$$\begin{aligned} \mathrm{OWA}(\hat{\pi })=\sum _{i=k}^K v_i f(\hat{\pi },S_{\sigma (i)})\le f(\hat{\pi },S_{\sigma (k)}). \end{aligned}$$

From the definition of $\hat{\pi }$ and the assumption that $v_k>0$ we get

$$\begin{aligned} f(\hat{\pi },S_{\sigma (k)})\le & {} f(\pi ,S_{\rho (k)})\le \frac{1}{v_k}\sum _{i \in [K]} v_i f(\pi ,S_{\rho (i)})\\= & {} \frac{1}{v_k}\mathrm{OWA}(\pi ). \end{aligned}$$

Hence $\mathrm{OWA}(\hat{\pi })\le (1/v_k)\mathrm{OWA}(\pi )$. To see that the bound is tight consider an instance of the problem with K scenarios and 2K jobs. The job processing times and weights are equal to 1 under all scenarios. The job due dates are shown in Table 4. We fix $v_i=(1/K)$ for each $i\in [K]$.

Since $v_1>0$, we solve Min-Max $1|prec|\max w_j T_j$. As a result we can obtain the schedule $\pi =(J_2,J_1,J_4,J_3,\ldots ,J_{2K},J_{2K-1})$ whose average cost over all scenarios is 1. But the average cost of the optimal schedule $\pi ^*=(J_1,J_2,J_3,J_4,\dots ,J_{2K-1},J_{2K})$ is 1 / K. $\square$

We now show several consequences of Theorem 7. Observe first that if $v_1>0$, then we can use Algorithm 1 to obtain the approximate schedule in polynomial time.

Corollary 1

If $v_1>0$, then Min-Owa $1|prec|\max w_j T_j$ is approximable within $1/v_1$.

Consider now the case of nondecreasing weights, i.e., $v_1\ge v_2\ge \dots \ge v_K$. Recall that nondecreasing weights are used when the idea of robust optimization is adopted. Namely, larger weights are assigned to larger schedule costs. Since in this case the inequality $v_1\ge 1/K$ must hold, we get the following result:

Corollary 2

If the weights are nonincreasing, then Min-Owa $1|prec|\max w_j T_j$ is approximable within $1/v_1\le K$.

Finally, the following corollary is an immediate consequence of the previous corollary:

Corollary 3

Min-Average $1|prec|\max w_j T_j$ is approximable within K.

Table 4 An example of due date scenario set for which the approximation algorithm achieves a ratio of $1/v_k$

5 The weighted sum of completion times cost function

Let the cost of schedule $\pi$ under scenario $S_i$ be the weighted sum of completion times in $S_i$, i.e., $f(\pi ,S_i)=\sum _{j\in J} w_j(S_i) C_j(\pi ,S_i)$. Using the Graham’s notation, the deterministic version of the problem is denoted by $1|prec|\sum w_j C_j$. We will also examine the special cases of this problem with no precedence constraints between the jobs, i.e., $1||\sum w_j C_j$ and all job weights equal to 1, i.e., $1||\sum C_j$. It is well known that $1|prec|\sum C_j$ is strongly NP-hard for arbitrary precedence constraints (Lenstra and Rinnooy Kan 1978). It is, however, polynomially solvable for some special cases of the precedence constraints such as in-tree, out-tree, or sp-graph (see, e.g., Brucker 2007). If there are no precedence constraints between the jobs, then an optimal schedule can be obtained by ordering the jobs with respect to nondecreasing ratios $p_j/w_j$, which reduces to the SPT rule when all job weights are equal to 1.

In this section, we will show that if the number of scenarios is a part of the input, then Min-Owa $1||\sum w_j C_j$ is strongly NP-hard and not at all approximable. This is the case when the weights in the OWA criterion are nondecreasing, or OWA is the median. We then propose several approximation algorithms which will be valid for nonincreasing weights and the Hurwicz criterion.

5.1 Hardness of the problem

The Min-Max $1||\sum w_j C_j$ and Min-Max $1||\sum C_j$ problems have been recently investigated in literature, and the following results have been established:

Theorem 8

(Yang and Yu 2002) Min-Max $~1||\sum C_j$ is NP-hard even for $K=2$.

Theorem 9

(Mastrolilli et al. 2013) If the number of scenarios is unbounded, then

• (i) Min-max $1||\sum w_j C_j$ is strongly NP-hard and not approximable within $O(\log ^{1-\varepsilon }n)$ for any $\varepsilon >0$ unless the problems in NP have quasi-polynomial time algorithms.

• (ii) Min-max $1||\sum C_j$ and Min-max $1|p_j=1|\sum w_j C_j$ are strongly NP-hard and not approximable within $6/5-\varepsilon$ for any $\varepsilon >0$ unless P=NP.

We now show that the general case is much more complex.

Theorem 10

If the number of scenarios is unbounded, then Min-Owa $1||\sum w_j C_j$ is strongly NP-hard and not at all approximable unless P=NP.

Proof

We show a polynomial time reduction from the Min 2-Sat problem which is known to be strongly NP-hard (see the proof of Theorem 1). Given an instance of Min 2-Sat, we construct the corresponding instance of Min-Owa $1||\sum w_j C_j$ in the following way. We associate two jobs $J_{x_i}$ and $J_{\overline{x}_i}$ with each variable $x_i$, $i\in [n]$. We then set $K=m$ and form scenario set $\Gamma$ in the following way. Scenario $S_k$ corresponds to clause $C_k=(l_1 \vee l_2)$. For $q=1,2$, if $l_q=x_i$, then the processing time of $J_{x_i}$ is 0, the weight of $J_{x_i}$ is 1, the processing time of $J_{\overline{x}_i}$ is 1, and the weight of $J_{\overline{x}_i}$ is 0; if $l_q=\overline{x}_i$, then the processing time of $J_{x_i}$ is 1, the weight of $J_{x_i}$ is 0, the processing time of $J_{\overline{x}_i}$ is 0 and the weight of $J_{\overline{x}_i}$ is 1. If neither $x_i$ nor $\overline{x}_i$ appears in $C_k$, then both processing times and weights of $J_{x_i}$ and $J_{\overline{x}_i}$ are set to 0. We complete the reduction by fixing $v_1=v_2=\dots =v_L=0$ and $v_{L+1}=\dots v_K=1/(m-L)$. A sample reduction is presented in Table 5.

We now show that there is an assignment to the variables which satisfies at most L clauses if and only if there is a schedule $\pi$ such that ${\mathrm {OWA}}(\pi )=0$. Assume that there is an assignment $x_i$, $i\in [n]$, that satisfies at most L clauses. According to this assignment we build a schedule $\pi$ as follows. We first process n jobs $J_{z_i}$, $z_i\in \{x_i, \overline{x}_i\}$, which correspond to false literals $z_i$, $i\in [n]$, in any order and then the rest n jobs that correspond to true literals $z_i$, $i\in [n]$, in any order. Choose a clause $C_k=(l_1 \vee l_2)$ which is not satisfied. It is easy to check that the cost of the schedule $\pi$ under scenario $S_k$ is 0. Consequently, there are at most L scenarios under which the cost of $\pi$ is positive and, according to the definition of the weights in the OWA operator, we get ${\mathrm {OWA}}(\pi )=0$. Suppose now that there is a schedule $\pi$ such that ${\mathrm {OWA}}(\pi )=0$. We construct an assignment to the variables by setting $x_i=0$ if $J_{x_i}$ appears before $J_{\overline{x}_i}$ in $\pi$ and $x_i=1$ otherwise. Since ${\mathrm {OWA}}(\pi )=0$, the cost of $\pi$ must be 0 under at least $m-L$ scenarios. If the cost of $\pi$ is 0 under scenario $S_k$ corresponding to the clause $C_k$, then the assignment does not satisfy $C_k$. Hence, there is at least $m-L$ clauses that are not satisfied and, consequently, at most L satisfiable clauses. $\square$

Corollary 4

Min-Median $1||\sum w_j C_j$ is strongly NP-hard and not at all approximable unless P=NP.

Table 5 Processing times and weights $(p_j(S_i), w_j(S_i))$ corresponding to the formula $(x_1\vee \overline{x}_2)\wedge (\overline{x}_2 \vee \overline{x}_3) \wedge (\overline{x}_1 \vee \overline{x}_4) \wedge (x_1 \vee x_3) \wedge (x_1 \vee \overline{x}_4)$

Proof

The proof is similar to the proof of Theorem 1 and consists in adding some additional scenarios to an instance of problem constructed in Theorem 10. $\square$

5.2 Approximation algorithms

In this section, we show several approximation algorithms for Min-Owa $1|prec|\sum w_j C_j$. We will explore the case in which the weights in the OWA criterion are nonincreasing, i.e., $v_1\ge v_2 \ge \dots \ge v_K$. We will then apply the obtained results to the Hurwicz criterion. Observe, that the case with nondecreasing weights, i.e., $v_1\le v_2\le \dots \le v_K$, is not at all approximable (see the proof of Theorem 10). We first recall a well known property (see, e.g., Mastrolilli et al. 2013) which states that each problem with uncertain processing times and deterministic weights can be transformed into an equivalent problem with uncertain weights and deterministic processing times (and vice versa). This transformation is cost preserving and works as follows. Under each scenario $S_i$, $i\in [K]$, we invert the role of processing times and weights obtaining scenario $S'_i$. The new scenario set $\Gamma '$ contains scenario $S'_i$ for each $i\in [K]$. We also invert the precedence constraints, i.e., if $i\rightarrow j$ in the original problem, then $j\rightarrow i$ in the new one. It can be easily shown that the cost of schedule $\pi$ under S is equal to the cost of the inverted schedule $\pi '=(\pi (n),\ldots ,\pi (1))$ under $S'$. Consequently ${\mathrm {OWA}}(\pi )$ under $\Gamma$ equals ${\mathrm {OWA}}(\pi ')$ under $\Gamma '$. Notice that if the processing times are deterministic in the original problem, then the weights become deterministic in the new one (and vice versa).

Let $w_{\max }, w_{\min }, p_{\max }, p_{\min }$ be the largest (smallest) weight (processing time) in the input instance. We first consider the case then both processing times and weights can be uncertain. We prove the following result:

Theorem 11

If $v_1\ge v_2\ge \dots \ge v_K$ and the deterministic $1|prec|\sum w_j C_j$ problem is polynomially solvable, then Min-Owa $1|prec|\sum w_j C_j$ is approximable within $K\cdot \min \{\frac{w_{\max }}{w_{\min }},\frac{p_{\max }}{p_{\min }}\}$.

Proof

Let $\hat{p}_j=\sum _{i \in [K]} p_j(S_i)$, $\hat{w}_j=\mathrm{owa}_{\pmb {v}}(w_j(S_1),\dots ,w_j(S_K))$, $\hat{C}_j(\pi )=\sum _{i\in [K]} C_j(\pi ,S_i)$, and $\hat{f}(\pi )=\sum _{j\in J} \hat{w}_j\hat{C}_j(\pi )$. Let $\hat{\pi }\in \Pi$ minimize $\hat{f}(\pi )$. Of course, $\hat{\pi }$ can be computed in polynomial time provided that the deterministic counterpart of the problem is polynomially solvable. Let $\sigma$ be a sequence of [K] such that $f(\hat{\pi },S_{\sigma (1)})\ge \dots \ge f(\hat{\pi },S_{\sigma (K)})$. It holds

$$\begin{aligned} \mathrm{OWA}(\hat{\pi })= & {} \displaystyle \sum _{i\in [K]} v_i\sum _{j\in J} w_j(S_{\sigma (i)})C_j(\hat{\pi },S_{\sigma (i)})\nonumber \\\le & {} \sum _{j\in J} \sum _{i\in [K]} v_iw_j(S_{\sigma (i)})\hat{C}_j(\hat{\pi }) \nonumber \\= & {} \sum _{j\in J}\hat{C}_j(\hat{\pi }) \sum _{i\in [K]} v_iw_j(S_{\sigma (i)})\nonumber \\\le & {} \sum _{j \in J} \hat{w}_j \hat{C}_j(\hat{\pi })=\hat{f}(\hat{\pi }), \end{aligned}$$

(5)

where the inequality $\hat{w}_j\ge \sum _{i\in [K]} v_i w_j(S_{\sigma (i)})$ follows from the assumption that $v_1\ge v_2\ge \dots \ge v_K$. We also get for any $\pi \in \Pi$

$$\begin{aligned} \displaystyle \hat{f}(\hat{\pi })\le & {} \displaystyle \hat{f}(\pi )=\sum _{j \in J} \hat{w}_j \hat{C}_j(\pi )\nonumber \\= & {} \sum _{j \in J} \hat{w}_j \sum _{i\in [K]} C_j(\pi ,S_i)\nonumber \\\le & {} \frac{w_{\max }}{w_{\min }}\sum _{j\in J}\sum _{i\in [K]}w_j(S_i)C_j(\pi ,S_i)\nonumber \\= & {} \displaystyle =\frac{w_{\max }}{w_{\min }}\sum _{i\in [K]}\sum _{j\in J}w_j(S_i)C_j(\pi ,S_i), \end{aligned}$$

(6)

where the second inequality follows from the fact that $\hat{w_j}\le w_{\max }\le (w_{\max }/w_{\min })w_j(S_i)$ for each $j\in J$, $i\in [K]$. Again, from the assumption that $v_1\ge v_2\ge \dots \ge v_K$ we have

$$\begin{aligned} (1/K)\sum _{i\in [K]}\sum _{j\in J}w_j(S_i)C_j(\pi ,S_i)\le \mathrm{OWA}(\pi ). \end{aligned}$$

(7)

From (5), (6), and (7) we get $\mathrm{OWA}(\hat{\pi })\le K\cdot \frac{w_{\max }}{w_{\min }}\mathrm{OWA}(\pi ).$ Since the role of job processing times and weights can be inverted we also get $\mathrm{OWA}(\hat{\pi })\le K\cdot \frac{p_{\max }}{p_{\min }}\mathrm{OWA}(\pi )$ and the theorem follows. $\square$

In Mastrolilli et al. (2013) a 2-approximation algorithm for Min-Max $1|prec|\sum w_j C_j$ has been recently proposed, provided that either job processing times or job weights are deterministic (they do not vary among scenarios). In this section, we will show that this algorithm can be extended to Min-Owa $1|prec|\sum w_jC_j$ under the additional assumption that the weights in the OWA operator are nonincreasing, i.e., $v_1\ge v_2\ge \dots \ge v_K$. The idea of the approximation algorithm is to design a mixed integer programming formulation for the problem, solve its linear relaxation, and construct an approximate schedule based on the optimal solution to this relaxation.

Assume now that job processing times are deterministic and equal to $p_j$ under each scenario $S_i$, $i\in [K]$. Let $\delta _{ij}\in \{0,1\}$, $i,j\in [n]$, be binary variables such that $\delta _{ij}=1$ if job i is processed before job j in a schedule constructed. The vectors of all feasible job completion times $(C_1,\ldots , C_n)$ can be described by the following system of constraints (Potts 1980):

$$\begin{aligned} \begin{array}{llll} VC: &{} C_j=p_j+\sum _{i\in J{\setminus }\{j\}} \delta _{ij} p_i &{}\,\, j\in J\\ &{}\delta _{ij}+\delta _{ji}=1 &{}\,\, i,j\in J, i\ne j \\ &{}\delta _{ij}+\delta _{jk}+\delta _{ki} \ge 1 &{}\,\, i,j,k \in J\\ &{}\delta _{ij}=1 &{}\,\, i\rightarrow j\\ &{}\delta _{ij}\in \{0,1\}&{}\,\, i,j \in J \end{array} \end{aligned}$$

(8)

Let us denote by $VC'$ the relaxation of VC, in which the constraints $\delta _{ij}\in \{0,1\}$ are replaced with $0\le \delta _{ij}\le 1$. It has been proved in Schulz (1996a, b) (see also Hall et al. 1997) that each vector $(C_1,\ldots , C_n)$ that satisfies $VC'$ also satisfies the following inequalities:

$$\begin{aligned} \sum _{j\in I} p_jC_j\ge \frac{1}{2}\left( \left( \sum _{j\in I} p_j\right) ^2+\sum _{j\in I} p_j^2\right) \text { for all } I \subseteq J \end{aligned}$$

(9)

In order to build a MIP formulation for the problem, we will use the idea of a deviation model introduced in Ogryczak and Śliwiński (2003). Let $\sigma$ be a permutation of [K] such that $f(\pi ,S_{\sigma (1)})\ge \dots \ge f(\pi ,S_{\sigma (K)})$ and let $\theta _k(\pi )=\sum _{i=1}^k f(\pi ,S_{\sigma (i)})$ be the cumulative cost of schedule $\pi$. Define $v'_i=v_i-v_{i+1}$ for $i=1,\dots ,K-1$ and $v'_K=v_K$. An easy verification shows that

$$\begin{aligned} \mathrm{OWA}(\pi )=\sum _{k=1}^K v'_k \theta _k(\pi ). \end{aligned}$$

(10)

Lemma 1

Given $\pi$, the value of $\theta _k(\pi )$ can be obtained by solving the following linear programming problem:

$$\begin{aligned} \begin{array}{lllll} \min &{} \sum _{i=1}^K u_{i} - (K-k) r \\ &{} r\le u_{i} &{} i\in [K] \\ &{} u_{i} \ge f(\pi ,S_i) &{} i\in [K] \\ &{} u_i \ge 0 &{} i\in [K]\\ &{} r\ge 0 \end{array} \end{aligned}$$

(11)

Proof

Consider the following linear programming problem:

$$\begin{aligned} \begin{array}{lllll} \max &{} \sum _{i=1}^K \beta _i f(\pi ,S_i) \\ &{} \alpha _i + \beta _i \le 1 &{} i\in [K] \\ &{} \sum _{i=1}^K \alpha _i \ge (K-k)\\ &{} \alpha _i, \beta _i \ge 0 &{} i\in [K] \end{array} \end{aligned}$$

(12)

It is easy to see that an optimal solution to (12) can be obtained by setting $\beta _{\sigma (i)}=1$ and $\alpha _{\sigma (i)}=0$ for $i=1\dots k$, $\beta _{\sigma (i)}=0$ and $\alpha _{\sigma (i)}=1$ for $i=k+1,\dots K$, where $\sigma$ is such that $f(\pi ,S_{\sigma (1)})\ge \dots \ge f(\pi ,S_{\sigma (K)})$. This gives us the maximum objective function value equal to $\theta _k(\pi )$. To complete the proof it is enough to observe that (11) is the dual linear program to (12). $\square$

If $v_1\ge v_2\ge \dots \ge v_K$, then $v'_i\ge 0$ and (8), (10), (11) lead to the following mixed integer programming formulation for the problem:

$$\begin{aligned} \begin{array}{lllll} \min &{} \sum _{k=1}^K v'_k (\sum _{i=1}^K u_{ik} - (K-k) r_k) \\ &{} \text {Constraints } VC \\ &{} r_k\le u_{ik} &{} i,k\in [K] \\ &{} u_{ik} \ge \sum _{j\in J} C_j w_j(S_i) &{} i,k\in [K] \\ &{} u_{ik} \ge 0 &{} i,k\in [K]\\ &{} r_k\ge 0 &{} k\in [K] \\ \end{array} \end{aligned}$$

(13)

In order to construct the approximation algorithm we will also need the following easy observation:

Observation 1

Let $(f_1,\dots , f_K)$ and $(g_1,\dots ,g_K)$ be two nonnegative real vectors such that $f_i\le \gamma g_i$ for some constant $\gamma >0$. Then, ${\mathrm {owa}}_{\pmb {v}}(f_1,\dots , f_k)\le \gamma {\mathrm {owa}}_{\pmb {v}}(g_1,\dots , g_K)$ for each $\pmb {v}$.

Proof

From the monotonicity of the OWA operator and the assumption $\gamma >0$, it follows that $\mathrm{owa}_{\pmb {v}}(f_1,\dots ,f_K)\le \mathrm{owa}_{\pmb {v}}(\gamma g_1,\dots ,\gamma g_K)=\gamma \mathrm{owa}_{\pmb {v}}(g_1,\dots ,g_K)$. $\square$

The approximation algorithm works as follows. We first solve the linear relaxation of (13) in which VC is replaced with $VC'$ . Clearly, this relaxation can be solved in polynomial time. Let $(C_1^*, \dots , C_n^*)$ be the relaxed optimal job completion times and $z^*$ be the optimal value of the relaxation. It holds $z^*={\mathrm{owa}}_{\pmb {v}}(\sum _{j\in J} C^*_j w_j(S_1), \dots , \sum _{j\in J} C^*_j w_j(S_K))$. We now relabel the jobs so that $C^*_1\le C^*_2\le \dots \ C_n^*$ and form schedule $\pi =(1,2,\dots ,n)$. Since the vector $(C_j^*)$ satisfies $VC'$ it must also satisfy (9). Hence, by setting $I=\{1,\dots ,j\}$, we get

$$\begin{aligned} \sum _{i=1}^j p_iC^*_i\ge \frac{1}{2}\left( \left( \sum _{i=1}^j p_i \right) ^2+\sum _{i=1}^j p_i^2\right) \ge \frac{1}{2} \left( \sum _{i=1}^j p_i \right) ^2. \end{aligned}$$

Since $C^*_j\ge C_i^*$ for each $i\in \{1\dots j\}$, we get $C^*_j\sum _{i=1}^j p_i\ge \sum _{i=1}^j p_iC^*_i \ge \frac{1}{2}(\sum _{i=1}^j p_i)^2$ and, finally $C_j=\sum _{i=1}^j p_i \le 2 C^*_j$ for each $j\in J$ – this reasoning is the same as in Schulz (1996b). For each scenario $S_i$, $i\in [K]$, it holds $f(\pi ,S_i)=\sum _{j\in J} C_j w_j(S_i)\le 2 \sum _{j\in J} C^*_j w_j(S_i)$, and Observation 1 implies

$$\begin{aligned} \mathrm{OWA}(\pi )= & {} \mathrm{owa}_{\pmb {v}}\left( \sum _{j\in J} C_j w_j(S_1), \dots , \sum _{j\in J} C_j w_j(S_K)\right) \\\le & {} 2z^*. \end{aligned}$$

Since $z^*$ is a lower bound on the value of an optimal solution, $\pi$ is a 2-approximate schedule. Let us summarize the obtained result.

Theorem 12

If $v_1\ge v_2\ge \dots \ge v_K$, and job processing times (or weights) are deterministic, then Min-Owa $1|prec|\sum w_j C_j$ is approximable within 2.

We now use Theorem 12 to prove the following result:

Theorem 13

Min-Hurwicz $1|prec|\sum w_j C_j$ is approximable within 2, if job processing times (or weights) are deterministic.

Proof

Assume that job processing times are deterministic (the reasoning for deterministic processing times is the same). The problem with the Hurwicz criterion can be rewritten as follows:

$$\begin{aligned} \min _{\pi \in \Pi } \mathrm{OWA}(\pi )= \min _{\pi \in \Pi }\min _{k\in [K]} H_k(\pi ), \end{aligned}$$

where

$$\begin{aligned}&H_k(\pi )\\&\,\,=\alpha \max _{i \in [K]} \sum _{j\in J} w_j(S_i)C_j(\pi ) + (1-\alpha ) \sum _{j\in J} w_j(S_k)C_j(\pi )\\&\,\,=\max _{i \in [K]}\left( \alpha \sum _{j\in J} w_j(S_i)C_j(\pi ) + (1-\alpha ) \sum _{j\in J} w_j(S_k)C_j(\pi )\right) \\&\,\,=\max _{i\in [K]} \sum _{j\in J} \hat{w}_j(S_i)C_j(\pi ), \end{aligned}$$

where $\hat{w}_j(S_i)=\alpha w_j(S_i)+(1-\alpha )w_j(S_k)$. Hence the problem reduces to solving K auxiliary Min-Max $1|prec|\sum w_j C_j$ problems. Since Min-Max $1|prec|\sum w_j C_j$ is approximable within 2 (see Mastrolilli et al. 2013, or Theorem 12), the theorem follows. $\square$

6 Conclusion and open problems

In this paper, we have proposed a new approach to scheduling problems with uncertain parameters. The key idea is to use the OWA operator to aggregate all possible values of the schedule cost. The weights in OWA allow decision makers to take their attitude towards a risk into account. In consequence, the main advantage of the proposed approach is to weaken the very conservative min-max criterion, traditionally used in robust optimization. Apart from proposing a general framework, we have discussed the computational properties of two basic single machine scheduling problems. We have shown that they have various computational and approximation properties, which make their analysis very challenging. However, there is still a number of open problems regarding the considered cases. For the problem with the maximum weighted tardiness criterion, we do not know if the problem is weakly NP-hard when the number of scenarios is constant (the bounded case). It may be also the case that the pseudopolynomial algorithm designed for a fixed K can be converted into a polynomial one by using a similar idea as for the Hurwicz criterion. We also do not know if the problem with the average criterion admits an approximation algorithm with a constant worst-case ratio (we only know that it is approximable within K and not approximable within a ratio less than 7/6). For the problem with the weighted sum of completion times criterion, the complexity of ${\textsc {Min-Average}}~1||\sum w_jC_j$ with uncertain processing times and weights is open. The framework proposed in this paper can also be applied to other scheduling problems, for example to the single machine scheduling problem with the sum of late jobs criterion (the min-max version of this problem was discussed in Aissi et al. 2011; Aloulou and Croce 2008).