Abstract
Assessment of the elimination of an oral test dose based on plasma concentration values requires correction for the effect of gastric release and absorption. Irregular uptake processes should be described ‘model independently’, which requires estimation of a large number of absorption parameters. To limit the associated computational effort a new approach is developed with a reduced number of unknown parameters. A marginalized and regularized absorption approach (MRA) is defined, which uses for the uptake just one parameter to control rigidity of the uptake curve. For validation, elimination and absorption were reproduced using published IVIVC data and a synthetic data set for comparison with approaches using a ‘model-free’—staircase function or mechanistic models to describe absorption. MRA performed almost as accurate as well specified mechanistic models, which gave the best reproduction. MRA demonstrated a 50fold increase in computational efficiency compared to other approaches. The absorption estimated for the IVIVC study demonstrated an in vivo–in vitro correlation comparable to published values. The newly developed MRA approach can be used to efficiently and accurately estimate elimination and absorption with a restricted number of adaptive parameters and with automatic adjustment of the complexity of the uptake.



Similar content being viewed by others
References
Csajka C, Drover D, Verotta D (2005) The use of a sum of inverse Gaussian functions to describe the absorption profile of drugs exhibiting complex absorption. Pharm Res. 22: 1227–1235
Zhou H (2003) Pharmacokinetic strategies in deciphering atypical drug absorption profiles. J Clin Pharmacol. 43(3):211–227
Lipka E, Lee ID, Langguth P, Spahn-Langguth H, Mutschler E, Amidon G (1995) Celiprolol double-peak occurrence and gastric motility: nonlinear mixed effects modeling of bioavailability data obtained in dogs. J Pharmacokinet Biopharm. 23:267–286
Gerlowski LE, Jain RK (1983) Physiologically based pharmacokinetic modeling: principles and applications. J Pharm Sci. 72(10):1103–1127
Blakey G, Nestorov I, Arundel P, Aarons L, Rowland M (1997) Quantitative structure-pharmacokinetics relationships: I. Development of a whole-body physiologically based model to characterize changes in pharmacokinetics across a homologous series of barbiturates in the rat. J Pharmacokinet Biopharm. 25:277–312
Yu LX, Amidon GL (1999) A compartmental absorption and transit model for estimating oral drug absorption. Int J pharm. 186(2):119–125
Di Muria M, Lamberti G, Titomanlio G (2010) Physiologically based pharmacokinetics: a simple, all purpose model. Ind Eng Chem Res. 49(6):2969–2978
Savic RM, Jonker DM, Kerbusch T, Karlsson MO (2007) Implementation of a transit compartment model for describing drug absorption in pharmacokinetic studies. J Pharmacokinet Pharmacodyn. 34(5):711–726
Weiss M (1984) A note on the rôle of generalized inverse Gaussian distributions of circulatory transit times in pharmacokinetics. J Math Biol. 20:95–102
Wikipedia (2011) Inverse Gaussian distribution—Wikipedia, The free encyclopedia http://en.wikipedia.org/wiki/InverseGaussiandistribution.
Higaki K, Yamashita S, Amidon GL (2001) Time-dependent oral absorption models. J Pharmacokinet Pharmacodyn. 28(2):109–128
Karlsson M, Beal S, Sheiner L (1995) Three new residual error models for population PK/PD analyses. J Pharmacokinet Pharmacodyn. 23(6):651–672
Iga K, Ogawa Y, Yashiki T, Shimamoto T (1986) Estimation of drug absorption rates using a deconvolution method with nonequal sampling times. J Pharmacokinet Pharmacodyn. 14(2):213–225
Lindberg-Freijs A, Karlsson MO (1994) Dose dependent absorption and linear disposition of cyclosporin A in rat. Biopharm Drug Disposit. 15(1):75–86
Fattinger K, Verotta D (1995) A nonparametric subject-specific population method for deconvolution: I. Description, internal validation, and real data examples. J Pharmacokinet Pharmacodyn. 23:581–610
Wikipedia (2011) Splines (mathematics)—Wikipedia, The free encyclopedia http://en.wikipedia.org/wiki/Spline_mathematics.
Mason JC, Handscomb DC (2003) Chebyshev polynomials. Chapman and Hall/CRC press, Boca Raton
Park K, Verotta D, Blaschke TF, Sheiner LB (1997) A semiparametric method for describing noisy population pharmacokinetic data. J Pharmacokinet Pharmacodyn. 25(5):615–642
Hastie T, Tibshirani R, Friedman JH (2008) The elements of statistical learning 2nd edn. Springer, New york
Bishop CM (2007) Pattern recognition and machine learning (information science and statistics), 1st edn. Springer, New york
Dormand JR, Prince PJ (1980) A family of embedded Runge-Kutta formulae. J Comput Appl Math. 6(1):19–26
Powell MJD (2009) The BOBYQA algorithm for bound constrained optimization without derivatives. Centre for mathematical sciences, University of Cambridge, UK. Report DAMTP 2009/NA06. http://www.damtp.cam.ac.uk/user/na/NA_papers/NA2009_06.pdf
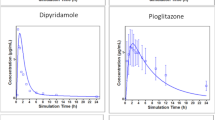
Dutta S, Qiu Y, Samara E, Cao G, Granneman GR (2005) Once-a-day extended-release dosage form of divalproex sodium III: Development and validation of a level A in vitro–in vivo correlation (IVIVC). J Pharm Sci. 94(9):1949–1956
DiMuria M, Lamberti G, Titomanlio G (2009) Modeling the pharmacokinetics of extended release pharmaceutical systems. Heat Mass Transfer. 45(5):579–589
Press W, Teukolsky S, Vetterling W, Flannery B (2002) Numerical recipes in C++: the art of scientific computing. Cambridge University Press, Cambridge
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Appendix 1: Operations on polynomials
Let P(t) be a polynomial of n-th order, which approximates the function p(t), let p g be a vector of values of p(t) at grid points g = \({t_0,\cdots,t_n}\). Important operations are the calculation of grid values from coefficients, and its reverse:
derivatives of polynomials
Let P(t) K the vector of values of the polynomial(K = 0) to k-th derivative of the polynomial (K = k) at point t:
The concatenation of the operations 16c with 16b yields \({\dot{\bf x}}={\bf D}_{g} {\bf B}_{g} {\bf x}\), the time derivatives of x at grid points as a function of x. The product matrix D g B g is square and singular, hence the row for \(\dot{x}\) at t = 0 is cancelled and the state variable x is scaled such that x(t = 0) = 0, which allows to cancel also the column of D g B g pertaining to x(t = 0). The resulting matrix D 1 is non singular. Mason shows [17, chap.10.5], that a grid located at the maxima of a n-dimensional chebyshev polynomial leads to an optimal approximation. The accuracy and numerical efficacy of the ‘collocation’ approach can be demonstrated for a one compartment system an uptake given in Eq. 14. With this uptake an exact solution can be defined for Eq. 1. It is, with d 1 = k el − tr 1, d 2 = k el − tr 2, k 1 = f 1 tr 41 /d 41 , k 2 = (1 − f 1) tr 42 /d 42 :
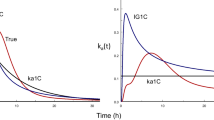
This solution and parameters from test case A, Fig. 1 is used as a reference and to compare it with results obtained with iterative numerical integration [21, ode45, MATLAB]. Table 6 demonstrates that the numerical effort for the ’collocation’-approach to achieve a given accuracy is comparable to that of a conventional numerical integration.
The optimal grid with points at the maxima of a n-dimensional chebyshev polynomial does not match the time grid defined by the measurement points. For adaptation the experimental time t, ranging from 0 to 3 h is transformed to an ‘internal time’ s with the range −1, +1. A nonlinear grid-transformation is used to spread a time interval at the first phase of the experiment. This widens needle shaped uptake peaks, which are otherwise difficult to approximate based on polynomials. The transformations involved are denoted as \(s=f(t_s)=2.12 \sqrt{t_s/3} -1.12,\,t_s=\hbox{max}(t,0.018);\,t=g(s)=\frac{3}{4}(1.06+0.94)^2\) and \(\partial t/\partial s=g_s(s)=\frac{3}{2}(1.06+0.94 s)\). The uptake polynomial then pertains to the transformed time s. For back transformation we consider the vector of polynomial values p, calculated for the internal grid s as p = A s w s . If the s-grid is transformed to the measurement time grid m, then the p values remain the same, they just pertain to a different grid. Hence, one can set for the measurement grid: w m = B m p, which gives, considering how p was calculated, w m = B m A s w s . It converts coefficients for the internal representation to coefficients pertaining to the regular time scale. This conversion is used when the uptake is required in ‘real time’, e.g. at the calculation of the restraints with Eq. 20, where the time derivatives following Eq. 16d were calculated.
Equation 1, when replacing t with g(s) and after multiplication both sides with g s equals:
Replacing k el g s (s) with k * el (s) allows defining a new D 2 which can be used in Eq. 3, similarly \(\varvec{\Uppsi}\) can be extended to absorb the factor g s (s) for each row. The resulting matrix equation pertains to a grid at transformed measurement time points, which does not match the optimal grid for collocation system. For adaptation let x m be the vector of polynomial values at the measurement grid m and x c the values at a grid c, defined by the extremals of a chebychev polynomial, including the value at t = 0. The product of the operations 16b and 16a gives a transformation: x m = A m B c x c . With \({\bf x}_c=\varvec{\Uppsi} {\bf w}\) the Eq. 3 can adapted to the measurement grid as: \({\bf x}_{m}={\bf A}_m {\bf B}_c \varvec{\Uppsi} {\bf w}\) and \(\varvec{\Upphi}\) in Eq. 5 changes to:
Appendix 2: Boundary conditions for the uptake
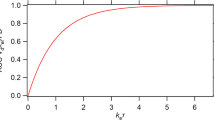
After oral administration the test substance reaches the systemic circulation with a delay. Hence, for the left boundary at t = 0 we can assume zero values for u(t) = 0 and derivatives of all orders from u′(t)≃ 0 bis u IV(t)≃ 0. For the right boundary, the end of the study protocol, we assume that the uptake behaves like an inverse gaussian distribution IG(μ, λ, t) at the time t = 3 and arbitrary λ and μ values. For λ < 1 and μ < 1 the release is completed and the uptake and its derivatives are close to zero. For larger values of μ and λ we find u(t = 3) > 0, u′(t = 3) < 0 and higher order derivatives have the tendency to change signs. To capture this behaviour we defined vectors igf containing derivatives from the zero-th up to the fourth order derivatives of IG(μ, λ, t = 3). 32 vectors for different permutations of 0.5 < μ < 2 and 0.7 < λ < 3 were calculated. The eigenvalues and eigenvectors (denoted as V) of the covariance of these uptake features was determined. The matrix V provides the variance components of the uptake and its derivatives. Hence, the product z = V × igf transforms an igf vector into excursions in the direction of the variance components. These excursions have a mean value \({\overline{\bf z}}\) that is calculated from the mean of \({\overline{\bf igf}}\) and have a variance that equals the eigenvalues of the covariance of igf. With Eq. 16d one obtains P(t) K as polynomial counterpart to a vector igf and the product \({\bf V} \times {\bf P(t)}^{\bf K}= {\bf V} \; {\bf M}_{{\bf t=3}} {\bf w}\) gives the excursions of a polynomial in directions of the variance components. These excursions should have mean values comparable to \(\overline{\bf z}\) and variances matching the eigenvalues of the covariance of the reference igf values, if the polynomials behaves like an inverse gaussian. This allows defining restraints as ancillary measurements (\({\bf r}=\varvec{\Uppsi}_{\bf r} {\bf w}\) in Eq. 4) for the boundaries of the uptake polynomial as:
where M t=0 is defined in Eq. 16d. The upper part for the left boundary has the variance 5 except for u(t = 0), where it is 0.01 and the variances for the lower part are the eigenvalues of the variance of igf.
Appendix 3: Marginal likelihood
The exponents of the product in Eq. 8 were expanded to give:
The terms, squared in w are: \({\bf w}^T \varvec{\Upphi}^{\user2{T}} \varvec{\Upphi} {\bf w} +\alpha {\bf w}^{\bf T} {\bf w}={\bf w}^T(\alpha I+\varvec{\Upphi}^{\user2{T}}\varvec{\Upphi}){\bf w}={\bf w}^{\bf T} {\bf A w}\) with \({\bf A} = \alpha {\bf I}+\varvec{\Upphi}^{\bf T}\varvec{\Upphi}\). The terms, linear in w are: \({\bf t}^{\user2{T}} \varvec{\Upphi} {\bf w}={\user2{T}}^{\bf T}\varvec{\Upphi} {\bf A}^{-1} {\bf A w}=\varvec{\mu}^T{\bf A w}\) and, in analogy: \({\bf w}^{\user2{T}} \varvec{\Upphi}^{\user2{T}} {\bf t}={\bf w}^{\user2{T}} {\bf A} \varvec{\mu}\). ‘Completing’ the squared and linear terms in w with \(\varvec{\mu}^T {\bf A} \varvec{\mu}\) gives a squared term as:
As a compensation, the completing term has to be subtracted from the second distribution, which gives:
and the product of likelihoods can be expressed as
Rights and permissions
About this article
Cite this article
Vogt, J.A., Denzer, C. Estimation of parameters for the elimination of an orally administered test substance with unknown absorption. J Pharmacokinet Pharmacodyn 40, 177–187 (2013). https://doi.org/10.1007/s10928-013-9299-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10928-013-9299-z