Skip to main content
SpringerLink
Log in

Method of Moving Frames to Solve Conservation Laws on Curved Surfaces

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

An Erratum to this article was published on 11 May 2012

Abstract

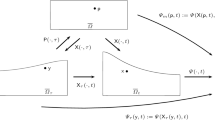
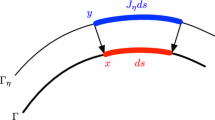
A new numerical framework is proposed to solve partial differential equations on curved surfaces by using the orthogonal moving frames at each grid point to compute the gradient of a scalar variable. We call this framework the method of moving frames (MMF) that is adopted and modified from the works of É. Cartan. Compared to the Eulerian method and the Lagrangian multiplier method, the MMF method uses only the surface as the domain, not additionally the ambient space enclosing it. Also different from directly solving the equations with respect to the curved axis, the MMF method is free of the metric tensors. This uniqueness is the consequence of the virtual and penalty extension of the variables in a special direction, called the exponential direction, instead of the surface normal direction that is typically taken. The exponential extension eliminates the need to extend the computational domain and the variables outside the curved surfaces, but the variables outside the curved surfaces are not extended in the direction of the surface normal, yielding an extension error. However, the overall error for the MMF scheme, caused by the extension error, is of high order in L 2 error with respect to space discretization. This high convergence rate implies that the exponential error can be made negligible compared to the error of differentiation and integration, which are also expressed with space discretization but with lower order, in adaptively-refined meshes proportional to the Gaussian curvature. As the first application of the MMF method, conservation laws are considered on curved surfaces. To display the exponential convergence and the unique features of the MMF scheme, convergence tests are demonstrated on four different types of surfaces: an open spherical shell, a closed spherical shell, an irregular closed surface, and a non-convex closed surface.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Adalsteinsson, D., Sethian, J.A.: Transport and diffusion of material quantities on propagating interfaces via level set methods. J. Comput. Phys. 185(1), 271–288 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  2. Bernard, P.-E., Remacle, J.-F., Comblen, R., Legat, V., Hillewaert, K.: High-order discontinuous Galerkin schemes on general 2D manifolds applied to shallow water equations. J. Comput. Phys. 228(17), 6514–6535 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  3. Bernardi, C., Mayday, Y.: Polynomial interpolation results in Sobolev spaces. J. Comput. Appl. Math. 43, 53–80 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  4. Bertalmio, M., Cheng, L., Osher, S., Sapiro, G.: Variational problems and partial differential equations on implicit surfaces. J. Comput. Phys. 174(2), 759–780 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  5. Christensen, M., Pedersen, J.B.: Diffusion in inhomogeneous and anisotropic media. J. Chem. Phys. 119, 5171–5175 (2003)

    Article  Google Scholar 

  6. Coté, J.: A Lagrange multiplier approach for the metric terms of semi-Lagrangian models on the sphere. Q. J. R. Meteorol. Soc. 114(483), 1347–1352 (1988)

    Google Scholar 

  7. Darboux, G.: Rend. Accad. Lincei 5th Ser. 276–332 (1895)

  8. Davis, P.J.: Interpolation and Approximation. Dover, New York (1975)

    MATH  Google Scholar 

  9. Debbasch, F., Chevalier, C.: Diffusion processes on manifolds. In: Markov Processes and Related Topics: A Festschrift for Thomas G. Kurtz. IMS Collections, vol. 4, pp. 85–97 (2008)

    Chapter  Google Scholar 

  10. Deckelnick, K., Dziuk, G., Elliott, C.M., Heine, C.-J.: An h-narrow band finite-element method for elliptic equations on implicit surfaces. IMA J. Numer. Anal. 30, 351–376 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  11. Cartan, É.: Riemannian Geometry in an Orthogonal Frame. World Scientific, Singapore (2001)

    Book  Google Scholar 

  12. Cartan, É.: Geometry of Riemannian Spaces. Math. Sci. Press, Brookline (2001), translated by R. Hermann

    Google Scholar 

  13. Giraldo, F.X., Hesthaven, J.S., Warburton, T.: Nodal high-order discontinuous Galerkin methods for the spherical shallow water equations. J. Comput. Phys. 181(2), 499–525 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  14. Giraldo, F.X., Perot, J.B., Fischer, P.F.: A spectral element semi-Lagrangian (SESL) method for the spectral shallow water equations. J. Comput. Phys. 20(2), 623–650 (2003)

    Article  MathSciNet  Google Scholar 

  15. Giraldo, F.X.: Lagrange-Galerkin methods on spherical geodesic grids. J. Comput. Phys. 181(1), 197–213 (1997)

    Article  MathSciNet  Google Scholar 

  16. Greer, J.B.: An improvement of a recent Eulerian method for solving PDEs on general geometries. J. Sci. Comput. 29(3), 321–352 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  17. Greer, J.B., Bertozzi, A.L., Sapiro, G.: Fourth order partial differential equations on general geometries. UCLA CAM Report, 05(17), 2005

  18. Hesthaven, J.S., Warburton, T.: Nodal Discontinuous Galerkin Methods: Algorithms, Analysis, and Applications. Springer, Berlin (2007)

    Google Scholar 

  19. Karniadakis, G.E., Sherwin, S.J.: Spectral/hp element Methods for Computational Fluid Dynamics, 2nd edn. Oxford University Press, Oxford (2005)

    Book  MATH  Google Scholar 

  20. Meyer, M., Desbrun, M., Schröder, P., Barr, A.H.: Discrete differential-geometry operators for triangulated 2-manifolds. In: VisMath ’02 Proceedings (2002)

    Google Scholar 

  21. Novak, I.L., Gao, F., Choi, Y.S., Resasco, D., Schaff, J.C., Slepchenko, B.M.: Diffusion on a curved surface coupled to diffusion in the volume: application to cell biology. J. Comput. Phys. 226(2), 1271–1290 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  22. O’Neill, B.: Elementary Differential Geometry, 2nd edn. Academic Press, San Diego (1997)

    MATH  Google Scholar 

  23. Pudykiewicz, J.A.: Numerical solution of the reaction-advection-diffusion equation on the sphere. J. Comput. Phys. 213(1), 358–390 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  24. Ricci, G.: Rend. Accad. Lincei 5th Ser., 19(I), 181–187 (1910)

    MATH  Google Scholar 

  25. Ricci, G.: Rend. Accad. Lincei 5th Ser., 19(II), 85–90 (1910)

    Google Scholar 

  26. Rosenberg, S.: The Laplacian on a Riemannian Manifold. Cambridge University Press, Cambridge (1997)

    Book  MATH  Google Scholar 

  27. Rossmanith, J.A., Bale, D.S., LeVeque, R.J.: A wave propagation algorithm for hyperbolic systems on curved manifolds. J. Comput. Phys. 199, 631–662 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  28. Sapiro, G.: Geometric Partial Differential Equations and Image Analysis. Cambridge University Press, Cambridge (2001)

    Book  MATH  Google Scholar 

  29. Sbalzarini, I.F., Hayer, A., Helenius, A., Koumoutsakos, P.: Simulations of (an)isotropic diffusion on curved biological surfaces. Biophys. J. 90(3), 878–885 (2006)

    Article  Google Scholar 

  30. Schwartz, P., Adalsteinsson, D., Colella, P., Arkin, A.P., Onsum, M.: Numerical computation of diffusion on a surface. Proc. Natl. Acad. Sci. USA 102(32), 11151–11156 (2005)

    Article  Google Scholar 

  31. Sherwin, S.J., Kirby, R.M., et al.: Nektar++: open source software library for the spectral/hp element method. Website: http://www.nektar.info

  32. Spivak, M.: A Comprehensive Introduction to Differential Geometry, vol I, 3rd edn. Publish or Perish, INC, Boston (2005)

    Google Scholar 

  33. Szegő, G.: Orthogonal Polynomials. Colloquium Publications. American Mathematical Society, Providence (1939)

    Google Scholar 

  34. Turing, A.M.: The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. B, Biol. Sci. 237, 37–72 (1953)

    Google Scholar 

  35. Weatherburn, C.E.: An Introduction to Riemannian Geometry and the Tensor Calculus. Cambridge University Press, Cambridge (1957)

    Google Scholar 

  36. Williamson, D.L., Drake, J.B., Hack, J.J., Jakob, R., Shwartzrauber, P.N.: A standard test set for numerical approximations to the shallow water equations in spherical geometry. J. Comput. Phys. 102(1), 211–224 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  37. Xu, G.: Convergence of discrete Laplace-Beltrami operators over surfaces. Comput. Math. Appl. 48, 347–360 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  38. Xu, J., Zhao, H.-K.: An Eulerian formulation for solving partial differential equations along a moving interface. J. Sci. Comput. 19(1–3), 573–594 (2003)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute for Mathematical Sciences, Imperial College London, London, UK, SW7 2PE

    Sehun Chun

  2. African Institute for Mathematical Sciences, 6 Melrose Road, Muizenberg, 7945, South Africa

    Sehun Chun

Authors
  1. Sehun Chun
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sehun Chun.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Chun, S. Method of Moving Frames to Solve Conservation Laws on Curved Surfaces. J Sci Comput 53, 268–294 (2012). https://doi.org/10.1007/s10915-011-9570-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-011-9570-7

Keywords

Search

Navigation