Skip to main content
SpringerLink
Log in

Optimized High-Order Derivative and Dissipation Operators Satisfying Summation by Parts, and Applications in Three-dimensional Multi-block Evolutions

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

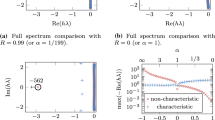
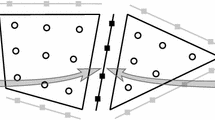
We construct optimized high-order finite differencing operators which satisfy summation by parts. Since these operators are not uniquely defined, we consider several optimization criteria: minimizing the bandwidth, the truncation error on the boundary points, the spectral radius, or a combination of these. We examine in detail a set of operators that are up to tenth order accurate in the interior, and we surprisingly find that a combination of these optimizations can improve the operators’ spectral radius and accuracy by orders of magnitude in certain cases. We also construct high-order dissipation operators that are compatible with these new finite difference operators and which are semi-definite with respect to the appropriate summation by parts scalar product. We test the stability and accuracy of these new difference and dissipation operators by evolving a three-dimensional scalar wave equation on a spherical domain consisting of seven blocks, each discretized with a structured grid, and connected through penalty boundary conditions. In particular, we find that the constructed dissipation operators are effective in suppressing instabilities that are sometimes otherwise present in the restricted full norm case.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Kreiss H.O., Scherer G., (1974). Finite element and finite difference methods for hyperbolic partial differential equations. In: Boor C.D. (eds). Mathematical Aspects of Finite Elements in Partial Differential Equations. Academica Press, New York

    Google Scholar 

  2. Kreiss, H. O., and Scherer, G. (1977). Tech. Rep., Dept. of Scientific Computing, Uppsala University Sweden.

  3. Olsson P. (1995). Summation by Parts, Projections, and Stability I. Math. Comp. 64: 1035

    Article  MATH  MathSciNet  Google Scholar 

  4. Olsson P. (1995). Supplement to “Summation by parts, projections, and stability, I”. Math. Comp. 64: S23

    Article  Google Scholar 

  5. Olsson P. (1995). Summation by Parts, Projections, and Stability II. Math. Comp. 64: 1473

    Article  MATH  MathSciNet  Google Scholar 

  6. Carpenter M., Gottlieb D., Abarbanel S. (1994). Time-Stable boundary conditions for finite-difference schemes solving hyperbolic systems. Methodology and application to high-order compact schemes. J. Comput. Phys. 111, 220

    Article  MATH  MathSciNet  Google Scholar 

  7. Gustafsson B. (1998). On the implementation of boundary conditions for the method of lines. BIT 38, 293

    Article  MATH  MathSciNet  Google Scholar 

  8. Mattsson K. (2003). Boundary procedures for summation by parts operators. J. Sci. Comput. 18: 133

    Article  MATH  MathSciNet  Google Scholar 

  9. Strand, B. (1996). Ph.D. thesis, Uppsala University, Department of Scientific Computing, Uppsala University. Uppsala, Sweden.

  10. Carpenter M., Nordström J., Gottlieb D. (1999). A Stable and Conservative Interface Treatment of Arbitrary Spatial Accuracy. J. Comput. Phys. 148, 341

    Article  MATH  MathSciNet  Google Scholar 

  11. Nordström J., Carpenter M. (2001). High-order finite difference methods, multidimensional linear problems and curvilinear coordinates. J. Comput. Phys. 173, 149

    Article  MATH  MathSciNet  Google Scholar 

  12. Reula, O. (1998). Living Rev. Rel. 1, 3. URL http://relativity.livingreviews.org/Articles/ lrr-1998-3/index.html.

  13. Rauch J. (1985). Symmetric positive systems with boundary characteristics of constant multiplicity. Trans. Am. Math. Soc. 291, 167

    Article  MATH  MathSciNet  Google Scholar 

  14. Secchi P. (1996). The initial boundary value problem for linear symmetric hyperbolic systems with characteristic boundary of constant multiplicity. Differential Integral Equations 9, 671

    MATH  MathSciNet  Google Scholar 

  15. Secchi P. (1996). Well-posedness of characteristic symmetric hyperbolic systems. Arch. Rat. Mech. Anal. 134, 155

    Article  MATH  MathSciNet  Google Scholar 

  16. Lehner, L., Reula, O., and Tiglio, M. (2005). Multi-block simulations in general relativity: high order discretizations, numerical stability, and applications. Class. Quantum Grav. 22 gr-qc/0507004.

  17. Strand B. (1994). Summation by parts for finite differencing approximations for d/dx. J. Comput. Phys. 110, 47

    Article  MATH  MathSciNet  Google Scholar 

  18. Svärd M., Mattsson K., Nordström J. (2005). Steady State Computations Using Summation by Parts Operators. J. Sci. Comput. 24, 79

    Article  MATH  MathSciNet  Google Scholar 

  19. Mattsson K., Svärd M., Nordström J. (2004). Stable and accurate artificial dissipation. J. Sci. Comput. 21, 57

    Article  MATH  MathSciNet  Google Scholar 

  20. Friedrich, H. (2002). Conformal Einstein evolution. Lect. Notes Phys. 604, 1, gr-qc/0209018.

  21. Tadmor, E. (1994). Spectral methods for hyperbolic problems. In Lecture notes delivered at Ecole des Ondes, "Méthodes numériques d’ordre élevé pour les ondes en régime transitoire", INRIA–Rocquencourt January 24-28. URL http://www.cscamm.umd.edu/people/faculty/tadmor/pub/spectral-approximations/Tadmor.INRIA-94.pdf.

  22. Svärd M. (2004). On coordinate transformations for summation-by-parts operators. J. Sci. Comput. 20, 1

    Article  MathSciNet  Google Scholar 

  23. Zink, B., Diener, P., Pazos, E., and Tiglio, M. (2006). Cauchy-perturbative matching reexamined: Tests in spherical symmetry. Phys. Rev. D 73, 084011, gr-gc/0511163.

  24. Goodale, T., Allen, G., Lanfermann, G., Massó, J., Radke, T., Seidel, E., and Shalf, J. (2003). The cactus framework and toolkit: Design and applications. In Vector and Parallel Processing – VECPAR’2002, 5th International Conference, Lecture Notes in Computer Science, Springer, Berlin. URL http://www.cactuscode.org/Publications/

  25. Cactus Computational Toolkit home page, URL http://www.cactuscode.org/

  26. Schnetter E., Hawley S.H., Hawke I. (2004). Evolutions in 3D numerical relativity using fixed mesh refinement. Class. Quantum Grav. 21: 1465, qc/0310042

    Article  MATH  MathSciNet  Google Scholar 

  27. Mesh Refinement with Carpet, URL http://www.carpetcode.org/.

  28. Schnetter E., Diener P., Dorband N., Tiglio M. (2006). A multi-block infrastructure for three-dimensional time-dependent numerical relativity. Class. Quantum Grav. 23, S 553 gr-qc/0602104

    Article  MathSciNet  Google Scholar 

  29. LAPACK: Linear Algebra Package, URL http://www.netlib.org/lapack/.

  30. BLAS: Basic Linear Algebra Subroutines, URL http://www.netlib.org/blas/.

  31. Netlib Repository, URL http://www.netlib.org/.

  32. Burns, G., Daoud, R., and Vaigl, J. (1994). LAM: An Open Cluster Environment for MPI. In Proceedings of Supercomputing Symposium, pp. 379–386, URL http://www.lam-mpi.org/download/files/lam-papers.tar.gz.

  33. Squyres, J. M., and Lumsdaine, A. (2003). A Component Architecture for LAM/MPI. In Proceedings, 10th European PVM/MPI Users’ Group Meeting (Springer-Verlag, Venice, Italy, 2003), no. 2840 in Lecture Notes in Computer Science, pp. 379–387.

  34. LAM: LAM/MPI Parallel Computing, URL http://www.lam-mpi.org/

  35. Gropp W., Lusk E., Doss N., Skjellum A. (1996). A high-performance, portable implementation of the MPI message passing interface standard. Parallel Computing 22, 789

    Article  MATH  Google Scholar 

  36. Gropp, W. D., and Lusk, E. (1996). User’s Guide for mpich, a Portable Implementation of MPI, Mathematics and Computer Science Division, Argonne National Laboratory, ANL-96/6.

  37. MPICH: ANL/MSU MPI implementation, URL http://www-unix.mcs.anl.gov/mpi/ mpich/.

  38. MPI: Message Passing Interface Forum, URL http://www.mpi-forum.org/.

  39. Sonderforschungsbereich/Transregio 7 “Gravitational Wave Astronomy”, URL http://www.tpi. uni-jena.de/SFB/.

  40. CCT Numerical Relativity, URL http://www.cct.lsu.edu/about/focus/numerical/

Download references

Author information

Authors and Affiliations

  1. Department of Physics and Astronomy, Louisiana State University, 202 Nicholson Hall, Baton Rouge, LA, 70803, USA

    Peter Diener, Ernst Nils Dorband & Manuel Tiglio

  2. Center for Computation and Technology, Louisiana State University, 302 Johnston Hall, Baton Rouge, LA, 70803, USA

    Peter Diener, Ernst Nils Dorband, Erik Schnetter & Manuel Tiglio

  3. Max-Planck-Institut für Gravitationsphysik, Albert-Einstein-Institut, Am Mühlenberg 1, D-14476, Golm, Germany

    Erik Schnetter

Authors
  1. Peter Diener
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ernst Nils Dorband
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Erik Schnetter
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Manuel Tiglio
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Manuel Tiglio.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Diener, P., Dorband, E.N., Schnetter, E. et al. Optimized High-Order Derivative and Dissipation Operators Satisfying Summation by Parts, and Applications in Three-dimensional Multi-block Evolutions. J Sci Comput 32, 109–145 (2007). https://doi.org/10.1007/s10915-006-9123-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-006-9123-7

Keywords

Search

Navigation