Skip to main content
SpringerLink
Log in

Padé-Legendre Interpolants for Gibbs Reconstruction

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

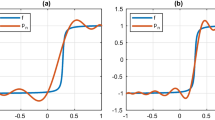
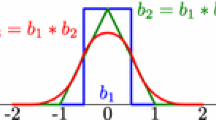
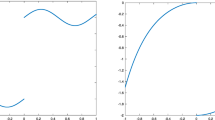
We discuss the use of Padé-Legendre interpolants as an approach for the postprocessing of data contaminated by Gibbs oscillations. A fast interpolation based reconstruction is proposed and its excellent performance illustrated on several problems. Almost non-oscillatory behavior is shown without knowledge of the position of discontinuities. Then we consider the performance for computational data obtained from nontrivial tests, revealing some sensitivity to noisy data. A domain decomposition approach is proposed as a partial resolution to this and illustrated with examples.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bauer, R. (1995). Band Filters for determining shock locations, Ph.D. Thesis, Applied Mathematics, Brown University.

  2. Bernardi, C., and Maday, Y. (1997). Spectral methods. In Handbook of Numerical Analysis V, North-Holland.

  3. Boyd J.P. (2005). Trouble with Gegenbauer reconstruction for defeating Gibbs’ phenomenon: Runge phenomenon in the diagonal limit of Gegenbauer polynomial approximations. J. Comput. Phys. 204(1): 253–264

    Article  MATH  MathSciNet  ADS  Google Scholar 

  4. Don W.S. (1994). Numerical study of pseudospectral methods in shock wave applications. J. Comput. Phys. 110, 103–111

    Article  CAS  MATH  ADS  Google Scholar 

  5. Don W.S., Kaber, S. M., and Min, M. S. (2004). Fourier-Padé Approximations and Filtering for the Spectral Simulations of Incompressible Boussinesq Convection Problem, Accepted for publications in Mathematics of Computation.

  6. Driscoll T.A., Fornberg B. (2001). A Padé-based algorithm for overcoming the Gibbs phenomenon. Numeric. Algorithm. 26, 77–92

    Article  MATH  MathSciNet  Google Scholar 

  7. Emmel, L. (1998). Méthode spectrale multidomaine de viscosité évanescente pour des problèmes hyperboliques non linéaires, Ph.D dissertation, University of Paris 6.

  8. Emmel L., Kaber S.M., Maday Y. (2003). Padé-Jacobi filtering for spectral approximations of discontinuous solutions. Numeric. Algorithm. 33, 251–264

    Article  MATH  MathSciNet  Google Scholar 

  9. Geer J.F. (1995). Rational trigonometric approximations using Fourier series partial sums. J. Sci. Comput. 10, 325–356

    Article  MATH  MathSciNet  Google Scholar 

  10. Gelb A. (2004). Parameter Optimization and reduction of round off Error for the Gegenbauer reconstruction method. J. Sci. Comput. 20, 433–459

    Article  MATH  MathSciNet  Google Scholar 

  11. Gelb A., Tadmor E. (1999). Edge detection from spectral data. Appl. Harmonic Anal. 7, 101–135

    Article  MATH  MathSciNet  Google Scholar 

  12. Gelb A., Tadmor E. (2000). Detection of edges in spectral data II. Nonlinear enhancement. SINUM 38, 1389–1408

    MATH  MathSciNet  Google Scholar 

  13. Gottlieb D., Shu C.W. (1997). On the Gibbs phenomenon and its resolution. SIAM Rev. 39, 644–668

    Article  MATH  MathSciNet  Google Scholar 

  14. Gottlieb, D., and Tadmor, E. (1984). Recovering pointwise values of discontinuous data with spectral accuracy, In Progress and Supercomputing in Computational Fluid Dynamics. Birkhäuser, Boston, pp. 357–375.

  15. Gottlieb D., Hesthaven J.S. (2001). Spectral methods for hyperbolic equations. J. Comput. Appl. Math. 128, 83–131

    Article  MATH  MathSciNet  Google Scholar 

  16. Hesthaven J. S., and Kirby, M. (2005). Filtering in Legendre spectral methods, (submitted).

  17. Hesthaven, J. S., and Kaber, S. M. (2005) Padé-Jacobi approximants. (submitted).

  18. Kaber, S. M. and Vandeven, H. (1993). Reconstruction d’une fonction discontinue á partir de ses coefficients de Legendre, C.R.A.S. 317, série I.

  19. Kaber S.M., Maday Y. (2004). Analysis of some Padé-Chebyshev approximants. SIAM J. Numer. Anal. 43, 437–454

    Article  MathSciNet  Google Scholar 

  20. Matos A.C. (2001). Recursive computation of Padé-Legendre approximants and some acceleration properties. Numer. Math. 89, 535–560

    Article  MATH  MathSciNet  ADS  Google Scholar 

  21. Tanner J., Tadmor E. (2002). Adaptive mollifiers – high resolution recover of piecewise smooth data from its spectral information. Found. Comput. Math. 2, 155–189

    MATH  MathSciNet  Google Scholar 

  22. Vandeven H. (1991). Family of spectral filters for discontinuous problems. J. Sci. Comput. 8, 159–192

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Division of Applied Mathematics, Brown University, Box F, Providence, RI, 02912, USA

    J. S. Hesthaven & L. Lurati

  2. Laboratoire Jacques-Louis Lions, Université Pierre & Marie Curie, 75252, Paris cedex 05, France

    S. M. Kaber

Authors
  1. J. S. Hesthaven
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. M. Kaber
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. L. Lurati
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to J. S. Hesthaven.

Additional information

Dedicated to our friend and mentor, Prof David Gottlieb, on the occasion of his 60th birthday

Rights and permissions

Reprints and permissions

About this article

Cite this article

Hesthaven, J.S., Kaber, S.M. & Lurati, L. Padé-Legendre Interpolants for Gibbs Reconstruction. J Sci Comput 28, 337–359 (2006). https://doi.org/10.1007/s10915-006-9085-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-006-9085-9

Keywords

Search

Navigation