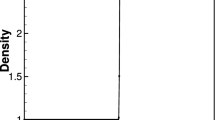
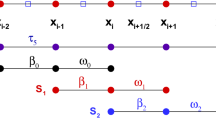
In this note we consider the application of the WENO scheme to simulations of steady-state flow in a converging diverging nozzle. We demonstrate the recovery of design accuracy through Gegenbauer postprocessing, despite the degradation of the order of accuracy for the numerical solution of the Euler equations to first-order in regions where the characteristics passed through the shock. We have shown a case in which the Gegenbauer postprocessing can recover the order of accuracy right up to the shock location. This suggests that high-order accurate information which crosses through the shock may not be irretrievably lost, and we can strive to recover it through various types of postprocessing.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Archibald R., Gelb A., and Yoon J. (2005). Polynomial fitting for edge detection in irregularly sampled signals and images. SIAM J. Numer. Anal 43:259–279
Bateman H. (1953). Higher Transcendental Functions, Vol 2. McGraw-Hill, New York
Casper J., and Carpenter M. (1998). Computational considerations for the simulation of shock induced sound. SIAM J. Sci. Comput 19:813–828
Gelb A. (2004). Parameter optimization and reduction of round off error for the Gegenbauer reconstruction method. J. Sci. Comput 20:433–459
Gelb A., and Tadmor E. (2000). Enhanced spectral viscosity approximations for conservation laws. Appl. Numer. Math. 33: 3–21
Gottlieb D., Shu C.-W., Solomonoff A., and Vandeven H. (1992). On the Gibbs phenomenon I: recovering exponential accuracy from the Fourier partial sum of a non-periodic analytic function. J. Comput. Appl. Math 43:81–98
Gottlieb D., and Shu C.-W. (1996). On the Gibbs phenomenon III: recovering exponential accuracy in a sub-interval from a spectral partial sum of a piecewise analytic function. SIAM J. Numer. Anal 33:280–290
Gottlieb D., and Shu C.-W. (1995). On the Gibbs phenomenon IV: recovering exponential accuracy in a sub-interval from a Gegenbauer partial sum of a piecewise analytic function. Math. Comput 64:1081–1095
Gottlieb D., and Shu C.-W. (1995). On the Gibbs phenomenon V: recovering exponential accuracy from collocation point values of a piecewise analytic function. Numerische Mathematik 71:511–526
Gottlieb D., and Shu C.-W. (1997). On the Gibbs phenomenon and its resolution. SIAM Rev 30:644–668
Harten A., Engquist B., Osher S., and Chakravarthy S. (1987). Uniformly high order essentially non-oscillatory schemes I. SIAM J. Numer. Anal 24:279–309
Harten A., Engquist B., Osher S., and Chakravarthy S. (1987). Uniformly high order essentially non-oscillatory schemes III. J. Comput. Phys 71:231–303
Jiang G.-S., and Shu C.-W. (1996). Efficient implementation of weighted ENO schemes. J. Comput. Phys 126:202–228
Lax P.D. (1978). Accuracy and resolution in the computation of solutions of linear and nonlinear equations. In: De Boor C., and Golub G. (eds). Recent Advances in Numerical Analysis. Academic Press, New York
Lax P., and Mock M. (1978). The computation of discontinuous solutions of linear hyperbolic equations. Commun. Pure Appl. Math 31:423–430
Liu X-D., Osher S., and Chan T. (1994). Weighted essentially non-oscillatory schemes. J. Comput. Phys 115:200–212
Majda A., and Osher S. (1977). Propagation of error into regions of smoothness for accurate difference approximations to hyperbolic equations. Commun. Pure Appl. Math. 30: 671–705
Shu C.-W., and Osher S. (1988). Efficient implementation of essentially non-oscillatory shock-capturing schemes. J. Comput. Phys 77:439–471
Shu C.-W., and Wong P. (1995). A note on the accuracy of spectral method applied to nonlinear conservation laws. J. Sci. Comput 10:357–369
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Gottlieb, S., Gottlieb, D. & Shu, CW. Recovering High-Order Accuracy in WENO Computations of Steady-State Hyperbolic Systems. J Sci Comput 28, 307–318 (2006). https://doi.org/10.1007/s10915-006-9078-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-006-9078-8