Abstract
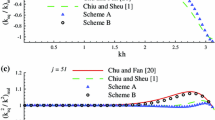
Compact difference schemes have been investigated for their ability to capture discontinuities. A new proposed scheme (Sengupta, Ganerwal and De (2003). J. Comp. Phys. 192(2), 677.) is compared with another from the literature Zhong (1998). J. Comp. Phys. 144, 622 that was developed for hypersonic transitional flows for their property related to spectral resolution and numerical stability. Solution of the linear convection equation is obtained that requires capturing discontinuities. We have also studied the performance of the new scheme in capturing discontinuous solution for the Burgers equation. A very simple but an effective method is proposed here in early diagnosis for evanescent discontinuities. At the discontinuity, we switch to a third order one-sided stencil, thereby retaining the high accuracy of solution. This produces solution with vastly reduced Gibbs' phenomenon of the solution. The essential causes behind Gibbs' phenomenon is also explained.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
REFERENCES
Lele S. K. (1992). Compact finite difference schemes with spectral like resolution. J. Comp. Phys. 103, 16–42.
Haras Z., and Ta 'asan S. (1994). Finite difference schemes for long-time integration. J. Comput. Phys. 114, 265–279.
Adams N. A., and Shariff K. (1996). A high resolution hybrid compact-ENO scheme for shock-turbulence interaction problems. J. Comp. Phys. 127, 27–51.
Zhong X. (1998). High order nite difference schemes for numerical simulation of hypersonic boundary layer transition. J. Comp. Phys. 144, 622–709.
Sengupta T. K., Ganerwal G., and De S. (2003). Analysis of central and compact schemes. J. Comp. Phys. 192(2), 677–694.
Tam C. K. W., and Webb J. C. (1993). Dispersion-relation-preserving nite difference schemes for computational acoustics. J. Comp. Phys. 107, 262–281.
Lighthill M. J. (1978). Waves in Fluids, Cambridge University Press, U. K.
Sengupta T. K., Sridar D., Sarkar S., and De S. (2001). Spectral analysis of ux vector splitting nite volume methods. Int. J. Numer. Meth. Fluids. 37, 149–174.
Jiang G. S and Shu C.-W. Efficient implementation of weighted ENO schemes. J. Comp. Phys. 126, 202.
Pirozzoli S. (2002). Conservative hybrid compact-WENO scheme for shock-turbulence interaction. J. Comp. Phys. 178, 81–117.
van Leer B. (1974). Towards the ultimate conservative difference scheme. II. Monotonicity and conservation combined in a second-order scheme. J. Comp. Phys. 14, 361–370.
Roe P. L., and Baines M. J. (1982). Algorithms for advection and shock problems. In the Proc. of 4th GAMM Conf. on Numerical Methods in Fluid Mechanics. Vieweg, Braunschweig.
Roe P. L. (1985). Some contribution to the modelling of discontinuous flows. Lectures in Applied Mathematics, 22, 163–193.
van Leer B. (1979). Towards the ultimate conservative difference scheme. V. A second order sequel to Godunov 's method. J. Comp. Phys. 32, 101–136.
Koren B. (1993). A robust upwind discretization method for advection, diffusion and source term. In Numerical Methods for Advection-Diffusion Problems (C. B. Vreugdenhil and B. Koren, eds. ), Vieweg, braunschweig. pp. 117–137.
Sengupta T. K., Anuradha G., and De S. (2003). Incompressible Navier-Stokes solution by new compact schemes. In Proc. of 2nd MIT Conf. on Comp. Fluid and Solid Mech. (K. J. Bathe, ed., ).
Lax P. D., and Wendroff B. (1960). Systems of conservation laws. Comm. Pure Appl. Math. 13, 217–237.
Harten A., Engquist B., Osher S., and Chakravarthy S. (1987). Uniformly high order essentially non oscillatory schemes III. J. Comp. Phys. 71, 213.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Sengupta, T.K., Ganerwal, G. & Dipankar, A. High Accuracy Compact Schemes and Gibbs' Phenomenon. Journal of Scientific Computing 21, 253–268 (2004). https://doi.org/10.1007/s10915-004-1317-2
Issue Date:
DOI: https://doi.org/10.1007/s10915-004-1317-2