Introduction

A wide range of properties of polycrystalline materials is influenced by intergranular boundaries. The most basic attribute of a boundary is its "macroscopic" geometry, which can be described by a misorientation between neighboring grains and boundary plane indices, i.e., by five independent parameters [1]. A thorough understanding of macroscopic features of boundaries is essential for more comprehensive boundary studies at the atomic scale. Thanks to recent advances in development of both destructive (e.g., [2]) and nondestructive (e.g., [3]) three-dimensional techniques of microstructure imaging, the five macroscopic parameters of significant numbers of boundaries are experimentally accessible. The large sizes of boundary data sets open new possibilities for carrying out statistical analyses of boundary networks. In particular, distributions of grain boundaries with respect to their macroscopic parameters are studied (e.g., [4–6]). These distributions indicate which boundary geometries are preferred, and which are underrepresented. The question arises whether maxima in the distributions correspond to boundaries of special geometries, e.g., to twist, tilt, or symmetric boundaries. To answer it, the boundaries having characteristic geometries need to be properly identified. In the presence of crystal symmetries, every geometric configuration may have multiple equivalent representations; it is crucial to take them all into consideration to recognize boundary types correctly.

All twist and tilt boundaries of low-Sigma misorientations for the cubic O h symmetry were cataloged in [7]; for each of these misorientations, the catalogs of twist and tilt boundaries were presented in the form of two-dimensional maps containing stereographic projections of the corresponding boundary plane normals. With this representation, the obtained diagrams can be directly linked to the experimental distributions, which are usually displayed in a similar way, i.e., as functions of boundary planes for fixed misorientations. These maps were afterward completed with symmetric and 180°-tilt boundaries in [8].

Since distributions of boundaries in hexagonal materials are also of interest (e.g., [5, 6]), the purpose of this article is to extend the previous studies and to provide analogous patterns for materials of hexagonal D 6h symmetry. Differently than in the cubic case, the resulting figures depend on lattice parameters. We consider the cases of \(c/a=\sqrt{5/2}\) and \(c/a=\sqrt{20/21}\). These ratios correspond, respectively, to α-phase titanium and tungsten carbide. Diagrams containing all twist, tilt, symmetric, and 180°-tilt boundaries for selected misorientations are presented below. The diagrams have been obtained using two complementary approaches: analytical and numerical. The first method allows for immediate determination of exact locations of boundaries of characteristic geometry. However, in practice, experimental errors must be taken into account. The second approach provides all boundaries that satisfy type-defining conditions with assumed tolerance thresholds; it utilizes certain parameters introduced recently [9] to approximate the distances (defined in the space of boundary parameters [10–12]) to the nearest twist, tilt, symmetric, and 180°-tilt boundaries. The costs of computing these parameters are low, and therefore, the diagrams are obtained more effectively compared to the time-consuming accurate calculation of the distances used in [7].

To demonstrate the usefulness of our patterns and to indicate issues related to interpretation of the experimental distributions, some of the obtained diagrams are compared to example sections through experimental distributions of grain boundaries in Ti alloy published in [6] and WC/WC boundaries in WC–Co composites presented in [5]; the peaks reported in the sections through the distribution of WC/WC boundaries are characterized in a systematic way.

Methods

Analytical calculations

In the case of D 6h symmetry, geometry of a boundary is fully described by a misorientation M and Miller-Bravais indices (h 1 k 1 i 1 l 1) of the boundary plane expressed in the reference frame of the first grain [11]. The indices of that plane given in the frame attached to the second grain are \((h_{2} k_{2} i_{2} l_{2}) = M^{-1} {\circ} (\bar{h}_{1} \bar{k}_{1} \bar{i}_{1} \bar{l}_{1})\), where the sign “\({\circ}\)” denotes a rotation of a crystallographic plane. The same boundary can also be represented by \((h'_{1} k'_{1} i'_{1} l'_{1}) = C_{1} {\circ} (h_{1} k_{1} i_{1} l_{1})\), the corresponding \((h'_{2} k'_{2} i'_{2} l'_{2}) = C_{2} {\circ} (h_{2} k_{2} i_{2} l_{2})\) with C 1 and C 2 being proper symmetry rotations of the considered point group applied to the first and second grains, respectively, and by equivalent misorientation \(M' = C_{1} {\circ} M {\circ} C_{2}^{-1}\) (here, “\({\circ}\)” stands for compositions of rotations). Due to inversion symmetry, the representation by M and (h 1 k 1 i 1 l 1) is equivalent to that by M and \((\bar{h}_{1} \bar{k}_{1} \bar{i}_{1} \bar{l}_1)\). Additionally, for homo-phase boundaries, grain exchange symmetry implies that also the pair M −1 and (h 2 k 2 i 2 l 2) describes the same boundary. Hence, for D 6h symmetry, there are up to 2 × 2 × 12 × 12 different equivalent grain boundary representations in the complete domain of the macroscopic parameters.

A boundary is referred to as a twist boundary if it has a representation with the misorientation axis perpendicular to the boundary plane, while for a tilt boundary, there exists a description with the axis lying in that plane. Symmetric boundaries can also be represented as 180°-twist boundaries; 180°-tilt boundaries are sometimes called improperly quasi-symmetric [13].

Grain boundaries will not be classified correctly unless equivalent representations are processed. It is not enough to limit the analysis to representations with disorientations, because many of the characteristic boundaries will be overlooked. For instance, a boundary in a material with \(c/a\approx\sqrt{5/2}\) described by the \(\Upsigma 11b\) misorientation [14], i.e., 84.78° rotation about the \([2\bar{1}\bar{1}0]\) axis (denoted by \(84.78^{\circ}/[2\bar{1}\bar{1}0]\)), and the \((0\bar{1}12)\) plane is visibly a tilt boundary, but its 180°-twist and 180°-tilt characters are not directly apparent. However, this boundary can also be represented by the \(180^{\circ}/[01\bar{1}\bar{1}]\) misorientation and \((0\bar{1}1\bar{2})\) plane; thus, the boundary is indeed a 180°-tilt. Other equivalent parameters of this boundary are the \(180^{\circ}/[0\bar{5}5\bar{6}]\) misorientation and \((01\bar{1}2)\) plane; since the normal to the \((01\bar{1}2)\) boundary plane is \([05\bar{5}6]\), the boundary has also a twist character.

The simplest algorithm for finding all boundaries of characteristic geometry is based on analytical derivations. First, one applies symmetry transformations C 1 and C 2 to a fixed misorientation M to get its equivalent representations M′. Then, based on the aforementioned type definitions, all planes of characteristic boundaries can be determined from the corresponding misorientation axes. Finally, by transforming the indices of these planes to the initial reference frame using inverse transformations C −11 and C −12 , one obtains the boundary normals to be included in a diagram. For instance, application of the transformations \(C_{1} = 180^{\circ}/[\bar{1}2\bar{1}0]\) and C 2 = identity to the misorientation \(M = 84.78^{\circ}/[2\bar{1}\bar{1}0]\) (\(\Upsigma 11b\)) gives \(M' = 180^{\circ}/[0\bar{5}5\bar{6}]\). For this equivalent misorientation, boundaries with the planes \((01\bar{1}2)\) and \((0\bar{1}1\bar{2})\) (with the normals \([0\bar{5}5\bar{6}]\) and \([05\bar{5}6]\), respectively) have explicit twist characters, and there is a zone of planes parallel to the misorientation axis, i.e., corresponding explicitly to tilts. Since the misorientation is a half-turn, these twist and tilt boundaries are also symmetric and 180°-tilt boundaries, respectively. The indices of these planes need to be transformed to the initial reference frame, e.g., \(C_1^{-1}{\circ}(01\bar{1}2) = (0\bar{1}12)\). Proceeding in an analogous manner with all misorientation representations, one finds all boundaries of characteristic geometry.

Numerical searches

Measured boundary parameters are affected by the experimental errors. The resolution for determination of boundary plane inclinations is relatively poor. For an apparatus combining electron backscatter diffraction and serial sectioning, it has been estimated to be about 7.5° [4]. Hence, it is difficult to match the measured parameters to the definitions of characteristic boundary types. Therefore, relying on patterns containing only exact locations of the boundaries of characteristic geometry (without any tolerance) is insufficient for interpretation of the boundary distributions.

With error-affected data, it is more suitable to identify boundary types using metric functions defined in the boundary space: if the distance from a given boundary to the nearest twist, tilt, or symmetric boundary is below an assumed threshold, then the boundary is classified as near-twist, near-tilt, or near-symmetric, respectively.

The distributions of these distances for fixed misorientations and varying boundary planes (displayed as two-dimensional contour graphs on stereographic projections, cf. [7]) may serve as patterns useful in analyses of grain boundary distributions. The patterns of this kind have the advantage in taking into account experimental uncertainties: the zero values clearly correspond to pure-twist, pure-tilt, or pure-symmetric boundaries, and the isolines corresponding to assumed tolerance thresholds surround all near-twist, near-tilt, or near-symmetric boundaries of given misorientations.

To obtain detailed diagrams for fixed misorientations, the values of the distances need to be probed at densely distributed boundary normals. Since calculation of the distances involves complex numerical algorithms [7], the times needed for obtaining the maps become long. This difficulty is circumvented by substituting the properly defined distances to the nearest twist, tilt, symmetric, and 180°-tilt boundaries by recently suggested approximating parameters [9]. These parameters are strongly correlated with the corresponding distances, so they provide similar characteristics of a given boundary, and they can be computed significantly faster than the distances. The times needed for computing the approximated maps are about three orders of magnitude shorter than those for the maps with the accurate distances.

Diagrams with characteristic boundaries

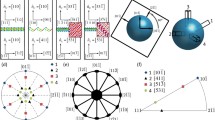
Example diagrams obtained using the analytical method for the c/a ratio at \(\sqrt{5/2}\) and the \(\Upsigma 11b\) and \(\Upsigma 19a\) (\(65.10^{\circ}/[10,\bar{5},\bar{5},3]\)) misorientations are presented in Fig. 1a, b. In these maps, twist boundaries and zones of tilt boundaries are represented by, respectively, points and lines. Symmetric boundaries being particular twist boundaries have less degrees of freedom, and in consequence, they occur less frequently than twists; similarly, 180°-tilts are less frequent than tilts (cf. [15]). E.g., for the \(\Upsigma 19a\) misorientation (Fig. 1b), among ten distinct twist boundaries and the ten corresponding tilt zones, there is only one symmetric boundary and one 180°-tilt zone.

Fig. 1
figure 1

Stereographic projections of poles of boundary planes corresponding to twist (points), tilt (thin lines), symmetric (circles), and 180°-tilt (thick lines) grain boundaries of the \(\Upsigma 11b\) (a) and \(\Upsigma 19a\) (b) misorientations and for \(c/a = \sqrt{5/2}\); symmetries of boundary-plane distributions for these misorientations are shown in (c) and (d), respectively

Full size image

Using the diagrams, one can identify boundaries with characteristic geometries. By this, we mean boundaries lying at the intersections of multiple tilt zones and boundaries ascribed to more than one type, e.g., \(\Upsigma 11b\) boundaries with \((1\bar{1}12)\) and \((03\bar{3}5)\) planes (Fig. 1a). Boundaries with multiple tilt axes must be two-dimensionally periodic; such ordered structures may have uncommon properties, especially if the tilt axes are low-index, i.e., if the periodically repeated cell is small. Boundaries being simultaneously of more than one type can be expected to have specific geometries, and therefore, they may also have special properties.

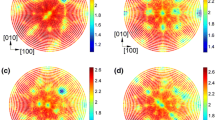
Example diagrams computed using the numerical approach, that is, the distributions of the approximated distances to the nearest characteristic boundaries for \(c/a=\sqrt{20/21}\) and for the \(90^{\circ}/[10\bar{1}0]\) and 30°/[0001] misorientations are plotted in Figs. 2 and 3. For a given tolerance threshold, near-twist and near-tilt boundaries are represented by spots and bands, respectively. The figures are compared to the sections through experimental distribution of WC/WC grain boundaries in WC–Co composites described in [5].

Fig. 2
figure 2

Experimental distribution of planes of WC/WC boundaries for the \(90^{\circ}/[10\bar{1}0]\) misorientation (a) reprinted from [5], with permission from John Wiley & Sons; its symmetries are shown in (b). The corresponding distributions (for \(c/a = \sqrt{20/21}\)) of the approximated distances (in degrees) to the nearest twist (c), tilt (d), symmetric (e), and 180°-tilt (f) boundaries. The distributions are given as functions of boundary plane normals and plotted on stereographic projections. Locations of the peaks visible in (a) are marked in (c–f) with white disks

Full size image
Fig. 3
figure 3

Section through experimental distribution of WC/WC boundaries for the 30°/[0001] misorientation (a) reprinted from [5], with permission from John Wiley & Sons; its symmetries are shown in (b). The related distributions (for \(c/a = \sqrt{20/21}\)) of the approximated distances (in degrees) to the nearest twist (c), tilt (d), symmetric (e), and 180°-tilt (f) boundaries. The distributions are given as functions of boundary planes and are displayed on stereographic projections. Locations of the peaks visible in (a) are marked in (c–f) with white disks

Full size image

Discussion

Similarly to the cubic case, the diagrams obtained for hexagonal symmetry reveal a variety of boundaries of characteristic geometry. Depending on the misorientation, the diagrams may exhibit some symmetries (cf. [16]), and not all of the identified characteristic boundaries correspond to macroscopically different configurations. There are groups of twist and tilt boundaries the planes of which belong to the same plane families. The symmetries in the boundary-plane distributions for a given misorientation follow from analysis of equivalent boundary representations analogous to that in the example in "Analytical calculations" section. The symmetries for the considered misorientations are shown in Figs. 1c, d, 2b, 3b.

The diagrams in Fig. 1 can be directly used to characterize the extrema occurring in the experimental distributions of boundaries in the Ti alloy presented in [6]. Let us focus on the diagram for the \(\Upsigma 19a\) misorientation (Fig. 1b) corresponding to the section through the experimental distribution (Fig. 4 of [6]). The peaks visible in that section were interpreted as corresponding to the \((4\bar{1}\bar{3}0)\) and \((\bar{4}130)\) boundary planes. With the tolerance of <3°, the \(\{4\bar{1}\bar{3}0\}\) planes are indistinguishable from the \(\{3\bar{1}\bar{2}0\}\) planes. Thus, the observed peaks can be interpreted as special boundaries being simultaneously twists and 180°-tilts.

To demonstrate a possible scheme of interpretation of grain boundary distributions using numerically obtained patterns, we will characterize the peaks of the distribution of WC/WC boundaries in WC–Co composites. Let us consider each of the three sections through the distribution shown in Fig. 8 of [5].

  • The section for the \(90^{\circ}/[10\bar{1}0]\) misorientation (see Fig. 2) contains two strong peaks at the \((10\bar{1}0)\) and \((\bar{1}010)\) poles. These are directly related to pure-twist boundaries. With our maps, these two configurations are also recognized as double 180°-tilts. The distances of the peaks to symmetric boundaries are very large.

  • In the case of the 30°/[0001] misorientation (see Fig. 3), there is a maximum for the (0001) plane. These are the twist boundaries. The (0001) plane is also located at the intersection of six 180°-tilt zones. Elevated values of the distribution occurred also at the prismatic positions \((10\bar{1}0)\), \((11\bar{2}0)\). These are tilts, but they are neither twist nor symmetric nor 180°-tilt boundaries.

  • In the distribution of boundary planes for the \(90^{\circ}/[\bar{2}110]\) misorientation, there are peaks at the (0001), \((1\bar{1}00),\) and \((\bar{1}100)\) poles. The distributions of the distances corresponding to this misorientation are almost identical to those for the \(90^{\circ}/[10\bar{1}0]\) misorientation with the only difference that they are rotated clockwise by 30° (therefore, only the latter are shown). The peak for the (0001) plane corresponds to a boundary with a single tilt axis. The other two maxima lie on the intersections of two tilt zones.

All these overrepresented boundaries have at least one tilt axis. Interestingly, none of them can be classified as symmetric. The two highest peaks are interpreted as twist boundaries located at the intersections of 180°-tilt zones. The interpretations of all the maxima are collected in Table 1.

Table 1 Characterization of the peaks in the distribution of WC/WC boundaries in a WC–Co composite
Full size table

Final remarks

Geometrically characteristic boundaries (i.e., twist, tilt, symmetric, and 180°-tilt boundaries) have been identified for selected misorientations between crystals of hexagonal holohedral symmetry with c/a ratios equal to \(\sqrt{5/2}\) and \(\sqrt{20/21}\). The obtained sets of boundaries with characteristic geometry for given misorientations have been presented in the form of diagrams containing stereographic projections of the poles of boundary planes. These diagrams are helpful in interpretation of the experimentally obtained grain boundary distributions. As an example, the peaks occurring in the distribution of WC/WC boundaries of [5] have been systematically characterized. In the distribution of WC/WC boundaries in WC–Co composites, all the reported maxima happen to correspond to either single- or multiple-tilt boundaries, and their geometries are far from symmetric geometry. The two highest peaks are also identified as special boundaries being twist boundaries located at the intersections of multiple 180°-tilt zones.

Grain boundaries are extensively studied using various techniques at different length scales. We believe that more detailed interpretation of boundary distributions may provide important hints for further investigations of both individual boundary types and quantitative studies of boundary networks. This work is focused on hexagonal materials, but the described methods can be applied to boundaries between crystals with other holohedral symmetries.