1 Introduction

The goal of this paper is to combine mathematical methods in the parametrization and least-squares modeling of geophysical data. These complementary methods used to accelerate and automatize precise spatial modeling process are: least-squares collocation (LSC), Fisher scoring (FS) solution of restricted maximum likelihood (REML) and Levenberg–Marquardt optimization (LM). LSC is a parametric method applied in 2D interpolation of gravity in this study. LSC is based on the covariance model and needs parameters, which are provided here by FS solution of REML extremum. FS is optimized by the LM method to resolve convergence problems and to provide robustness to poor initial parameters. A large number of studies with regard to the spatial modeling has shown that a separate use of the abovementioned methods do not solve the assumed goal. LSC is not accurate without REML estimation of the noise variance, whereas FS without optimization has serious problems related to the convergence.

The applicability of REML to the estimation of the parameters in LSC modeling, as well as its accuracy in this application, has been proven in the previous works of the author (Jarmołowski 2013, 2016). Therefore, this study is focused only on an unsolved issue, i.e., the straightforward, fast and robust calculation of REML minimum via FS optimized by LM (FSLM).

1.1 Least-Squares Collocation and Covariance Model Parametrization

At present, in the century of extensive satellite observation of the planets, diverse measurement techniques provide geophysical data applied in the modeling of different phenomena in many dimensions. The basic two are space and time. The literature examples cited hereafter also consider various phenomena mainly in relation to space and time. The problems considered in this article refer to spatial and time correlation of the signal representing physical quantity as well as to the covariance that represents it mathematically. The properly determined covariance of the signal and noise enables stochastic modeling of the signal based on the randomly distributed data. The same data are used to calculate covariance parameters, which are the object of the current investigation. Their accurate estimation is a key problem in parametric techniques of interpolation and extrapolation.

The nonparametric techniques of interpolation and extrapolation are rated as insufficient in geophysics for decades, as they do not use accurate signal covariance models and often do not take data noise into account. Therefore, two parametric spatial domain techniques are almost exclusively considered today, i.e., least-squares collocation (LSC) and kriging. They are even comparable and very closely related if LSC is only an interpolation with no transformation between physical quantities and kriging form is simple kriging (SK). The additional, interesting occurrence is a growing number of LSC applications in various geophysical investigations, which replaces ordinary kriging (OK), more popular in geophysics during former decades (El-Fiky et al. 1997, 1999; Jiang et al. 2014; Kato et al. 1998). Both techniques are based on the covariance models represented by the covariance function or semivariogram. The shape of both covariance model types depends on the estimable parameters, which are characteristic for the individual data sample. Examples include GPS data analyzed in Jiang et al. (2014), who apply parametrized covariance models to the calculation of tectonic stress accumulation rates in the Tibetan Plateau. El-Fiky et al. (1997, 1999) determine covariance parameters of the vertical and horizontal crustal movements, respectively. Andersen and Knudsen (1998) estimate similar parameters in space domain for the satellite altimetry tracks, whereas Sabaka et al. (2010) apply the parameters describing spatiotemporal correlation of equivalent water height estimates from Gravity Recovery and Climate Experiment (GRACE).

An old and very frequent technique of parameters determination used by a significant number of researchers is the empirical covariance function (ECF) or empirical semivariogram (ES), which are estimated from the data. The covariance matrix in the case of least-squares collocation (LSC) describes the correlation of data residuals, which take part in the stochastic process. This matrix can be approximated by some model using its parameters, which are specific to the selected model and data. In the last decades, a typical approach to the parameters selection in LSC was the estimation of ECF and fitting of the analytical model into the graph of empirical covariance (Arabelos and Tscherning 1998; Darbeheshti and Featherstone 2009; Kato et al. 1998; Łyszkowicz 2010; Smith and Milbert 1999). This fit can be attained manually by a manipulation of the parameters or by the least-squares fitting. Such a procedure consists of at least two steps: a time-consuming calculation of the ECF and the fit of analytical model to ECF, which needs plotting and viewing. This estimation and fitting process is laborious, time-consuming and requires manual steps, which can be avoided by using the technique proposed in this article. Furthermore, it has been noticed that the estimation of the noise variance can be difficult or even impossible by ECF, as it is based on the combination of the signal and noise (Arabelos and Tscherning 1998; Jarmołowski 2013, 2016; Rummel et al. 1979; Sadiq et al. 2010).

A very reliable estimation of covariance parameters is cross-validation (CV), because it provides empirical results of their application to the analyzed data (El-Fiky et al. 1997; Jarmołowski 2013). The CV estimates are optimal and take into account all the factors that disturb covariance estimation, e.g., the usage of an imperfect model. The CV estimation of the parameters can be found in several software packages (e.g., ArcGIS Pro, Surfer, Statistica). However, its application is time-consuming and renders it not fully useful for the practitioners, especially if time is a significant factor. Taking into account all the above drawbacks, many geophysicists investigating signal and noise covariance in various processes apply maximum likelihood (ML) or restricted maximum likelihood (REML), sometimes also called “residual.” This work supports practical REML covariance estimation by an extension of one of the fast REML estimation techniques. The aim of the current work is to validate a fast, effective and unfailing method of solving REML, which finds the same global minimum as the one found directly by the negative log-likelihood function (NLLF) calculation. The current work applies REML form in the estimation, whereas many literature examples cited use ML as a starting point. Koch (2007) and Searle et al. (1992) provide a primer on ML and REML and both books describe the differences between these two techniques.

1.2 Maximum Likelihood Estimation of Covariance Parameters in Geophysics

The problem of covariance model parametrization is in fact an adjustment of this model to the actual spatiotemporal data sample, which can be of an arbitrary size and may have different localization. Therefore, these data or data residuals must be used in the process of the parameters identification, but not alone. Some additional hypotheses have to be applied to the data, e.g., a multivariate Gaussian distribution, which is frequently and willingly adapted to geophysical and geodetic problems. This assumption enables the parameters estimation by ML or REML. Both are very handy alternatives for CV and the ECF, as was shown in many literature examples. The estimation of ECF or ES is then unnecessary, bearing in mind that the distribution of the data is assumed as Gaussian. Of course, there exists a potential drawback of this assumption and it has been not analyzed there. Nevertheless, such an assumption is frequent among researchers (Hansen et al. 2010; Kitanidis and Lane 1985; Miller et al. 2014; Zimmermann et al. 2008), and most of the covariance models are indeed a modification of the Gaussian rule of thumb, which efficiently solves a large number of the spatiotemporal problems in practice.

The ML and REML have been already implemented in many geophysical problems. More precisely, all eight associations of the International Union of Geodesy and Geophysics (IUGG) have collected a significant amount of works related to their individual domains. In alphabetical order, one can find examples of ML or REML in cryospheric sciences, which investigate icequakes, ice cover or snow properties (Canassy et al. 2013; Kwasniok 2013; Reuter et al. 2016). The examples in geodesy include horizontal deformations, gravity data modeling or adjustment of the geodetic networks (Grodecki 1999, 2001; Jarmołowski 2016; Kubik 1970; Yu 1996). ML has been used in geomagnetism for paleomagnetic studies, identification of magnetostratigraphic polarity zones and dating of magnetostratigraphic sections (Arason and Levi 2010; Man 2008, 2011). The hydrologic sciences provide the applications related with floods and soil hydraulic properties (Chowdhary and Singh 2010; Hoeksema and Kitanidis 1985; Sveinsson et al. 2003; Tsai and Li 2008; Ye et al. 2004; Zimmermann et al. 2008). The studies of the atmosphere that are consolidated with meteorology in IUGG investigate important or dangerous phenomena in the atmosphere, like, e.g., fluxes of different atmospheric gases (Michalak et al. 2005; Miller et al. 2014; Winiarek et al. 2012; Zupanski et al. 2007). A separate domain in IUGG is the ocean science and ML techniques have been found as helpful also there, in ocean storm studies, sea surface determination and studies on acoustic waves in the water (Bengtsson et al. 2005; Halimi et al. 2015; Thode et al. 2002; Ueno et al. 2010). The seismological society analyzes the parameters of earthquakes by ML (Console and Murru 2001; Herak et al. 2001; Legrand et al. 2012; Segall and Matthews 1997; Segall et al. 2000). The last, eighth, group of geophysicists, according to the IUGG divisions, is volcanologists, who analyze and predict volcanic eruptions, as well as volcanic ash clouds (Bell et al. 2013; Denlinger et al. 2012; Jones et al. 1999). The above studies represent only a certain number of examples among the larger amount of works in geophysics and in other sciences; however, these works indicate a permanent interest in using and optimizing ML and REML.

1.3 The Log-Likelihood Functions and Their Extrema

The solutions of ML and REML are based on the log-likelihood function (LLF) or its’ negative form NLLF and their descriptions can be found in many statistical books (Koch 2007; Searle et al. 1992). The maxima of LLF or minima of NLLF have been found as frequently used in the analysis of numerous geophysical issues. Kwasniok (2013) provides an interesting illustration of LLF use in the 2D approach in glacial climate studies. He presents different levels of noise in ice-core data determinable by the LLF extremum. Arason and Levi (2010), although involving a few numerical techniques of LLF maximum approximation in the paleomagnetic studies, finally verify these estimates by the use of LLF contours. Many of the implemented methods fail in their investigation of two covariance parameters. The methods that work better in their work need some approximation of the parameters, which is inconvenient and limits their wider use. This problem occurs also in the FS and is investigated in the later sections of this paper. An additional example related with magnetism can be found in Man (2011). He extends the investigation in respect to his previously mentioned paper (Man 2008) by a detailed analysis of LLF extrema. His numerical techniques of extremum derivation also find some limitations and the analysis is supported by the plots of LLF. This analysis has been performed to determine two parameters and therefore the plots are 2D, but only partially in space, because one of the parameters has a time unit. The unit of time also composes a parameter in the investigation of the atmospheric pollutants in Winiarek et al. (2012). They estimate two parameters of covariance and validate two techniques of LLF extremum estimation with a direct calculation of its values in the space of desired parameters. The validation shows that the used methods fail in most of the cases. Denlinger et al. (2012) provide another ML application in atmospheric research and also apply the plot of LLF for the assessment of specific parameters necessary in volcanic ash clouds forecasting. The global NLLF minimum is its lowest value in respect to all the analyzed parameters. However, in several geophysical applications the local minima are found as more often applied, as they are less laborious numerically. Such local ML profiles are implemented (sometimes together with 2D plots) in Segall and Matthews (1997) and Segall et al. 2000). These papers present the studies of earthquakes and analyze their various parameters. An additional important issue that can be found in these works is scaling of the parameters, which can often be helpful in ML analyses. Another work related also with the earthquakes is performed by Console and Murru (2001). It is more closely concerned with typical spatial modeling techniques, as it presents the calculation of the parameters required for seismicity horizontal maps by LLF profile analysis. The example of direct NLLF values use in hydrologic research is a study given by Ye et al. (2004). All the works in this paragraph rely principally on the LLF plotting in 1D or 2D and often neglect the accuracy analysis of ML estimation. The example of accuracy assessment of REML estimates for LSC parameters can be found in Jarmołowski (2013, 2016). The technique has been found as sufficient for LSC parametrization and consistency of REML results with CV has been proven.

1.4 Derivative-Based Techniques in Maximum Likelihood Estimation and the Choice of Fisher Scoring

The accuracy of the parameters estimated by ML or REML can be approximated on the basis of the Fisher information matrix, also known as the information matrix (IM), which is also useful in different tasks related with ML and REML. The derivatives of NLLF with respect to the estimated parameters are necessary in the creation of IM (Searle et al. 1992; Pardo-Igúzquiza et al. 2009). The IM is based on the expectation of the Hessian matrix, which is easier to calculate in practice than Hessian (Grodecki 1999; Osborne 1992; Searle et al. 1992). This is the first property that determines computational advantage of FS in relation to the Hessian-based methods. The inverse of IM at last iteration is used to acquire lower bound of accuracy of the vector of parameters, as is shown in Longford (1987) and in hydrologic studies by Kitanidis (1983), Kitanidis and Lane (1985) and Chowdhary and Singh (2010). Tsai and Li (2008) provide an example of groundwater modeling and also use Fisher IM together with different statistical information criteria to provide the bounds of accuracy estimates. The uncertainty of the estimation of surface fluxes of atmospheric trace gases is based on the IM in Michalak et al. (2005). The Hessian provides a basis for derivative-based, iterative estimation techniques solving ML/REML problem, which are jointly called “Newton-like.” Unfortunately, Hessian depends on the observations and many authors conclude that it provides worse convergence than IM in the implementations (Koch 1986; van Loon 2008; Osborne 1992; Sari and Çelebi 2004; Grodecki 1999). The amount of the literature confronting different derivative-based techniques, including FS and “Newton-like” algorithms is considerable. These comparisons, including theoretical and applied in practice can be found in many articles cited in this work (Giordan et al. 2014; Kitanidis and Lane 1985; Koch 1986; Osborne 1992; Searle et al. 1992; Wang 2007). The review of the existing comparisons and initial numerical test explained at the beginning of Sect. 5 were a basis to select solely FS, as the most interesting method for LSC parametrization, since it can provide temperate iteration step and reasonable speed. As there is no detailed analysis of “Newton-like” techniques in this article, their introduction is limited to a few examples. Some geophysical examples listed below do not use the regularization. The next paragraphs, however, provide some optimized examples, but not necessarily related with geophysics. The Gauss–Newton method has been applied by Michalak et al. (2005) in previously mentioned atmospheric research and their approach is not regularized. Sveinsson et al. (2003) also implement non-optimized Newton–Raphson (NR) iteration in the regional frequency analysis of the hydrologic data. Grodecki (1999) and van Loon (2008) also refer to this technique; however, all these works use non-optimized techniques and usually mention the need for initial estimates. The application of initial prior values of parameters enables an efficient estimation in many cases, even with no optimization; nevertheless this is a serious limitation in case of unknown prior values or if the process requires automation (e.g., real-time application).

This work provides a detailed study of another derivative-based technique called Fisher scoring (FS), which is also iterative (Koch 1986; Searle et al. 1992). The method of scoring is usually named as FS after Ronald Fisher. It was extensively investigated theoretically in the second half of the previous century and numerical applications have arisen in different scientific fields. The FS uses IM, based on the expectation of Hessian, unlike NR, and it is often assessed as more robust for poor starting values of the estimated parameters (Grodecki 1999; Searle et al. 1992). A non-regularized FS is the most often applied form in the preliminary case studies on FS applications (Grodecki 2001; Harville 1977; Yu 1996). The applications are not so frequent in the literature and the convergence problems are often found as a limitation of a non-optimized form of FS (Grodecki 1999; Pardo-Igúzquiza 1997). The conclusion about the poor convergence of primary FS or converging at most to the local minima is repeated many times in the literature (Green 1984; Halimi et al. 2015; Kubik 1970; Sari and Çelebi 2004). This work attempts to analyze it in more detail, to make it more efficient and more readily used.

The literature review shows that direct analyses of NLLF local and global minima are still willingly applied, instead of derivative-based techniques suffering from the problems with convergence of the iterations. The number of ML and REML applications to field data sets including hundreds of points is limited, due to the convergence problems and time-consumption issues related with the estimation, which in case of ML and REML are only partially resolved. Therefore, some researchers expand FS algorithm by applying various conditions or additional components to overcome the problem of convergence (Ahn et al. 2012; Osborne 1992; Sari and Çelebi 2004). Among different ML and REML estimation methods, many include various constraints and approximations (Moghtased-Azar et al. 2014; Wang 2007), whereas others have nested optimization techniques, which enhance their performance (Harville 2004). The Monte Carlo technique is also very popular in solving REML or variance component problems (Han and Xu 2008; Kusche 2003; Wang 2010). All these modifications aim mainly at strengthening the convergence, but not always take time issue into account. A further important factor that has an influence on the convergence is the shape of the function, the minimum of which is required. The NLLF surface in this study is also specific, and it is probable that every individual shape results in a different performance of FS (McKeown and Sprevak 1989).

1.5 Levenberg–Marquardt Optimization in FS and Its Application

The goal of this paper is to analyze numerically the LM optimization of FS (FSLM) in detail, by solving a typical geodetic task, i.e., parametrization of LSC of gravity anomalies. The proposed method is an application of FSLM of the parameters of planar covariance model. Smyth (2002a) proposes this less complicated, fast and potentially efficient FS in the sense of good convergence, i.e., LM optimization, also known as LM damping. This technique is in slightly different context also available in Sari (2006), with additional applications to image processing. In mathematics and computing, the LM, also known as the damped least-squares method, is used to solve nonlinear least-squares problems. The algorithm was first published by K. Levenberg and then rediscovered by Marquardt (1963). LM has been applied numerous times in least-squares problems that are close to FS, e.g., “Newton-like” methods (Fan and Pan 2009; Giordan et al. 2014; Ling et al. 2014; More 1977; Shan 2008; Yang 2013). I follow Smyth (2002a) in this paper and apply FSLM in the estimation of two covariance parameters that are essential in 2D modeling of physical phenomena using planar covariance models. The intentionally selected geodetic example of gravity anomalies depicts a useful application of FSLM. The obtained results can be representative and handy for many planar covariance models of the signal combined with homogeneous, non-correlated noise case. As a matter of fact, the method can be efficient for all covariance models appearing in the works cited in Sect. 1.1 and subsequent ones or even for any model, after some clarification. The analyzed parameters are better estimated by ML/REML if there is no correlation between them. Otherwise, the contours of NLLF can be elongated (Man 2011; Jarmołowski 2016; Segall et al. 2000) and we can expect some problems, possibly also in FSLM. Some cases can even require the use of ratio of the parameters (Pardo-Igúzquiza 1997).

Terrestrial gravity anomalies have a relatively large signal variance at higher frequencies, i.e., the small-scale mass differences can still induce mGals of signal in relation to more global variations. Therefore, limited spatial resolution contributes significantly to the noise covariance matrix, causing signal aliasing in the modeling process and an explicit noise. This property of gravity data is suitable for the estimation of noise variance in the current work. The proposed method of noise variance estimation is representative for these geophysical quantities, which are characterized by significant signal at higher frequencies or are affected by large measurement noise. The first case includes the phenomena, where the sources of significant part of the signal vary at the higher resolutions. Both cases, i.e., large signal lost due to the resolution limit or large survey error, are especially worth analyzing by FSLM.

Terrestrial gravity data provide a good testing sample due to the extensive data base and the existence of accurate global gravity models used here as the long-wavelength part of the signal. The subtraction of the global model contribution, which replaces the deterministic part of the signal (Eq. 1), creates residuals that represent relatively well the stationary nature of the stochastic process. This property is especially useful in practice, bearing in mind the general conditions of LSC (Moritz 1980, p. 76). However, there are specific phenomena in geophysics, where the expected value has no global reference and can be modeled in some approximate way, e.g., using a deterministic model. On the other hand, the deterministic approximation of the expected value can be sometimes sufficient and effective from practical point of view. Summarizing, the proposed FSLM parameter estimation is dedicated for the modeling of residual quantities, having their large-scale representation accurate at the required level.

It can be concluded from the above that FSLM parametrization of the covariance model is applicable to any geophysical quantity and can be used for an arbitrary number of parameters in space and time units. The application to more than two parameters needs to take into account the possible correlation of the parameters in the covariance matrix and data statistical distribution, which is also related to the reference model for detrending.

2 Fisher Scoring of Planar Covariance Model Parameters

LSC is the parametric technique of data modeling based on the covariance matrices of signal and noise. In the current study, signal covariance matrix represents the signal residuals, remaining after the removal of some lower-frequency signal. This rule is called “remove-restore” and is necessary in local LSC modeling, in order to constrain zero expected value for the used data. Therefore, the data are in fact split into three parts: a deterministic signal, residual signal and the noise. A typical mathematical model that is often used in the representation of gravity observations and other physical phenomena in spatial domain is:

$$\varvec{\Delta g} = \varvec{X\beta } + \varvec{s} + \varvec{n}$$
(1)

where Δ g is a vector of gravity anomalies or another correlated data, Xβ is the deterministic part of the signal, s are the signal residuals and n denotes noise. The deterministic part is often represented by multiple regression, where β includes the vector of trend parameters and X is a design matrix of the trend. However, it can be also derived from the global models of the phenomena, e.g., in the form of spherical harmonic expansion. The residual signal covariance can be approximated by the application of Gauss–Markov third-order model (GM3) that reads:

$$C_{s} \left( {C_{0} ,CL,s} \right) = GM3\left( {C_{0} ,CL,s} \right) = C_{0} \left( {1 + \frac{s}{CL} + \frac{{s^{2} }}{3CL}} \right) \cdot \text{exp}\left( { - \frac{s}{CL}} \right)$$
(2)

where s is the distance between two data points and CL is correlation length. This planar covariance model (Moritz 1980, p. 169) is one of the most frequently applied in gravity anomaly modeling (Grebenitcharsky et al. 2005; Moreaux 2008). The covariance matrix C s of the signal is then created using signal variance (C 0) along the diagonal (s = 0) and calculated covariance values for the respective pairs of points. The noise is assumed to be homogeneous, as it is frequent among the applications (Hosse et al. 2014; Sadiq et al. 2010), and the noise covariance matrix is diagonal, i.e.:

$$\varvec{C}_{\varvec{n}} = \delta n^{2} \cdot \varvec{I}_{n}$$
(3)

The total covariance matrix C(θ) = C s  + C n . The NLLF derived from the multivariate normal distribution density model can be described as:

$$\text{NLLF}\left( {\varvec{\Delta g}^{\varvec{r}} ,\varvec{\theta}} \right) = \frac{1}{2}\text{ln}\left| {\varvec{C}\left(\varvec{\theta}\right)} \right| + \frac{1}{2}\text{ln}\left| {\varvec{X}^{\varvec{T}} \varvec{C}\left(\varvec{\theta}\right)^{ - 1} \varvec{X}} \right| + \frac{1}{2}\left( {\left( {\varvec{\Delta g}^{\varvec{r}} } \right)^{T} \varvec{R}\left(\varvec{\theta}\right)\varvec{\Delta g}^{\varvec{r}} } \right)$$
(4)

where C(θ) is the covariance matrix based on the parameters vector θ and Δ g r = Δ g − Xβ is the vector of data residuals. R is Rao’s matrix that reads:

$$\varvec{R}\left(\varvec{\theta}\right) = \varvec{C}\left(\varvec{\theta}\right)^{ - 1} \cdot \left\{ {\varvec{I}_{n} - \varvec{X}\left[ {\varvec{X}^{T} \varvec{C}\left(\varvec{\theta}\right)^{ - 1} \varvec{X}} \right]^{ - 1} \varvec{X}^{T} \varvec{C}\left(\varvec{\theta}\right)^{ - 1} } \right\}$$
(5)

where an additional, planar detrending is applied to Δ g r in order to comply REML rule, i.e.:

$$\varvec{X} = \left[ {\begin{array}{*{20}c} 1 & {\varphi_{1} } & {\lambda_{1} } \\ \cdots & \cdots & \cdots \\ 1 & {\varphi_{n} } & {\lambda_{n} } \\ \end{array} } \right]$$
(6)

The minima of NLLF are the basis for the θ components estimation. These minima can be also determined using FS process (Grodecki 1999; van Loon 2008). The vector of the parameters θ has to be iterated by following the algorithm:

$$\varvec{\theta}_{k + 1} =\varvec{\theta}_{k} - \varvec{S}\left( {\varvec{\theta}_{\varvec{k}} } \right)^{ - 1} \,\cdot\, \varvec{d}_{k} \left( {\varvec{\theta}_{k} } \right), \quad k \in \left\{ {1,2 \ldots z} \right\}$$
(7)

where S(θ) is the Fisher IM produced using first derivatives of the covariance matrix C(θ) and z is the maximum number of iterations. The matrix S(θ) reads:

$$\varvec{S}\left(\varvec{\theta}\right) = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {S_{1,1} } & {S_{1,2} } \\ {S_{i,1} } & {S_{2,2} } \\ \end{array} } & {\begin{array}{*{20}c} \ldots & {S_{1,jmax} } \\ \ldots & {S_{2,jmax} } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots & \vdots \\ {S_{imax,1} } & {S_{imax,2} } \\ \end{array} } & {\begin{array}{*{20}c} \ddots & {S_{i,jmax} } \\ {S_{imax,j} } & {S_{imax,jmax} } \\ \end{array} } \\ \end{array} } \right]$$
(8)

where a component of S(θ) is calculated as:

$$S_{ij} = tr\left( {\varvec{RC}_{i} \varvec{RC}_{j} } \right)\quad i,j = \theta_{i}$$
(9)

The derivatives C i and C j of the covariance matrix must be computed with respect to the covariance parameters from θ, i.e.:

$$\varvec{C}_{i} = \frac{{\partial \varvec{C}\left(\varvec{\theta}\right)}}{{\partial\varvec{\theta}_{\varvec{i}} }}$$
(10)

The vector of scores is d(θ k ) = t(θ k ) – u(θ k ) and

$$\varvec{u} = \left\{ {u_{i} } \right\}$$
(11)

in which the element for respective i must be calculated as:

$$u_{i} = \varvec{\Delta g}^{{\varvec{rT}}} \varvec{RC}_{\varvec{i}} \varvec{R\Delta g}^{\varvec{r}}$$
(12)

The part of NLLF derivative denoted t is composed of

$$\varvec{t} = \left\{ {t_{i} } \right\}$$
(13)

with respective elements derived as

$$t_{i} = tr\left( {\varvec{RC}_{\varvec{i}} } \right)$$
(14)

The derivatives of single element of C(θ) based on Eqs. (2) and (3) that correspond to points p and r are as follows:

$$\frac{{\partial C_{p.r} \left(\varvec{\theta}\right)}}{{\partial C_{0} }} = \text{exp}\left( {\frac{{ - s_{p,r} }}{CL}} \right) \cdot \left( {1 + \frac{{s_{p,r} }}{CL} + \frac{{s_{p,r}^{2} }}{{3CL^{2} }}} \right)$$
(15)
$$\frac{{\partial C_{p.r} \left(\varvec{\theta}\right)}}{\partial \delta n} = 2\delta n$$
(16)
$$\frac{{\partial C_{p.r} \left(\varvec{\theta}\right)}}{\partial CL} = C_{0} \cdot \text{exp}\left( {\frac{{ - s_{p,r} }}{CL}} \right) \cdot \left( {\frac{{s_{p,r} }}{{CL^{2} }}\left( {1 + \frac{{s_{p,r} }}{CL} + \frac{{s_{p,r}^{2} }}{{3CL^{2} }}} \right) - \frac{{s_{p,r} }}{{CL^{2} }} - \frac{{2s_{p,r}^{2} }}{{3CL^{3} }}} \right)$$
(17)

3 Levenberg–Marquardt Optimization of Fisher Scoring

The applications of the FS method have shown inefficiency of its simple form described in Eq. (7). The estimates were often divergent from the global or even from the local minimum of the NLLF. The divergence of the scoring is the most frequently reported problem in the literature (Green 1984; Halimi et al. 2015; Kubik 1970; Sari and Çelebi 2004). Currently, a very promising technique that can overcome this disadvantage is LM optimization. LM algorithm was developed to solve the problem of minimizing a nonlinear function, which also appears also in REML estimation. The FS is a nonlinear least-squares problem, which induces nonlinear iteration and gives no guarantee of the convergence (Smyth 2002a). This problem can be controlled by the use of LM damping. Some authors have already pointed its good convergence in the cases of complex parameters variation (Lourakis and Antonis 2005; More 1977; Yu and Wilamowski 2011). The LM optimization is quite often applied in the estimation by Gauss–Newton or Newton–Raphson methods (Giordan et al. 2014; Harville 1977; Shan 2008) where a Hessian of the covariance matrix has to be inverted. The IM in FS has to be positive definite (Smyth 2002b). On the other hand, the problem pertains to the singularity of the inverted matrix, which often appears in practice, making the convergence impossible (Fan and Pan 2009; Ling et al. 2014; Yang 2013). This paper presents the application of FSLM applied to LSC, which is the most popular technique of gravity field modeling. The vector of the covariance parameters for the planar signal covariance model, after assuming non-correlated noise and approximation of the signal variance C 0, by the use of, e.g., data variance is:

$$\varvec{\theta}= \left[ {\delta n; CL} \right]$$
(18)

This vector is variable in the calculation of covariance matrix C(θ), as well as in the creation of the IM, i.e., S(θ). The goal of the optimization is to assure invertibility of S(θ). The optimized equation of FSLM reads

$$\varvec{\theta}_{k + 1} =\varvec{\theta}_{k} - \left( {\varvec{S}\left( {\varvec{\theta}_{\varvec{k}} } \right) + \mu \cdot \varvec{I}_{{\varvec{imax}}} } \right)^{ - 1} \cdot \varvec{d}_{k} \left( {\varvec{\theta}_{k} } \right),\quad k \in \left\{ {1,2 \ldots z} \right\}$$
(19)

where μ denotes the LM parameter. Shan (2008) and Giordan et al. (2014) are close to the actual study, as they consider resizing of μ parameter, depending on the iteration step. Their classical approach uses larger steps at the beginning, which are hazardous in the further steps and need to be decreased. The current work also takes into account this problem. This study is focused on the relation between the selection of μ parameter and FSLM iteration path. This selection has key influence on FSLM solvability and is also significantly related to the iterations stopping time. The goal of this paper is to apply LM without supporting conditions, which are frequent among the examples in Sect. 1.4. The studies cited in Sect. 1.4 refer to more composed tools controlling FS convergence, which need significantly more computational effort than LM damping.

4 Example Gravity Data for Numerical Study

Nowadays, many physical quantities require a precise interpolation in 2D in order to create spatially regular models, which in some cases are also variable in time. LSC and kriging are still among the leading techniques in modeling of different geophysical data. This study applies gravity anomaly data, which have some helpful testing properties listed in Sect. 1.5, and therefore can be considered as a representative one. Additionally, terrestrial gravity has dense and regular spatial coverage, which makes it handy in the tests. Finally, Bouguer gravity anomalies are free from the height correlation to the suitable level. Terrestrial, Bouguer gravity anomalies have been extracted from the US gravity database, which is available at the Web site of University of Texas at El Paso (Hildenbrand et al. 2002). The original data spacing is variable over the region, but reaches around 0.03° in better covered areas. The spacing 0.03° was used in the analysis shown in Jarmołowski (2016); however, some regions have more sparse data and lower resolution has been applied to keep homogeneity over the entire region in the current analysis. The data are selected to have approximately 0.1° spacing in latitude and longitude. This selection provides a significant and perceivable noise and homogeneous horizontal distribution, convenient in the analysis. The data resolution has a key influence on the noise level (Jarmołowski 2016), which is somewhere between 1 and 3 mGal here.

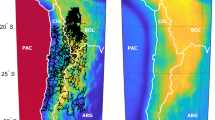
The data are divided into 12 sectors, using 2° intervals in latitude and longitude. The use of 12 sectors is self-explanatory, as it provides a larger sample for the algorithm testing. Around 320 points are included in each sector, which determines the sizes of vectors and matrices in the tested FSLM. Every sector is characterized by different data variance, noise variance and its own data distribution. The numeration of the sectors and data is shown in Fig. 1. Different characteristics of the datasets enable a better test of reliability, but one should be aware that this method can be further applied in different, even extreme data conditions and other factors should be revised. To summarize, the properties of the selected data sample can limit the number of hidden factors adversely affecting the analysis.

Fig. 1
figure 1

Gravity data division and map of gravity residuals

Full size image

The data have been detrended using EGM2008 global geopotential model. The surfaces of Bouguer gravity up to degree and order 360 have been subtracted, which corresponds to the grid step four times denser than each sector size. Most of the long-wavelength signal is therefore removed, preserving a substantial signal part with the variance several times larger than the noise variance.

5 Fisher Scoring with Levenberg–Marquardt Applied to Two Covariance Parameters—Numerical Study

The numerical study describes the detailed investigation of the influence of LM optimization on the results and convergence level of FSLM. It was explained in Sect. 1.4 that the selection of FS, as more promising than NR from the onset, is based on the experiences from numerous examples in the literature and confirmed by preliminary test comparing FS and NR methods. Namely, the performance of NR optimized by LM has been compared to FSLM within 80 iterations, using 12 test data sectors. The steps of NR are more rapid and less accurate in the sense of poor convergence, for similar μ parameters. Increasing μ to really large values (around 40) gives better convergence and smoothness of the track, but needs significantly more iterations and time than FSLM (for μ = 40 the NR has no convergence at 80 iterations). More successful and faster convergence of FSLM confirms previous works comparing FS and NR and makes FSLM a method of choice for the parametrization of LSC.

There are three trials in this numerical study performed with the use of the same covariance model, parameters and under the same assumptions. The only difference between the trials is a range of variable μ, used in order to show its specific properties. The vector θ including CL and δn is iterated in all FSLM trials, whereas C(θ) is based on the sum of signal and noise covariance matrices. The signal covariance matrix is produced from Eq. (2) with C 0 fixed as the signal variance. The noise covariance matrix is calculated from Eq. (2). FSLM is applied in the parametrization of GM3 model (Eq. 2) with μ = 0 and with variable levels of LM optimization to reveal the practical effect of μ selection on the convergence way, by observing regularity and speed of the convergence, as well as the direction and size of the iteration steps. The number of the iterations z is primarily set to 70; however, the iteration results with smaller μ stop varying after less than 20 (Table 1). The order of magnitude for the parameters units seems to be a very important issue here, since the estimation of CL in degrees has shown serious numerical problems. The use of kilometers solves the problem when δn is in mGals, but it is possible that some normalization has to be applied in the case of numerically inconsistent units of the parameters. A further analysis has shown that a numerical relation between the sizes of analyzed parameters may even constitute a crucial issue there. The controlling of the parameters changes ratio contributes significantly to the stability of the solution.

Table 1 The results of FSLM with μ = 1
Full size table

The first trial uses three empirically selected values of μ (0, 1 and 10) to observe the convergence path and its smoothing with the increase in μ. Initially, FS has been used with no LM optimization (μ = 0), as the option with no LM optimization often occurs in the geodetic literature (Grodecki 2001; van Loon 2008). The weak results of this inadequate FS approach to the case of spatial data signal and noise parameters search are shown in Fig. 2. Figures 2, 3 and 4 describe the successive iterations of FS marked with the red line and smaller red dots with the last (70th) iteration denoted by the large red dot. The background of these figures is the contours of REML values calculated from the NLLF using ranges: CL = {1, 0.5–40} and δn = {0.01, 0.2–40.01}, with the minimum NLLF value denoted by white, large dot (Eq. 4). Sometimes, the white dot is not visible, which means that the result of the iterations completely diverges from the minimum. Successful iterations in Fig. 2 refer to 6 out of 12 sectors of the gravity residuals. The condition of the success is based on the difference between the individual parameter iteration result and the covariance parameter estimated from the minimum of NLLF calculated from Eq. (4). The threshold for this success is set to 0.5 for CL and to 0.3 for δn. The threshold values are based on the available resolution of NLLF contours values and the approximation of accuracy lower bounds obtained from IM, which will be discussed later. It was proven in Jarmołowski (2013, 2016) that this precision of CL and δn is enough for the accurate LSC and therefore such threshold of success resolves both the independent control of the correctness and the accuracy issue.

Fig. 2
figure 2

The results of FS with μ = 0 over the contours of NLLF values. The iterations fail in many sectors due to unstable scoring algorithm. The instability is also visible in the remaining ones

Full size image
Fig. 3
figure 3

The approach of FSLM to NLLF minimum with μ = 1 over the contours of NLLF values. The iterations are successful in all sectors with sufficient accuracy. However, the search path shows residual instability

Full size image
Fig. 4
figure 4

The approach of FSLM to NLLF minimum with μ = 10 over the contours of NLLF values. The iterations are successful in all sectors and equal to those from Fig. 3. The search path has smooth shape and converges consequently

Full size image

The scaling of the axes in Fig. 2 is intentionally various, and even not similar in one subfigure in case of FS failure. Axes shown in Fig. 2 are dependent on the FS results to show the range of divergence from the minimum. The tracks converge very irregularly in the case of success in Fig. 2. The absence of the last iteration mark in Fig. 2c indicates insolvability leading to the value out of the numerical variable range in MATLAB. The ranges of the axes in some other cases also denote serious numerical problems when μ = 0.

The first trial also includes recalculations of FS optimized by LM with μ = 1 and μ = 10 (Figs. 3, 4), which are also compared to NLLF values and shown as zoomed in, except Fig. 3a and 4a. These two subfigures depict smooth start of iterations with μ = 1 (Fig. 3a) and μ = 10 (Fig. 4a). The remaining subfigures present the further iterations up to 70th. The zoomed in subplots in Figs. 3 and 4 reveal parts of the search tracks, which are not-observable in Fig. 2. It should be pointed out that their resolution can be insufficient to depict the latest iteration steps, especially in Fig. 3, as they are prepared to show the approach of search track to REML minimum. FSLM with μ = 1 provides successful scoring estimates in all sectors of data after 8–14 iterations, which takes around 1–2 s for each sector, using typical i5 processor (Table 1). The assumed 70 iterations are done after around 10 s. The track of the iteration converges to the global NLLF minimum quite quickly and starts more regularly than in Fig. 2 (Figure 3a). However, in the close neighborhood of NLLF minima the tracks have some remaining irregularity in the direction of search, which will be discussed in the following paragraphs (Fig. 3b–l). Figure 4 illustrates the application of μ = 10 and presents a smooth path of the iterations, as well at the start of the algorithm (Fig. 4a), as for the iterations that approach to the true NLLF minimum (Fig. 4b–l).

The inverse of IM can be used to approximate the accuracy of the estimated parameters (Han and Xu 2008; Kitanidis 1983; Searle et al. 1992). Square roots of the diagonal elements from IM inverse provide the lower bound of accuracy of CL and δn parameters (Tables 1, 2). These bounds correspond to the resolution of NLLF contours calculation in this analysis and therefore the assumed threshold of FSLM success is justifiable. On the other hand, the accuracy requirements for the covariance parameters in LSC are quite moderate, i.e., a few tenths of km and mGal will provide good LSC results here. Definitely, a more important condition related with the parametrization is to avoid significantly wrong parameters, which often happens in the case of noise variance. The tables also present the results of FSLM for μ = 1 and μ = 10, i.e., CL and δn estimates, number of the iterations and time to success. The estimates of covariance parameters are mostly equal for two optimization parameters, as well as the lower error bounds. The time of the calculation is around 2–4 times larger for μ = 10 than for μ = 1 (Tables 1, 2; Fig. 5).

Table 2 The results of FSLM with μ = 10
Full size table
Fig. 5
figure 5

Number of iterations (a) and approximate time (b) necessary to converge with REML minimum for various μ parameters. For μ = 0, 70 unsuccessful iterations have been made in some sectors, which resulted in a large computing time. For μ from 1 to 10, the success needs increasingly more time and iterations, but these numbers do not grow rapidly

Full size image

A complementary, second trial has been made for μ from 1 to 10 with natural step 1 in order to observe the number of iterations and time of calculation in more details. Figure 5 reveals a wide range of iterations and time depending on the data sector, even for the same μ. On the other hand, the increase in the time and iteration number is moderate with respect to increasing μ. The times of the iterations for μ = 0 in Fig. 5b are results of full 70 iterations (Fig. 5a) in case of unsuccessful FS.

The last (third) trial is focused on the questions related with Figs. 3 and 4 and Tables 1 and 2 and refers to the reliability of the smaller values of μ in FSLM. The success of FSLM with μ = 1 has been attained; however, some uncertainty related with the irregular path (Fig. 3) remains, as well as the concern about the smooth descent in Fig. 4. In order to know more, a detailed analysis of the search path should be performed in practical calculations. The ratio between optimal CL and δn parameters known from NLLF calculation is around 0.1, as CL is close to 10 km and δn is around 1–2 mGal. Figure 6 shows the plot of the absolute value of the ratio between CL and δn changes in the consecutive iterations, for all 12 sectors and various μ. The absolute value of the estimated ratio of parameters changes can be only observed in the plot with a logarithmic scale of the y-axis. The failures with μ = 0 (Fig. 2c, e, g, i–k) are all related with the total change of this ratio up to a very large (or small) number (Fig. 6m). There are also some discontinuities coming from the numerical exceeding of double precision range. Figure 6n presents the same situation for μ = 0.01, where three failures are obtained (more figures of tracks are avoided). Figure 6o–s represents a reasonable relation between the parameters, and all these plots represent successful FSLM. However, the results in Fig. 6o, p differ from these in Fig. 6r, s, i.e., residual variations of the ratio can be observed in two former subfigures. Additionally, Fig. 6o can be compared to Fig. 3 and one can see that variations of CL/δn change ratio are reflected in the unstable FSLM tracks. Otherwise, in Fig. 6r the variations of the ratio disappear and consequently Fig. 4 shows all search tracks smoothly and regularly descending to NLLF minima. The time amount and iterations number are of course larger for the larger μ, but the increase is not enormous, i.e., 2–4 times more for μ = 10 than for μ = 1 (Fig. 5).

Fig. 6
figure 6

The absolute value of parameters ratio changes for the selected μ parameters. This ratio is extremely unstable for μ < 1 and causes FSLM failure. The unstable ratio for μ = 1 or 5 results in irregular search path, e.g., in Fig. 3. The smooth change of ratio for μ = 10 and 15 guarantee a consequence and smoothness of the search (Fig. 4)

Full size image

Knowing now that the ratio gives in fact a tangent of the direction, it becomes interesting what the detailed behavior is of the search direction in its polar coordinates unit. Therefore, a complementary Fig. 7 based on 12 sectors and 6 different μ values has been prepared to describe again some interesting smoothness and stability for the larger μ (Fig. 7p–s). The unstable search path for μ = 1 (Fig. 3) raises a question, if the process is sufficiently smoothed to be safely well-posed in practice? The iterations are successful in Fig. 3; however, the variations of the direction for μ = 1 start fairly before the tenth iteration and reveal possible close risk of failure (Fig. 7o). Of course, additional algorithms based on constraints, conditions, etc., can be applied to help in the convergence (Ahn et al. 2012; Osborne 1992; Wang 2007). However, one should always take into account the speed of combined methods and determine if large steps of FSLM are necessary at any stage.

Fig. 7
figure 7

The changes of search direction for the selected μ parameters. These changes can vary extremely up to μ = 1 or 5. Larger μ provides a stable search direction during all iterations

Full size image

In order to investigate the size of the iteration steps, additional comparison has been made for δn and CL changes separately (Fig. 8). Absolute values of δn and CL changes are presented jointly using solid and dashed lines, as their scales are similar despite different units. Figure 8m, n shows cases of the failures, but in line with previous observations, a better way to avoid the failure is to observe their ratio (Fig. 6). Figure 8m–p presents descending of the parameters changes to 10−16, which is a limit of double precision, so it descends to zero. This decrease can be assessed as the convergence at first look; however, after comparison with Table 1 it is evident that maximum iteration number at success for μ = 1 is 14, whereas all plots in Fig. 8o descend after 20 iterations. Therefore, it is clear that the oscillations around zero arise after practical convergence point and during the approach to NLLF minima; we can observe rather gradual and consistent changes of parameters. Summarizing, the zero size steps always occur in a certain number of iterations after practical convergence and appear as useless for the stopping criteria. However, it can be observed that the start of δn and CL rapid decrease (Fig. 8o, r) takes place approximately around the convergence point, respectively, between iterations 8–14 (Table 1) and 25–61 (Table 2). In Figs. 6r and 7r, the direction also stabilizes within this interval. The only question that remains is how small the parameters differences should be to stop the iteration process.

Fig. 8
figure 8

The changes of step sizes for the selected μ parameters, for individual covariance parameters. The iterations fail in many sectors with μ = 0 or 0.1. The algorithm tries to rapidly reduce the steps with μ = 1, whereas larger μ enables more gentle and stable step reduction

Full size image

6 Conclusions

The most frequently discussed problem referring to the efficiency of FSLM, as well as Newton-like algorithms, is the defective convergence of the iterations. Many researchers try to solve this drawback, often using combined techniques, based on various statistical and geometrical conditions. This case study aims at providing some additional numerical results obtained with a considerable data set, which depict the detailed influence of μ parameter selection on the iteration path. These results can be useful for simplifying the controlling of the FSLM process and may encourage taking FSLM into account, as a fast and straightforward technique.

The non-optimized FS fails in many cases and it is clear that it cannot be used in the applications. The assumed GM3 model has been successfully parametrized for all 12 data samples, starting from μ = 1 or even slightly smaller. The first FS efficient in 12 sectors in Fig. 5, which is fastest at the same time, occurs for μ = 1. However, in the corresponding Fig. 6o the ratio of the parameters changes oscillates significantly, as the plot with a logarithmic scale of the y-axis. These oscillations cause a significant change of the directions (Fig. 7o), which is also reflected in many sectors in Fig. 3, as an irregular search path. In contrast, ΔCL/Δδn ratio in Fig. 6r and search direction in Fig. 7r have smooth plots or stop change after some iterations, which gives smooth search tracks in Fig. 4. These findings shows us that the range of useful μ parameter may be quite wide; however, different μ provide different level of the iteration track regularity. The lower μ values are still dangerous due to the failure risk, whereas the upper take more time and iterations. Therefore, a useful test before the selection of the robust μ should incorporate the investigation of track direction stability over a large number of iterations. Additionally, we may need to assist ourselves with Fig. 5, to determine our requirements in respect to time that we accept and to decide if we need safe and robust estimation from any starting values or if we want setting the conditions in the code and more control of the iterations. Another question is how much time must be spent on additional iterations in relation to the conditions. In the case of LSC parametrization, the time of safe FSLM with μ = 10 is still reasonable and therefore the smooth, more robust solution can be very interesting in the further tests. It should be also mentioned that the iteration time is relative here, as stronger processors and languages can be used, even now.

The extremely large ratio of CL/δn differences in Fig. 6m, n indicates absolute failures in all these cases (plots of tracks failures for μ = 0.01 are omitted). This is an important observation in this study, and this can be a powerful condition to keep the iterations far from the failure. It was mentioned that the units of the parameters and their true ratio were intentionally set to be close to unity (0.1–0.2), because the initial tests with larger true ratio have provided significantly more failures.

The comparison in Fig. 8 provides a partial answer to the stopping criterion for the iteration number. The changes of the parameters start to descend more rapidly around the convergence point; however, the exact zero is several iterations after attaining NLLF minimum with assumed accuracy. It is possible that a gradient of their fall will be helpful in the determination of the stopping place.

FSLM applied in the parametrization of LSC is much faster than REML calculated via NLLF, much faster than any CV technique and significantly faster than ECF calculation and least-squares or manual fit of the analytical model, even for larger μ. Additionally, the FSLM can be an automatic procedure, whereas the fitting of the model into ECF is known for an unavoidable manual control of the process. The results show that ECF can be efficiently substituted by FSLM in the parametric methods of spatial data modeling like LSC or kriging. The idea of LM optimization looks promising for FS, even in automated practice. The future applications of FSLM can be extended to, e.g., estimation of heterogeneous noise variances or other variance components. However, the observations provided in the article also need some more testing to complete the method of μ selection.