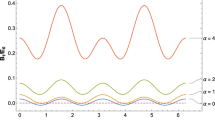
Abstract
We present strategies how to reconstruct (estimate) properties of a quantum channel described by the map E based on incomplete measurements. In a particular case of a qubit channel a complete reconstruction of the map E can be performed via complete tomography of four output states E[ρj] that originate from a set of four linearly independent “test” states ρj (j = 1,2,3,4) at the input of the channel. We study the situation when less than four linearly independent states are transmitted via the channel and measured at the output. We present strategies how to reconstruct the channel when just one, two or three states are transmitted via the channel. In particular, we show that if just one state is transmitted via the channel then the best reconstruction can be achieved when this state is a total mixture described by the density operator ρ = I/2. To improve the reconstruction procedure one has to send via the channel more states. The best strategy is to complement the total mixture with pure states that are mutually orthogonal in the sense of the Bloch-sphere representation. We show that unitary transformations (channels) can be uniquely reconstructed (determined) based on the information of how three properly chosen input states are transformed under the action of the channel.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Jaynes E.T. (1963). “Information theory and statistical mechanics,” in 1962 Brandeis Lectures Benjamin, Elmsord New York
Poyatos J.F., Cirac J.I., Zoller P. (1997). “Complete characterization of a quantum process: The two-qubit quantum gate”. Phys. Rev. Lett. 78, 390
D’Ariano G.M., Lo Presti P. (2001). “Quantum tomography for measuring experimentally the matrix elements of an arbitrary quantum operation”. Phys. Rev. Lett. 86: 4195
G.M. D’Ariano and P. Lo Presti, “Characterization of quantum devices,” in Quantum Estimations: Theory and Experiment—Springer Series on Lecture Notes in Physics (Springer-Verlag, Berlin, 2004).
Peres A. (1995). Quantum Theory: Concepts and Methods. Kluwer Academic, Dordrecht
Nielsen M., Chuang I. (2000). Quantum Computation and Quantum Information. Cambridge University Press, Cambridge
Ježek M., Fiurášek J., Hradil Z. (2003). “Quantum inference of states and processes”. Phys. Rev. A 68, 012305
M. Raginski, “Quantum system identification,” Proceedings of the International Conference “Physics and Control” (PhysCon 2003) (A. L. Fradkov and A. N. Churilov, eds.), St. Petersburg, Russia, 2003 Vol. 3: Control of Microworld Processes. Nano- and Femtotechnologies, pp. 792–796 [see also quant-ph/0306008 (2003)].
Ruskai M.B., Szarek S., Werner E. (2002). “An analysis of completely positive tracepreserving maps on 2× 2 matrices”. Lin. Alg. Appl. 347, 159
King C., Ruskai M.B. (2001). “Minimal entropy of states emerging from noisy quantum channels”. IEEE Trans. on Inf. Theory 47, 192
Choi M.D. (1975). “Completely positive linear maps on complex matrices”. Lin. Alg. Appl. 10, 285
Fujiwara A., Algoet P. (1999). “One-to-one parametrization of quantum channels”. Phys. Rev. A 59: 3290
Alberti P.M., Uhlmann A. (1980). Rep. Math. Phys. 18, 163
Author information
Authors and Affiliations
Additional information
We have originally dedicated this paper to Asher Peres on the occasion of his 70th birthday. Unfortunately, since the submission of the paper for publication Asher Peres passed away so we dedicate this paper to his memory.
Rights and permissions
About this article
Cite this article
Ziman, M., Plesch, M. & zek, V.B. Reconstruction of Superoperators from Incomplete Measurements. Found Phys 36, 127–156 (2006). https://doi.org/10.1007/s10701-005-9009-9
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10701-005-9009-9