Pollutant Dispersion in Boundary Layers Exposed to Rural-to-Urban Transitions: Varying the Spanwise Length Scale of the Roughness

Abstract

Both large-eddy simulations (LES) and water-tunnel experiments, using simultaneous stereoscopic particle image velocimetry and laser-induced fluorescence, have been used to investigate pollutant dispersion mechanisms in regions where the surface changes from rural to urban roughness. The urban roughness was characterized by an array of rectangular obstacles in an in-line arrangement. The streamwise length scale of the roughness was kept constant, while the spanwise length scale was varied by varying the obstacle aspect ratio l / h between 1 and 8, where l is the spanwise dimension of the obstacles and h is the height of the obstacles. Additionally, the case of two-dimensional roughness (riblets) was considered in LES. A smooth-wall turbulent boundary layer of depth 10h was used as the approaching flow, and a line source of passive tracer was placed 2h upstream of the urban canopy. The experimental and numerical results show good agreement, while minor discrepancies are readily explained. It is found that for $l/h=2$ the drag induced by the urban canopy is largest of all considered cases, and is caused by a large-scale secondary flow. In addition, due to the roughness transition the vertical advective pollutant flux is the main ventilation mechanism in the first three streets. Furthermore, by means of linear stochastic estimation the mean flow structure is identified that is responsible for street-canyon ventilation for the sixth street and onwards. Moreover, it is shown that the vertical length scale of this structure increases with increasing aspect ratio of the obstacles in the canopy, while the streamwise length scale does not show a similar trend.

1 Introduction

Because there is a worldwide increase in urbanization, more pollutant emission sources, such as from power generation, households and traffic, are present near populated areas. As a consequence, the demand for accurate urban air quality predictions is rising, which requires proper understanding of the dispersion of pollutants in the urban environment. Investigations of the urban boundary layer are often made for fully-developed flow over areas with uniform properties. For example, Cheng and Castro (2002b) carried out experiments on turbulent boundary layers where the complete bottom wall of the wind tunnel was covered with cubical roughness elements, thereby representing the flow over an urban area. In multiple simulation studies the fully-developed character of the flow is implicitly assumed by employing periodic boundary conditions in the horizontal directions (e.g., Coceal et al. 2006; Michioka et al. 2014; Boppana et al. 2014). However, in reality the surface roughness changes, e.g. from rural to urban regions, and the boundary layer has to adapt to this roughness transition. There are only a few recent numerical studies on turbulent flow over an explicitly resolved roughness transition (Lee et al. 2011; Cheng and Porté-Agel 2015), where mostly cubical roughness elements or riblets are considered. In addition, experimental investigations with results up to the roughness elements are scarce, and if a roughness transition is considered it is to determine when the boundary layer retains an equilibrium state, without investigating pollutant dispersion (Cheng and Castro 2002a).

In order to obtain insight in pollutant dispersion mechanisms, Michioka et al. (2014) performed large-eddy simulations (LES) on fully-developed flow over an array of obstacles with various aspect ratios l / h, where l is the spanwise obstacle length and h is the obstacle height. They conclude that for fully-developed conditions the turbulent pollutant flux is the main contributor to street-canyon ventilation, although the ratio of the turbulent to the advective pollutant flux does change slightly for different aspect ratios. Tomas et al. (2016) show that up to 14h downstream of a rural-to-urban roughness transition the advective pollutant flux remains significant. Furthermore, Michioka et al. (2011, 2014) conclude that street-canyon ventilation mostly takes place when low momentum regions pass over the canyon, and they suggest that these regions are of small scale compared to the coherent structures in the outer region and are generated close to the top of the canopy.

Currently, there are few experimental investigations on urban geometries in which concentration fields and velocity fields are measured simultaneously, such that dispersion mechanisms can be investigated (Vinçont et al. 2000). To the authors’ knowledge there is no such experimental data available for regions containing multiple street canyons that allow a study on the streamwise development. Therefore, we use both LES and experimental measurements to investigate pollutant dispersion mechanisms for a rural-to-urban roughness transition, and in neutrally buoyant conditions. The set-up is similar to Tomas et al. (2016), where the urban canopy consists of cubical obstacles in an in-line arrangement. In addition, various urban canopies are considered by varying the spanwise aspect ratio of the obstacles. The experiments were carried out in the water tunnel at the Laboratory for Aero- and Hydrodynamics at the Delft University of Technology using simultaneous stereoscopic particle image velocimetry (PIV) and laser-induced fluorescence (LIF) techniques in order to investigate instantaneous pollutant dispersion mechanisms. The objectives are, (1) to set up a well-validated dataset for flow and pollutant dispersion and (2) to answer the following questions:

• What is the influence of the aspect ratio l / h on flow over a rural-to-urban transition, in terms of velocity statistics, internal boundary-layer depth, surface forces, and pollutant dispersion?

• What are the dominant mechanisms of pollutant removal from street canyons and how do these mechanisms change in the transition region?

In Sect. 2 the details of the considered cases are given, as well as information on the experimental set-up, measurement techniques, and the numerical method. Section 3 covers the comparison of the experimental and numerical turbulent inflow profiles, the presentation of the flow statistics, as well as the surface forces and internal boundary-layer growth. In Sect. 4 the experimental and numerical results on pollutant dispersion are presented, and the pollutant dispersion mechanisms are investigated. Finally, in Sect. 5 the conclusions are given.

Fig. 1

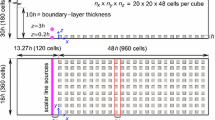
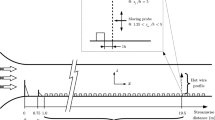
A schematic overview of the experimental and numerical set-up (a) and an overview of the cases that are considered in the experiments and in the simulations (b). The experimental set-up is shown by black lines and dark grey obstacles, while the numerical domain is shown by blue lines and light grey obstacles. The green line represents the laser sheet

2 Materials and Methods

2.1 Considered Cases

In both the experiments and the simulations a smooth-wall turbulent boundary layer was generated that approached an urban roughness geometry consisting of an array of obstacles. The Reynolds number of the approaching flow, $Re_\tau = u_\tau \delta _{99} / \nu$, based on the fluid kinematic viscosity $\nu$, the friction velocity $u_\tau =\sqrt{\nu \partial u /\partial z}$, and the boundary-layer depth $\delta _{99}$, was $2.0\times 10^3$ in both cases. Figure 1a shows the top view and the side view of both the experimental set-up (black lines) and the domain used in the LES (blue lines). The location $x=0$ corresponds to the upstream walls of the first row of obstacles, while the plane $y=0$ lies in the middle of the domain at the symmetry plane of the obstacles. A uniform street layout of obstacles placed in an in-line arrangement was considered to capture the basic characteristics of urban areas. The parameter that was varied is the obstacle aspect ratio l / h; aspect ratios of 1, 2, 3.5, 5, 8, and $\infty$ were simulated by LES, while aspect ratios of 1, 5, and 8 were investigated in the experiments. Figure 1b shows the top view of the different cases, which are indicated by AR1, AR2, AR3.5, AR5, AR8, and 2D. For each case two ‘streets’ are shown that consist of an obstacle row and a ‘street canyon’, which indicates a canyon in spanwise direction unless stated otherwise. In all cases the width of the obstacles as well as the width of all street canyons was equal to h. Consequently, the plan area density $\lambda _\text {p} = A_\text {p}/A_\text {t}$ was equal to the frontal area density $\lambda _\text {f} = A_\text {f}/A_\text {t}$, where $A_\text {t}$ is the total area viewed from the top, $A_\text {p}$ is the total area covered with obstacles and $A_\text {f}$ is the total frontal area of the obstacles. $\lambda =\lambda _\text {f}=\lambda _\text {p}$ was between 0.25 (case AR1) and 0.5 (case 2D), and all cases were in the skimming flow regime (Oke 1988). In addition, a line source of passive tracer was placed in front of the urban environment to simulate an emission from a highway as is often found near urban regions. Its location was 2h upstream of the first row of obstacles. In the experiments the tracer was released from the ground surface, while in the simulations the source was located at $z/h=0.2$. After these properties of the test cases were determined, the experiments and simulations were done independently.

2.2 Experimental Set-Up

2.2.1 Layout

The transparent test section of the water tunnel has a length of 5.0 m and a cross section of $0.6\times 0.6$ $m ^2$, which enables good access for optical measurement techniques, as in the currently employed PIV and LIF techniques.

A false bottom, with dimensions $4.5\times 0.6$ $m ^2$, was mounted 0.17 m above the bottom tunnel wall to limit the influence of remaining flow disturbances emanating from the contraction to the measurement section, as well as to allow the placement of the scalar line source. As shown by Irwin (1981), an artificially thickened boundary layer can be obtained by employing so-called spires. In the current experiment four of these Irwin-type spires were mounted 0.50 m downstream of the sharp leading edge, and spanwise homogeneity of the flow was optimized by their placement. A schematic drawing indicating the different components of the experimental set-up is given in Fig. 2. An additional fence with a height of 0.02 m was placed 0.12 m upstream of the spires in order to generate an additional momentum deficit at the start of the boundary-layer development, as in, for instance, Savory et al. (2013). As flat terrain is considered as the upstream fetch, no additional roughness elements were added downstream of the spires. The resulting boundary layer was first characterized without the urban model by means of a planar PIV measurement in the $y=0$ plane, which is the symmetry plane in the middle of the plate.

Fig. 2

Schematic overview of the experimental set-up indicating the different components

The urban model was placed approximately 3.9 m downstream of the spires. It was constructed from blocks made of Plexiglass with cross-sectional dimensions of $0.02\times 0.02$ $m ^2$ and lengths of 0.02, 0.10, and 0.16 m for cases AR1, AR5, and AR8, respectively. The model contained eight street canyons in streamwise direction. Based on initial results from LES (Tomas et al. 2016), this was deemed to be sufficient to capture the flow development up to the region where the flow in the street canyons becomes similar.

To perform simultaneous velocity and concentration measurements above and partly inside the canopy, a stereoscopic PIV set-up was combined with a planar LIF set-up, as shown in Fig. 2. For the stereoscopic PIV measurements, the flow was seeded with 10 $\mu$m diameter neutrally buoyant tracer particles (Sphericell). The $y=0$ plane was illuminated with a twin-cavity double pulsed Nd:YAG laser (Spectra-Physics Quanta Ray), resulting in a field-of-view of approximately $0.43\times 0.25$ $m ^2$ ($x\times z$). Dedicated optics were used to form a thin laser sheet with a thickness of approximately 1 mm in the measurement area. The particle images were recorded using two high resolution CCD cameras with a $4872\times 3248$ pixel format (Image LX 16M, LaVision). Both PIV cameras were equipped with Micro-Nikkor F105mm objectives with an aperture number of 8. Additionally, both cameras were equipped with Scheimpflug adapters (Prasad and Jensen 1995) to allow for large viewing angles while keeping the particle images in focus. The total separation angle between the PIV cameras was set to $56^{\circ }$. To enable measurements partly inside the canopy, both cameras had a small vertical inclination of about $10^{\circ }$, with a third camera (Image LX 16M, LaVision) added to perform the planar LIF measurements. This camera was also equipped with a Micro-Nikkor F 105mm objective with an aperture number set to 2.8. A lower aperture number was chosen to collect a larger amount of the fluorescent signal. To provide a better view into the canopy this camera had a slight vertical inclination of $10^{\circ }$, thereby eliminating the need for a Scheimpflug adapter. In order to separate the scattered light by the tracer particles (PIV) and the fluorescent signal (LIF), shortpass optical filters (PIV cameras) and a longpass optical filter (LIF camera) were employed (Westerweel et al. 2009).

2.2.2 PIV Measurements

Data acquisition, image calibration, and analysis of the PIV images was performed using the commercial software package Davis 8.3. A custom-made calibration target was used to digitally backproject the distorted PIV images to remove the perspective deformation in stereoscopic viewing. The PIV images were interrogated with a multi-pass interrogation technique, where the final interrogation windows had a size of $24\times 24$ pixels, corresponding to a spatial resolution of 0.1h, with 75% overlap between the neighbouring windows. The fraction of spurious vectors was found to be <2%; these could be reliably detected using a median test (Westerweel and Scarano 2005) and replaced by linear interpolation. Each dataset consisted of at least 1500 instantaneous velocity/concentration fields acquired at a temporal resolution of 1.44 Hz. This low acquisition frequency ensured that subsequent samples could be considered as statistically uncorrelated. As a result, reliable and accurate first-order and second-order statistics could be obtained.

2.2.3 LIF Measurements

As the laser operated at a frequency-doubled wavelength of 532 nm, Rhodamine WT (Rh-WT) was selected as the fluorescent dye, which has spectral characteristics similar to the more commonly used Rhodamine B (Rh-B). However, it is much less toxic (Crimaldi 2008). Although Rh-WT is a temperature sensitive fluorescent tracer (Smart and Laidlaw 1977), the effect of temperature variations was negligible, because the water temperature varied by <1 $^{\circ }$C. The Schmidt number ($Sc = \nu /D$, where D is the mass diffusivity) of Rh-WT in the experiments was approximately $2.5\times 10^3$. Furthermore, the effective resolution of the concentration fields was 0.004h in both directions. The dye was injected 2h upstream of the first row of obstacles as a uniform line source, that consisted of a porous metal plate with size $0.01\times 0.40$ $m ^2$ ($L_x \times L_y$), which was mounted flush with the ground plate. A concentrated solution Rh-WT (10 mg $l ^{-1}$) was injected at a constant flow rate of 3 ml $s ^{-1}$ by means of a syringe pump system, that resulted in an average vertical injection velocity of about $0.75\times 10^{-3}$ m $s ^{-1}$ or $3\times 10^{-3}\,U_\infty$, where $U_\infty$ is the freestream velocity.

After each experiment, a calibration of the LIF images, i.e. the conversion of raw digital images to concentration fields, was done by placing a small Plexiglas container of size $0.45\times 0.12\times 0.04$ $m ^3$ in the measurement domain, with different known uniform concentrations. This yielded a calibration curve for measured pixel grey values to concentrations for each pixel in the measurement domain. Care was taken to perform all experiments under so-called ‘optically thin’ conditions. Accordingly, the attenuation of the laser sheet due to the presence of Rh-WT was negligible, and the conversion of raw images to concentration fields simplified significantly (Crimaldi 2008; Krug et al. 2014). The raw images were converted to a concentration field after subtraction of a background image based on linearly interpolating the background image that was taken before and after each measurement to account for the increase in background levels due to the dye introduced during each measurement. In addition, a rescaling procedure was applied to compensate for the pulse-to-pulse variations (with a standard deviation of about 3% of the mean intensity) that are inherently present in the laser beam of the Nd:YAG laser. Finally, the concentration fluxes are obtained by interpolating the velocity field onto the high resolution LIF grid by bicubic interpolation.

2.3 Numerical Set-Up

The LES set-up is the same as in Tomas et al. (2016) except that in the current study only neutrally buoyant conditions are considered and that several obstacle aspect ratios are studied. Here, the main characteristics of the simulations are given, while further details can be found in Tomas et al. (2016).

2.3.1 Governing Equations and Numerical Method

The filtered continuity equation and the filtered Navier–Stokes equations for incompressible flow are

$$\begin{aligned} \frac{\partial \widetilde{u}_i}{\partial x_i}=&\,0, \end{aligned}$$

(1)

$$\begin{aligned} \frac{\partial \widetilde{u}_i}{\partial t} =&-\frac{\partial }{\partial x_j}\left( \widetilde{u}_i\widetilde{u}_j\right) -\frac{\partial }{\partial x_i}\left( \frac{\widetilde{p}+\tau _{kk}/3}{\rho }\right) + \nu \frac{\partial ^2\widetilde{u}_i}{\partial x_j^2} +\frac{\partial }{\partial x_j}\left( 2\nu _\mathrm{sgs}S_{ij}\right) , \end{aligned}$$

(2)

$$\begin{aligned} \frac{\partial \widetilde{c^*}}{\partial t} =&-\frac{\partial }{\partial x_j}\left( \widetilde{c^*}\widetilde{u}_j\right) + \frac{\nu }{Sc}\frac{\partial ^2\widetilde{c^*}}{\partial x_j^2} +\frac{\partial }{\partial x_j}\left( \frac{\nu _\mathrm{sgs}}{Sc_\mathrm{sgs}}\frac{\partial \widetilde{c^*}}{\partial x_j}\right) + \mathcal {S}, \end{aligned}$$

(3)

where $\widetilde{(..)}$ denotes filtered quantities, $\left( \widetilde{p}+\tau _{kk}/3\right) /\rho$ is the modified pressure, $\tau _{kk}$ is the trace of the subgrid-scale (SGS) stress tensor, $\nu$ is the fluid kinematic viscosity, $\nu _\mathrm{sgs}$ is the SGS viscosity, $Sc_\mathrm{sgs}$ is the SGS Schmidt number, $S_{ij}=\frac{1}{2}\left( \frac{\partial \widetilde{u}_i}{\partial x_j} + \frac{\partial \widetilde{u}_j}{\partial x_i}\right)$ is the rate of strain tensor, and $\mathcal {S}$ is a source term. The eddy-viscosity SGS model, $\tau _{ij}/\rho = \widetilde{u_iu_j} - \widetilde{u}_i\widetilde{u}_j=-2\nu _\mathrm{sgs}S_{ij}$, where $\tau$ is the SGS stress tensor, is already incorporated in Eqs. (2) and (3). Equation (3) describes the transport equation for the pollutant concentration $c^*$. Hereafter the $\widetilde{(..)}$ symbol is omitted for clarity, while the $\overline{(..)}$ symbol represents temporal averaging, and the $\overline{\langle ..\rangle }$ symbol represents spatial averaging.

The code developed is based on the Dutch Atmospheric Large-Eddy Simulation (DALES) code (Heus et al. 2010), where the main modifications are the addition of an immersed boundary method (Pourquie et al. 2009), the implementation of inflow/outflow boundary conditions, and the application of the eddy-viscosity SGS model of Vreman (2004). This model has the advantage over the standard Smagorinsky–Lilly model (Smagorinsky 1963; Lilly 1962) that no wall damping is required to reduce the SGS viscosity near walls. The equations of motion are solved using second-order central differencing for the spatial derivatives and an explicit third-order Runge–Kutta method for time integration. For the scalar concentration field the second-order $\kappa$ scheme is used to ensure monotonicity (Hundsdorfer et al. 1995). The simulations are wall-resolved, so no use is made of wall functions. The Schmidt number Sc was 0.71, and $Sc_\mathrm{sgs}$ was set to 0.9, equal to the turbulent Prandtl number found in the major part of the turbulent boundary layer in direct numerical simulation (DNS) studies by Jonker et al. (2013). The code has been used previously to simulate turbulent flow over a surface-mounted fence, showing good agreement with experimental data (Tomas et al. 2015a, b).

2.3.2 Domain and Boundary Conditions

Figure 1 shows the LES domain in blue together with the applied number of grid cells in each direction. Vertical grid stretching was used such that each (cubical) obstacle was covered with $20\times 20\times 48$ ($x \times y \times z$) cells. At the ground and the obstacle walls no-slip conditions were applied. The velocity and the concentration fields were assumed to be periodic in the spanwise direction. Furthermore, the smooth-wall turbulent boundary layer imposed at the inlet was generated in a separate ‘driver’ simulation using the rescaling method proposed by Lund et al. (1998). At the outlet a convective outflow boundary condition was applied for both velocity and concentration. Furthermore, at the top wall free-slip conditions were assumed for the horizontal velocity components. In addition, a small vertical outflow velocity was applied that corresponds to the outflow velocity used in the driver simulation to achieve a zero pressure-gradient boundary layer. The computational grid, boundary conditions, as well as the inflow turbulent boundary layer are the same as for the neutrally buoyant case described by Tomas et al. (2016), in which further details are given.

2.3.3 Statistics

The simulations with a turbulent inflow started from a statistically steady solution generated with a steady mean inflow profile. A constant timestep of 0.0156T was used, where $T=h/U_h$ and $U_h$ is a velocity scale defined in the next section. The simulations ran for at least 780T before statistics were computed, which was long enough to assure a steady state. Statistics were computed for a duration of at least 780T with a sampling interval of 0.31T resulting in converged results. This duration corresponds to approximately 125 uncorrelated samples in the experiment. The simulations were well-resolved, such that the average subgrid stress $\overline{-2\nu _\mathrm{sgs}S_{13}}$ did not exceed 6% of the total Reynolds stress, as shown in Tomas et al. (2016). Therefore, only the resolved statistics are shown in the subsequent sections.

Table 1 Summary of the properties of the approaching boundary layer; $\delta ^*$ is the displacement thickness, $\theta$ is the momentum thickness, and H is the shape factor

Fig. 3

Properties of the approaching flow: mean flow speed $\overline{u}$ (a), r.m.s. of the fluctuating velocity components (b), and Reynolds stress $-\overline{u'w'}$ (c). The circle indicates $U_h\equiv \overline{u}|_{z=h}$. The errorbars represent the statistical mean ± the standard error of the mean

3 Results: Flow Statistics

3.1 Approaching Flow Conditions

The characteristics of the approaching flow boundary layer have an influence on the flow development over obstacles (Castro 1979; Blackman et al. 2015). Therefore, here a comparison is given of the approaching flow boundary layer in the experiments and in the simulations. A summary of the relevant boundary-layer properties for both the experiments and the simulations can be found in Table 1. All profiles are normalized with the velocity at obstacle height at the start of the measurement/simulation domain (in absence of the urban array), $U_h\equiv \overline{u}|_{z=h}$, which proved to be the best scaling for the rural-to-urban flows discussed in the subsequent sections. However, it should be kept in mind that h and $U_h$ are not the length scale and velocity scale for smooth-wall turbulent boundary layers, since normally $\delta$ and $U_\infty$ are used. Therefore minor discrepancies are found when comparing the two methods.

Figure 3 depicts the velocity profile, the profiles of the root-mean-square (r.m.s.) of the velocity fluctuations, and the mean Reynolds stress distribution in the vertical direction for the experiments and the LES. Despite the different ways of generating the approaching boundary layer there is a satisfactory agreement between the results of the two methods; a good match is found for the mean velocity profile in the range $0\le z/h\le 3$ (Fig. 3a). In the LES a zero pressure-gradient boundary layer was generated, while in the experiment a slightly favourable pressure gradient was present due to the boundary-layer growth and the constant cross-sectional area of the tunnel. With the normalization with $U_h$ this difference adds to a lower streamwise velocity component in the outer region (above $z/h=3$) of the experimental boundary layer. As observed in Fig. 3b the profiles of $u_\text {rms}$ and $w_\text {rms}$ are similar in shape when comparing the experimental data with the LES simulations. The main differences are attributed to the difference in predicted and measured $U_h$ (see Table 1), i.e. the lower $U_h$ in the LES causes the scaled velocity fluctuations to be larger than in the experiments. In addition, the small favourable pressure gradient in the experiments reduces the velocity fluctuations in the experimental boundary layer (Joshi et al. 2014). Furthermore, a reduction is observed in the mean Reynolds stress in the experiments in the region $2\le z/h \le 5$, see Fig. 3c. This is most likely attributed to the design and the arrangement of the spires. Nevertheless, as will be shown in the subsequent sections, the differences in characteristics of the approaching flow did not cause significant discrepancies in the development of the flow over the urban canopy.

The Reynolds number (Re), based on $U_\infty$ and h, was approximately $5.0\times 10^3$ for both the numerical simulations and the experiments, which is in the regime where Reynolds number effects are small when flow over sharp-edged obstacles is considered (Cheng and Castro 2002b). In addition, the wall-friction Reynolds number ($h^+$), based on $u_{\tau }$ and h, was around 200 in both cases, which is slightly above the lower limit of $h^+\approx 100$ for dynamically fully rough flow (Raupach et al. 1991).

Fig. 4

Contours of instantaneous spanwise velocity component $v/U_h$ in the midplane of case AR5; a experiment and b simulation. Areas that could not be illuminated or seen in the experiments have been masked in grey and the obstacles are shown in white

Fig. 5

Contours of mean streamwise velocity component $\overline{u}/U_h$ (a, b) and mean vertical velocity component $\overline{w}/U_h$ (c, d) in the midplane of case AR5; experiment (a, c) and simulation (b, d). Areas that could not be illuminated or seen in the experiments have been masked in grey and the obstacles are shown in white

Fig. 6

Contours of $\overline{u'u'}/U^2_h$ (a, b) and $\overline{u'w'}/U^2_h$ (c, d) in the midplane of case AR5; experiment (a, c) and simulation (b, d). Areas that could not be illuminated or seen in the experiments have been masked in grey and the obstacles are shown in white

3.2 The Flow Over the Urban Canopy

In this section the acquired rural-to-urban flow fields are compared for the first eight streets in the $y=0$ plane, see Fig. 1. All velocity statistics are normalized with the undisturbed velocity at obstacle height $U_h$. A snapshot of the spanwise velocity component is shown in Fig. 4 for case AR5 for both the experiment and the simulation. The results show similar large turbulent structures arising from the top of the obstacles, which grow in downstream direction and that have a larger magnitude than the velocity fluctuations in the approaching flow. Figure 5 visualizes the effect of the roughness transition on the mean flow. It shows the contour plots of the mean streamwise velocity component $\overline{u}$ as well as the mean vertical velocity component $\overline{w}$ for case AR5. As the results were averaged over a duration of the order of $10^3T$, the statistics were converged to within a few percent. The differences in $\overline{u}$ and $\overline{w}$ between the simulations and the experiments are mostly smaller than that, indicating that the agreement is very good. The only significant difference is the size of the mean recirculation areas at the top of the first three rows of obstacles. The LES predicts a negative vertical velocity close to the downstream walls of the first two street canyons, while in the experiment the flow is solely directed out of the street canyons. This difference can be caused by a limitation of the employed methods; especially at the top of the first obstacle the PIV/LIF results should be interpreted with care, because due to high spatial gradients of the velocity and reflections from the obstacle, the PIV results in this region are prone to errors. In this region, too, the numerical errors in the LES can be expected to be largest due to the high velocity near the singularity at the obstacle corners and the large change in velocity gradients. However, these differences could also be purely physical, since the slightly different turbulence characteristics in the approaching flow (see Sect. 3.1) can influence the development of the shear layer emanating from the first obstacle (Castro 1979; Blackman et al. 2015). Nevertheless, downstream of the third row the results of the two methods are nearly indistinguishable.

Fig. 7

Profiles of mean streamwise velocity component $\overline{u}/U_h$ in the middle of each street canyon for cases AR1 (a), AR2 (b), AR5 (c), AR8 (d), and 2D (e). The internal boundary-layer depth, $\delta _i$, is shown by solid markers for the LES and by open markers for the experiment (if available)

Figure 6 shows the mean Reynolds stresses $\overline{u'u'}$ and $-\overline{u'w'}$ for the same case. The strong shear layer emanating from the upstream corner of the first obstacle generates large turbulent fluctuations resulting in a peak in $\overline{u'u'}$ above the first obstacle and a peak in $-\overline{u'w'}$ above the first street canyon. The flow appears to be also strongly affected by the presence of the second obstacle, above which another peak in $\overline{u'u'}$ is present, while a peak in $-\overline{u'w'}$ is located above the second street canyon. The intensity of the turbulent plume decreases in downstream direction, while weaker plumes of $-\overline{u'w'}$ are produced by the shear layers above the street canyons. Just as for $\overline{u}$ and $\overline{w}$ there are some discrepancies between the experiments and the simulations above the first three obstacle rows due to the aforementioned reasons. The contour plots in Figs. 5 and 6 give an overall view of the flow and can be used for a qualitative comparison of the two methods. Figure 7 allows for a quantitative comparison of cases AR1, AR2, AR5, AR8, and 2D, by showing the vertical profiles of the mean streamwise velocity component 0.5h in front of the first obstacle row and in the middle of each subsequent street canyon. The LES data are shown by continuous lines, while, if available, the experimental data are shown by dashed lines. In all cases backflow occurred inside the canopy, while above the canopy an internal boundary layer developed, which is defined and discussed in Sect. 3.3 and shown in Fig. 7 by open symbols for the experiment and by solid symbols for the LES. In all cases the flow profiles in the street canyon changes significantly over the first three to four rows of obstacles while only minor changes are observed from street canyon 4 onwards. For case AR1, and especially case AR2, $\overline{u}$ is mostly negative at this location in the street canyon, while for cases AR5, AR8, and 2D a ‘canyon vortex’ arises that is most apparent in case 2D.

Figure 8 shows the profiles of the mean Reynolds stress $-\overline{u'w'}$ at the same locations. The differences between the LES and the experiments are minor with the maximum differences occurring in the region with large gradients just above the canopy in the first street canyon. In this region the finite resolution of the PIV acts as a lowpass filter, which results in an underestimation of the peak value of the Reynolds stresses. The fraction of resolved Reynolds stresses can be estimated from the ratio between the PIV resolution and the length scale $\varLambda$ of the dominating flow structures (Scarano 2003). $\varLambda$ is estimated using the distance required for the streamwise two-point correlation of u to decrease to 0.5. Above the first street canyon in case AR8 (Fig. 8d) $\varLambda$ is 0.3h, resulting in approximately 83% of the Reynolds stress being resolved at that location.

Fig. 8

Profiles of mean Reynolds stress $-\overline{u'w'}/U^2_h$ in the middle of each street canyon for cases AR1 (a), AR2 (b), AR5 (c), AR8 (d), and 2D (e). The internal boundary-layer depth, $\delta _i$, is shown by solid markers for the LES and by open markers for the experiment (if available)

With increasing aspect ratio l / h the blockage of the incoming flow increases, which results in an increase of the peak in $-\overline{u'w'}$ behind the first row of obstacles. Further downstream this peak diffuses, and eventually the largest value of $-\overline{u'w'}$ occurs near the top of the canopy, where the rooftop shear layers are the largest sources of turbulence production. In view of blockage of the flow case AR8 approximates the 2D case, which is reflected in a similar peak in $-\overline{u'w'}$ behind the first row. However, in the eighth street canyon the depth of the region with increased Reynolds stress is larger for case AR8 than case 2D. This is because the three-dimensional roughness arrays (all cases other than 2D) induce a secondary flow that causes the internal boundary layer to grow more rapidly in case AR8 than in case 2D. This is further discussed in Sect. 3.3.

Furthermore, since the Reynolds stress induced by the first row of obstacles is more than ten times larger than the Reynolds stress in the approaching flow boundary layer, the influence of the slight difference in approaching flow characteristics between experiments and simulations is marginal.

Fig. 9

Surface drag and resulting internal boundary layer; a mean street-averaged friction velocity $u_\tau$, b mean street-averaged displacement height d (LES only), c fully-developed d and displacement height $d^*$ found by fitting with the logarithmic velocity profile (LES only), d roughness length $z_0$ found by fitting with the logarithmic velocity profile (LES only), e internal boundary-layer depth $\delta _i$

3.3 Surface Forces and Internal Boundary-Layer Growth

To investigate the effect of the roughness transition on the boundary layer the change in drag is quantified by considering the total drag force for each street area $A_\text {street}$, which has a length of 2h and a width equal to the domain size. The total drag force consists of skin frictional drag, $F_\tau$, and form drag, $F_p$;

$$\begin{aligned} F_\tau= & {} \int _{A_\text {s}} \overline{\tau }\, \mathrm{d}A, \end{aligned}$$

(4)

$$\begin{aligned} F_p= & {} \int _{A_\text {f}} \mathrm {\Delta }\overline{p}\, \mathrm{d}A, \end{aligned}$$

(5)

where $\overline{\tau } = \rho \nu \left( \partial \overline{u}/\partial n\right) _0$ is the mean wall shear stress, $\rho$ is the fluid density, $A_\text {s}$ is the total area of all surfaces in each street (i.e. the top and side faces of the obstacles as well as the ground surface), $\mathrm {\Delta }\overline{p}$ is the mean pressure difference between upwind and downwind faces of the obstacles, and $A_\text {f}$ is the frontal area of the obstacles in each street. At the 23rd street $F_p$ constituted around $75\%$ of the total drag, which means the viscous drag cannot be neglected at this Reynolds number. In Fig. 9a the streamwise development of the total drag is shown for the simulations in the form of the friction velocity $u_\tau =\left[ \left( F_\tau +F_p\right) /\left( \rho A_\text {street}\right) \right] ^{1/2}$. In the experiments the forces on the obstacles and on the ground plate were not measured, so $u_\tau$ could not be computed. In fully-developed conditions and under the assumption that the viscous drag is negligible, $u_\tau$ can be estimated from the spatially-averaged value of $\overline{u'w'}$ near the top of the canopy (Cheng and Castro 2002b). For the LES results this method indeed approximates the form drag contribution to $u_\tau$ to within $4\%$ when the last street (23rd) is considered. For the experimental results $\overline{u'w'}$ is only available in the midplane and up to the eighth street. The estimation $u_\tau \approx (-\langle \overline{u'w'}\rangle )^{1/2}$, where $\langle \overline{u'w'}\rangle$ is the streamwise-averaged Reynolds stress near the top of the obstacles, is shown in Fig. 9a by the red, blue, and green ✩ symbols for case AR1, AR5, and AR8, respectively. The difference of approximately 20 % compared to the LES results is mainly attributed to not taking into account the viscous contribution. However, spanwise variations in $-\overline{u'w'}$ are also a possible source of discrepancy, as will be discussed later. Figure 9b shows the streamwise development of the displacement height d, which is the height at which the total drag force acts (Jackson 1981). It is computed by dividing the total moment of the drag forces by the total drag force. After approximately nine streets d has reached a constant value, where the cases with highest blockage need longest distance to adapt. Moreover, it can be seen that with increasing l / h, d increases to the maximum of nearly h for case 2D.

Near-surface flows over rough surfaces are commonly parametrized using the logarithmic velocity profile

$$\begin{aligned} \overline{u} = \frac{u_\tau }{\kappa }\text {ln}\left( \frac{z-d^*}{z_0}\right) , \end{aligned}$$

(6)

where $\kappa$ is the von Kármán constant ($\kappa =0.4$), $z_0$ is the roughness length, and $d^*$ is the displacement height, which is written with the superscript $^*$ to show that it differs from d; both $d^*$ and $z_0$ are found by fitting the velocity profile from the LES to Eq. (6), while d follows directly from the force balance. In Fig. 9c both d and $d^*$ are plotted for the 23rd street for all cases, showing a discrepancy that has also been reported by Cheng and Castro (2002b) and Cheng et al. (2007). They suggest that this difference arises from either a different value for the von Kármán constant or significant dispersive stresses within the canopy. The latter is confirmed by a DNS investigation by Coceal et al. (2006). Figure 9d shows $z_0$ for all cases at the same location from which it can be concluded that, except for case AR2, $z_0$ decreases with increasing aspect ratio, which is in agreement with earlier studies that show that for cubical roughness $z_0$ decreases for $\lambda \gtrsim 0.2$ (Macdonald et al. 1998). Nevertheless, from Fig. 9a, c, d it is clear that case AR2 induces the largest drag force and that, unlike the other cases, this drag force has not yet fully developed. In addition, at the end of the domain the velocity profile for case AR2 showed only a small logarithmic region, most likely because it was still developing.

The effect of the change in surface drag on the mean velocity is shown in Fig. 9e, where the internal boundary-layer depth $\delta _i$ is given for each street for both the experiments and the simulations; $\delta _i$ is found by subtracting the smooth-wall inlet velocity profile from the mean velocity field for the roughness transition: $\mathrm {\Delta } \langle \overline{u}\rangle = \langle \overline{u}\rangle _{\text {RT}} - \langle \overline{u}\rangle _{\text {inlet}}$. Here, $\delta _i$ is defined as the height at which the vertical gradient of $\mathrm {\Delta } \langle \overline{u}\rangle$ reaches zero, and the threshold $\left| \mathrm {d\Delta }\overline{u}/\mathrm {d}z\right| < 0.005 U_h/h$ was used to determine this location. There is a good match between the experiments and the simulations; initially $\delta _i$ grows more rapidly for larger aspect ratios. However, the depth $\delta _i$ does not solely depend on the blockage of the flow; secondary flows generated by the three-dimensional roughness geometry also affect the internal boundary-layer growth. This is indicated by the fact that $\delta _i$ is slightly larger for case AR8 than for case 2D, while the blockage of the flow is less. The secondary flow is found in all cases, except case 2D, and starts after the first row of obstacles. It is visualized in Fig. 10 by vectors of mean velocity in the plane $x/h=44.5$ (the upstream side of street 23) for cases AR1, AR2, AR3.5, and AR5. The contours of $-\overline{u'w'}/U^2_h$, plotted in the same figure, show that the secondary flow influences the distribution of $-\overline{u'w'}$. This inhomogeneity can reach up to the internal boundary-layer depth depending on the l / h ratio. For all cases the contours show spanwise variations that correspond with the size of the repeating element. Local upwash and downwash regions can be identified. These are of largest magnitude in case AR2, resulting in two counter-rotating streamwise vortices that reach up to 2h above the canopy. We hypothesize that the strength of the secondary flow, and thus the increase in drag, is largest when the spanwise spacing of the roughness elements is roughly proportional to $\delta _i - h$. This is analogous to the conclusion by Vanderwel and Ganapathisubramani (2015), who experimentally measured a fully-developed boundary layer with a depth of 11.3h and found that large-scale secondary flows are accentuated when the spanwise spacing of roughness elements is roughly proportional to the boundary-layer depth. Finally, it must be noted that the presence of large-scale secondary flows requires spatial averaging of $-\overline{u'w'}$ over regions of at least the size of the repeating element in order to derive an accurate estimate of $u_\tau$. The experimental results in Fig. 9a are based on a spatial average in the midplane only. Fortunately, as shown in Fig. 10, the spanwise variation of $-\overline{u'w'}$ is relatively small for these cases (AR1, AR5, and AR8).

Fig. 10

Visualization of secondary flow by mean velocity vectors in the $y-z$ plane at $x/h=44.5$ (the upstream side of street 23) for cases AR1, AR2, AR3.5, and AR5. The contours show the mean resolved Reynolds stress $-\overline{u'w'}/U^2_h$

4 Results: Pollutant Dispersion

Pollutant dispersion was investigated by considering concentrations of a passive tracer released from a line source 2h upstream of the urban canopy. The concentrations $c^*$, retrieved both from measurements and from simulations, are non-dimensionalized using the reference velocity $U_h$, obstacle height h, source width $L_y$, source concentration $c_\text {s}$, and source volume flow rate $\phi _\text {s}$ (see Sect. 2.2.3),

$$\begin{aligned} c=\frac{c^* U_h h L_y}{c_\text {s}\phi _\text {s}}. \end{aligned}$$

(7)

Figure 11 shows the contours of c for case AR5 corresponding to the instantaneous velocity field shown in Fig. 4. The experimental results exhibit more distinctive layers than the simulations due to the larger Schmidt number (Sc). Nevertheless, there is a high degree of similarity when the larger structures are considered. This is reflected in a turbulent Schmidt number of 1.21 in the experiments and 0.77 in the LES, which was estimated by deriving the turbulent viscosity and the turbulent diffusivity using the ‘Boussinesq approximation’.

Fig. 11

Contours of instantaneous concentration c (defined in Eq. 7) in the midplane of case AR5; a experiment and b simulation. The snapshots correspond to the velocity fields shown in Fig. 4. Areas that could not be illuminated or seen in the experiments have been masked in grey and the obstacles are shown in white

4.1 Mean Concentration Fields

Figure 12a–d shows the vertical distribution of mean concentration starting 0.5h upstream of the first row of obstacles and in the middle of each subsequent street canyon for cases AR1, AR5, AR8, and 2D. The LES data are shown by continuous lines, while, if available, the experimental results are shown by the dashed lines. The internal boundary-layer depth $\delta _i$ is plotted by solid markers for the LES and by open markers for the experiment. Clearly, the vertical profiles for $\overline{c}$ are largely controlled by $\delta _i$ as high concentrations remain inside the internal boundary layer. The most pronounced differences between the numerical and experimental results are observed inside and just above the street canyons (i.e. $z/h<1.5$), where the experiments indicate a significantly higher concentration. Additional tests revealed that the line source was slightly non-uniform in spanwise direction with a higher than average flow rate at the location of the measurement plane. Nevertheless, the average flow rate through the line source was kept constant in time. The influence of the spanwise non-uniformity decreases in downstream direction as turbulence decreases this lateral inhomogeneity, leading to a closer match between the two methods further downstream. This behaviour is also reflected in Fig. 12e, where the average street-canyon concentration is shown. Since the street canyon is not completely visible in the experimental results, the average street-canyon concentration is determined only in the upper part of the street canyon. From the LES results it is concluded that this is a good approximation, as the street-canyon concentration is quite uniform (especially in the more downstream street canyons). Considering the different aspect ratios it is clear that cases AR5, AR8, and 2D predict qualitatively similar behaviour: the maximum average concentration occurs in the first street and the average concentration decreases slowly in subsequent streets. Different behaviour is found in the AR1 case, where the street-canyon concentration is lower in the first street and subsequently reaches its maximum in the third street canyon. This is because for case AR1 a large part of the concentration is advected with high velocity through the streamwise streets, thereby passing the first two street canyons. As the flow velocity has decreased after two streets, the concentration in the wakes of the cubes increases.

Fig. 12

Profiles of mean concentration $\overline{c}$ in the middle of each street canyon for cases AR1 (a), AR5 (b), AR8 (c), 2D (d), and spatially-averaged street-canyon concentration $\langle \overline{c}\rangle$ (e). In frames a–d the internal boundary-layer depth, $\delta _i$, is shown by solid markers for the LES and by open markers for the experiment (if available)

Fig. 13

Streamwise variation of the advective and turbulent pollutant fluxes for different aspect ratios (a) and spatial variation of advective and turbulent pollutant fluxes for the 5th street of case AR8 (b). Red, green, and blue lines/symbols correspond to cases AR1, AR5, and AR8, respectively; $x'=0$ corresponds to the upstream street-canyon wall

4.2 Pollutant Dispersion Mechanisms

The geometry of the urban canopy has an influence on the dispersion of pollutants (Belcher 2005); e.g. in the currently considered geometries pollutants can travel with the mean flow through streamwise streets or above the urban canopy. Sometimes pollutants get trapped inside the wakes of the obstacles, and since the considered cases are in the skimming flow regime these wakes form street-canyon flows. Pollutants leave the street canyons mostly through the top of the canopy either by being advected with the mean flow or by turbulent velocity fluctuations. Therefore, the average total pollutant flux in the midplane of each street canyon is

$$\begin{aligned} \overbrace{\langle \overline{wc}\rangle _{z=h}}^ I = \overbrace{\langle \overline{w}\,\overline{c}\rangle _{z=h}}^ II +\overbrace{\langle \overline{w'c'}\rangle _{z=h}}^ III , \end{aligned}$$

(8)

where the total average pollutant flux (I) consists of a contribution of advection (II), and a contribution of turbulence (III). In addition, the $\langle ..\rangle |_{z=h}$ symbols represent the average over the region $\left( 0.05<\right.$ $x'/h$ $< 0.95$, $0.95<$ $z/h<$ $\left. 1.05\right)$, where $x' = 0$ represents the location of the upstream wall of the street canyon. Note that the averaging region is taken slightly smaller than the street-canyon width to avoid errors introduced by wall reflections in the experiments. Figure 13a shows the streamwise development of both contributions. Clearly, in the first three streets the advective pollutant flux is significant. Remarkably, case AR1 shows a negative advective pollutant flux both in the experiment and in the LES, in contrast to the spanwise-averaged result (as in Tomas et al. 2016). This indicates that the three-dimensionality of the flow causes the advective pollutant flux in the midplane of the obstacles to be opposite to the spanwise-averaged result, which is positive because the mean spanwise-averaged vertical velocity is positive. Furthermore, the experimental and LES results for the average advective flux are approximately the same, except for case AR5, where the experimental results show a much larger average advective flux from the first three street canyons. This is mostly related to the difference in vertical velocity at these locations (as was discussed in Sect. 3.2 and shown in Fig. 5) and partly due to the larger mean concentration. Furthermore, Fig. 13b shows the spatial distribution of $\overline{w}\,\overline{c}$ and $\overline{w'c'}$ at the top of street 5 of case AR8. The shapes of these profiles are similar from street 4 and onwards. The agreement between the experiment and the LES is good; for the simulation $\overline{w}\,\overline{c}$ shows wiggles that are characteristic for simulations of flow near sharp obstacle corners when using central-differencing for the advection terms in the momentum equations. However, the local values of $\overline{w}$ are relatively small and the agreement with the experiment is satisfactory. It is found that, similar to Michioka et al. (2014), $\overline{w'c'}$ is always positive at the top of the canopy, i.e. turbulence always acts to remove pollutants from the street canyons.

Fig. 14

Joint probability density function (p.d.f.) of the streamwise velocity fluctuation $u'$ and instantaneous vertical pollutant flux wc multiplied with the associated value of wc; the results are averaged over the region $\left( 0.05<\right.$ $x'/h$ $< 0.95$, $0.95<$ $z/h<$ $\left. 1.05\right)$ for street 6; a AR1, b AR5, c AR8, d 2D; the line contours show the experimental results and the coloured contours show the LES results

To investigate under which conditions pollutants are ventilated from street canyons, the joint probability density function (p.d.f.) of streamwise velocity fluctuation $u'$ and instantaneous vertical pollutant flux wc was computed in each street in the region $\left( 0.05<\right.$ $x'/h$ $< 0.95$, $0.95<$ $z/h<$ $\left. 1.05\right)$, where $x' = 0$ represents the location of the upstream wall of the street canyon. The shape of the joint p.d.f. does not vary significantly inside this region. Therefore, the joint p.d.f. is averaged over this region and shown for street 6 for cases AR1, AR5, AR8, and 2D in Fig. 14, where the joint p.d.f. has been multiplied with the associated value of wc to visualize the contribution to the total average pollutant flux $\overline{wc}$. For all cases the pollutant flux wc is mainly negative when $u'>0$ , i.e. pollutants enter the street canyon from above, while for $u'<0$ the pollutant flux wc can be either positive or negative. It is found that after three streets the joint p.d.f.s have the same shape as shown in Fig. 14, which suggests the dominating mechanism responsible for pollutant removal has developed after three streets. Accordingly, in (periodic) simulations of fully-developed flow over street canyons qualitatively similar joint p.d.f.s are found (Michioka et al. 2014). From the results presented here it can be concluded that ventilation of street canyons is associated with low momentum regions passing the street canyons.

4.2.1 The Mean Fluctuating Velocity Field for Street-Canyon Ventilation

Apart from the knowledge that low momentum regions are responsible for street-canyon ventilation, details about the associated flow structure are unknown. Reynolds and Castro (2008) and Michioka et al. (2011) investigated the occurrence of sweeps and ejections in the urban canopy by computing two-point correlations of u. However, the direct correlation between street-canyon ventilation and the flow was not made. Here, use is made of linear stochastic estimation (Adrian 1988) to approximate the conditional mean velocity fluctuation for the event of a pollutant flux $\langle wc \rangle _\text {e}$ out of the street canyon: $\overline{u'_i(\varvec{x})|\langle wc\rangle _\text {e}}$, where $\varvec{x}=(x,y,z)$ and $\langle ..\rangle$ represents the spatial average over the region $\left( 0.05<\right.$ $x'/h$ $< 0.95$, $0.95<$ $z/h<$ $\left. 1.05\right)$ in the midplane of the obstacles. Analogously to Christensen and Adrian (2001) this conditional mean is approximated by

$$\begin{aligned} \overline{\left. u'_i\right. ^ e }=\overline{u'_i(\varvec{x})|\langle wc\rangle _\text {e}} \approx \frac{\overline{\langle wc \rangle u'_i(\varvec{x})}}{\overline{\langle wc \rangle ^2}}\langle wc \rangle _\text {e}, \end{aligned}$$

(9)

which shows that the mean fluctuating velocity field associated with a given value of $\langle wc \rangle _\text {e}$ can be reconstructed using unconditional two-point correlation data. Linear stochastic estimation is more practical than the conventional conditional-averaging procedure, because all available samples are used in reconstructing the conditional fluctuating velocity field, so that fewer samples are required for converged results. As the amplitude of $\overline{\left. u'_i\right. ^ e }$ depends (linearly) on the chosen magnitude of $\langle wc \rangle _\text {e}$ a realistic event is chosen to compare with. Figure 14 shows that the event of $\langle wc \rangle _\text {e} = 0.1U_h\langle \overline{c}\rangle$ occurs frequently in all considered cases. Therefore, this will be the event for which the considered roughness geometries are compared. Figure 15 shows for cases AR1 and AR8 the vector field of the fluctuating velocity $\overline{\left. u'_i\right. ^ e }$ together with contours of $\overline{\left. u'\right. ^ e }$ found by using Eq. (9). The experimental data are shown for street 6, but from street 5 and onwards the structure does not change significantly. Therefore, for the LES the data have been averaged over streets 6 to 21 for statistical convergence. As expected from the joint p.d.f.s, low momentum flow is indeed present above the canopy during the ventilation event, which is indicated by the contours of negative $\overline{\left. u'\right. ^ e }$. The agreement between the results from the experiment and the LES is good; in the proximity of the top of the street canyon the contours are very similar, while the contours further away have a slightly different shape. Nevertheless, both methods predict a flow structure of greater length and height for case AR8 than for case AR1. To indicate the influence of the aspect ratio on the size of these regions the streamwise length scale $\mathcal {L}_x$ and the vertical length scale $\mathcal {L}_z$ of the contour $\overline{\left. u'\right. ^ e }=-0.04U_h$ are plotted in Fig. 16, where $\mathcal {L}_x$ is the length of the contour just above the canopy and $\mathcal {L}_z$ is the maximum height of the contour above the canopy. Using a different value for the contour did not show significantly different behaviour. Figure 16 indicates that increasing the aspect ratio mostly affects $\mathcal {L}_z$, which increases linearly. The relative increase is significant, which is evident from Fig. 15. Surprisingly, $\mathcal {L}_z$ is lower for the 2D case. The results for the streamwise length scale $\mathcal {L}_x$ (Fig. 16a) do not show a clear trend, because there is less agreement between the experimental and numerical results, and because the differences in $\mathcal {L}_x$ relative to the average value of $\mathcal {L}_x$ are smaller than for $\mathcal {L}_z$.

Fig. 15

Mean fluctuating velocity field $\overline{\left. u'_i\right. ^ e }$ associated with $\langle wc \rangle _\text {e}= 0.1U_h\langle \overline{c}\rangle$ from linear stochastic estimation for case AR1 (a, b) and case AR8 (b, d). Contours of $\overline{\left. u'\right. ^ e }/U_h$ are shown together with the vector field $(\overline{\left. u'\right. ^ e },\overline{\left. w'\right. ^ e })$ in the $y=0$ plane for the experiments in street 6 (a, c), while for the LES the average result of street 6 to street 21 is shown (b, d). The average streamwise location of the event is indicated by $x^*$

Fig. 16

Length scales of the contour $\overline{\left. u'\right. ^ e }=-0.04U_h$ in the plane $y=0$ for different aspect ratios l / h; a streamwise length just above the canopy $\mathcal {L}_x$ and b maximum height above the obstacles $\mathcal {L}_z$

Figure 15 illustrates the average instantaneous flow field associated with street-canyon ventilation in the $y=0$ plane, but what happens inside the urban canopy during such an event? From the simulations $\overline{\left. u'_i\right. ^ e }$ can also be retrieved in the horizontal plane in the urban canopy, which is shown in Fig. 17 for the plane $z/h=0.5$. Although the contours of $\overline{\left. u'\right. ^ e }$ in Fig. 15 indicate that the correlation of $\overline{\left. u'\right. ^ e }$ with $\langle wc\rangle _\text {e}$ decreases significantly when considering locations inside the street canyon, $\overline{\left. w'\right. ^ e }$ inside the street canyon does correlate with $\langle wc\rangle _\text {e}$ (as is evident from the length of the vectors). In Fig. 17 $\overline{\left. w'\right. ^ e }$ is shown by the contours, while $\overline{\left. u'\right. ^ e }$ and $\overline{\left. v'\right. ^ e }$ are shown by the vectors. Cases AR1 and AR2 clearly show a horizontal inflow from the adjacent streamwise streets and even from the neighbouring street canyons to balance the outflow at the top the street canyon. For these cases the region of positive $\overline{\left. w'\right. ^ e }$ even extends around the obstacle. In the other cases (AR3.5, AR5, AR8, and 2D) outflux in the middle of the top of the street canyon is balanced by inflow within the region of the street canyon itself, such that the velocity fluctuation field looks similar for cases AR3.5 to 2D. The contours of $\overline{\left. w'\right. ^ e }$ indicate that in all cases the event influences the flow in one or two upstream street canyons.

Fig. 17

Mean fluctuating velocity field $\overline{\left. u'_i\right. ^ e }/U_h$ associated with $\langle wc \rangle _\text {e} = 0.1U_h \langle \overline{c}\rangle$ from linear stochastic estimation for cases AR1 (a), AR2 (b), AR3.5 (c), AR5 (d), AR8 (e), and 2D (f). Contours of $\overline{\left. w'\right. ^ e }/U_h$ are shown together with the vector field $(\overline{\left. u'\right. ^ e },\overline{\left. w'\right. ^ e })$ in the $z/h=0.5$ plane. The average result of street 6 to street 21 is shown, while use is made of symmetry. The average streamwise location of the event is indicated by $x^*$

5 Conclusions

Large-eddy simulations as well as simultaneous PIV and LIF measurements were employed to investigate flow and pollutant dispersion behaviour in regions where the surface changes from rural to urban type roughness. The influence of the aspect ratio of the obstacles, which make up the urban canopy, was investigated for the case of approaching flow over a smooth wall at a roughness Reynolds number, $h^+$, of 194 for the simulations and 213 for the experiments. The results show that the two methods independently predict practically the same velocity statistics. Furthermore, minor differences in the region of the first row of obstacles can be attributed to the accuracy of both methods and slight differences in the generated smooth-wall boundary layers. The concentration statistics show some differences at the start of the canopy due to a slight non-uniformity in the emission source in the experiment. Nevertheless, qualitatively there is a good agreement between the methods, and the same dispersion mechanisms are identified.

The force balance from the simulations shows that for all cases, except one, after approximately eight streets the surface forces have adapted to the surface roughness. However, for $l/h=2$ the surface forces are still developing at $x=46h$ (which is the end of the considered numerical domain) due to the occurrence of large-scale secondary flow. As a consequence, the roughness length $z_0$ and the displacement height $d^*$, as used in the standard logarithmic law, are discontinuous when plotted against l / h. It is hypothesized that this phenomenon occurs because for $l/h=2$ the spacing of the roughness elements is proportional to $\delta _i-h$, analogous to conlusions by Vanderwel and Ganapathisubramani (2015). As to whether or not this large-scale secondary flow eventually disappears, as the internal boundary layer grows, remains an open question. Nonetheless, it is concluded that estimating $u_\tau$ by using $\overline{u'w'}$ from single plane measurements only, can be inaccurate due to the spanwise variation caused by this secondary flow. In addition, it is found that with $l/h>2$ the surface drag decreases as the flow is characterized to a larger extent by the skimming flow regime.

The effect of the roughness transition on pollutant dispersion is that the mean vertical pollutant flux at the top of the street canyons is dominated by the advective pollutant flux $\overline{w}\,\overline{c}$ in the first three streets, after which the profiles of $\overline{w}\,\overline{c}$ and $\overline{w'c'}$ along the streamwise extent of the street canyons become similar to those for the fully-developed cases described by Michioka et al. (2014). Likewise, the joint p.d.f.s of the streamwise velocity fluctuation $u'$ and the instantaneous vertical pollutant flux wc have a comparable shape from the fourth street onwards. In addition, it is found that, in agreement with Michioka et al. (2014), the joint p.d.f.s are qualitatively similar for all considered l / h, showing that street canyon ventilation of pollutant is mostly associated with $u'<0$.

Subsequently, the flow structure that is responsible for street-canyon ventilation was identified by means of linear stochastic estimation. It is found that for larger l / h street-canyon ventilation is associated with larger regions of $u'<0$, and that their vertical length scale increases linearly with increasing l / h. However, the result for the 2D case does not result in the largest structure. In addition, during such a ventilation event the flow structure inside the urban canopy shows more variation in the horizontal plane for $l/h=1$ and $l/h=2$ than for larger aspect ratios, for which the variation is confined mostly to the considered street canyon.