Abstract
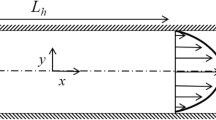
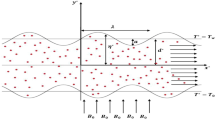
Continuous nutrient delivery to cells by pressure-driven flow is desirable for cell culture in lab-on-a-chip devices. An innovative method is proposed to generate an induced pressure-driven flow by using an electrokinetically-driven pump in a H-shape microchannel. A three-dimensional numerical model is developed to study the effectiveness of the proposed mechanism. It is shown that the average velocity of the generated pressure-driven flow is linearly dependent on the applied voltage. Considering the culture of a multicellular tumour spheroid (MTS) in such a microfluidic system, numerical simulations based on EMT6/Ro tumour cells is performed to find the effects of the nutrient distribution (oxygen and glucose), bulk velocity and channel size on the cell growth. Using an empirical formula, the growth of the tumour cell is studied. For low nutrient concentrations and low speed flows, it is found that the MTS grows faster in larger channels. It is also shown that, for low nutrient concentrations, a higher bulk liquid velocity provide better environment for MTS to grow. For lower velocities, it is found that the local MTS growth along the flow direction deviates from the average growth.












Similar content being viewed by others
References
R.P. Araujo, D.L.S. McElwain, Bull Math Biol 66, 1039 (2004)
K. Bartha, H. Rieger, J Theor Biol 241, 903 (2006)
H.M. Byrne, T. Alarcon, M.R. Owen, S.D. Webb, P.K. Maini, Phil Trans R Soc A 364, 1563 (2006)
J.J. Casciari, S.V. Sotirchos, R.M. Sutherland, Cell Prolif 25, 1 (1992)
P.P. Delsanto, C. Guiot, P.G. Degiorgis, C.A. Condat, Y. Mansury, T.S. Deisboeck, Appl Phys Lett 85, 4225 (2004)
J.P. Freyer, J Cell Physiol 76, 138 (1998)
J.P. Freyer, R.M. Sutherland, J Cell Physiol 124, 516 (1985)
W. Gu, X. Zhu, N. Futai, B.S. Cho, S. Takayama, Proc Natl Acad Sci USA 101, 15861 (2004)
G. Hu, D. Li, Biomed Microdevices 9, 315 (2007)
J.M. Kelm, N.E. Timmins, C.J. Brown, M. Fussenegger, L.K. Nielsen, Biotechnol Bioeng 83, 173 (2003)
J. Landry, J.P. Freyer, R.M. Sutherland, Cell Tissue Kinet 15, 585 (1982)
C.K.N. Li, cancer 50, 2066 (1982)
D. Li, Electrokinetics in Microchannels (Elsevier, 2004)
R.H. Perry, Perry’s chemical engineers’ handbook, 6th edn. (McGrwa-Hill, New York, 1984)
K.A. Rejniak, J Theor Biol 247, 186 (2007)
R.M. Sutherland, Cancer 58, 1668 (1986)
R.M. Sutherland, Science 240, 177 (1988)
Y. Zeng, T.S. Lee, P. Yu, R. Roy, H.T. Low, Biomech Eng-Trans ASME 128, 185 (2006)
Acknowledgement
The authors wish to thank the financial support of the Natural Sciences and Engineering Research Council through a research grant to D. Li.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Movahed, S., Li, D. Numerical studies of continuous nutrient delivery for tumour spheroid culture in a microchannel by electrokinetically-induced pressure-driven flow. Biomed Microdevices 12, 1061–1072 (2010). https://doi.org/10.1007/s10544-010-9460-z
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10544-010-9460-z