Abstract
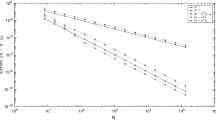
The Il’in scheme is the most famous exponentially fitted finite difference scheme for singularly perturbed boundary value problems. In 1D, Kellogg and Tsan presented a precise error estimate for the scheme from which uniform first order convergence in the discrete maximum norm can be concluded. This estimate is optimal in the sense that one can supply easy examples with smooth data such that the order of uniform convergence of the Il’in scheme is one. In 2D the problem of proving an optimal error estimate remained open. Emel’janov conducted an error analysis giving uniform convergence orders close to one-half. Within the community of singularly perturbed problems it is a legend that this error estimate is sharp. Correcting this mistaken belief it is proven in the present paper that under some conditions the optimal uniform first order convergence of the Il’in scheme in 1D carries over to the two dimensional case. This new result is corroborated by numerical experiments which also shed light on the question in which cases the convergence rate deteriorates.



Similar content being viewed by others
Notes
The upwind operators in both coordinate directions.
References
Allen, D.N., Southwell, R.V.: Relaxation methods applied to determine motion, in two dimensions, of a viscous fluid past a fixed cylinder. J. Mech. Appl. Math. 8, 129–145 (1955)
Andreev, V.B.: Anisotropic estimates for the discrete Green’s function of a monotone difference operator in the singularly perturbed case and its application. Preprint MATHNM-06-2000, Institute für Numerische Mathematik, Technische Universität Dresden, 1–8 (2000)
Andreev, V.B.: Uniform mesh approximation to nonsmooth solutions of a singularly perturbed convection-diffusion equation in a rectangle. Diff. Equ. 45(7), 973–982 (2009)
Andreev, V.B., Savin, I.A.: On the uniform convergence of the monotone Samarski scheme and its modification. J. Vychisl. Mat. i Mat. Fiz. 35, 739–752 (1995)
Emel’janov, K.V.: A difference scheme for a three dimensional elliptic equation with a small parameter multiplying the highest derivative: Boundary value problems for equations of mathematical physics. USSR Academy of Science, Sverdlovsk (1973)
Hegarty, A.F., O’Riordan, E., Stynes, M.: A comparison of uniformly convergent difference schemes for two-dimensional convection-diffusion problems. J. Comput. Phys. 105(1), 24–32 (1993)
Il’in, A.M.: A difference scheme for a differential equation with a small parameter affecting the highest derivative. Mat. Zametki 6, 237–248 (1969). (in Russian)
Kellogg, R.B.: Corner singularities and singular perturbations. Annali dell’Università di Ferrara. Sezione 7: Scienze matematiche 47(1), 177–206 (2001)
Kellogg, R.B., Tsan, A.: Analysis of some difference approximation for a singularly perturbed problem without turning points. Math. Comput. 32, 1025–1039 (1978)
Linß, T., Stynes, M.: Asymptotic analysis and Shishkin-type decomposition for an elliptic convection-diffusion problem. J. Math. Anal. Appl. 261, 604–632 (2001)
Linß, T.: Layer-adapted meshes for reaction-convection-diffusion problems. Lecture Notes in Mathematics. Springer, New York (2010)
Miller, J.J.H., O’Riordan, E., Shishkin, G.I.: Fitted numerical methods for singular perturbation problems, Revised edn. World-Scientific, Singapore (2012)
Morton, K.W.: Numerical Solution of Convection-Diffusion Problems. Chapman & Hall, London (1996)
O’Riordan, E., Stynes, M.: A globally uniformly convergent finite element method for a singularly perturbed elliptic problem in two dimensions. Math. Comput. 57, 47–62 (1991)
Roos, H.-G.: Ten ways to generate the Iljin and related schemes. J. Comput. Appl. Math. 51, 43–59 (1994)
Roos, H.-G., Stynes, M., Tobiska, L.: Robust numerical methods for singularly perturbed differential equations. Springer, New York (2008)
Shishkin, G.I.: Grid approximations of singularly perturbed elliptic and parabolic equations. Ural Branch of Russian Acad. Sci, Ekaterinburg (1992). (in Russian)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Jan Nordström.
Rights and permissions
About this article
Cite this article
Roos, HG., Schopf, M. An optimal a priori error estimate in the maximum norm for the Il’in scheme in 2D. Bit Numer Math 55, 1169–1186 (2015). https://doi.org/10.1007/s10543-014-0536-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10543-014-0536-7