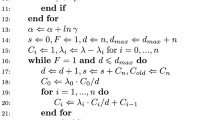Skip to main content

Advertisement

SpringerLink
Log in

A recursive point process model for infectious diseases

  • Published:
Annals of the Institute of Statistical Mathematics Aims and scope Submit manuscript

Abstract

We introduce a new type of point process model to describe the incidence of contagious diseases. The model incorporates the premise that when a disease occurs at low frequency in the population, such as in the primary stages of an outbreak, then anyone with the disease is likely to have a high rate of transmission to others, whereas when the disease is prevalent, the transmission rate is lower due to prevention measures and a relatively high percentage of previous exposure in the population. The model is said to be recursive, in the sense that the conditional intensity at any time depends on the productivity associated with previous points, and this productivity in turn depends on the conditional intensity at those points. Basic properties of the model are derived, estimation and simulation are discussed, and the recursive model is shown to fit well to California Rocky Mountain Spotted Fever data.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  • Akaike, H. (1974). A new look at the statistical model identification. IEEE Transactions on Automatic Control, 19, 716–723.

    Article  MathSciNet  MATH  Google Scholar 

  • Althaus, C. L. (2014). Estimating the reproduction number of Ebola virus (EBOV) during the 2014 outbreak in West Africa. PLOS Current Outbreaks, 6, 1–6.

    Google Scholar 

  • Bacry, E., Delattre, S., Hoffmann, M., Muzy, J. F. (2013). Modeling microstructure noise with mutually exciting point processes. Quantitative Finance, 13, 65–77.

    Article  MathSciNet  MATH  Google Scholar 

  • Bacry, E., Mastromatteo, I., Muzy, J.-F. (2015). Hawkes processes in finance. Market Microstructure and Liquidity, 01(01), 1550005.

    Article  Google Scholar 

  • Balderama, E., Schoenberg, F. P., Murray, E., Rundel, P. W. (2012). Application of branching models in the study of invasive species. Journal of the American Statistical Association, 107(498), 467–476.

    Article  MathSciNet  MATH  Google Scholar 

  • Becker, N. (1977). Estimation for discrete time branching processes with application to epidemics. Biometrics, 33(3), 515–522.

    Article  MathSciNet  MATH  Google Scholar 

  • Cauchemez, S., Nouvellet, P., Cori, A., Jombart, T., Garske, T., Clapham, H., et al. (2016). Unraveling the drivers of MERS-CoV transmission. Proceedings of the National Academy of Sciences, 113(32), 9081–9086.

  • Centers for Disease Control and Prevention. (2015). Chapter 13. In J. Hamborsky, A. Kroger, S. Wolfe (Eds.), Epidemiology and prevention of vaccine-preventable diseases (13th ed., pp. 209–230). Washington D.C.: Public Health Foundation.

  • Chaffee, A. W. (2017). Comparative Analysis of SEIR and Hawkes Models for the 2014 West Africa Ebola Outbreak. MS Thesis, UCLA Statistics, University of California, Los Angeles (pp. 1–32).

  • Clements, R. A., Schoenberg, F. P., Veen, A. (2013). Evaluation of space–time point process models using super-thinning. Environmetrics, 23(7), 606–616.

    Article  MathSciNet  Google Scholar 

  • Daley, D., Vere-Jones, D. (2003). An introduction to the theory of point processes, volume 1: Elementary theory and methods (2nd ed.). New York: Springer.

  • Daley, D., Vere-Jones, D. (2007). An introduction to the theory of point processes, volume 2: General theory and structure (2nd ed.). New York: Springer.

  • Delattre, S., Fournier, N., Hoffmann, M. (2016). Hawkes processes on large networks. Annals of Applied Probability, 26, 216–261.

    Article  MathSciNet  MATH  Google Scholar 

  • Diggle, P. J. (2006). Spatio-temporal point processes, partial likelihood, foot-and-mouth. Statistical Methods in Medical Research, 15, 325–336.

    Article  MathSciNet  MATH  Google Scholar 

  • Diggle, P. J. (2014). Statistical analysis of spatial and spatio-temporal point patterns (3rd ed.). Boca Raton: CRC Press.

  • Farrington, C. P., Kanaan, M. N., Gay, N. J. (2003). Branching process models for surveillance of infectious diseases controlled by mass vaccination. Biostatistics, 4(2), 279–295.

    Article  MATH  Google Scholar 

  • Gordon, J. S., Clements, R. A., Schoenberg, F. P., Schorlemmer, D. (2015). Voronoi residuals and other residual analyses applied to CSEP earthquake forecasts. Spatial Statistics, 14B, 133–150.

    Article  MathSciNet  Google Scholar 

  • Harte, D. S. (2010). PtProcess: An R package for modelling marked point processes indexed by time. Journal of Statistical Software, 35(8), 1–32.

    Article  Google Scholar 

  • Harte, D. S. (2014). An ETAS model with varying productivity rates. Geophysical Journal International, 198(1), 270–284.

    Article  Google Scholar 

  • Harte, D. S. (2015). Log-likelihood of earthquake models: Evaluation of models and forecasts. Geophysical Journal International, 201(2), 711–723.

    Article  Google Scholar 

  • Hawkes, A. G. (1971). Point spectra of some mutually exciting point processes. Journal of the Royal Staistical Society, B33, 438–443.

    MathSciNet  MATH  Google Scholar 

  • Jones, K. E., Patel, N. G., Levy, M. A., Storeygard, A., Balk, D., Gittleman, J. L., et al. (2008). Global trends in emerging infectious diseases. Nature, 451, 990–993.

  • Law, R., Illian, J., Burslem, D. F. R. P., Gratzer, G., Gunatilleke, C. V. S., Gunatilleke, I. A. U. N. (2009). Ecological information from spatial patterns of plants: Insights from point process theory. Journal of Ecology, 97(4), 616–628.

    Article  Google Scholar 

  • Lewis, P. A. W., Shedler, G. S. (1979). Simulation of non-homogeneous Poisson processes by thinning. Naval Research Logistics Quarterly, 26(3), 403–413.

    Article  MathSciNet  MATH  Google Scholar 

  • Lloyd-Smith, J. O., Funk, S., McLean, A. R., Riley, S., Wood, J. L. N. (2015). Nine challenges in modelling the emergence of novel pathogens. Epidemics, 10, 35–39.

    Article  Google Scholar 

  • Meyer, P. (1971). Demonstration simplifiée d’un théorème de Knight. In Séminaire de Probabilités V, Université Strasbourg, Lecture notes in mathematics (Vol. 191, pp. 191–195).

  • Mohler, G. O., Short, M. B., Brantingham, P. J., Schoenberg, F. P., Tita, G. E. (2011). Self-exciting point process modeling of crime. Journal of the American Statistical Association, 106(493), 100–108.

    Article  MathSciNet  MATH  Google Scholar 

  • Ogata, Y. (1978). The asymptotic behavious of maximum likelihood estimators for stationary point processes. Annals of the Institute of Statistical Mathematics, 30, 243–261.

    Article  MathSciNet  MATH  Google Scholar 

  • Ogata, Y. (1988). Statistical models for earthquake occurrence and residual analysis for point processes. Journal of the American Statistical Association, 83, 9–27.

    Article  Google Scholar 

  • Ogata, Y. (1998). Space–time point-process models for earthquake occurrences. Annals of the Institute of Statistical Mathematics, 50(2), 379–402.

    Article  MathSciNet  MATH  Google Scholar 

  • Ogata, Y. (2004). Space–time model for regional seismicity and detection of crustal stress changes. Journal of Geophysical Research, 109(B3), B03308, 1–16.

    Article  Google Scholar 

  • Ogata, Y., Katsura, K., Tanemura, M. (2003). Modelling heterogeneous spacetime occurrences of earthquakes and its residual analysis. Applied Statistics, 52, 499–509.

    MathSciNet  MATH  Google Scholar 

  • Porter, M. D., White, G. (2012). Self-exciting hurdle models for terrorist activity. Annals of Applied Statistics, 6(1), 106–124.

    Article  MathSciNet  MATH  Google Scholar 

  • Schoenberg, F. P. (2006). On non-simple marked point processes. Annals of the Institute of Statistical Mathematics, 58(2), 223–233.

    Article  MathSciNet  MATH  Google Scholar 

  • Schoenberg, F. P. (2013). Facilitated estimation of ETAS. Bulletin of the Seismological Society of America, 103(1), 601–605.

    Article  Google Scholar 

  • Schoenberg, F. P. (2016). A note on the consistent estimation of spatial-temporal point process parameters. Statistica Sinica, 26, 861–789.

    MathSciNet  MATH  Google Scholar 

  • van Panhuis, W. G., Grefenstette, J., Jung, S. Y., Chok, N. S., Cross, A., Eng, H., et al. (2013). Contagious diseases in the United States from 1888 to the present. New England Journal of Medicine, 369(22), 2152–2158.

  • Wallinga, J., Teunis, P. (2004). Different epidemic curves for severe acute respiratory syndrome reveal similar impacts of control measures. American Journal of Epidemiology, 160(6), 509–516.

    Article  Google Scholar 

  • Wang, Q., Schoenberg, F. P., Jackson, D. D., Kagan, Y. Y. (2010). Standard errors of parameter estimates in the ETAS model. Bulletin of the Seismological Society of America, 100(5a), 1989–2001.

    Article  Google Scholar 

  • Zhuang, J. (2015). Weighted likelihood estimators for point processes. Spatial Statistics, 14, 166–178.

    Article  MathSciNet  Google Scholar 

  • Zhuang, J., Ogata, Y., Vere-Jones, D. (2002). Stochastic declustering of space–time earthquake occurrences. Journal of the American Statistical Association, 97(458), 369–380.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This material is based upon work supported by the National Science Foundation under grant number DMS 1513657. Computations were performed in R (https://www.r-project.org). Thanks to the US CDC for supplying the data and to Project Tycho for making it so easily available. Thanks to J. Lloyd-Smith for helpful discussions on disease theory. Thanks to UCLA and Paris for allowing Professor Schoenberg a 1 year sabbatical during which time this research was performed.

Author information

Authors and Affiliations

  1. Department of Statistics, University of California, 8142 Math-Science Building, Los Angeles, CA, 90095–1554, USA

    Frederic Paik Schoenberg

  2. Ceremade, CNRS, PSL Research University, Université Paris-Dauphine, 75016, Paris, France

    Marc Hoffmann

  3. Center for Tropical Research, Institute of the Environment and Sustainability, University of California, Los Angeles, CA, 90095-1554, USA

    Ryan J. Harrigan

Authors
  1. Frederic Paik Schoenberg
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Marc Hoffmann
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ryan J. Harrigan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Frederic Paik Schoenberg.

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Schoenberg, F.P., Hoffmann, M. & Harrigan, R.J. A recursive point process model for infectious diseases. Ann Inst Stat Math 71, 1271–1287 (2019). https://doi.org/10.1007/s10463-018-0690-9

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10463-018-0690-9

Keywords

Search

Navigation