Skip to main content
SpringerLink
Log in

Priors for Bayesian adaptive spline smoothing

  • Published:
Annals of the Institute of Statistical Mathematics Aims and scope Submit manuscript

Abstract

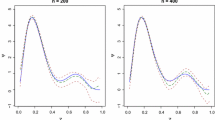
Adaptive smoothing has been proposed for curve-fitting problems where the underlying function is spatially inhomogeneous. Two Bayesian adaptive smoothing models, Bayesian adaptive smoothing splines on a lattice and Bayesian adaptive P-splines, are studied in this paper. Estimation is fully Bayesian and carried out by efficient Gibbs sampling. Choice of prior is critical in any Bayesian non-parametric regression method. We use objective priors on the first level parameters where feasible, specifically independent Jeffreys priors (right Haar priors) on the implied base linear model and error variance, and we derive sufficient conditions on higher level components to ensure that the posterior is proper. Through simulation, we demonstrate that the common practice of approximating improper priors by proper but diffuse priors may lead to invalid inference, and we show how appropriate choices of proper but only weakly informative priors yields satisfactory inference.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Abramovich F., Steinberg D.M. (1996) Improved inference in nonparametric regression using L k -smoothing splines. Journal of Statistical Planning and Inference 49: 327–341

    Article  MathSciNet  MATH  Google Scholar 

  • Abramovich F., Sapatinas T., Silverman B.W. (1998) Wavelet thresholding via a Bayesian approach. Journal of the Royal Statistical Society, Series B: Statistical Methodology 60: 725–749

    Article  MathSciNet  MATH  Google Scholar 

  • Baladandayuthapani V., Mallick B. K., Carroll R.J. (2005) Spatially adaptive Bayesian penalized regression splines (P-splines). Journal of Computational and Graphical Statistics 14: 378–394

    Article  MathSciNet  Google Scholar 

  • Berger J. (2006) The case for objective Bayesian analysis. Bayesian Analysis 1: 385–402

    Article  MathSciNet  Google Scholar 

  • Berger, J. O., Pericchi, L. R. (2001). Objective Bayesian methods for model selection: Introduction and comparison (Pkg: P135-207). In Model selection. Institute of mathematical statistics lecture notes-monograph series (Vol. 38, pp. 135–193). Fountain Hills, AZ: IMS Press.

  • Besag J., Kooperberg C. (1995) On conditional and intrinsic autoregressions. Biometrika 82: 733–746

    MathSciNet  MATH  Google Scholar 

  • Besag J., Green P., Higdon D., Mengersen K. (1995) Bayesian computation and stochastic systems (Disc: P41-66). Statistical Science 10: 3–41

    Article  MathSciNet  MATH  Google Scholar 

  • Brezger A., Fahrmeir L., Hennerfeind A. (2007) Adaptive Gaussian Markov random fields with applications in human brain mapping. Journal of the Royal Statistical Society: Series C (Applied Statistics) 56: 327–345

    Article  MathSciNet  Google Scholar 

  • Carter C.K., Kohn R. (1996) Markov chain Monte Carlo in conditionally Gaussian state space models. Biometrika 83: 589–601

    Article  MathSciNet  MATH  Google Scholar 

  • Chipman H.A., Kolaczyk E.D., McCulloch R.E. (1997) Adaptive Bayesian wavelet shrinkage. Journal of the American Statistical Association 92: 1413–1421

    Article  MATH  Google Scholar 

  • Christensen R. (2002) Plane answers to complex questions: The theory of linear models. Springer, New York

    MATH  Google Scholar 

  • Clyde M., Parmigiani G., Vidakovic B. (1998) Multiple shrinkage and subset selection in wavelets. Biometrika 85: 391–401

    Article  MathSciNet  MATH  Google Scholar 

  • Crainiceanu C., Ruppert D., Carroll R., Adarsh J., Goodner B. (2007) Spatially adaptive penalized splines with heteroscedastic errors. Journal of Computational and Graphical Statistics 16: 265–288

    Article  MathSciNet  Google Scholar 

  • Cummins D.J., Filloon T.G., Nychka D. (2001) Confidence intervals for nonparametric curve estimates: Toward more uniform pointwise coverage. Journal of the American Statistical Association 96: 233–246

    Article  MathSciNet  MATH  Google Scholar 

  • Dass S.C., Berger J.O. (2003) Unified conditional frequentist and Bayesian testing of composite hypotheses. Scandinavian Journal of Statistics 30: 193–210

    Article  MathSciNet  MATH  Google Scholar 

  • Denison D.G.T., Mallick B.K., Smith A.F.M. (1998) Automatic Bayesian curve fitting. Journal of the Royal Statistical Society, Series B 60: 333–350

    Article  MathSciNet  MATH  Google Scholar 

  • Di Matteo I., Genovese C.R., Kass R.E. (2001) Bayesian curve-fitting with free-knot splines. Biometrika 88: 1055–1071

    Article  MathSciNet  Google Scholar 

  • Eilers P., Marx B. (1996) Flexible smoothing with B-splines and penalties (with discussion). Statistical Science 11: 89–121

    Article  MathSciNet  MATH  Google Scholar 

  • Eubank R.L. (1999) Nonparametric regression and spline smoothing. Marcel Dekker, New York

    MATH  Google Scholar 

  • Fahrmeir L., Wagenpfeil S. (1996) Smoothing hazard functions and time-varying effects in discrete duration and competing risks models. Journal of the American Statistical Association 91: 1584–1594

    Article  MathSciNet  MATH  Google Scholar 

  • Friedman J.H. (1991) Multivariate adaptive regression splines (with discussion). The Annals of Statistics 19: 1–141

    Article  MathSciNet  MATH  Google Scholar 

  • Gilks W.R., Wild P. (1992) Adaptive rejection sampling for gibbs sampling. Applied Statistics 41: 337–348

    Article  MATH  Google Scholar 

  • Gilks W.R., Best N.G., Tan K.K.C. (1995) Adaptive rejection Metropolis sampling within gibbs sampling. Applied Statistics 44: 455–472

    Article  MATH  Google Scholar 

  • Green P.J., Silverman B.W. (1994) Nonparametric regression and generalized linear models: A roughness penalty approach. Chapman & Hall, London

    MATH  Google Scholar 

  • Hastie T., Tibshirani R. (2000) Bayesian backfitting (with comments and a rejoinder by the authors). Statistical Science 15: 196–223

    Article  MathSciNet  MATH  Google Scholar 

  • Hastie T., Tibshirani R., Friedman J.H. (2001) The elements of statistical learning: Data mining, inference, and prediction. Springer, Berlin

    MATH  Google Scholar 

  • Hobert J.P., Casella G. (1996) The effect of improper priors on Gibbs sampling in hierarchical linear mixed models. Journal of the American Statistical Association 91: 1461–1473

    Article  MathSciNet  MATH  Google Scholar 

  • Jacquier E., Polson N.G., Rossi P.E. (1994) Bayesian analysis of stochastic volatility models (Disc: P389-417). Journal of Business & Economic Statistics 12: 371–389

    Article  Google Scholar 

  • Johnstone I.M., Silverman B.W. (2005) Empirical Bayes selection of wavelet thresholds. The Annals of Statistics 33: 1700–1752

    Article  MathSciNet  MATH  Google Scholar 

  • Knorr-Held, L. (2003). Some remarks on Gaussian Markov random field models for disease mapping. In N. H. P. Green, S. Richardson (Eds.), Highly structured stochastic systems (pp. 260–264). New York: Oxford University Press.

  • Knorr-Held, L., Richardson, S. (2003). A hierarchical model for space-time surveillance data on meningococcal disease incidence. Journal of the Royal Statistical Society, Series C: Applied Statistics, 52, 169–183.

    Google Scholar 

  • Lang S., Brezger A. (2004) Bayesian P-splines. Journal of Computational and Graphical Statistics 13: 183–212

    Article  MathSciNet  Google Scholar 

  • Lang S., Fronk E.-M., Fahrmeir L. (2002) Function estimation with locally adaptive dynamic models. Computational Statistics 17: 479–499

    Article  MathSciNet  MATH  Google Scholar 

  • Liang, F., Paulo, R., Molina, G., Clyde, M. A., Berger, J. O. (2008). Mixtures of g-priors for Bayesian variable selection. Journal of the American Statistical Association, 103, 410–423.

    Google Scholar 

  • Lindgren F., Rue H. (2008) On the second-order random walk model for irregular locations. Scandinavian Journal of Statistics 35: 691–700

    Article  MathSciNet  MATH  Google Scholar 

  • Mackay D.J.C., Takeuchi R. (1998) Interpolation models with multiple hyperparameters. Statistics and Computing 8: 15–23

    Article  Google Scholar 

  • Marin, J.-M., Robert, C. P. (2007). Bayesian core: A practical approach to computational Bayesian statistics. New York: Springer.

  • Nakatsuma, T. (2000). Bayesian analysis of ARMA-GARCH models: A Markov chain sampling approach. Journal of Econometrics, 95, 57–69.

    Google Scholar 

  • Ngo L., Wand M. (2004) Smoothing with mixed model software. Journal of Statistical Software 9: 1–54

    Google Scholar 

  • Paciorek, C. J., Schervish, M. J. (2004). Nonstationary covariance functions for Gaussian process regression. In S. Thrun, L. Saul, B. Schölkopf (Eds.), Advances in neural information processing systems (Vol. 16). Cambridge, MA: MIT Press.

  • Paciorek C.J., Schervish M.J. (2006) Spatial modelling using a new class of nonstationary covariance functions. Environmetrics 17: 483–506

    Article  MathSciNet  Google Scholar 

  • Pensky M. (2006) Frequentist optimality of Bayesian wavelet shrinkage rules for Gaussian and non-Gaussian noise. The Annals of Statistics 34: 769–807

    Article  MathSciNet  MATH  Google Scholar 

  • Pintore A., Speckman P.L., Holmes C.C. (2006) Spatially adaptive smoothing splines. Biometrika 93: 113–125

    Article  MathSciNet  MATH  Google Scholar 

  • Rue, H., Held, L. (2005). Gaussian Markov random fields: Theory and applications. Monographs on statistics and applied probability (Vol. 104). London: Chapman & Hall.

  • Ruppert, D., Carroll, R. J. (2000). Spatially-adaptive penalties for spline fitting. Australian & New Zealand Journal of Statistics, 42, 205–223.

    Google Scholar 

  • Ruppert, D., Wand, M., Carroll, R. (2003). Semiparametric regression. Cambridge: Cambridge University Press.

  • Smith M.S., Kohn R.J. (1996) Nonparametric regression using bayesian variable selection. Journal of Econometrics 75: 317–343

    Article  MATH  Google Scholar 

  • Speckman P.L., Sun D. (2003) Fully Bayesian spline smoothing and intrinsic autoregressive priors. Biometrika 90: 289–302

    Article  MathSciNet  MATH  Google Scholar 

  • Staniswalis J.G. (1989) Local bandwidth selection for kernel estimates. Journal of the American Statistical Association 84: 284–288

    Article  MathSciNet  MATH  Google Scholar 

  • Staniswalis J.G., Yandell B.S. (1992) Locally adaptive smoothing splines. Journal of Statistical Computation and Simulation 43: 45–53

    Article  MathSciNet  Google Scholar 

  • Sun, D., Speckman, P. L. (2008). Bayesian hierarchical linear mixed models for additive smoothing splines. Annals of the Institute of Statistical Mathematics, 60, 499–517.

    Google Scholar 

  • Sun, D., Tsutakawa, R. K., He, Z. (2001). Propriety of posteriors with improper priors in hierarchical linear mixed models. Statistica Sinica, 11, 77–95.

    Google Scholar 

  • Sun D., Tsutakawa R.K., Speckman P.L. (1999) Posterior distribution of hierarchical models using CAR(1) distributions. Biometrika 86: 341–350

    Article  MathSciNet  MATH  Google Scholar 

  • Van Der Linde A. (2003) PCA-based dimension reduction for splines. Journal of Nonparmetric Statistics 15: 77–92

    Article  MathSciNet  MATH  Google Scholar 

  • Vrontos, I. D., Dellaportas, P., Politis, D. N. (2000). Full Bayesian inference for GARCH and EGARCH models. Journal of Business & Economic Statistics, 18, 187–198.

    Google Scholar 

  • Wahba, G. (1990). Spline models for observational data. Philadelphia: SIAM.

  • Wand M. (2000) A comparison of regression spline smoothing procedures. Computational Statistics 15: 443–462

    Article  MathSciNet  MATH  Google Scholar 

  • Wand M., Jones M. (1995) Kernel smoothing. Chapman & Hall, London

    MATH  Google Scholar 

  • White, G. (2006). Bayesian semi-parametric spatial and joint spatio-temporal smoothing. Ph.D. thesis, University of Missouri-Columbia, Columbia, MO.

  • Wood S., Jiang W., Tanner M. (2002) Bayesian mixture of splines for spatially adaptive nonparametric regression. Biometrika 89: 513–528

    Article  MathSciNet  MATH  Google Scholar 

  • Yue Y., Speckman P.L. (2010) Nonstationary spatial Gaussian Markov random fields. Journal of Computational and Graphical Statistics 19: 96–116

    Article  MathSciNet  Google Scholar 

  • Zellner, A. (1986). On assessing prior distributions and Bayesian regression analysis with g-prior distributions. In P. K. Goel, A. Zellner (Eds.), Bayesian inference and decision techniques: Essays in honor of Bruno de Finetti (pp. 233–243). New York/Amsterdam: Elsevier/North-Holland.

  • Zellner, A., Siow, A. (1980). Posterior odds ratios for selected regression hypotheses. In J. M. Bernardo, M. H. DeGroot, D. V. Lindley, A. F. M. Smith (Eds.), Bayesian statistics: Proceedings of the first international meeting held in Valencia (Spain) (pp. 585–603). Valencia: University of Valencia.

Download references

Author information

Authors and Affiliations

  1. Department of Statistics and CIS, Baruch College, City University of New York, One Bernard Baruch Way, New York, NY, 10010, USA

    Yu Ryan Yue

  2. Department of Statistics, University of Missouri, 146 Middlebush Hall, Columbia, MO, 65211, USA

    Paul L. Speckman & Dongchu Sun

Authors
  1. Yu Ryan Yue
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Paul L. Speckman
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Dongchu Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yu Ryan Yue.

Additional information

Supported by PSC-CUNY Grant 60147-39 40 and National Science Foundation Grant 0720229.

About this article

Cite this article

Yue, Y.R., Speckman, P.L. & Sun, D. Priors for Bayesian adaptive spline smoothing. Ann Inst Stat Math 64, 577–613 (2012). https://doi.org/10.1007/s10463-010-0321-6

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10463-010-0321-6

Keywords

Search

Navigation