Graph cuts with interacting edge weights: examples, approximations, and algorithms

Abstract

We study an extension of the classical graph cut problem, wherein we replace the modular (sum of edge weights) cost function by a submodular set function defined over graph edges. Special cases of this problem have appeared in different applications in signal processing, machine learning, and computer vision. In this paper, we connect these applications via the generic formulation of “cooperative graph cuts”, for which we study complexity, algorithms, and connections to polymatroidal network flows. Finally, we compare the proposed algorithms empirically.

Appendices

Appendix: Cooperative multi-cut and sparsest cut

An extension of MinCoopCut is the problem of cooperative multi-way cut and sparsest cut. Using the approximation $\hat{f}_{ea}$ from Sect. 5.1.3, we can transform any multi-way or sparsest cut problem with a submodular cost function on edges (instead of a sum of edge weights) into a cut problem whose cut cost is a convolution of local submodular functions. The relaxation of this cut problem is dual to the polymatroidal flow problems considered by Chekuri et al. [13]. Combining their results with ours, we get the following Lemma.

Lemma 11

Let $\alpha$ be the approximation factor for solving a sparsest cut / multi-way cut in a polymatroidal network. If we solve a cooperative sparsest cut / multi-way cut by first approximating the cut cost f by a function $\hat{f}_{ea}$ and, on this instance, using the method with factor $\alpha$, we get an $O(\alpha n)$-approximation for cooperative sparsest cut / multi-way cut.

Using Theorems 6 and 8 in Chekuri et al. [13], we obtain the following bounds:

Corollary 2

There is an $O(n\log k)$ approximation for cooperative sparsest cut in undirected graphs that is dual to a maximum multicommodity flow problem with k pairs, and an $O(n\log k)$ approximation for cooperative multi-way cut.

We leave it as an open problem whether these bounds are optimal.

Proof of proposition 2

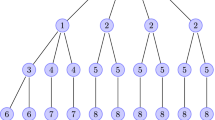
The first part of Proposition 2 is proven by Fig. 1. Here, we show the second part that the function $h(X) = f(\delta ^+(X))$ is subadditive if f is nondecreasing and submodular. Let $X,Y \subseteq \mathcal {V}$. Then it holds that

$$\begin{aligned} h(X) + h(Y)&= f( \delta ^+(X)) + f(\delta ^+(Y)) \end{aligned}$$

(45)

$$\begin{aligned}&\ge f( \delta ^+(X) \cup \delta ^+(Y)) + f( \delta ^+(X) \cap \delta ^+(Y)) \end{aligned}$$

(46)

$$\begin{aligned}&\ge f( \delta ^+(X) \cup \delta ^+(Y)) \end{aligned}$$

(47)

$$\begin{aligned}&\ge f( \delta ^+(X \cup Y)) \end{aligned}$$

(48)

$$\begin{aligned}&= h(X \cup Y). \end{aligned}$$

(49)

In Inequality (46), we used that f is submodular, and in Inequality (47), we used that f is nonnegative.

Reduction from Graph Bisection to MinCoopCut

In this section, we prove Theorem 2 via a reduction from Graph Bisection, which is known to be NP-hard [21].

Definition 2

(Graph Bisection) Given a graph $\mathcal {G}_B = (\mathcal {V}_B,\mathcal {E}_B)$ with edge weights $w_B: \mathcal {E}_B \rightarrow {\mathbb {R}}_+$, find a partition $V_1 \dot{\cup }V_2 = \mathcal {V}_B$ with $|V_1| = |V_2| = |\mathcal {V}_B|/2$ with minimum cut weight $w(\delta (V_1))$.

Proof

To reduce Graph Bisection to MinCoopCut, we construct an auxiliary graph $\mathcal {G}= (\mathcal {V}_B \cup \{s,t\}, \mathcal {E}_B \cup \mathcal {E}_s \cup \mathcal {E}_t)$ that contains an unchanged copy of $\mathcal {G}_B$ and two additional terminal nodes s, t. The submodular weights on the edges adjacent to the terminal nodes will express the balance constraint $|V_1| = |V_2| = |\mathcal {V}_B|/2$. In $\mathcal {G}$, we retain the modular costs w on $\mathcal {E}_B$ and connect s, t to every vertex in $\mathcal {G}_B$ with corresponding new edge sets $\mathcal {E}_s$ and $\mathcal {E}_t$, as illustrated in Fig. 7a. The cost of a cut in $\mathcal {G}$ is measured by the submodular function

$$\begin{aligned} f(C) = \sum _{e \in C \cap \mathcal {E}_B}w(e) + \beta f_{bal}(C \cap (\mathcal {E}_s \cup \mathcal {E}_t)), \end{aligned}$$

(50)

where $\beta$ is an appropriately large constant, and $f_{bal}$ will be defined later. Obviously, any minimal (s, t)-cut C must include $n_B=|\mathcal {V}_B|$ edges from $\mathcal {E}_s \cup \mathcal {E}_t$, and partitions $\mathcal {V}_B$. Moreover, the cardinality of $C_s = C \cap \mathcal {E}_s$ is the number of nodes in $\mathcal {V}_B$ assigned to t. Hence, in an equipartition, $|C_s| = |C_t| = n_B/2$, where $C_t = C \cap \mathcal {E}_t$.

Fig. 7

Graph for the reduction and examples for the definition of $f_{bal}$ via ranks $h_\sigma$, with $n_B=6$. In (c), $C_s=\{(s,v_1), (s,v_2)\}$ and $C_t=\{(v_3,t), (v_4,t), (v_5,t),(v_6,t)\}$; in (d), $C_s=\{(s,v_1), (s,v_4),(s,v_5)\}$ and $C_t=\{(v_2,t), (v_3,t),(v_6,t)\}$. Connected components are indicated by dashed lines. a graph $\mathcal {G}$ with $\mathcal {E}_s$ (blue), $\mathcal {E}_t$ (red) and $\mathcal {G}_B$ (black). b graph $\mathcal {H}_\sigma$. c $h_\sigma (\phi (C))=5$ connected components. d Balanced cut C: $h_\sigma (\phi (C))=3$ connected components (color figure online)

It remains to define $f_{bal}$ as a nondecreasing submodular function that implements the equipartition constraint. The function will be an expectation over matroid rank functions $h_\sigma$. Let $\mathcal {H}_\sigma = (\mathcal {E}_s, \mathcal {E}_t, \mathcal {F}_{\sigma })$ be a bipartite graph with nodes $\mathcal {E}_s \cup \mathcal {E}_t$ whose edges $\mathcal {F}_{\sigma }$ form a derangement between $\mathcal {E}_s$ and $\mathcal {E}_t$, as illustrated in Fig. 7b.

Let $\phi (C_s \cup C_t)$ be the image of $C_s \cup C_t$ in the set of nodes of $\mathcal {H}_\sigma$. The function $h_{\sigma }: 2^{\phi (\mathcal {E}_s \cup \mathcal {E}_t)} \rightarrow {\mathbb {N}}_0$ counts the number of connected components in the subgraph induced by the nodes $\phi (C_s \cup C_t)$, and is the rank of a partition matroid. Figure 7 shows some examples.

Let ${\mathfrak {S}}$ be the set of all derangements $\sigma$ of $n_B$ elements, i.e., all possible edge configurations in $\mathcal {H}_\sigma$. We define $f_{bal}$ to be the expectation (under uniform draws of $\sigma$)

$$\begin{aligned} f_{bal}(C) = {\mathbb {E}}_\sigma [h_\sigma (\phi (C))] = |{\mathfrak {S}}|^{-1}\sum \nolimits _{\sigma \in {\mathfrak {S}}} h_\sigma (\phi (C)). \end{aligned}$$

(51)

For a fixed derangement $\sigma '$ and a fixed size $|C_s \cup C_t|=n_B$, the value $h_{\sigma '}(C_s \cup C_t)$ is minimal if $\sigma '(C_s) = C_t$ and $|C_s| = |C_t|$. For a fixed $\sigma$, the rank $h_{\sigma }(C)$ is $|\phi (C_s \cup C_t)| = |C_s|+|C_t|$ minus the matching nodes. Denoting $(s,v_i)$ in $\mathcal {H}_{\sigma }$ by $x_i$ and $(v_i,t)$ by $y_i$, the rank is

$$\begin{aligned} h_{\sigma }(\phi (C_s) \cup \phi (C_t))&= |C_s| + |C_t| - {\Big | \big \{ (x_i, y_{\sigma (i)}) \big \}_{i=1}^n\; \cap \; (\phi (C_s) \times \phi (C_t)) \Big |}. \end{aligned}$$

(52)

Hence, the sum in (51) becomes

$$\begin{aligned} \sum _{\sigma \in {\mathfrak {S}}} h_\sigma (C)&= |{\mathfrak {S}}|\big (|C_s| + |C_t|\big ) -\sum _{\sigma \in {\mathfrak {S}}} \big | \big \{ (x_i, y_{\sigma (i)}) \big \}_{i=1}^n\, \cap \, (\phi (C_s) \times \phi (C_t)) \big | \end{aligned}$$

(53)

$$\begin{aligned}&= |{\mathfrak {S}}|\big (|C_s| + |C_t|\big ) - \sum _{x_i \in \phi (C_s)} \sum _{\sigma \in {\mathfrak {S}}} \big | (x_i, y_{\sigma (i)}) \cap (\{x_i\} \times \phi (C_t)) \big | \end{aligned}$$

(54)

To compute the sum over $\sigma$ in the second term, let $C_{s\cap t} \triangleq \{ (s, v)\, |\, \{(s,v),(v, t)\} \subseteq C\}$ be the set of s-edges whose counterpart on the t side is also contained in C. Let further $D'(n_B-1)$ denote the number of permutations of $n_B-1$ elements (pair $(x_i,y_k)$, i.e., $\sigma (i)=k$, is fixed), where one specific element $x_k$ can be mapped to any other of the $n_B-1$ elements, and the remaining elements must not be mapped to their counterparts ($\sigma (j) \ne j$). Then there are $D'(n_B-1)$ derangements $\sigma$ realizing a specific mapping $\sigma (i)=k$. Denoting the number of derangements of n elements by D(n), the sum above becomes

$$\begin{aligned} D(n_B) f_{bal}(C)&= (|C_s| + |C_t|)D(n_B) \nonumber \\&\quad \quad - \sum _{x_i \in C_s {\setminus } C_{s \cap t}} \sum _{y_k \in C_t} D'(n_B-1) - \sum _{x_i \in C_{s \cap t}} \sum _{y_k \in C_t, k\ne i} D'(n_B-1) \end{aligned}$$

(55)

$$\begin{aligned}&= (|C_s| + |C_t|)D(n_B)\nonumber \\&\quad \quad - \big (|C_s| - |C_{s \cap t}|\big )|C_t|D'(n_B-1) - |C_{s \cap t}| (|C_t|-1) D'(n_B-1) \end{aligned}$$

(56)

$$\begin{aligned}&= (|C_s| + |C_t|)D(n_B) - (|C_s||C_t| - |C_{s \cap t}|) D'(n_B-1), \end{aligned}$$

(57)

with $D(n) = |{\mathfrak {S}}| = n! \sum _{k=0}^n (-1)^k / k!$ [67], and $D'(n-1) = \sum _{k=0}^{n-1} (n-2)!(n-1-k)!(-1)^k$ by Proposition 4 below.

Given that $|C_s| + |C_t|$ must cut at least $n_B$ edges and that $f_{bal}$ is increasing, $f_{bal}$ is minimized if $|C_s| = |C_t| = n_B/2$. As a result, if $\beta$ is large enough such that $f_{bal}$ dominates the cost, then a minimum cooperative cut in $\mathcal {G}$ bisects the $\mathcal {G}_B$ subgraph of $\mathcal {G}$ optimally. $\square$

Proposition 4

Let $D'(n)$ be the number of permutations of n elements where for one fixed element $i'$ we allow $\sigma (i') \in \{1, \ldots , n\}$, but $\sigma (i) \ne i$ for all $i \ne i'$. Then $D'(n) = \sum _{k=0}^{n} \frac{(n-1)!}{k!}(n-k)! (-1)^k$.

Proof

$D'(n)$ can be derived by the method of the forbidden board [67, pp. 71-73]. Let, without loss of generality, $i'=n$, so the forbidden board is $B = \{(1,1), (2,2), \ldots , (n-1,n-1)\}$. Let $N_j$ be the number of permutations $\sigma$ for which $\big |\{(i,\sigma (i)\}_{i=1}^n \cap B\big | = j$, and let $r_k$ be the number of k-subsets of B such that no two elements have a coordinate in common. Here, $r_k~=~{n-1 \atopwithdelims ()k}$. Then $D'(n) = N_0 = N_n(0)$ for

$$\begin{aligned} N_n(x)&= \sum _j N_j x^j = \sum _{k=0}^n r_k (n-k)!(x-1)^k = \sum _{k=0}^{n} \frac{(n-1)!}{k!} (n-k) (x-1)^k, \end{aligned}$$

(58)

and hence $D'(n) = \sum _{k=0}^{n} \frac{(n-1)!}{k!} (n-k)! (-1)^k$ (Fig. 8). $\square$

Convolutions of submodular functions are not always submodular

The non-submodularity of convolutions was mentioned already in Lovász [54]. For completeness, we show an explicit example that illustrates that non-submodularity also holds for the special case of polymatroidal flows.

Proposition 5

The convolution of two submodular functions $(f *g)(A) = \min _{B \subseteq A}f(B) + g(A{\setminus } B)$ is not in general submodular. In particular, this also holds for the cut cost functions occurring in the dual problems of polymatroidal maximum flows.

Fig. 8

Example showing that the convolution of submodular functions is not always submodular, e.g., for $a = 1.5$, $b=2$ and $\epsilon = 0.001$

To show Proposition 5, consider the graph in Fig. 5 with a submodular edge cost function $f(A) = \max _{e \in A}w(e)$. The two submodular functions that are convolved in the corresponding polymatroidal flow are the decompositions

$$\begin{aligned} {\mathrm {cap}}^{\text {out}}(A)&= \sum _{v \in \mathcal {V}} f(A \cap \delta ^+(v)) \end{aligned}$$

(59)

$$\begin{aligned} {\mathrm {cap}}^{\text {in}}(A)&= \sum _{v \in \mathcal {V}} f(A \cap \delta ^-(v)). \end{aligned}$$

(60)

Both ${\mathrm {cap}}^{\text {out}}$ and ${\mathrm {cap}}^{\text {in}}$ are submodular functions from $2^\mathcal {E}$ to ${\mathbb {R}}_+$. Their convolution h is

$$\begin{aligned} h(A) = ({\mathrm {cap}}^{\text {out}} *{\mathrm {cap}}^{\text {in}})(A) = \min _{B \subseteq A}{\mathrm {cap}}^{\text {out}}(B) + {\mathrm {cap}}^{\text {in}}(A {\setminus } B) = \hat{f}_{pf}(A). \end{aligned}$$

(61)

For h to be submodular, it must satisfy the condition of diminishing marginal costs, i.e., for any e and $A \subseteq B \subseteq \mathcal {E}{\setminus } e$, it must hold that $h(e \mid A) \ge h(e \mid B)$. Now, let $A = \{e_2\}$ and $B = \{e_1, e_2\}$. The convolution here means to pair $e_3$ either with $e_1$ or $e_2$. Then, if $a < b$,

$$\begin{aligned} h(e_3 \mid A)&= \min \{a+b, b\} - a = b-a \end{aligned}$$

(62)

$$\begin{aligned} h(e_3 \mid B)&= a + b - \min \{a+a,a\} = b. \end{aligned}$$

(63)

Hence, $h(e_3 \mid A) < h(e_3 \mid B)$, disproving submodularity of h.

Cooperative cuts and polymatroidal networks

We next prove Lemma 6 that relates the approximation $\hat{f}_{pf}$ to maxflow problems in polymatroidal networks.

Proof

(Lemma 6 ) The first step is the dual of the polymatroidal flow. Let ${\mathrm {cap}}^{\text {in}}: 2^\mathcal {E}\rightarrow {\mathbb {R}}_+$ be the joint incoming capacity, ${\mathrm {cap}}^{\text {in}}(C) = \sum _{v \in V}{\mathrm {cap}}_v^{\text {in}}(C \cap \delta ^-v)$, and let equivalently ${\mathrm {cap}}^{\text {out}}$ be the joint outgoing capacity. The dual of the polymatroidal maximum flow is a minimum cut problem whose cost is a convolution of edge capacities [54]:

$$\begin{aligned} {\mathrm {cap}}(C) = ({\mathrm {cap}}^{\text {in}} *{\mathrm {cap}}^{\text {out}})(C) \;\triangleq \; \min _{A \subseteq C} \bigl [ {\mathrm {cap}}^{\text {in}}(A) + {\mathrm {cap}}^{\text {out}}(C {\setminus } A) \bigr ]. \end{aligned}$$

(64)

We will relate this dual to the approximation $\hat{f}_{pf}$. Given a minimal (s, t)-cut C, let $\varPi (C)$ be a partition of C, and $C_v^{\text {in}} = C^\varPi _v \cap \delta ^-_v$ and $C_v^{\text {out}} = C^\varPi _v \cap \delta ^+_v$. The cut C partitions the nodes into two sets $\mathcal {V}_s$ containing s and $\mathcal {V}_t$ containing t. Since C is a minimal directed cut, it contains only edges from the s side $\mathcal {V}_s$ to the t side $\mathcal {V}_t$ of the graph. In consequence, $C_v^{\text {in}} = \emptyset$ if v is on the s side, and $C_v^{\text {out}} = \emptyset$ otherwise. Hence, $C^{\text {in}}_v \cup C^{\text {out}}_v$ is equal to either $C^{\text {in}}_v$ or $C^{\text {out}}_v$, and since $f(\emptyset )=0$, it holds that $f(C^{\text {in}}_v \cup C^{\text {out}}_v) = f(C^{\text {in}}_v) + f(C^{\text {out}}_v)$. Then, starting with the definition of $\hat{f}_{pf}$,

$$\begin{aligned} \hat{f}_{pf}(C)&= \min _{\varPi (C) \in {\mathcal {P}}_C}\sum \nolimits _{v \in \mathcal {V}}f(C^{\varPi }_v) \end{aligned}$$

(65)

$$\begin{aligned}&= \min _{\varPi (C) \in {\mathcal {P}}_C} \sum \nolimits _{v \in \mathcal {V}}f(C^{\text {in}}_v \cup C^{\text {out}}_v) \end{aligned}$$

(66)

$$\begin{aligned}&= \min _{\varPi (C) \in {\mathcal {P}}_C} \sum \nolimits _{v \in \mathcal {V}}\bigl [f(C^{\text {in}}_v) + f(C^{\text {out}}_v)\bigr ] \end{aligned}$$

(67)

$$\begin{aligned}&= \min _{\varPi (C) \in {\mathcal {P}}_C} \sum \nolimits _{v \in \mathcal {V}}\bigl [{\mathrm {cap}}_v^{\text {in}}(C^{\text {in}}_v) + {\mathrm {cap}}_v^{\text {out}}(C^{\text {out}}_v)\bigr ] \end{aligned}$$

(68)

$$\begin{aligned}&= \min _{C^{\text {in}},C^{\text {out}}} \bigl [{\mathrm {cap}}^{\text {in}}(C^{\text {in}}) + {\mathrm {cap}}^{\text {out}}(C^{\text {out}})\bigr ] \end{aligned}$$

(69)

$$\begin{aligned}&= \min _{C^{\text {in}} \subseteq C} \bigl [{\mathrm {cap}}^{\text {in}}(C^{\text {in}}) + {\mathrm {cap}}^{\text {out}}(C {\setminus } C^{\text {in}})\bigr ] \end{aligned}$$

(70)

$$\begin{aligned}&= ({\mathrm {cap}}^{\text {in}} *{\mathrm {cap}}^{\text {out}})(C). \end{aligned}$$

(71)

The minimum in Eq. (67) is taken over all feasible partitions $\varPi (C)$ and their resulting intersections with the sets $\delta ^+v, \delta ^-v$. Then we use the notation $C^{\text {in}} = \bigcup _{v \in \mathcal {V}}C_v^{\text {in}}$ for all edges assigned to their head nodes, and $C^{\text {out}} = \bigcup _{v \in \mathcal {V}}C_v^{\text {out}}$. The minima in Eqs. (69) and (70) are again taken over all partitions in ${\mathcal {P}}_C$. The final equality follows from the above definition of a convolution of submodular functions. $\square$