Expectation-maximization algorithms for inference in Dirichlet processes mixture

Abstract

Mixture models are ubiquitous in applied science. In many real-world applications, the number of mixture components needs to be estimated from the data. A popular approach consists of using information criteria to perform model selection. Another approach which has become very popular over the past few years consists of using Dirichlet processes mixture (DPM) models. Both approaches are computationally intensive. The use of information criteria requires computing the maximum likelihood parameter estimates for each candidate model whereas DPM are usually trained using Markov chain Monte Carlo (MCMC) or variational Bayes (VB) methods. We propose here original batch and recursive expectation-maximization algorithms to estimate the parameters of DPM. The performance of our algorithms is demonstrated on several applications including image segmentation and image classification tasks. Our algorithms are computationally much more efficient than MCMC and VB and outperform VB on an example.

1 Introduction

Finite mixture models are used in numerous applications for density estimation and model-based clustering [14]. In many cases, the number of components of the mixture is unknown and needs to be estimated from the data. Two popular approaches have been developed to address this problem in the literature.

The standard approach consists of performing model selection using an information criterion such as Akaike information criterion or Bayesian information criterion. This requires computing the maximum likelihood estimates of the parameters for each model candidate. This is typically performed using the celebrated expectation-maximization (EM) algorithm [7] which allows us to find easily local maxima of the likelihood function. However, if the number of model candidates is large, then this approach is expensive.

Over the past few years, an alternative approach has become very popular in machine learning and pattern recognition. It relies on the class of Dirichlet process mixture (DPM) models. In this approach, a prior on the number of components of the mixture is implicitly introduced through the so-called stick-breaking construction [4, 10]. DPM models have attractive properties but are unfortunately difficult to learn and inference is typically carried out using VB [4] or Markov chain Monte Carlo (MCMC) methods [10]. Both approaches are very computationally intensive.

The main contributions of our paper is to present here original batch and recursive EM algorithms for parameter estimation in DPMs which allows us to do jointly parameter and model selection. We additionally propose an original method to select automatically the scale parameter of the DPM model which has a crucial influence on the inference results.

Batch EM algorithms need to compute an expectation w.r.t the whole data set before updating the parameters and can be quite computationally intensive for large data sets. Our batch EM algorithm for DPM is no exception. To mitigate this problem, recursive EM ideas have appeared over the past few years where we compute an expectation w.r.t a single data point before updating the parameters [12, 17, 18, 20]. The algorithms discussed in these references have enjoyed some successes but suffer from several drawbacks. In particular, if the parameters we are interested in are constrained to a manifold—e.g., the simplex or the space of positive definite matrices—then the update rules described in earlier work rely on some complex reprojection steps. The recursive EM algorithm for DPMs proposed here follows the alternative approach initiated in [1, 16] for standard finite mixture of Gaussians. Such recursive EM approaches have surprisingly not been widely adopted, whereas they do not suffer from the problems encountered by the algorithms presented in [12, 17, 18, 20] and are a direct extension of the batch EM algorithm. We demonstrate these EM algorithms on various datasets and show that they can outperform state-of-the-art variational Bayesian approaches developed for DPM for a fraction of their computational complexity [4]. To be precise, we should mention that our EM algorithms are only applicable to a truncated version of the DPM model where the number of possible components is restricted to a large number. Similar truncation approaches have been adopted in [4, 10].

The rest of this paper is organized as follows: in Sect. 2, we review the class of finite mixture models and the batch and recursive EM algorithm in this framework. In Sect. 3, we present the class of DPM models and present original batch and recursive EM algorithms to fit a truncated version of the DPM models. We demonstrate the performance of our model and algorithms in Sect. 4.

2 Finite mixture models and EM algorithms

2.1 Finite mixture model

Let $y_{1},\ldots,y_{T}\in\mathcal{Y}$ be independent and identically distributed random variables. We model the distribution of the observations using a parametric family of pdfs $\{ g(y\vert \Upphi);\Upphi\in\varvec{\Upphi}\}.$ We assume that $g( y\vert \Upphi)$ is a mixture of k components

$$ g(y\vert \Upphi)=\sum_{i=1}^{k}\pi_{i}f_{i}(y\vert \theta_{i}) $$

where $\Upphi=(\pi_{1},\ldots,\pi_{k},\theta_{1},\ldots,\theta_{k}),f_{i}(y;\theta_{i})$ the probability density function of the ith component, π _i  ≥ 0 and ∑ ^k _i=1 π _i  = 1. Further, we will introduce the missing data $x_{1},\ldots,x_{T}$ where $x_{n}\in\{ 1,\ldots,k\}$ corresponds to the component associated with y _n ; that is, we have

$$ g(y\vert \Upphi)=\sum_{i=1}^{k}f(x=i,y\vert \Upphi) $$

where

$$ f(x,y\vert \Upphi)=\pi_{x}f_{x}( y\vert \theta_{x}). $$

We give here two illustrative examples:

Example 1

Mixture of multivariate Gaussians.

For observations in ${\mathcal{Y}=\mathbb{R}^{d},}$ we have

$$ g(y\vert \Upphi) =\sum_{i=1}^{k}\pi_{i} {\mathcal{N}}( y;m_{i},\Upsigma_{i}) $$

where $\mathcal{N}(z;m,\Upsigma)$ is the multivariate Gaussian density of argument z, mean m and covariance $\Upsigma.$ In this case, we have $\Upphi=\{( \pi_{i},m_{i},\Upsigma_{i});\; i=1,\ldots,k\}$ and

$$ \begin{aligned} \log f(x,y\vert \Upphi) & =\log\pi_{x}-\frac{n} {2}\log(2\pi) -\frac{1}{2}\log \vert \Upsigma_{x} \vert -\frac{1}{2}( y-m_{x}) ^{\rm T}\Upsigma_{x}^{-1}( y-m_{x})\\ & =-\frac{n}{2}\log (2\pi) +\sum_{i=1}^{k}\left( \log\pi _{i}-\frac{1}{2}\log \vert \Upsigma_{i} \vert -\frac{1}{2}y^{\rm T}\Upsigma_{i}^{-1}y-\frac{1}{2}m_{i}^{\rm T}\Upsigma_{i}^{-1}m_{i}-y^{\rm T}\Upsigma_{i}^{-1}m_{i}\right)\cdot\delta_{i}(x) \end{aligned} $$

where δ _i (x) = 1 if x = i and 0 otherwise.

Example 2

Mixture of Poisson distributions.

We have ${\mathcal{Y}=\mathbb{N}}$ and

$$ g(y\vert \Upphi) =\sum_{i=1}^{k}\pi_{i} {\mathcal{P}}(y;\lambda_{i}) $$

where $\mathcal{P}( z;\lambda)$ is the Poisson distribution of argument z and mean λ. In this case we have

$$ \begin{aligned} \log f(x,y\vert \Upphi) & =\log\pi_{x} -y\log(\lambda_{x}) -\log(y!) -\lambda_{x} \\ & =-\log( y!) +\sum_{i=1}^{k}( \log\pi_{i}-y\log( \lambda_{i}) -\lambda_{i})\cdot\delta_{i}(x) \end{aligned} $$

In the rest of the paper, we will limit ourselves to the multivariate Gaussian case but the algorithms presented later on can be applied to any scenario where f _i (y; θ _i ) belongs to the exponential family.

2.2 Batch and recursive EM algorithms for finite mixture models

2.2.1 Batch EM

For any generic sequence {z _t }, we use the notation $z_{i:j}=(z_{i},z_{i+1},\ldots,z_{j}).$ Consider we are interested in maximizing the likelihood of the observations y _1:T . The EM algorithm is an iterative algorithm which proceeds as follows at iteration j:

$$ \Upphi^{(j)}=\underset{\Upphi\in\varvec{\Upphi}}{\arg\max}Q(\Upphi,\Upphi^{(j-1)}) $$

where

$$ Q(\Upphi,\Upphi^{(j-1)})={\mathbb{E}}[ \log f(x_{1:T},y_{1:T}\vert \Upphi)\vert y_{1:T},\Upphi^{(j-1)}].$$

We can also easily modify this EM algorithm to maximize the penalized likelihood associated with a prior distribution $p(\Upphi)$.

Example 1 (continued)

We have

$$ Q(\Upphi,\Upphi^{( j-1) }) =\sum_{t=1}^{T}\sum _{i=1}^{k}\left( \log\pi_{i}-\frac{1}{2}\log\vert \Upsigma_{i}\vert -\frac{1}{2}y_{t}^{\rm T}\Upsigma_{i}^{-1}y_{t}-\frac{1}{2}m_{i}^{\rm T} \Upsigma_{i}^{-1}m_{i}-y_{t}^{\rm T}\Upsigma_{i}^{-1}m_{i}\right) \cdot\Pr(x_{t}=i\vert y_{t},\Upphi^{( j-1) }) $$

where

$$ \Pr (x_{t}=i \vert y_{t},\Upphi^{(j-1) }) =\frac{\pi_{i}^{(j-1)}\cdot{\mathcal{N}}\left( y_{t} ;m_{i}^{(j-1)},\Upsigma_{i}^{( j-1) }\right)} {\sum_{l=1}^{k}\pi_{l}^{(j-1) }\cdot{\mathcal{N}}\left( y_{t} ;m_{l}^{(j-1) },\Upsigma_{l}^{( j-1)}\right)}. $$

In this case, the Q function is maximized for

$$ \pi_{i}^{(j)} =\frac{\sum_{t=1}^{T}{\mathbb{E}}\left[\delta_{i}(x_{t})\vert y_{1:T},\Upphi^{( j-1) }\right] }{T}=\frac{\sum_{t=1}^{T}\Pr(x_{t}=i \vert y_{t},\Upphi^{(j-1)}) }{T}, $$

(1)

$$ m_{i}^{(j)} =\frac{\sum_{t=1}^{T}{\mathbb{E}}\left[ y_{t}\delta_{i}(x_{t})\vert y_{1:T},\Upphi^{( j-1)}\right] }{\sum_{t=1}^{T}{\mathbb{E}}\left[\delta _{i}( x_{t}) \vert y_{1:T},\Upphi^{( j-1) }\right] }=\frac{\sum_{t=1}^{T}y_{t}\Pr(x_{t}=i \vert y_{t},\Upphi^{(j-1) }) }{T\pi_{i}^{( j)}}, $$

(2)

$$ \begin{aligned} \Upsigma_{i}^{(j)} & =\frac{\sum_{t=1}^{T}{\mathbb{E}}\left[y_{t}y_{t}^{\rm T}\delta_{i}(x_{t})\vert y_{1:T},\Upphi^{( j-1)}\right] }{\sum_{t=1}^{T}{\mathbb{E}}\left[ \delta_{i}(x_{t})\vert y_{1:T},\Upphi^{( j-1) }\right] }-m_{i}^{(j) }m_{i}^{( j) {\rm T}}\\ & =\frac{\sum_{t=1}^{T}y_{t}y_{t}^{\rm T}\Pr( x_{t} =i \vert y_{t},\Upphi^{(j-1)}) }{T\pi_{i}^{(j)}}-m_{i}^{( j) }m_{i}^{(j) {\rm T}}. \end{aligned} $$

(3)

2.2.2 Recursive EM

In a recursive framework, we want to be able to update the parameter estimate $\Upphi^{(t)}$ at the time index t based on the new observation y _t . Most of the recursive EM algorithms proposed in the literature rely on updates of the form [12, 17, 18]

$$ \Upphi^{(t)}= (1-\gamma_{t}) \Upphi^{( t-1)}+\gamma_{t}I(\Upphi^{( t-1)})\nabla\log g (y_{t}\vert \Upphi) \vert _{\Upphi^{(t-1)}} $$

(4)

where $I(\Upphi^{(t-1)})$ is the complete Fisher information matrix and {γ _t } is a non-decreasing stepsize sequence. The main issue with this approach is that if some components of the parameter $\Upphi$ are restricted to a manifold then the update (4) does not guarantee they will remain in this manifold. This is, for example, the case for the Gaussian mixture models where $(\pi_{1},\ldots,\pi_{k})$ have to lie on the simplex and $(\Upsigma_{1},\ldots,\Upsigma_{k})$ have to be positive definite. To handle these problems, a standard approach requires the use of reprojection algorithms or the use of an alternative parameterization. This is not elegant and can perform poorly in practice.

The general algorithm we are proposing here is inspired from [1] (see also for a related approach [16]). It bypasses elegantly these problems by directly working with the sufficient statistics appearing in the standard batch EM algorithm. If we denote by S(x, y) the sufficient statistics appearing in the EM algorithm, i.e. for multivariate Gaussian mixtures

$$ S(x,y)= (\delta_{1}(x),\ldots,\delta _{k}(x) ,y\delta_{1}(x) ,\ldots,y\delta_{k}(x),yy^{\rm T}\delta_{1}( x) ,\ldots,yy^{\rm T} \delta_{k}(x)), $$

(5)

then we simply use the following modified recursive Expectation update:

$$ S^{(t)}=(1-\gamma_{t})S^{( t-1) }+\gamma_{t}{\mathbb{E}}[S( x_{t},y_{t})\vert y_{t},\Upphi^{(t-1) }]. $$

(6)

Then given S ^(t), we use the standard M-step of the EM algorithm to obtain $\Upphi^{(t)}.$ The algorithm is thus a minor modification of the standard EM algorithm and does require neither reprojection nor reparameterization.

In practice we use γ _t  = t ^−α for 0.5 < α ≤ 1. This algorithm can be rewritten as a stochastic approximation algorithm minimizing the Kullback–Leibler distance over θ between the distribution of the observations and the parametric family $\{g(y\vert \Upphi) ;\Upphi\in\varvec{\Upphi}\}.$ A proof of convergence relying on stochastic approximation is sketched in [16] (see [5] for an introduction).

Example 1 (continued)

In the multivariate Gaussian case, the sufficient statistics are given by (5) and thus the update (6) proceeds as follows: we have

$$ S^{(t)}=\left(a_{1:k}^{(t)},b_{1:k}^{( t)},c_{1:k}^{(t) }\right) $$

where

$$ a_{i}^{(t) } =(1-\gamma_{t}) a_{i}^{( t-1) }+\gamma_{t}\Pr( x_{t}=i\vert y_{t},\Upphi^{(t-1)}), $$

(7)

$$ b_{i}^{(t)} =(1-\gamma_{t}) b_{i}^{(t-1)}+\gamma_{t}y_{t}\Pr( x_{t}=i\vert y_{t},\Upphi^{(t-1)}), $$

(8)

$$ c_{i}^{(t)} =(1-\gamma_{t}) c_{i}^{(t-1) }+\gamma_{t}y_{t}y_{t}^{\rm T}\Pr(x_{t} =i \vert y_{t},\Upphi^{(t-1)}). $$

(9)

and we use

$$ \pi_{i}^{(t)}=\frac{a_{i}^{(t) }}{\sum _{j=1}^{k}a_{j}^{(t)}}, $$

(10)

$$ m_{i}^{(t)}=\frac{b_{i}^{(t)}} {a_{i}^{(t)}}, $$

(11)

$$ \Upsigma_{i}^{(t)}=\frac{c_{i}^{(t)}} {a_{i}^{(t)}}-m_{i}^{(t)}m_{i}^{( t) {\rm T}}.$$

(12)

3 Dirichlet process mixtures and EM algorithms

3.1 Dirichlet process mixtures

The previous examples assume that the number of components of the mixture is fixed and known. However, in practice the number of components is often unknown and needs to be estimated from the data. To achieve this, we rely on DPM models which are a very popular class of models in the literature (see for example [4, 10]). In this model, we have

$$ g(y\vert \Upphi)=\sum_{i=1}^{\infty}\pi_{i} f_{i}(y\vert \theta_{i}) $$

where the infinite sequence of weights {π _i } is defined as follows: we have π₁ = v ₁ and for i > 1

$$\pi_{i}=v_{i}{\prod\limits_{j=1}^{i-1}}( 1-v_{j}) $$

(13)

where {v _i } is an infinite sequence of i.i.d. random variables distributed according to a beta distribution of parameters (1, α). Here α is an hyperparameter such that the higher α the higher the number of significant components. Equation 13 corresponds to the so-called stick-breaking prior representation of the Dirichlet process [10]. In the rest of the paper, we will always consider α ≥ 1; this corresponds to selecting a bounded prior density for v _i . The selection of the parameter α has a crucial influence on the inference results and we present in the next section a principled approach to select it automatically from the data.

For sake of implementation, we will consider here a truncated Dirichlet prior where we select a large value N and we set v _N  = 1. It is shown in [10] than even for very large datasets this truncation has virtually no effect if N is taken reasonably large, i.e. N = 100. In this case the parameter $\Upphi$ of interest is given by $\Upphi=(v_{1:N-1},\theta_{1:N}).$

3.2 Batch and recursive EM algorithms for truncated DPMs

Inference in DPMs models is usually performed using MCMC methods [10] or VB approaches [4]. For very large datasets, these approaches remain too computationally intensive. We show here how we can simply apply the batch and recursive EM algorithms in this framework when the parameter α is given and then discuss a procedure to estimate it automatically from the data.

3.2.1 Batch EM

Given the observations y _1:T we want to estimate $\Upphi=(v_{1:N-1},\theta_{1:N}).$ In this case, we have

$$ \begin{aligned} Q(\Upphi,\Upphi^{(j-1)}) & \equiv\sum_{n=1}^{T}( \log f_{1}(y_{n}\vert \theta_{1}) +\log v_{1}) \Pr(x_{n}=1\vert y_{n},\Upphi^{(j-1)}) \\ &\quad +\sum_{k=2}^{N}\sum_{n=1}^{T}\left(\log f_{k}( y_{n}\vert \theta_{k}) +\log v_{k}+\sum_{l=1}^{k-1}\log (1-v_{l})\right) \Pr( x_{n}=k\vert y_{n} ,\Upphi^{(j-1)})\\ &\quad +\sum_{k=1}^{N-1}(\alpha-1) \log( 1-v_{k})\\ & =\sum_{k=1}^{N}\left(\sum_{n=1}^{T}\log f_{k}( y_{n}\vert \theta_{k})\Pr( x_{n}=k\vert y_{n},\Upphi^{(j-1)})\right)\\ &\quad +\sum_{k=1}^{N-1}\log v_{k}\left[ \sum_{n=1}^{T}\Pr( x_{n}=k\vert y_{n},\Upphi^{(j-1)}) \right]\\ &\quad +\sum_{k=1}^{N-1}\log(1-v_{k}) \left[ \alpha-1+\sum _{l=k+1}^{N}\sum_{n=1}^{T}\Pr( x_{n}=l\vert y_{n} ,\Upphi^{(j-1)}) \right] \end{aligned} $$

where ≡ means “equal” up to an additive constant independent of the first argument of Q.

By maximizing this expression in v _i we obtain

$$ v_{i}^{(j) }=\frac{\sum_{n=1}^{T}\Pr( x_{n}=i\vert y_{n},\Upphi^{(j-1)}) }{\sum_{n=1} ^{T}\Pr(x_{n}=i\vert y_{n},\Upphi^{(j-1) }) +\alpha-1+\sum_{l=i+1}^{N}\sum_{n=1}^{T}\Pr( x_{n}=l\vert y_{n},\Upphi^{( j-1)})} $$

(14)

as we have set α ≥ 1. From the expression of v ^(j)_1:N−1 , we can compute the weights π ^(j)_1:N using (13). The expressions for the other parameter updates θ_1:N are similar to the standard finite mixture case.

3.2.2 Recursive EM

The recursive EM algorithm can also be implemented straightforwardly in the DPM case. To update the parameters θ_1:N , we use the same update equations as for the recursive EM algorithm described previously. To update π ^(t)_1:N , we simply compute a ^(t)_1:N−1 recursively in time using (7). Based on a ^(t)_1:N−1 , we obtain the estimates v ^(t)_1:N−1 using

$$ v_{i}^{(t)}=\frac{a_{i}^{(t) }}{a_{i}^{(t)}+\alpha-1+\sum_{l=i+1}^{N}a_{l}^{( t)}} $$

From these estimates we obtain the estimates of π ^(t)_1:N using (13).

3.2.3 Learning the parameter α

We show here that it is also possible to come up with modified EM algorithms which updates the parameter α by maximizing an approximation of the marginal likelihood of α. In the batch case, this proceeds as follows:

Ideally, we would like to also implement an EM type procedure to maximize the marginal likelihood of the observations with respect to α. Assume $\Upphi$ is known for the time being, then an EM algorithm would proceed as follows:

$$ \alpha^{(j) }=\underset{\alpha}{\arg\max} Q(\alpha,\alpha^{(j-1)}) $$

where

$$ Q(\alpha,\alpha^{(j-1)}) ={\mathbb{E}}[\log f( x_{1:T},y_{1:T}\vert \alpha,\Upphi) \vert y_{1:T},\alpha^{(j-1)},\Upphi]. $$

After a few calculations, we obtain

$$ Q(\alpha,\alpha^{(j-1)}) =(N-1) \log\alpha +\sum_{k=1}^{N-1}{\mathbb{E}}[\log {\mathcal{B}}(C_{k}( x_{1:T}) +1,C_{>k}( x_{1:T})+\alpha) \vert y_{1:T},\alpha^{( j-1)},\Upphi]+C $$

(15)

where C is a constant independent of α, C _i (x _1:T ) is the number of latent variables equal to i,C _>i (x _1:T ) the number of latent variables strictly superior to i and $\mathcal{B}(u,v)$ is the Beta function defined for u,v > 0 by

$$ {\mathcal{B}}(u,v) =\int\limits_{0}^{1}t^{u-1}(1-t) ^{v-1}{\hbox{d}}t. $$

Unfortunately, computing Q(α, α^(j−1)) has complexity $\mathcal{O}(T^{N}).$ Using the convexity of the log-Beta function [8], it is, however, possible to establish that

$$ \begin{aligned} &\sum_{k=1}^{N-1}{\mathbb{E}}[\log {\mathcal{B}}(C_{k}(x_{1:T}) +1,C_{\!>\!k}( x_{1:T}) +\alpha)\vert y_{1:T},\alpha^{(j-1)},\Upphi]\\ &\quad\geq\sum_{k=1}^{N-1}\log {\mathcal{B}}( \overline{C} _{k}+1,\overline{C}_{\!>\!k}+\alpha). \end{aligned} $$

where

$$ \begin{aligned} \overline{C}_{k} & ={\mathbb{E}}[C_{k}( x_{1:T})\vert y_{1:T},\alpha^{(j-1)},\Upphi] , \\ \overline{C}_{\!>\!k} & ={\mathbb{E}}[C_{\!>\!k}( x_{1:T}) \vert y_{1:T},\alpha^{(j-1)},\Upphi]. \end{aligned} $$

We propose to approximate Q(α,α^(j−1)) by

$$ Q(\alpha,\alpha^{(j-1)})\approx( N-1) \log\alpha+\sum_{k=1}^{N-1}\log{\mathcal{B}}( \overline{C}_{k}+1,\overline{C}_{>k}+\alpha). $$

Finally, to maximize this approximate Q(α, α^(j−1)), we used a fixed-point iteration in the spirit of [15] where we update

$$ \alpha\leftarrow\frac{N-1}{\sum_{k=1}^{N-1}\Uppsi (\overline{C} _{k}+\overline{C}_{\!>\!k}+\alpha) -\Uppsi (\overline{C}_{\!>\!k} +\alpha)} $$

where $\Uppsi(x) =\frac{{\hbox{d}}\Upgamma(x)}{{\hbox{d}}x}$ is the digamma function, that is the derivative of the $\log\,\Upgamma(x)$ function.

In the batch case, we alternative update steps for α and standard update steps for $\Upphi.$ In the on-line case, we only update α after each pass on the data where $\Upphi$ is updated.

4 Simulation results

In order to assess the proposed model and algorithms, it will be necessary to examine the following:

• 1. estimation accuracy and computational complexity

• 2. ability of the proposed EM for DPM model against finite mixture models

• 3. competitiveness against other inference methods for DP, e.g., VB

• 4. estimation capability of scale parameter.

The proposed batch EM algorithm for DPM performs well in the experiments reported below. It would also be worth conducting performance comparison of batch and recursive EM algorithms since the latter is an interesting alternative to the former. Specifically, the following experiments are conducted using synthetic data:

• Section 4.1 compares batch and recursive EM algorithms in terms of estimation accuracy and computational complexity. In order to make the comparison clear, the underlying mixture model is finite.

• Section 4.2.1 examines the performance of the proposed batch EM for DPM model instead of finite mixture model. In order not to blur the comparison, we first fix α. Estimation of α is reported in Sect. 4.3 below.

• Section 4.2.2 compares the proposed recursive EM algorithms for DPM model with standard recursive EM algorithm for finite mixture model.

• Section 4.2.3 compares the proposed EM algorithm for DP with VB, another iterative maximization based algorithm.

After these comparisons, we use the EM algorithm with DPM to perform image segmentation. Finally, we demonstrate the performance of the EM algorithm with DPM in an image classification context.

4.1 Batch versus recursive EM for finite mixture models

We consider a mixture of three two-dimensional Gaussian distributions with parameters π₁ = π₂ = 0.3, π₃ = 0.4, 

$$ \begin{aligned} m_{1} &=\left( \begin{array}{l} 3\\ 3 \end{array} \right),\quad m_{2}=\left(\begin{array}{l} -3\\ 3 \end{array}\right),\quad m_{3}=\left(\begin{array}{l} 0\\ -3 \end{array}\right),\\ \Upsigma_{1} &= \left( \begin{array}{ll} 1 & -0.5\\ -0.5 & 1 \end{array}\right),\quad \Upsigma_{2}=\left( \begin{array}{ll} 1 & 0.5\\ 0.5 & 1 \end{array}\right),\quad \Upsigma_{3}=\left(\begin{array}{ll} 1 & 0\\ 0 & 0.5 \end{array}\right). \end{aligned} $$

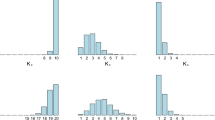
This is a rather simple problem where the components only mildly overlap. We simulated 10,000 data points from this mixture and compare the results on the batch and recursive EM algorithms by running 1,000 realizations of both algorithms. For each realization, the initialization is random but similar for the batch and recursive EM algorithms. We run the recursive algorithm only once while we perform 30 iterations of the batch algorithms. In Fig. 1, we display the histogram in red of the log-likelihood of the parameter estimates for these 100 realizations associated with the batch algorithm for 1, 10, 20, and 30 iterations and the histogram in blue obtained using one single pass through the data for the recursive algorithm.

Fig. 1

Histograms of log-likelihood of the estimates for 100 realizations: one single pass on-line EM (blue) versus batch EM (red) after 1 (up left), 10 (up right), 20 (bottom left) and 30 (bottom right) iterations

We see that essentially half the realizations of the recursive EM algorithm converge toward the same mode as the batch EM algorithm. The computational complexity of a pass of the batch EM is in $\mathcal{O}(Tkd^{2}+kd^{3})$ whereas it is in $\mathcal{O}(Tkd^{3})$ for the recursive EM algorithm.¹ As the recursive EM converges much faster then this suggests that an efficient approach to perform parameter estimation for very large datasets consists of using a small run of the recursive EM algorithm and picking the parameter estimate associated with the highest likelihood instead of iterating a standard batch EM algorithm.

4.2 Σ versus DPM

In many scenarios, we do not know the number of components of the mixture. In this context, we can try to either fit a standard finite mixture model with a large number k of components, say k = 100. Alternatively, we can fit a (truncated) DPM model with say N = 100. The DPM model penalizes implicitly models with a large number of components, whereas the standard finite mixture model does not include such a penalty term.

4.2.1 Batch EM algorithm

We consider the same parameters as in the previous experiment but only 1,000 datapoints. In order to assess the performance of the proposed EM for DPM, in the first place, we perform experiments with α fixed first. We fit the DPM model with an empirical value α = 2 (α = 1 yields very similar results) which the authors had obtained through preliminary experiments and run the batch EM algorithm. Since the experiments to be reported below are successful, the next issue would be to estimate α automatically. In Sect. 4.3 below, α is estimated using the procedure discussed in Sect. 3.2.3.

After 100 iterations the parameters associated with those components with the largest mixture parameters (relabeled 1,2,3 for convenience) are given by

$$ \begin{aligned} \widehat{\pi}_{1} &=0.3,\quad \widehat{\pi}_{2}=0.29, \quad\widehat{\pi}_{3}=0.41,\\ \widehat{m}_{1}&=\left( \begin{array}{l} -3.03\\ 2.95 \end{array} \right), \quad\widehat{m}_{2}=\left( \begin{array}{l} 2.91\\ 3.08 \end{array} \right),\quad \widehat{m}_{3}=\left( \begin{array}{l} -3.74\\ 2.96 \end{array} \right) ,\\ \widehat{\Upsigma}_{1} &=\left( \begin{array}{ll} 1.32 & 0.42\\ 0.42 & 0.83 \end{array}\right), \quad\widehat{\Upsigma}_{2}=\left( \begin{array}{ll} 1.34 & -0.36\\ -0.36 & 0.72 \end{array} \right), \quad\widehat{\Upsigma}_{3}=\left( \begin{array}{ll} 0.93 & 0\\ 0 & 0.49 \end{array}\right). \end{aligned} $$

The parameters are satisfactorily estimated. We display in Fig. 2 the estimates of π_1:100 and in Fig. 3 the estimates of the components of m _1:100 as a function of the iteration number.

Fig. 2

Estimates of π_1:100

Fig. 3

Estimates of the components of m _1:100

We next consider a more difficult problem where π₁ = π₂ = 0.3, π₃ = 0.4, 

$$ \begin{aligned} m_{1} &=\left( \begin{array}{l} 2\\ 2 \end{array} \right),\quad m_{2}=\left( \begin{array}{l} -2\\ 2 \end{array}\right),\quad m_{3}=\left( \begin{array}{l} 0\\ -1 \end{array} \right),\\ \Upsigma_{1} &=\left(\begin{array}{ll} 1 & -0.5\\ -0.5 & 1 \\ \end{array}\right), \quad\Upsigma_{2}=\left( \begin{array}{ll} 1 & 0.5\\ 0.5 & 1 \\ \end{array}\right),\quad \Upsigma_{3}=\left(\begin{array}{ll} 1 & 0\\ 0 & 0.5 \end{array}\right). \end{aligned} $$

Compared with the previous example, the components overlap significantly. Figure 4 demonstrates the estimated π_1:100. The algorithm still appears functional. This example will also be used in the following argument:

Fig. 4

Estimates of π_1:100 for the mixture with more overlap

4.2.2 Recursive EM algorithm

We simulated 10,000 data points from the second example in the previous section with more overlap than the first one. We ran 100 realizations of both the recursive EM for finite mixture model and for DPM model. For each realization, the initialization is random but similar for the two recursive EM algorithms. Out of these 100 runs, 35 runs of the recursive EM for DPM gave only three π _i such that π _i  > 0.05 among π_1:100, whereas only one run of the recursive EM for the standard finite model provided such a result. The recursive EM algorithm associated with the standard finite mixture model fails spectacularly in many cases by fitting far too many components or a single one. The recursive EM for DPM provides far more reasonable and reliable results in all the experiments we conducted.

4.2.3 EM versus variational inference for DPM

In a Bayesian framework, we assign a prior distribution to the parameters of interest and inference relies on the associated posterior distribution. Unfortunately, the posterior distribution does not admit a closed-form expression and needs to be approximated. A standard approach consists of using iterative sampling algorithms such as MCMC methods but these techniques are computationally expensive [2]. An alternative method to approximate the posterior is variational Bayes (VB) [3, 20]. VB provides an analytical approximation to the posterior which is obtained by maximizing a lower bound of the marginal likelihood. VB has become very popular over the past few years and has been recently applied to DPM [4].

We compare here the batch EM algorithm to VB approximations for standard finite mixture of Gaussians and DPM. We apply all the algorithms to synthetic data obtained from a mixture of seven two-dimensional Gaussian distributions with parameters π₁ = π₂ = π₃ = π₄ = π₅ = π₆ = 0.14, π ₇ = 0.16 and

$$ \begin{aligned} \mu_{1}=\left( \begin{array}{l} -5.0\\ 0.0 \end{array} \right),\quad \mu_{2}=\left( \begin{array}{l} -5.0\\ 5.0 \end{array}\right), \quad \mu_{3}=\left( \begin{array}{l} 0.0\\ 5.0 \end{array} \right), \quad \mu_{4}=\left( \begin{array}{l} 5.0\\ 5.0 \end{array} \right), \quad \\ \mu_{5}=\left( \begin{array}{l} 5.0\\ 0.0 \end{array} \right),\quad \mu_{6}=\left( \begin{array}{l} 5.0\\ -5.0 \end{array} \right), \quad \mu_{7}=\left( \begin{array}{l} 3.0\\ 7.0 \end{array} \right) \\ \Upsigma_{1}=\Upsigma_{2}=\left( \begin{array}{ll} 1.0 & 0.0\\ 0.0 & 3.0 \end{array} \right),\quad \Upsigma_{3}=\Upsigma_{4}=\left( \begin{array}{ll} 3.0 & 0.0\\ 0.0 & 1.0 \end{array} \right) \\ \Upsigma_{5}=\Upsigma_{6}=\Upsigma_{7}=\left( \begin{array}{ll} 1.5 & 0.5\\ 0.5 & 3.0 \end{array} \right). \end{aligned} $$

We simulated 100 data points from this mixture to estimate parameters. Initialization of the parameters and hyperparameters was the same in both algorithms, except for the prior on α. In VB, we assumed the gamma prior for α with mean 2.0. We ran the batch EM algorithm with α set equal to 2.0. We also ran the batch and on-line EM algorithms which estimate α using the procedure discussed in Sect. 3.2.3. We truncate the DPM model at N = 100 for both the VB and EM algorithms. For the joint prior distribution on the mean and covariance parameters, we used an inverse-Wishart normal.

We assess the performance of the EM and VB algorithms by comparing the Kullback–Leibler distance between the true distribution and the observations $p(y|\Upphi_{\rm true})$ and the predictive distribution p(y|y _1:T ) estimated through the algorithms. We have

$$ {\hbox{KL}}=\int p(y|\Upphi_{\rm true})\log\frac{p(y|\Upphi_{\rm true})}{p(y|y_{1:T})} {\hbox{d}}y\approx\frac{1}{P}\sum_{k=1}^{P}\frac{p(y_{k}^{\ast}|\Upphi_{\rm true})} {p(y_{k}^{\ast}|y_{1:T})} $$

where $\{y_{k}^{\ast}\} _{k=1,\ldots,P}$ are sampled from $p(y|\Upphi_{\rm true}).$ We use P = 500 in our experiments. For the EM algorithm, we use

$$ p(y_{k}^{\ast}|y_{1:T})\approx p(y_{k}^{\ast}|\hat{\Upphi}) $$

where $\hat{\Upphi}$ is the MAP parameter estimate. For VB, we use

$$ p(y_{k}^{\ast}|y_{1:T})\approx\int p(y_{k}^{\ast}|\Upphi)q(\Upphi|y_{1:T}){\hbox{d}}\Upphi, $$

where $q(\Upphi|y_{1:T})$ is the variational posterior. The results are presented in Fig. 5 below. In this example, EM outperforms significantly VB.

Fig. 5

Kullback–Leibler distance for predictive density estimates using EM and VB. MAP denotes MAP EM, while VB denotes variational inference without DPM; MAPX denotes the fact that the number of components is fixed to X. DPMAP and DPVB indicate MAP and VB with DPM. α = 2.0 means that α is fixed at 2.0, whereas α = Auto means that α is estimated from the data

Figure 5 shows the Kullback–Leibler distance for predictive density estimates associated with

• batch EM for DPM model with α fixed at 2.0 (denoted by DPMAP a = 2.0)

• batch EM for DPM model with α estimated (denoted by DPMAP a = Auto)

• recursive EM for DPM model with α estimated (denoted by DPMAP recursive)

• VB for DPM model with α fixed at 2.0 (denoted by DPVB a = 2.0)

• VB for DPM model with α learned (denoted by DPVB a = Auto).

The proposed batch and recursive EM for DPM model outperformed VB at least in this experiment. For a reference purpose, Fig. 5 also gives box plots of the Kullback–Leibler distance associated with

• batch EM for finite mixture model with the number of components fixed at 5, 10, and 20, respectively (denoted by MAP5, MAP10, and MAP20)

• VB for finite mixture model with the number of components fixed at 5, 10, and 20, respectively (denoted by VB5, VB10, and VB20).

From the experiments performed in this section, we have the following observations:

• 1. The proposed batch EM algorithm for DPM model captured the true parameters well as demonstrated in Sect. 4.2.1.

• 2. The proposed recursive EM algorithm for DPM model outperformed the standard recursive EM algorithm for finite mixture model as shown in Sect. 4.2.2.

• 3. The proposed batch and recursive EM algorithms for DPM model outperformed VB algorithm as demonstrated in Sect. 4.2.3.

• 4. The batch and the recursive EM algorithms with α estimation are also competitive.

• 5. The proposed algorithm gave reasonable results on image segmentation and image classification problems.

The two figures in Fig. 6 display the estimated mixture components with DPM and VB. Crosses and dotted ellipses, respectively, indicate the mode of the mean and covariance of each component. We only display components with mixing weights π _i  ≥ 0.0001.

Fig. 6

Estimated components using VB

Note that when the components are truncated at N, there are N parameter vectors, $(\pi_i,\theta_i),\;i=1,\ldots,N$ estimated by the proposed EM algorithm. The thresholding was simply introduced to ease the presentation of the results. This same is also applied to other experiments. Note also that the VB estimate gives rise to a spurious component near the center of the dataset. Another two figures in Fig. 7 show the mixing weights estimated by DPM and VB.

Fig. 7

Mixing weights using VB for DPM model

4.3 Image segmentation

We present an application of our algorithm to image segmentation [13]. Each pixel corresponds to a point in ${\mathbb{R}^{3};}$ each component corresponds to a specific color R, G or B. We build a Gaussian mixture model for the distribution of the pixels. We then estimate the number of significant components (i.e. whose estimated mixing weights π _i is such that π _i  > 0.01) and the parameters of these components using the DPM model and the EM algorithm. Each pixel is then attributed to the component having the highest posterior probability.

We apply this algorithm to an image taken from Berkeley Segmentation Dataset (BSDS No. 253036). The size of the image is 481 × 321; hence this corresponds to 154,401 observations. After having applied the batch EM algorithm to this dataset, we identified 16 significant components. We display in the original image in Fig. 8 and its segmented version in Fig. 9.

Fig. 8

Original image

Fig. 9

Segmented image using DPM model

While image segmentation algorithm often involves detailed high-level operations, the method used in the present experiment is a simple RGB component clustering, and yet it appears to have captured at least several important segmented components. Observe that the tree and the elephants are segmented in a relatively crisp manner. The algorithm also appears to have captured the segmented sky as well as the clouds. The textures associated with the foreground grasses are also discernible. More specifically, all the elephants belonged to the same class with mixing parameter 0.04 where average value of (R, G, B) is (72, 76, 68). This class also contained the tree in the center. The sky consisted of four components:

• mixing parameter = 0.34, (R, G, B) = (173, 197, 230)

• mixing parameter = 0.17, (R, G, B) = (212, 229, 242)

• mixing parameter = 0.11, (R, G, B) = (177, 190, 216)

• mixing parameter = 0.06, (R, G, B) = (236, 253, 254).

The foreground grasses consisted of two components:

• mixing parameter = 0.08, (R, G, B) = (95, 102, 57)

• mixing parameter = 0.07, (R, G, B) = (115, 113, 63).

4.4 Image classification

Our aim is to classify some images based on PCA-SIFT features [11]. We selected five categories from the Caltech Database [9]: airplanes, cars, faces, leaves, and motorbikes. Figure 10 shows some of the images from the dataset.

Fig. 10

A few images from the Caltech database

For each category $C\in\{1,2,3,4,5\},$ we approximate the distribution of the features using a Gaussian DPM model using 100 training data, i.e. we estimate a vector of parameter $\Upphi_{\rm C}$ using the EM algorithm. For each new image, we then extract a vector of features and compute its likelihood for each of the possible Gaussian DPM model. We select the category of the new image as the one corresponding to the highest likelihood.

For each category, we use 50 test images. Given an image, the PCA-SIFT detects 50–300 features points and a 36-dimensional vector is associated with each feature point. To reduce the computational cost and the number of parameters, we use only diagonal covariance matrices with N = 100 and α = 2.0 for the mixture model. The result was compared with a standard bag-of-features model using a naive Bayes classifier where the feature vectors are discretized using a K-means algorithm [6]. For example, in Fig. 11, K = 100 means that the number of discretized features is 100.

Fig. 11

Classification accuracy of the two algorithms. DP corresponds to the proposed EM algorithm for Gaussian. K − x indicates naive Bayes with x discretized features

The results are displayed in Fig. 11.

Figure 11 indicates that, at least in this example, the proposed algorithm achieves the highest accuracy. Figure 12 illustrates some of the classification results. The red circles represent PCA-SIFT features. The rightmost picture, which was incorrectly categorized by the proposed algorithm, appears to carry several feature points around the building in the back.

Fig. 12

Test images: the first four are correctly classified as airplanes, the fifth one is misclassified

5 Discussion

DPM models have become a very popular class of statistical models to perform inference in mixture models when the number of components is unknown. Standard approaches to fit DPM rely either on MCMC or VB methods.

Note that MCMC computation requires typically several thousand iterations [2]. Our experience on VB tells us that a typical VB needs 15–30 iterations before convergence. Since the proposed recursive EM is a single pass scheme, it is less expensive than MCMC and VB.

In order to consider the complexity of VB, note that the iteration formula for the basic parameters of VB are similar to those of batch EM given in (1)–(3) (Sect. 2). Therefore, the complexity of the covariance matrix statistics computation is of order O(Tkd ²). For the computation of the test distribution q(z), there are k log  determinants as well as k inverse  matrix computations. This gives rise to O(kd ³). Adding those two, we have O(Tkd ² + kd ³) for the complexity of VB which is the same as the complexity of the batch EM described in Sect. 4.1.

We have proposed here original EM-type algorithms to fit DPM models. These batch and recursive EM algorithms are computationally efficient and perform well in the set of experiments we have conducted. We believe that these methods complement the current set of tools available to fit DPM and are an attractive alternative.