1 Introduction

Tortuosity is an important parameter used e.g. to determine the pressure drop occurring during fluid flows through porous media. This quantity was introduced by Kozeny [1] for the correction of the hydraulic drop and next it was used again by Carman [2] for the modification of the value of the filtration velocity. In both improvements mentioned it has been used the observation, that the real path length (\(L_p\)) of the fluid inside a porous medium is greater than the measurement section (\(L_0\)). In the literature one can find many papers related to the investigations of this quantity with the use of experimental (e.g. [3–7]), analytical (e.g. [8–11]) or numerical methods (e.g. [12–15]). In many investigations a direct correlation between tortuosity and porosity is assumed (e.g. [16–19]). It was stated that the tortuosity decreases if the porosity increases [20–22]. Since the determination of the tortuosity value in real porous media is not obvious, the use of an analytical formula is still the easiest way to obtain a value, which in turn may be used for other purposes, e.g. for calculating the pressure drop from the Kozeny-Carman equation. It should be highlighted that the use of an analytical formula gives the result of one value only, which is representative for the whole porous medium.

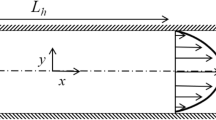
The tortuosity is defined as the ratio of the actual path length inside pore channels \(L_p\) [m] to the thickness of porous medium \(L_0\) [m] [23]

$$\begin{aligned} \tau =\frac{L_p}{L_0} \end{aligned}$$
(1)

It is important that in a general case path length \(L_p\) in the formula (1) may be understood as a geometrical quantity \((L_p^g)\) or as a flow property, the so-called hydraulic tortuosity \((L_p^h)\) (Fig. 1).

Fig. 1
figure 1

The visualization of the tortuosity definition: a geometric, b hydraulic

Full size image

In the geometric approach only the channel geometry is important and the fluid flow through the porous medium is not taken into account (the fact is represented by the zero value of filtration velocity \(v_f\) in the Fig. 1a). The geometric tortuosity may be obtained with the use of experimental (CT/IA techniques [3, 7, 24], acoustic [4–6], electrical [22] and others [25]), analytical [11, 16, 17] or computational methods [26, 27]. As a result one or many values of the tortuosity may be obtained. In the second case, an average value representative for the whole bed is usually calculated. The main advantage of this approach is that the motion equations of the fluid don’t need to be solved.

If the fluid flow through the porous medium is investigated (the fact is represented by a positive value of filtration velocity in Fig. 1b) and the velocity field of this flow is known, path length \(L_p^h\) may be calculated on the basis of velocity components [12, 20]. In this approach not the pure geometry of the channel but the streamlines plays the key role. Details about the fluid flow inside a porous medium may be obtained experimentally (e.g. by the use of the Particle Image Velocimetry [28, 29]) or numerically (usually by the use of the Finite Volume Method [13, 30], the Lattice-Boltzmann Method [12, 20] or the Immersed Boundary Method [31]). The main advantage of this approach is that the tortuosity may be calculated locally in the whole velocity field and in consequence the 3D tortuosity field may be obtained (or one averaged value). However, the size of the sample is here strongly limited: by the resolution of sensors in the experimental methods and by the available computational power in the numerical approach. Currently only relatively small bed samples may be investigated by the use of such ways.

This article concerns a computational method destined for obtaining the geometric tortuosity in polydisperse granular beds consisting of spherical or quasi-spherical particles, freely distributed in the 3D space. The main aim is to show a new way of calculating the tortuosity distribution in the plane perpendicular to the chosen direction in the space (interpreted as the main flow direction) by the use of own computational algorithm. This concept links the main advantages of both approaches of the tortuosity meaning described above: the ability to analyze relatively large granular beds due to low demand for computing power and the possibility to obtain of the tortuosity distribution in the space. Although this distribution is not three-dimensional, may be useful for estimation of the local pressure drops in fluid flows through granular bed, particularly if only one flow direction is analysed. To reach the article aim the so-called Path Tracking Method (PTM), developed by the author in the year 2009 and recently improved, is applied here. In the report [27] and paper [32], the mathematical basis of the PTM were shown as well as the first experimental verification of this approach. In the work [33], a mathematical modification of the PTM was described. In further investigations a discussion on the similarities and differences in the geometric and hydraulic tortuosity was performed. It was shown that PTM gives similar results, namely the average value as well as the tortuosity distribution curve, to the simulations with the use of the Lattice-Boltzmann Method, in which the hydraulic tortuosity was calculated. In the paper [34], different porosity-tortuosity correlations were collected and used for calculating the tortuosity. By comparing the results obtained for the same data, some new conclusions were stated there.

The structure of the paper is as follows: first a short description of the PTM is presented. Then, two approaches of the application of this method are analysed: a standard approach, in which the tortuosity values in a few chosen locations are calculated; and a new approach, which leads to obtaining the tortuosity field for the whole bed. Finally, a comparison of the two approaches in the context of two examples is presented and discussed. At the end a basic statistical analysis of the obtained results is shown.

Fig. 2
figure 2

Schematic representation of the PTM (particles are not in a scale)

Full size image

2 The Path Tracking Method

2.1 General description

The Path Tracking Method (PTM) is an iterative method of determination of the length of a pore channel in a porous medium in a chosen space direction, which consists in analysing the local structure of the pore space based on vector geometry. Path \(L_p^g\) is understood here as the shortest continuous line between any two points within the pore space, according to the idea mentioned in the paper [20]. The PTM method was developed as a tool destined for investigating the spatial structure of granular beds. As a result, the numerical code called PathFinder was written [35, 36]. The length of a pore channel in the PTM is determined between two parallel planes based on the sum of the unitary lengths. This method is based on the so-called tetrahedral structures that establish the basis for the calculation algorithm. Tetrahedral structures are created based on the data on the location and diameter of each particle in the bed. Such data may be obtained from the Discrete Element Method (DEM) simulation or from the analysis of a set of tomography scans. Details concerning PTM are available in e.g. the PathFinder User’s Guide [36].

Fig. 3
figure 3

Locations of the ISP in the bottom surface of the bed for cubical (left) and cylindrical domains (right), respectively

Full size image

2.2 Algorithm

In the PTM the key role is played by tetrahedral structures formed by four adjacent particles. If such a structure is defined, the analysis of the local spatial arrangement of the particles is than possible. The description of the PTM may be found in the following papers [27, 32, 33, 36, 37] and that is why it is not described in detail in the hereby article. The algorithm for calculating path length \(L_p^g\) may be summarized as follows (Fig. 2):

  • Arbitrarily choose the Initial Starting Point (ISP) at the bottom of the porous bed;

  • Find three particles (P1, P2 and P3) which are nearest to the ISP and which form a triangle in the space;

  • Calculate the coordinates of the gravity centre (GC) of the surface (in the triangle plane) through which fluid flows;

  • Move the Initial Starting Point to the Final Starting Point (FSP)—in this way the first path section is perpendicular to the bottom surface of the bed;

  • Calculate the normal to the triangle;

  • Estimate coordinates of the so-called Ideal Location (IL), in which the next sphere (P4) surrounding the path should be located;

  • Move the Ideal Location closer to the triangle plane (due to the fact, that particles forming the triangle basis may be separated from one another and in such case the fourth particle is located closer to the triangle plane);

  • Find the particle nearest to the Ideal Location—this is the Real Location (RL) of the 4th particle forming tetrahedron in the space;

  • Remove the lowest sphere from tetrahedron 1–4 to obtain the base triangle for the next tetrahedron;

  • Calculate the local length of the path inside the current tetrahedron (a local path is the line connecting centroids of base triangles of two neighbouring tetrahedrons);

  • Continue the calculations, until reaching the top surface of the bed.

The algorithm stops when the distance between the gravity centre and the Ideal Location is smaller than the distance between the top surface of the bed and the Z coordinate of the Ideal Location. The last section is perpendicular to the top surface of the bed. The final path length \(L_p^g\) is calculated as the sum of all local path lengths inside tetrahedrons and two sections lying at the beginning as well as at the end of the analyzed pore channel.

2.3 Standard method

In the Standard Method (SM) 25 ISPs located on the bottom surface of the bed are always chosen and the paths lengths from these points are then obtained. These localizations are visible in Fig. 3. The description of the point location contains two signs: the first refers to the X axis, the second to the Y axis. Both signs can have values of “−” (the negative part of the axis), “0” (zero point of the axis) and “\(+\)” (the positive part of the axis). The combination of signs is as follows: \(+0\), \(+-\), \(0-\), −, \(-0\), \(-+\), \(0+\), \(++\), 00. To control the distance between the ISP and the centre of the coordinate system, two additional variables are used: xshift and yshift (in a cylindrical domain only the xshift is used to define the distance between the zero point and the wall). These coefficients may be between 0 (the ISP located in the zero point—the middle of the bottom domain wall) and 1 (the ISP located on the wall). In the Standard Method the default values for both coefficients equal 0.25, 0.5 and 0.75, respectively.

2.4 Regular Grid Method

In the current article a Regular Grid Method (RGM) is proposed. In this method the PTM is exactly the same as earlier, but the way of choosing the ISP is different. In this approach, both ranges of coordinates in the X and Y directions are divided into \(n_x\) and \(n_y\) points, respectively. Next, in a loop all these points are used as more ISP (Fig. 4). With this method any number of paths for one bed may be analysed. If the calculation domain is cylindrical, the ISP lying in the distance equal or further than the cylinder radius, are not taken into account. In Fig. 4 such points are grey.

Fig. 4
figure 4

Locations of the ISP in the bottom surface of the bed in the Regular Grid Method

Full size image
Fig. 5
figure 5

Visualisation of virtual beds created in the YADE code (left) and in the PFC3D code (right)

Full size image
Table 1 Main information about virtual beds
Full size table

3 Results

3.1 Virtual beds

To illustrate the action of the RGM, two virtual beds created with the use of the Discrete Element Method (DEM) are used (Fig. 5). One of them was created in the YADE code [38] and the other by Liu et al. [39, 40] in the PFC3D code [41]. In both cases the porosity was equal to 0.42. The details related to these examples the Reader can find in e.g. the paper [37], and therefore this issue is not being described in the hereby article. Main information related to both examples is collected in Table 1.

3.2 Tortuosity field

Virtual beds presented in the previous section were used for calculating the tortuosity. The PTM was used in every case, but two different approaches to choosing the IPS were applied: Standard Method (SM) and Regular Grid Method (RGM).

In Fig. 6 the values of tortuosity obtained for different ISP’s, the SM and the YADE example are visible. The ISP were chosen according to Fig. 3 (left). The average value of tortuosity (from 25 paths) is equal to 1.226 with the minimum and maximum values equal to 1.18 (3.8 %) and 1.264 (3.1 %), respectively. The standard deviation is 0.02473. The percentages in the parentheses denote the relative errors in relation to the average value. In the SM only the average or extreme values of the tortuosity may be calculated. It is impossible to conclude anything about the tortuosity distribution or about the volatility of this parameter in the space. More data are needed for such investigations. In this case the average calculation time of one path was equal to 1.51 [s]. This time depends in general on the used computer (here a typical modern notebook was applied), Operating System (here it was MS Windows 7), as well as on the settings of the PathFinder code (these settings were constant in all calculations shown in the paper).

Fig. 6
figure 6

Results of calculations in the Standard Method for the YADE example

Full size image

In Fig. 7, the results of applying the RGM for the same virtual bed are shown—this time in form of a 2D function. X and Y means coordinates of Initial Starting Points. On the Z axis in turn, the values of tortuosity are shown. They are obtained for paths starting from all these points. The size of the ISP grid (see Fig. 4) is in this case equal to 10,000 (where \(n_x=n_y=100\)). The computation time (about 10.5 h) is much longer than the previous one, but the number of tortuosity values is incomparably higher and gives new possibilities. The average value of tortuosity is the same (1.226), but the minimum and maximum values are more protruding: 1.153 (6 %) and 1.339 (9.2 %), respectively. The standard deviation in this case is equal to 0.03656. A wider range of the results was expected, due to the fact that the space was densely searched.

Fig. 7
figure 7

Results of calculations in the Regular Grid Method for the YADE example (note that x and y axis are not in the same scale)

Full size image

Analysing Fig. 7 it may by seen that the tortuosity value does not change suddenly, but in some zones it is higher while in others it is lower. It is caused by the fact that the space step in the RGM is less significant than the minimum particle diameter. For example, the domain size in the X direction is equal to 0.9019 [m]. In this direction 100 ISP exist, thus the space step is equal to 8.93 [mm]. This value is few times lower than the minimum particle diameter (31.1 [mm]). As a consequence in many cases the path has to lead through the same pore channels: in the entire length of the path or in a section. Such a case was registered for the RM and the paths denoted by “\(-+\)” and “\(-0\)” (Fig. 8). It can be assumed that this phenomenon will be more frequent, if the space step is decreased. Hence, the adjacent paths lead partly through the same pore channels and the lengths of many neighbouring paths are similar.

Fig. 8
figure 8

An example of paths leading partially in the same pore channel

Full size image
Fig. 9
figure 9

Results of calculations in the Regular Grid Method for the PFC3D example (note that x and y axis are not in the same scale)

Full size image
Table 2 Results of statistical analysis
Full size table
Fig. 10
figure 10

Histograms of the tortuosity for the YADE (left) and the PFC3D example (right)

Full size image

The tortuosity field for the second example is shown in Fig. 9. This time the tortuosity field is circular, which stems from a cylindrical shape of the virtual bed. The average, minimum and maximum values from the RGM are as follows: 1.232, 1.163 (5.6 %) and 1.312 (6.5 %). The same numbers for the SM are 1.241, 1.199 (3.4 %) and 1.286 (3.6 %), respectively. The standard deviation equals as follow: 0.02594 for SM and 0.02672 for the RGM approach. The main difference is that the average values differ slightly (with the relative error between both average values \({<}0.8\,\%\)). The conclusion is that the minimum number of paths, which can be a good representation of the tortuosity for the whole bed, should be increased with the growth of the number of particles in the bed. The average calculation times of one path was in this example equal to 3.75 [s]. The total time of calculation with the use of the RGM is in the order of 10 h. It is still much less if compared to the resolution time of balance equations in VOF or probability density function in the LBM methods. It should also take into account the fact, that the computational grid needed for mentioned methods will be probably too big for the average computer (the bed in this case consist of 18,188 particles).

It can be added that the average values obtained in the SM or the RGM are different from the values shown in the article [37]. The reason is that only individual values were shown there (for a path starting from the ’00’ ISP).

In Table 2 the results of the statistical analysis performed in the R [42] environment for both examples of the Regular Grid Method are collected. It can be concluded that both distributions are not normal (five different normality tests were made) and are leptokurtic. It is interesting that in the PFC3D example the tortuosity histogram (Fig. 10) is more symmetric than in the YADE case. Perhaps the PFC3D example is more representative due to the higher number of particles in the bed. The other possibility is that there are different correlations between the particle size, the particle distribution, the bed porosity and the distributions of the tortuosity. This issue is open and may be a motivation for further investigations.

4 Summary

The following conclusions can be formulated on the basis of the above discussed topics:

  • The Path Tracking Method may be applied in different ways. For the same data, one, several or thousands different paths may be obtained.

  • The Regular Grid Method allows to obtain thousands of values of tortuosity. Such data may be helpful in analysing the tortuosity distribution in a granular bed or in analysing the variability of this parameter in the space. Such conclusions point at interesting directions of future investigations.

  • It was stated on the basis of a statistical analysis that the obtained tortuosity distribution curves are not normal.

  • The obtained results suggest that the minimum number of the grid points in the RGM should be adapted to the bed size and the minimum particle diameter. The space step in the current direction should be less than this minimum diameter.

  • By the use of the RGM, the coordinates of places, from which the shortest and the longest paths begin in the bed, may be obtained.

  • The Standard Method seems to be sufficient if only the average value of the tortuosity is needed. This conclusion is in agreement with the earlier investigations, described in the paper [32].

  • It can be assumed that the relative error between average values obtained with the use of the SM and the RGM increases if the number of particles grows.