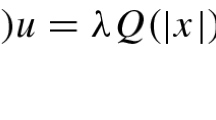Abstract
We investigate nonlinear Schrödinger–Poisson systems in the 3-sphere. We prove existence results for these systems and discuss the question of the stability of the systems with respect to their phases. While, in the subcritical case, we prove that all phases are stable, we prove in the critical case that there exists a sharp explicit threshold below which all phases are stable and above which resonant frequencies and multi-spikes blowing-up solutions can be constructed. Solutions of the Schrödinger–Poisson systems are standing waves solutions of the electrostatic Maxwell–Schrödinger system. Stable phases imply the existence of a priori bounds on the amplitudes of standing waves solutions. Unstable phases give rise to resonant states.
Similar content being viewed by others
References
Ambrosetti, A., Malchiodi, A.: Perturbation methods and semilinear elliptic problems in R n. In: Progress in Mathematics, vol. 240. Birkhauser Verlag, Basel (2006)
Bahri, A.: Critical Points at Infinity in Some Variational Problems. Pitman Research Notes in Mathematics Series, vol. 182. Longman Scientific & Technical, Harlow; copublished in the United States with Wiley, Inc., New York (1989)
Bianchi G., Egnell H.: A note on the Sobolev inequality. J. Funct. Anal. 100, 18–24 (1991)
Brézis H., Nirenberg L.: Positive solutions of nonlinear ellitpic equations involving critical Sobolev exponents. Commun. Pure Appl. Math. 36, 437–477 (1983)
Caffarelli L.A., Gidas B., Spruck J.: Asymptotic symmetry and local behavior of semilinear elliptic equations with critical Sobolev growth. Commun. Pure Appl. Math. 42, 271–297 (1989)
Chen C.C., Lin C.S.: Estimates of the conformal scalar curvature equation via the method of moving planes. Commun. Pure Appl. Math. 50, 971–1017 (1997)
Del Pino M., Felmer P., Musso M.: Two-bubble solutions in the super-critical Bahri–Coron’s problem. Calc. Var. Partial Differ. Equ. 16, 113–145 (2003)
Druet O., Hebey E.: Stability for strongly coupled critical elliptic systems in a fully inhomogeneous medium. Anal. PDEs 2, 305–359 (2009)
Druet O., Hebey E.: Existence and a priori bounds for electrostatic Klein–Gordon–Maxwell systems in fully inhomogeneous spaces. Commun. Contemp. Math. 12, 831–869 (2010)
Druet O., Laurain P.: Stability of the Pohozaev obstruction in dimension 3. J. Eur. Math. Soc. 12, 1117–1149 (2010)
Druet, O., Hebey, E., Robert, F.: Blow-Up Theory for Elliptic PDEs in Riemannian Geometry Mathematical Notes, vol. 45. Princeton University Press, Princeton, NJ (2004)
Druet O., Hebey E., Vétois, J.: Bounded stability for strongly coupled critical elliptic systems below the geometric threshold of the conformal Laplacian. J. Funct. Anal. 258, 999–1059 (2010)
Gidas B., Spruck J.: A priori bounds for positive solutions of nonlinear elliptic equations. Commun. Partial. Differ. Equ. 6, 883–901 (1981)
Goldhaber A.S., Nieto M.M.: Terrestrial and extraterrestrial limits on the photon mass. Rev. Mod. Phys. 43, 277–296 (1971)
Goldhaber A.S., Nieto M.M.: Photon and graviton mass limits. Rev. Mod. Phys. 82, 939–979 (2010)
Hebey E., Robert F.: Asymptotic analysis for fourth order Paneitz equations with critical growth. Adv. Calc. Var. 4, 229–275 (2011)
Hebey, E., Truong, T.T.: Static Klein–Gordon–Maxwell–Proca systems in 4-dimensional closed manifolds. J. Reine Angew. Math. (to appear)
Hebey E., Robert F., Wen Y.: Compactness and global estimates for a fourth order equation of critical Sobolev growth arising from conformal geometry. Commun. Contemp. Math. 8, 9–65 (2006)
Li Y.Y., Zhang L.: A Harnack type inequality for the Yamabe equations in low dimensions. Calc. Var. Partial Differ. Equ. 20, 133–151 (2004)
Luo J., Gillies G.T., Tu L.C.: The mass of the photon. Rep. Prog. Phys. 68, 77–130 (2005)
Pauli W.: Relativistic field theories of elementary particles. Rev. Mod. Phys. 13, 203–232 (1941)
Rey O., Wei J.: Blowing up solutions for an elliptic Neumann problem with sub- or supercritical nonlinearity. I. N = 3. J. Funct. Anal. 212, 472–499 (2004)
Robert, F.: Green’s functions estimates for elliptic type operators. Preprint (2006)
Ruegg H., Ruiz-Altaba M.: The Stueckelberg field. Int. J. Mod. Phys. A 19, 3265–3348 (2004)
Schrödinger E.: The Earth’s and the Sun’s permanent magnetic fields in the unitary field theory. Proc. R. Ir. Acad. A 49, 135–148 (1943)
Struwe M.: A global compactness result for elliptic boundary problems involving limiting nonlinearities. Math. Z. 187, 511–517 (1984)
Wei, J.: Existence and stability of spikes for the Gierer-Meinhardt system. In: Handbook of Differential Equations: Stationary Partial Differential Equations vol. V, pp. 487–585. Elsevier/North-Holland, Amsterdam (2008)
Willem, M.: Minimax theorems. In: Progress in Nonlinear Differential Equations and Their Applications, vol. 24. Birkhäuser Boston, Inc., Boston, MA (1996)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by A. Malchiodi.