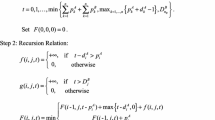Abstract
This paper considers a two-agent scheduling problem with arbitrary release dates on a single machine. The cost of the first agent is the maximum weighted completion time of its jobs while the cost of the second agent is the total weighted completion time of its jobs. The goal is to schedule the jobs such that the total cost of the two agents is minimized. The problem is known to be strongly NP-hard. Thus, as an alternative, a branch-and-bound algorithm incorporating several dominance properties and a lower bound is provided to derive the optimal solution and a largest- order-value method combined with proposed three initials is developed to derive the near-optimal solutions for the problem. Computational results are also presented to evaluate the performance of the proposed algorithms.












Similar content being viewed by others
References
Agnetis A, Mirchandani PB, Pacciarelli D, Pacifici A (2004) Scheduling problems with two competing agents. Oper Res 52:229–242
Agnetis A, Pacciarelli D, Pacifici A (2007) Multi-agent single machine scheduling. Ann Oper Res 150:3–15
Agnetis A, Billaut J-C, Gawiejnovicz S, Pacciarelli D, Soukhal A (2014) Multiagent scheduling. Models and algorithms. Springer, Berlin
Baker KR, Smith JC (2003) A multiple-criterion model for machine scheduling. J Sched 6:7–16
Bean JC (1994) Genetic algorithms and random keys for sequencing and optimization. ORSA J Comput 6:154–160
Belouadah H, Posner ME, Potts CN (1992) Scheduling with release dates on a single machine to minimize total weighted completion time. Discrete Appl Math 36:213–231
Behnamian J, Fatemi Ghomi SMT (2014) Multi-objective fuzzy multiprocessor flowshop scheduling. Appl Soft Comput 21:139–148
Cheng SR (2012) A single-machine two-agent scheduling problem by GA approach. Asia-Pac J Oper Res 29(2):1250013
Cheng TCE, Ng CT, Yuan JJ (2006) Multi-agent scheduling on a single machine to minimize total weighted number of tardy jobs. Theor Comput Sci 362:273–281
Cheng TCE, Ng CT, Yuan JJ (2008) Multi-agent scheduling on a single machine with max-form criteria. Eur J Oper Res 188:603–609
Cheng TCE, Cheng SR, Wu WH, Hsu PH, Wu CC (2011a) A two-agent single-machine scheduling problem with truncated sum-of-processing-times-based learning considerations. Comput Ind Eng 60:534–541
Cheng TCE, Wu WH, Cheng SR, Wu CC (2011b) Two-agent scheduling with position-based deteriorating jobs and learning effects. Appl Math Comput 217:8804–8824
Cheng TCE, Wu C-C, Chen J-C, Wu W-H, Cheng S-R (2013) Two-machine owshop scheduling with a truncated learning function to minimize the makespan. Int J Prod Econ 141:79–86
Dessouky MM (1998) Scheduling identical jobs with unequal ready times on uniform parallel machines to minimize the maximum lateness. Comput Ind Eng 34(4):793–806
Elvikis D, Kindt VT (2014) Two-agent scheduling on uniform parallel machines with min-max criteria. Ann Oper Res 213(1):79–94
Feng Q, Yuan JJ (2007) NP-hardness of a multicriteria scheduling on two families of jobs. OR Trans 11(4):121–126
Gerstl E, Mosheiov G (2013) Scheduling problems with two competing agents to minimized weighted earliness-tardiness. Comput Oper Res 40:109–116
Gerstl E, Mosheiov G (2014) Single machine just-in-time scheduling problems with two competing agents. Naval Res Logist 61:1–16
Han S, Peng Z, Wang S (2014) The maximum flow problem of uncertain network. Inf Sci 265:167–175
Ke H, Ma J (2014) Modeling project time-cost trade-off in fuzzy random environment. Appl Soft Comput 19:80–85
Lee K, Choi BC, Leung JYT, Pinedo ML (2009) Approximation algorithms for multi-agent scheduling to minimize total weighted completion time. Inf Process Lett 109:913–917
Lee WC, Chen SK, Wu CC (2010) Branch-and-bound and simulated annealing algorithms for a two-agent scheduling problem. Expert Syst Appl 37:6594–6601
Lee WC, Chen SK, Chen WC, Wu CC (2011) A two-machine flowshop problem with two agents. Comput Oper Res 38:98–104
Leung JYT, Pinedo M, Wan G (2010) Competitive two-agent scheduling and its applications. Oper Res 58:458–469
Liu G, Zeng Y, Li D, Chen Y (2014) Schedule length and reliability-oriented multi- objective scheduling for distributed computing. Soft Comput. doi:10.1007/s00500-014-1360-3
Luo W, Chen L, Zhang G (2012) Approximation schemes for two-machine flow shop scheduling with two agents. J Comb Optim 24(3):229–239
Mor B, Mosheiov G (2010) Scheduling problems with two competing agents to minimize minmax and minsum earliness measures. Eur J Oper Res 206:540–546
Marichelvam MK, Prabaharan T, Yang XS (2014) Improved cuckoo search algorithm for hybrid flow shop scheduling problems to minimize makespan. Appl Soft Comput 19:93–101
Ng CT, Cheng TCE, Yuan JJ (2006) A note on the complexity of the problem of two-agent scheduling on a single machine. J Comb Optim 12:387–394
Nong QQ, Cheng TCE, Ng CT (2011) Two-agent scheduling to minimize the total cost. Eur J Oper Res 215:39–44
Ou Z-H, Chen L-H (2014) A steganographic method based on tetris games. Inf Sci 276:343–353
Reeves C (1995) Heuristics for scheduling a single machine subject to unequal job release times. Eur J Oper Res 80:397–403
Storn R, Price K (1997) Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces. J Glob Optim 11(4):341–359
Tamura Y, Iizuka H, Yamamoto M, Furukawa M (2015) Application of local clustering organization to reactive job-shop scheduling. Soft Comput 29(4):891–899
Wan G, Vakati RS, Leung JYT, Pinedo M (2010) Scheduling two agents with controllable processing times. Eur J Oper Res 205:528–539
Wu W-H, Cheng S-R, Wu C-C, Yin Y (2012) Ant colony algorithms for two-agent scheduling with sum-of-processing-times-based learning and deteriorating considerations. J Intell Manuf 23:1985–1993
Wu C-C, Wu W-H, Chen J-C, Yin Y, Wu W-H (2013) A study of the single-machine two-agent scheduling problem with release times. Appl Soft Comput 13(2):998–1002
Wu W-H, Yin Y, Wu W-H, Wu C-C, Hsu P-H (2014a) A time-dependent scheduling problem to minimize the sum of the total weighted tardiness among two agents. J Ind Manag Optim 10(2):591–611
Wu C-C, Wu W-H, Wu W-H, Hsu P-H, Yin Y, Xu J (2014b) A single-machine scheduling with a truncated linear deterioration and ready times. Inf Sci 256:109–125
Yin Y, Cheng S-R, Cheng TCE, Wu C-C, Wu W-H (2012a) Two-agent single-machine scheduling with assignable due dates. Appl Math Comput 219:1674–1685
Yin Y, Wu W-H, Cheng S-R, Wu C-C (2012b) An investigation on a two-agent single-machine scheduling problem with unequal release dates. Comput Oper Res 39:3062–3073
Yin Y, Cheng S-R, Wu C-C (2012c) Scheduling problems with two agents and a linear non-increasing deterioration to minimize earliness penalties. Inf Sci 189:282–292
Yin Y, Cheng S-R, Cheng TCE, Wu W-H, Wu C-C (2013a) Two-agent single-machine scheduling with release times and deadlines. Int J Shipp Transport Logist 5(1):75–94
Yin Y, Wu C-C, Wu W-H, Hsu C-J, Wu W-H (2013b) A branch-and-bound procedure for a single-machine earliness scheduling problem with two agents. Appl Soft Comput 13:1042–1054
Yin Y, Wu W-H, Wu W-H, Wu C-C (2014) A branch-and-bound algorithm for a single machine sequencing to minimize the total tardiness with arbitrary release dates and position-dependent learning effects. Inf Sci 256:91–108
Acknowledgments
We thank the Editor, an Associate Editor, and two anonymous referees for their helpful comments on the earlier version of our paper. This paper was supported in part by the National Natural Science Foundation of China (71301022); in part by the Personnel Training Fund of Kunming University of Science and Technology under Grant Number KKSY201407098; and in part by the Ministry of Science Technology (MOST) of Taiwan under Grant No. NSC 102-2221-E-035-070-MY3, Grant No. MOST 103-2410-H-035-022-MY2, and Grant No. NSC 102-2410-H-264-003.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by V. Loia.
Rights and permissions
About this article
Cite this article
Wang, DJ., Yin, Y., Wu, WH. et al. A two-agent single-machine scheduling problem to minimize the total cost with release dates. Soft Comput 21, 805–816 (2017). https://doi.org/10.1007/s00500-015-1817-z
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-015-1817-z