Skip to main content
SpringerLink
Log in

Quadratic solid–shell elements for nonlinear structural analysis and sheet metal forming simulation

  • Original Paper
  • Published:
Computational Mechanics Aims and scope Submit manuscript

Abstract

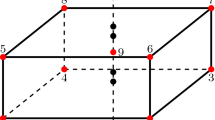
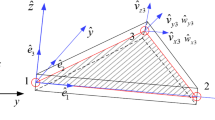
In this paper, two quadratic solid–shell (SHB) elements are proposed for the three-dimensional modeling of thin structures. These consist of a 20-node hexahedral solid–shell element, denoted SHB20, and its 15-node prismatic counterpart, denoted SHB15. The formulation of these elements is extended in this work to include geometric and material nonlinearities, for application to problems involving large displacements and rotations as well as plasticity. For this purpose, the SHB elements are coupled with large-strain anisotropic elasto-plastic constitutive equations for metallic materials. Although based on a purely three-dimensional approach, several modifications are introduced in the formulation of these elements to provide them with interesting shell features. In particular, a special direction is chosen to represent the thickness, along which a user-defined number of integration points are located. Furthermore, for efficiency requirements and for alleviating locking phenomena, an in-plane reduced-integration scheme is adopted. The resulting formulations are implemented into the finite element software ABAQUS/Standard and, to assess their performance, a variety of nonlinear benchmark problems are investigated. Attention is then focused on the simulation of various complex sheet metal forming processes, involving large strain, anisotropic plasticity, and double-sided contact. From all simulation results, it appears that the SHB elements represent an interesting alternative to traditional shell and solid elements, due to their versatility and capability of accurately modeling selective nonlinear benchmark problems as well as complex sheet metal forming processes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28
Fig. 29
Fig. 30
Fig. 31
Fig. 32
Fig. 33
Fig. 34
Fig. 35
Fig. 36
Fig. 37
Fig. 38

Similar content being viewed by others

References

  1. Zienkiewicz OC, Taylor RL, Too JM (1971) Reduced integration technique in general analysis of plates and shells. Int J Numer Methods Eng 3:275–290

    Article  MATH  Google Scholar 

  2. Cho C, Park HC, Lee SW (1998) Stability analysis using a geometrically nonlinear assumed strain solid shell element model. Finite Elem Anal Des 29:121–135

    Article  MATH  Google Scholar 

  3. Hauptmann R, Schweizerhof K (1998) A systematic development of ‘solid-shell’ element formulations for linear and non-linear analyses employing only displacement degrees of freedom. Int J Numer Methods Eng 42:49–69

    Article  MATH  Google Scholar 

  4. Puso MA (2000) A highly efficient enhanced assumed strain physically stabilized hexahedral element. Int J Numer Methods Eng 49:1029–1064

  5. Sze KY, Yao LQ (2000) A hybrid stress ANS solid-shell element and its generalization for smart structure modelling, part I—-solid–shell element formulation. Int J Numer Methods Eng 48:545–564

  6. Abed-Meraim F, Combescure A (2002) SHB8PS—a new adaptive, assumed-strain continuum mechanics shell element for impact analysis. Comput Struct 80:791–803

    Article  Google Scholar 

  7. Kim JH, Kim YH (2002) A three-node \(\text{ C }^{0}\) ANS element for geometrically non-linear structural analysis. Comput Methods Appl Mech Eng 191:4035–4059

    Article  MATH  Google Scholar 

  8. Alves de Sousa RJ, Cardoso RPR, Fontes Valente RA, Yoon JW, Grácio JJ, Natal Jorge RM (2005) A new one-point quadrature enhanced assumed strain (EAS) solid–shell element with multiple integration points along thickness: part I—geometrically linear applications. Int J Numer Methods Eng 62:952–977

    Article  MATH  Google Scholar 

  9. Parente MPL, Fontes Valente RA, Natal Jorge RM, Cardoso RPR, Alves de Sousa RJ (2006) Sheet metal forming simulation using EAS solid–shell finite elements. Finite Elem Anal Des 42:1137–1149

    Article  Google Scholar 

  10. Reese S (2007) A large deformation solid–shell concept based on reduced integration with hourglass stabilization. Int J Numer Methods Eng 69:1671–1716

    Article  MathSciNet  MATH  Google Scholar 

  11. Cardoso RPR, Yoon JW, Mahardika M, Choudhry S, Alves de Sousa RJ, Fontes Valente RA (2008) Enhanced assumed strain (EAS) and assumed natural strain (ANS) methods for one-point quadrature solid–shell elements. Int J Numer Methods Eng 75:156–187

    Article  MathSciNet  MATH  Google Scholar 

  12. Abed-Meraim F, Combescure A (2009) An improved assumed strain solid-shell element formulation with physical stabilization for geometric non-linear applications and elastic–plastic stability analysis. Int J Numer Methods Eng 80:1640–1686

    Article  MathSciNet  MATH  Google Scholar 

  13. Schwarze M, Reese S (2009) A reduced integration solid–shell finite element based on the EAS and the ANS concept—geometrically linear problems. Int J Numer Methods Eng 80:1322–1355

    Article  MathSciNet  MATH  Google Scholar 

  14. Li LM, Peng YH, Li DY (2011) A stabilized underintegrated enhanced assumed strain solid–shell element for geometrically nonlinear plate/shell analysis. Finite Elem Anal Des 47:511–518

    Article  Google Scholar 

  15. Edem IB, Gosling PD (2012) One-point quadrature ANS solid–shell element based on a displacement variational formulation, part I–geometrically linear assessment. Comput Methods Appl Mech Eng 237–240:177–191

    Article  MathSciNet  MATH  Google Scholar 

  16. Flores FG (2013) Development of a non-linear triangular prism solid–shell element using ANS and EAS techniques. Comput Methods Appl Mech Eng 266:81–97

    Article  MathSciNet  MATH  Google Scholar 

  17. Pagani M, Reese S, Perego U (2014) Computationally efficient explicit nonlinear analyses using reduced integration-based solid–shell finite elements. Comput Methods Appl Mech Eng 268:141–159

    Article  MathSciNet  MATH  Google Scholar 

  18. Schwarze M, Vladimirov IN, Reese S (2011) Sheet metal forming and springback simulation by means of a new reduced integration solid–shell finite element technology. Comput Methods Appl Mech Eng 200:454–476

    Article  MATH  Google Scholar 

  19. Salahouelhadj A, Abed-Meraim F, Chalal H, Balan T (2012) Application of the continuum shell finite element SHB8PS to sheet forming simulation using an extended large strain anisotropic elastic-plastic formulation. Arch Appl Mech 82:1269–1290

  20. Trinh VD, Abed-Meraim F, Combescure A (2011) A new assumed strain solid–shell formulation “SHB6” for the six-node prismatic finite element. J Mech Sci Technol 25:2345–2364

    Article  Google Scholar 

  21. Abed-Meraim F, Trinh VD, Combescure A (2013) New quadratic solid–shell elements and their evaluation on linear benchmark problems. Computing 95:373–394

    Article  MathSciNet  MATH  Google Scholar 

  22. Zienkiewicz OC, Taylor RL, Zhu JZ (2006) The finite element method, 6th edn. Elsevier, Amsterdam

    Google Scholar 

  23. Hallquist JO (1983) Theoretical manual for DYNA3D. Report UC1D-19041, Lawrence Livermore National Laboratory, Livermore

  24. Simo JC, Hughes TJR (1986) On the variation foundations of assumed strain methods. J Appl Mech 53:51–54

    Article  MathSciNet  MATH  Google Scholar 

  25. Hill R (1948) A theory of the yielding and plastic flow of anisotropic metals. Proc R Soc Lond A 193:281–297

    Article  MathSciNet  MATH  Google Scholar 

  26. Timoshenko S, Woinowsky-Krieger S (1959) Theory of plates and shells, 2nd edn. McGraw-Hill, New York

    MATH  Google Scholar 

  27. Peng X, Crisfield M (1992) A consistent co-rotational formulation for shells using the constant stress/constant moment triangle. Int J Numer Methods Eng 35:1829–1847

    Article  MATH  Google Scholar 

  28. Sansour C, Bufler H (1992) An exact finite rotation shell theory, its mixed variational formulation and its finite element implementation. Int J Numer Methods Eng 34:73–115

    Article  MathSciNet  MATH  Google Scholar 

  29. Sze KY, Liu XH, Lo SH (2004) Popular benchmark problems for geometric nonlinear analysis of shells. Finite Elem Anal Des 40:1551–1569

    Article  Google Scholar 

  30. Park HC, Cho C, Lee SW (1995) An efficient assumed strain element model with 6 dof per node for geometrically nonlinear shells. Int J Numer Methods Eng 38:4101–4122

    Article  MATH  Google Scholar 

  31. Sze KY, Chan WK, Pian THH (2002) An eight-node hybrid-stress solid–shell element for geometric non-linear analysis of elastic shells. Int J Numer Methods Eng 55:853–878

    Article  MATH  Google Scholar 

  32. Hsiao KM (1987) Nonlinear analysis of general shell structures by flat triangular elements. Comput Struct 25:665–675

    Article  MATH  Google Scholar 

  33. Barut A, Madenci E, Tesslerb A (1997) Nonlinear analysis of laminates through a Mindlin-type shear deformable shallow shell element. Comput Methods Appl Mech Eng 143:155–173

    Article  MATH  Google Scholar 

  34. Smoleński WM (1999) Statically and kinematically exact nonlinear theory of rods and its numerical verification. Comput Methods Appl Mech Eng 178:89–113

    Article  MathSciNet  MATH  Google Scholar 

  35. Mostafa M, Sivaselvan MV, Felippa CA (2013) A solid-shell corotational element based on ANDES, ANS and EAS for geometrically nonlinear structural analysis. Int J Numer Methods Eng 95:145–180

    Article  MathSciNet  MATH  Google Scholar 

  36. Betsch P, Stein E (1999) Numerical implementation of multiplicative elasto-plasticity into assumed strain elements with application to shells at large strains. Comput Methods Appl Mech Eng 179:215–245

    Article  MathSciNet  MATH  Google Scholar 

  37. Fontes Valente RA, Alves de Sousa RJ, Natal Jorge RM (2004) An enhanced strain 3D element for large deformation elastoplastic thin-shell applications. Comput Mech 34:38–52

    MATH  Google Scholar 

  38. Cardoso RPR, Yoon JW (2005) One point quadrature shell element with through-thickness stretch. Comput Methods Appl Mech Eng 194:1161–1199

    Article  MATH  Google Scholar 

  39. Wriggers P, Eberlein R, Reese S (1996) A comparison of three-dimensional continuum and shell elements for finite plasticity. Int J Solids Struct 33:3309–3326

    Article  MATH  Google Scholar 

  40. Eberlein R, Wriggers P (1999) Finite element concepts for finite elastoplastic strains and isotropic stress response in shells: theoretical and computational analysis. Comput Methods Appl Mech Eng 171:243–279

    Article  MATH  Google Scholar 

  41. Hauptmann R, Schweizerhof K, Doll S (2000) Extension of the ‘solid-shell’ concept for application to large elastic and large elastoplastic deformations. Int J Numer Methods Eng 49:1121–1141

    Article  MATH  Google Scholar 

  42. Makinouchi A, Nakamachi E, Oñate E, Wagoner RH (1993) NUMISHEET’93, Proceedings of the 2nd international conference and workshop on numerical simulation of 3D sheet metal forming processes—verification of simulation with experiment, Isehara

  43. Park DW, Oh SI (2004) A four-node shell element with enhanced bending performance for springback analysis. Comput Methods Appl Mech Eng 193:2105–2138

    Article  MATH  Google Scholar 

  44. Zhang DJ, Cui ZS, Ruan XY, Li YQ (2007) An analytical model for predicting springback and side wall curl of sheet after U-bending. Comput Mater Sci 38:707–715

    Article  Google Scholar 

  45. Dvorkin EN, Bathe KJ (1984) A continuum mechanics based four-node shell element for general nonlinear analysis. Eng Comput 1:77–88

    Article  Google Scholar 

  46. Bouffioux C, Eyckens P, Henrard C, Aerens R, Van Bael A, Sol H, Duflou JR, Habraken AM (2008) Identification of material parameters to predict Single Point Incremental Forming forces. Int J Plasticity 1:1147–1150

    Google Scholar 

  47. Sena JIV, Alves de Sousa RJ, Valente RAF (2010) Single point incremental forming simulation with an enhanced assumed strain solid–shell finite element formulation. Int J Mater Form 3:963–966

    Article  Google Scholar 

  48. Wriggers P (2006) Computational contact mechanics, 2nd edn. Springer, Berlin

    Book  MATH  Google Scholar 

  49. Xu HJ, Liu YQ, Zhong W (2012) Three-dimensional finite element simulation of medium thick plate metal forming and springback. Finite Elem Anal Des 51:49–58

    Article  Google Scholar 

  50. Yoon JW, Barlat F, Chung K, Pourboghrat F, Yang DY (2000) Earing predictions based on asymmetric nonquadratic yield function. Int J Plasticity 16:1075–1104

  51. Yoon JW, Barlat F, Dick RE, Chung K, Kang TJ (2004) Plane stress yield function for aluminum alloy sheets, part II: FE formulation and its implementation. Int J Plasticity 20:495–522

    Article  MATH  Google Scholar 

  52. Yoon JW, Barlat F, Dick RE, Karabin ME (2006) Prediction of six or eight ears in a drawn cup based on a new anisotropic yield function. Int J Plasticity 22:174–193

    Article  MATH  Google Scholar 

  53. Schwarze M, Vladimirov IN, Reese S (2010) A new continuum shell finite element for sheet metal forming applications. Int J Mater Form 3:919–922

    Article  Google Scholar 

  54. Barlat F, Lege DJ, Brem JC (1991) A six-component yield function for anisotropic materials. Int J Plasticity 7:693–712

    Article  Google Scholar 

  55. Barlat F, Brem JC, Yoon JW, Chung K, Dick RE, Lege DJ, Pourboghrat F, Choi SH, Chu E (2003) Plane stress yield function for aluminum alloy sheets—part 1: theory. Int J Plasticity 19:1297–1319

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. LEM3, UMR CNRS 7239 - Arts et Métiers ParisTech, 4, rue Augustin Fresnel, 57078, Metz Cedex 03, France

    Peng Wang, Hocine Chalal & Farid Abed-Meraim

Authors
  1. Peng Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hocine Chalal
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Farid Abed-Meraim
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Farid Abed-Meraim.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, P., Chalal, H. & Abed-Meraim, F. Quadratic solid–shell elements for nonlinear structural analysis and sheet metal forming simulation. Comput Mech 59, 161–186 (2017). https://doi.org/10.1007/s00466-016-1341-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00466-016-1341-8

Keywords

Search

Navigation