1 Introduction

It is currently estimated that even 90% of technological problems accompanying the casting production are related to not proper proceedings of a mold pouring. During this process liquid metal flows via the gating system channels into the mold cavity (Fig. 1). In case of the majority of casting technologies (apart from the vacuum casting) when the pouring starts the mold is filled with the air. The air as well as other gases, formed due to the thermal degradation of molding materials [1, 2], are compressed by the flowing stream and ‘pushed out’ from the mold via pores in its structure (sand molds) and special venting elements, open feeders etc. Simultaneously, not proper or not efficient enough venting system can cause that gases will constitute a barrier, not allowing the casting alloy to fill completely the mold cavity [3]. In case when the liquid metal motion is accompanied with turbulences, gas bubbles can be also enclosed within the stream which, in consequence, leads to casting defects difficult to be removed [4, 5].

Fig. 1
figure 1

Schematic presentation of the mold filling process: (a) casting system, (b) empty (filled with air) mold before pouring, (c) metal flow in gating system, (d) filling the mold cavity together with the air evacuation process

Full size image

As can be seen, pouring of a casting mold is an example of a two-phase flow: liquid metal - gas and its character and kinetics has an essential influence on the final quality of cast elements. Due to its complexity and multitude of effects accompanying this process, engineers designing casting technologies are more and more often using the simulation software. These programs, regardless of their increasing popularity, are still characterized by a low efficiency. This is caused by the complicated CFD algorithms based on the Navier-Stokes (N-S) equation and VoF-like [6, 7] interface tracking methods, usually applied in them. An alternative for such approach can be the application of the Lattice Boltzmann method (LBM) [8,9,10] which, due to its high efficiency, simplicity and susceptibility to parallelization of calculations, has now become very popular in solving fluid dynamics and heat transfer [11,12,13,14] problems. On the other hand the Lattice Boltzmann method has an important drawback, which is its low numerical stability [15]. An additional issue constitutes the problem of two-phase flows modeling. There are many LB models for the multicomponent/multiphase flow, such as the method of Gunstensen et al. [16], Shan and Chen [17] and its modifications [18], Swift et al. free energy approach [19], entropic method by Mazloomi Moqaddam et al. [20] and even direct solution for casting processes [21]. However, most of them require storing separate sets of variables for each component/phase or individual distribution functions for velocity and interface tracking computations [22], which involves a high memory requirement. In some cases an additional computation step is also required to achieve zero diffusivity between fluids (immiscible). This, of course, prolongs the calculation time and decreases the algorithm efficiency. Also some other interesting but more complicated models with multiple distribution functions for multiphase/multicomponent flows conjugated with heat transfer exists [23, 24] Therefore, this work discusses the simplified numerical model of liquid-gas flows characterized by an adequate stability and accuracy, which will allow its application in simulations of the casting mold pouring process.

2 Lattice Boltzmann method for single phase flows

The basic dependence describing the model evolution in the LB method is the so-called lattice Boltzmann equation:

$$ {f}_i\left( x+{e}_i\Delta t, t+\Delta t\right)-{f}_i\left( x, t\right)=-\frac{1}{\tau}\left({f}_i\left( x, t\right)-{f_i}^{e q}\left( x, t\right)\right)+{F}_i $$
(1)

where f i is the particle distribution function in i direction, \( {f}_i^{eq} \) equilibrium distribution, x position, e i discrete velocity set, F i external force (e.g., gravity), t time and Δt is the time step.

Parameter τ is the relaxation time dependent directly on the fluid kinematic viscosity ν:

$$ \tau =\frac{\nu^{\ast }}{c_s^2}+0.5 $$
(2)

where c s is a speed of sound in the model. Index „*” concerns dimensionless values, thus

$$ {\nu}^{\ast }=\nu \frac{\Delta t}{\Delta {x}^2}. $$
(3)

The remaining dimensionless parameters for the LBM can be determined in an analogous way.

The heat exchange process was intentionally omitted in the study. However, the presented below model can be easily supplemented with the possibility of simulating the casting cooling and solidification processes, by applying the thermal lattice Boltzmann method [25].

Despite that the lattice Boltzmann method describes the fluid behavior in the mesoscopic scale [9], it is possible - on the bases of the particle distribution function - to compute, essential from the point of view of the foundry technology, macroscopic quantities including velocity:

$$ {u}^{\ast }=\frac{1}{\rho^{\ast }}\sum_{i=0}^8{f}_i{e}_i $$
(4)

and density:

$$ {\rho}^{\ast }=\sum_{i=0}^8{f}_i. $$
(5)

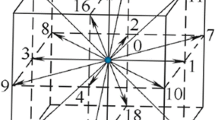
Here we used D2Q9 two-dimensional, single relaxation time (SRT) model (Fig. 2).

Fig. 2
figure 2

Discrete velocity set for a lattice cell in the D2Q9 model

Full size image

The determination of the fluid pressure p ∗ is possible by means of the equation of state:

$$ {p}^{\ast }={c}_s^2\cdot {\rho}^{\ast }. $$
(6)

On the bases of u ∗ and ρ ∗ it is possible to define the equilibrium distribution function:

$$ {f}_i^{e q}\left({\rho}^{\ast}\left( x, t\right),{u}^{\ast}\left( x, t\right)\right)={\omega}_i{\rho}^{\ast}\left[1+\frac{1}{c_s^2}\left({e}_i\cdot {u}^{\ast}\right)+\frac{1}{2{c}_s^4}{\left({e}_i\cdot {u}^{\ast}\right)}^2-\frac{1}{2{c}_s^2}{u}^{\ast 2}\right]. $$
(7)

Values of the remaining constant parameters from Eqs. (1–7) are listed in Table 1.

Table 1 Values of the selected parameters for the D2Q9 model
Full size table

3 Lattice Boltzmann method for free-surface flows

The free-surface lattice Boltzmann model developed by C. Körner for the simulation of metallic foams formation [26, 27], was used as the base for further analyses. Certain modifications of this solution and the detailed computational algorithm can be found in work [28], in which the author focused on the computer animation of the fluid motion.

In this approach all lattice cells - on the bases of the volume fraction of liquid ε l - are assigned to one of three types:

  • Type G - cells totally filled with a gaseous phase (ε l  = 0);

  • Type L - cells totally filled with a liquid phase (ε l  = 1);

  • Type I - cells filled with both phases - interface cells (ε l  ∈ (0, 1)).

Cells filled with a gaseous phase are disregarded by the numerical algorithm and thus they are determined as empty cells. Computations in the type L cells are carried out as in the lattice Boltzmann method for single-phase flows (described in section 2). The free surface tracking is done by recording fluid mass changes in interface cells.

For the interface cell, neighboring in the given direction i with the type L cell, its mass change Δm i in this direction is determined by the following equation:

$$ \Delta {m_i}^{\ast}\left( x, t+\Delta t\right)={f}_{i nv}\left( x + {e}_i\Delta t, t\right)-{f}_i\left( x, t\right) $$
(8)

where inv means the opposite direction to i.

For two neighboring interface cells the surface area, through which the mass is exchanged, should be additionally taken into account, thus:

$$ \Delta {m_i}^{\ast}\left( x, t+\Delta t\right)={s}_e\cdot \frac{\varepsilon_l\left( x+{e}_i\Delta t, t\right)+{\varepsilon}_l\left( x, t\right)}{2} $$
(9)

where

$$ {s}_e={f}_{i nv}\left( x + {e}_i\Delta t, t\right)-{f}_i\left( x, t\right). $$
(10)

The new mass value for each interface cell is computed in the following way:

$$ {m}^{\ast}\left( x, t+\Delta t\right)={m}^{\ast}\left( x, t\right)+\sum_{i=0}^8\Delta {m_i}^{\ast}\left( x, t+\Delta t\right). $$
(11)

Parameter ε l is determined on the basis of this value (ε l  = m ∗/ρ ∗) and the interface cells are converted into type L or G, respectively.

A gaseous phase is taken into consideration in this model only by the averaged pressure (density) \( {\rho}_A^{\ast } \) exerted on a free surface. Due to this, the missing particle distribution functions in Eq. (1) - streamed from the type G cells - are reconstructed with bounce-back rule:

$$ {f}_i\left( x, t+\Delta t\right)={f}_i^{eq}\left({\rho}_A^{\ast },{u}^{\ast}\left( x, t\right)\right)+{f}_{i nv}^{eq}\left({\rho}_A,{u}^{\ast}\left( x, t\right)\right)-{f}_{i nv}\left( x, t\right). $$
(12)

This approach is of a high efficiency due to neglecting type G cells in computations. In case of simple problems there is even the possibility of performing the real time simulations [29]. On the other hand, the presented model of free-surface flows is still a single-phase solution which does not allow simulations of the mentioned effects, having the influence on the castings quality. Thus, it is necessary to expand this model in such way as it would be able to take into account flows of both fluids filling the casting mold, at simultaneous retaining the high efficiency and simplicity of the computational algorithm.

4 Simplified approach to modeling two-phase: liquid-gas flows (piston model)

Problems of taking into account - in the model - mutual interactions between liquid metal and gases filling the mold are discussed here. In our solution these phases are considered separately. The gas flows (in G type cells) is treated now as a single phase flow with moving boundaries. Thus for the I cells the boundary constitute type G cells and vice versa. The interaction of both phases is taken into account by an application of the proper boundary conditions on the dividing them interface.

The idea of this method can be explained by a pictorial example of a piston moving in a cylinder (Fig. 3). The free surface of liquid metal acts as a piston which - when moving - is pressing and compressing the gases filling the mold. The result of this operation can be an increased pressure in the gaseous phase, which - in turn - will influence the liquid motion by pressing its free surface (piston surface) [25, 30].

Fig. 3
figure 3

Schematic presentation of the piston model

Full size image

For the proper representation of the interaction between liquid metal and gases filling the mold, the problem of taking into account eventual slips/frictions between these fluids is of a critical meaning. Due to this, the boundary condition presented in work [28] - allowing transferring of the moving obstacle (piston surface) momentum to the fluid as well as determining the degree of flow deceleration being the result of friction on the movable boundary - is adapted. For the type G cell in point x neighboring the interface cell in the direction inv the distribution functions, streamed from the liquid phase, will be determined according to the equation:

$$ \begin{array}{l}{f}_i\left( x, t+\Delta t\right)={w}_p\left({f}_{i nv}\left( x, t\right)+2{\omega}_i{\rho}_g^{\ast }3{e}_i\cdot {u}_0^{\ast}\right)+\left(1-{w}_p\right)\\ {}\kern5.5em \left({f}_r\left( x, t\right)+{w}_r\left( x, t\right)2{\omega}_i{\rho}_g^{\ast }3{e}_i\cdot \left[\left( n\cdot {u}_0^{\ast}\right) n\right]\right)\end{array} $$
(13)

where f r is the distribution function reconstructed by means of the free-slip boundary condition, \( {\rho}_g^{\ast } \) gas density, w p boundary friction coefficient, \( {u}_0^{\ast } \) liquid velocity in the interface cell, thus \( {u}_0^{\ast }={u}^{\ast}\left( x+{e}_{inv}\Delta t\right) \). Constant w r is assuming value 1, when function f r is reduced to the value corresponding with the no-slip boundary condition, and is 0 in other cases.

The parameter w p takes on values from 0 to 1, where for these extremes the free-slip and no-slip condition on the free surface is assumed, respectively. It should be emphasized that for w p  = 0, the momentum is only transferred in the normal direction n to the interface. Thus, to maintain the proper balance of forces at the interface the pressure of gases should also act in the n direction only.

In order to take into account, in the model, the influence of the pressure of gases on the liquid stream motion the gaseous phase global pressure \( {\rho}_A^{\ast } \) (Eq. (12)) should be substituted by the local pressure computed for individual type G cells neighboring the interface cells:

$$ \begin{array}{l}{f}_i\left( x, t+\Delta t\right)={f}_i^{e q}\left({\rho}_g^{\ast}\left( x+{e}_{i nv}, t\right),{u}^{\ast}\left( x, t\right)\right)+\\ {}+{f}_{i nv}^{e q}\left({\rho}_g^{\ast}\left( x+{e}_{i nv}, t\right),{u}^{\ast}\left( x, t\right)\right)-{f}_{i nv}\left( x, t\right).\end{array} $$
(14)

It should be mentioned in this place that one of the most important factors influencing the shape of the liquid- gas interfacial boundary is the surface tension. This force can be taken into account in the model as it is shown in paper [31]. However, in such case for the type I cell it is necessary to determine the local interface curvature, which requires several additional calculations. Admittedly, it is possible to find in references [32] solutions not requiring the interface curvature, but they also negatively influence the model efficiency. Due to this, the surface tension is omitted in the hereby paper, as it is often done in engineering calculations for the casting industry.

5 Boundary conditions

As it was mentioned, one of the advantages of the LBM is the possibility of direct defining the boundary conditions on the basis of the particle distribution functions. Therefore - according to bounce back rule - for no-slip boundary missing distribution functions in i -direction are obtained from

$$ {f}_i\left( x, t+\Delta t\right)={f}_{i nv}\left( x, t\right). $$
(15)

The free-slip boundary condition can be implemented as it is shown in paper [10].

For inlet and outlet boundary missing distribution functions are computed in the analogous way as in Eq. (14). In such case the equilibrium distribution functions are determined by the velocity or density (pressure) at inlet

$$ \begin{array}{l}{f}_i\left( x, t+\Delta t\right)={f}_i^{eq}\left({\rho}_{i n}^{\ast },{u}_{i n}^{\ast}\right)+\\ {}+{f}_{i n v}^{eq}\left({\rho}_{i n}^{\ast },{u}_{i n}^{\ast}\right)-{f}_{i n v}\left( x, t\right)\end{array} $$
(16)

or at outlet

$$ \begin{array}{l}{f}_i\left( x, t+\Delta t\right)={f}_i^{eq}\left({\rho}_{out}^{\ast },{u}_{out}^{\ast}\right)+\\ {}+{f}_{i nv}^{eq}\left({\rho}_{out}^{\ast },{u}_{out}^{\ast}\right)-{f}_{i nv}\left( x, t\right)\end{array} $$
(17)

where subscripts in and out mean values at inlet and outlet boundary, respectively.

6 Numerical stability

An essential drawback of the presented approach is its low numerical stability caused by large differences in the kinematic viscosity of both phases (indirectly caused also by differences in fluids density). The basic stability criteria in the LB method are: the dimensionless fluid velocity less than c s and the relaxation time comprising within the range (0.5, 2.5). Here we concentrate on the second one.

Along with the Reynolds number (Re) increase (the fluid viscosity decrease) the model stability decreases: τ → 0.5. Performing computations can be also impossible in case of small Re values, since τ →  ∞ . In the lattice Boltzmann method there is a direct connection between a time step and lattice step, which for the presented free-surface model [28] is as follows:

$$ \Delta t=\sqrt{\frac{g_c\cdot \Delta x}{\left| g\right|}}. $$
(18)

Parameter g c describing the allowable compressibility level, due to gravitational acceleration g, can be changed within a narrow range only and its value is usually individually selected for the given problem. Thus, this model can be treated as the weakly-compressible scheme for incompressible flows. It should be mentioned that due to relatively low velocities occurring during the mold pouring (except for the high pressure die casting technology) the assumption of the fluid incompressibility concerns liquid metal as well as gases in the casting mold and is here the condition limiting the model usage.

It can be noticed that the only parameter, which has an influence on the relaxation time (model stability) and which can be freely controlled - at least theoretically - is the lattice step Δx. By compiling Eqs. (2), (3) and (18) it is possible to determine the number N of lattice cells which will assure the proper τ value:

$$ N=\sqrt[3]{\frac{9.81{\left(\frac{\tau -0.5}{3{\nu}^{\ast }}\right)}^2}{0.0001}}\cdot l $$
(19)

where l is the domain linear size.

Substituting τ = 0.53 (empirically determined value allowing to perform computations) and τ = 2.5 into Eq. (19) the minimal N min and maximal N max number of cells in the given direction - warranting meeting the stability condition - is obtained, respectively.

As can be seen from Table 2, in the case of large viscosity differences of both fluids present in the casting mold (as for example in the case of air and liquid steel) finding the N value, which will warrant satisfying the stability criterion, can be impossible.

Table 2 N min and N max as a function of fluid kinematic viscosity and computational domain linear size
Full size table

This problem was solved by the application in the model the so-called Fractional Step (FS) method originally presented by Shu et al. [33]. The process of solving Eq. (1) within the given time step is - in this method - divided in two stages.

During the first stage (predictor step) Eq. (1) is solved for the predetermined relaxation time value, which warrants maintaining the model numerical stability (usually τ = 1). The a priori determination of τ parameter means, according to Eq. (2), that the fluid kinematic viscosity has also a certain, a priori determined value. This viscosity is called a “fictitious viscosity” since it does not concern directly the fluid physical property. On account of this, during the second stage (corrector step) the correction of the velocity field to the value corresponding the real viscosity is performed:

$$ \frac{\partial {u}^{\ast }}{\partial t}=\left(\nu -{\nu}_{FS}\right){\nabla}^2{u}^{\ast } $$
(20)

where ν FS is the fictitious viscosity computed on the bases of Eq. (2) for τ = 1.

Equation (20) is of a form of the well known diffusion equation and the number of effective numerical solutions of this equation exist. The real kinematic viscosity of modeled fluids was in a way ‘pulled out’ outside the lattice Boltzmann algorithm, and thus would not have any direct influence on the model stability [34]. However, the most time consuming part of computation is made still with the LBM, which allows to utilize this method advantages. It should be added, that the ν value in type I cells (in which both phases coexist) will linearly depend on the volume fractions of both fluids:

$$ \nu ={\varepsilon}_l{\nu}_l+\left(1-{\varepsilon}_l\right){\nu}_g $$
(21)

where subscripts l and g are related to the liquid and gaseous phase, respectively.

The complete algorithm consists of the following steps:

  • Step 1: Calculation (in interface cells) of the new mass value (Eq. (11));

  • Step 2: Solving (in G, L and I type cells) the lattice Boltzmann equation (Eq. (1)) for τ = 1;

  • Step 3: Reconstruction (in interface cells) of the missing distribution function streamed from G type cells (Eq. (14));

  • Step 4: Reconstruction (in gas cells) of the missing distribution function streamed from I type cells (Eq. (13));

  • Step 5: Reconstruction (in G, L and I type cells) of the remaining missing distribution function streamed from domain boundary (Eqs. (15–17));

  • Step 6: Computation (in G, L and I type cells) the new velocity and density values (Eqs. (4 and 5));

  • Step 7: Correction (in G, L and I type cells) the velocity field based on local viscosity (Eq. (21)) - numerical solution (here the explicit finite difference scheme is used) of Eq. (20);

  • Step 8: Computation (in G, L and I type cells) the new value of the equilibrium distribution function (Eq. (7));

  • Step 9: Conversion of I type cells, based on the determined mass value, and closing the interface again;

  • Step 10: Proceeding to the next time step.

7 Validation of the model

In this section the simulation results are compared with experimental data. Due to a high melting temperature of casting alloys and the problem with the flow recordings (not transparent molding materials) water was used as the model fluid in investigations. Water models are often applied for validating numerical simulations of casting problems [35]. This is related to a relatively low kinematic viscosity of water, similar to the viscosity of several casting alloys. In the case of non-isothermal flows some other model liquids are also used (e.g. glycerol) for their strong variation of viscosity (characteristic also for foundry alloys) with temperature [36].

7.1 Gas bubbles formation

In order to verify whether the model properly reproduces the gas bubbles formation process during mold filling, simulation results were compared with Kanatani et al. studies [37] presented in paper [38]. In this case, water is injected into a rectangular cavity (100 × 130 [mm]) through the bottom inlet at the constant velocity of u in  = 1 [m/s]. The air flows out through two vents placed in the upper part of the cavity. This system was represented by two-dimensional grid with a size of 256 × 522 and 117,163 active cells belonging to a liquid or a gaseous phase (the rest belongs to the boundary cells). For simplicity, in the simulation, the entire upper wall was treated as the outlet boundary (open to the atmosphere (ρ out  = 1)). On the remaining domain walls the free-slip condition was applied. The free-slip condition was also used on the liquid free surface (w p  = 0 in Eq. (13)). Values of the parameters used in computations are listed in Table 3.

Table 3 Values of parameters used in numerical computations
Full size table

Figure 4 shows the obtained results. During the process gas bubbles are formed between the liquid and cavity walls. They counteract the complete filling of the domain lower part. In case of the piston model the calculation results agree well with the experimental data. Some small deformations visible on the interface line are caused by the high value of flow dimensionless velocity, close to the maximum allowable value in the LBM model - c s . Even in such case the computation algorithm remains stable. Simultaneously in the free-surface model gas bubbles do not occur since type G cells are nearly immediately filled with liquid.

Fig. 4
figure 4

Comparison of the experimental data [37] (left column) and the numerical simulation results obtained by the piston model (center column) and free surface model (right column)

Full size image

It should be mentioned here that this simple test case can constitute problem for the lattice Boltzmann SRT algorithms. For the discussed system of a length of 0.1 [m] in the x direction and the assumed viscosity of liquid and gaseous phases, in order to obtain τ in the stability interval it is necessary - in accordance with Eq. (19) - to apply the lattice which has in this direction from 2141 to 6059 cells (N min = 369 , N max = 6059 for the gaseous phase and N min = 2141 , N max = 35196 for the liquid phase), resulting in long computation time. As can be seen, by means of the presented FS method it was possible to perform a stable and accurate simulation for the lattice of much lower resolution. Additionally, the calculation results for lattices with 256, 128 and 64 cells in the x axis direction are shown in Fig. 5. In the first two cases the results are very similar. Only for the 64 × 132 grid the influence of the increased lattice step on the liquid-gas interface shape can be noticed. In this case gas bubbles between liquid and the domain walls are smaller than the assumed lattice step and therefore are not visible in the simulation results. It is important that in each case the simulation process was characterized by a sufficient stability and the system filling ratio was at a similar level as for experimental results.

Fig. 5
figure 5

Simulation results after 0.24 [s] for different grid resolution: (a) 256 × 522, (b) 128 × 262, (c) 64 × 132

Full size image

7.2 Gas back pressure

The influence of the gas back pressure on the liquid motion was also analyzed. The experiments were performed by means of the experimental system shown in Fig. 6a. It was made up of the liquid container “1” placed at a certain height (to obtain - typical for the foundry engineering - a gravity driven flow) and connected by pipes with the so-called gating column “3”. The task of this element - consisting of a set of sieves and vents - was to stabilize a flow and to eliminate air bubbles from it. When valve “2” is opened water flows from the container via the column to the transparent acrylic mold “4”. The water-air flow in the mold, was observed by the fast (up to 50,000 FPS) digital camera. To achieve the proper synchronization between the computational results and experimental data the triggering device (LED - phototransistor) was applied in the gating column. The camera recorded images after specific time from the trigger signal (moment when colored water covered the phototransistor). In a similar fashion the time after liquid reaches the lattice cell corresponding to the trigger localization in the experimental set-up, was recorded in simulations.

Fig. 6
figure 6

Schematic presentation of the model system (a) and its fragment represented in the numerical simulations (b)

Full size image

In order to enable the flow observations the mold and gating column was made from glued and sealed acrylic glass plates (Fig. 7). The mold was lighted from the back by LEDs which flash was coupled with the trigger signal. The mold with channels forming the rotated letter “Y” in two versions, called the type A and type B (Fig. 7) was used in tests. In the type A the air filling the system was freely pushed out through two outlets (to the atmosphere) by flowing water. In the type B variant the upper outlet was closed. Therefore it was expected that the gas pressure would start to increase significantly, which - in turn - should influence the liquid stream motion. To measure the air pressure changes, the pressure sensor was used.

Fig. 7
figure 7

Photo of acrylic glass mold (left) and the schematic presentation of two variants of the model system used in experiments (center and right), with marked inlets and outlets

Full size image

The obtained experimental results were compared with the data from numerical simulations. Due to a high efficiency of the presented approach it was possible to reflect in computations a larger part of the experimental stand together with the gating column fragment (Fig. 6b). Two dimensional lattice consisting of 591,300 cells (including 186,184 active cells) was used. Again the free-slip boundary condition was applied on domain walls and at the liquid free surface (w p  = 0). The inflow velocity was 0.19 [m/s], while g c  = 3.16e − 5 (Eq. (18)). Values of the remaining parameters used in computations were the same as given in Table 3.

Photos of the flow in the type A system, recorded by the camera after t = 0.4 [s] and t = 0.45 [s] (from the trigger signal), are shown in Fig. 8 together with the visualization (in FieldView 15 software) of the numerical simulation results. As can be seen in both cases the mold pouring process is similar. This concerns the filling level of the system as well as the free surface shape.

Fig. 8
figure 8

Comparison of experimental data (left column) and the numerical simulation results (right column) for the type A system

Full size image

At the initial stage of pouring (t = 0.4 [s]) water flows - under an influence of the gravity force - in the direction of the lower elbow. However the inlet velocity is high enough to make water to start filling the upper elbow too (t = 0.45 [s]). The air is pushed out through two outlets and therefore its pressure (density) in both elbows is similar. This is illustrated in Fig. 9a.

Fig. 9
figure 9

Comparison of density and streamlines in a gaseous phase obtained from the simulations for the type A (a) and B (b) system at t = 0.38 [s]

Full size image

However, in case of the type B system this process looks differently (Fig. 10).

Fig. 10
figure 10

Comparison of the experimental data (left column) and the numerical simulation results (right column) for the type B system

Full size image

The air closed in the upper elbow, already from the very beginning of the process, significantly slows down the water stream motion, even when the pressure/density differences in the various areas of the mold at this stage are relatively small (Fig. 9b). The gas can be pushed out from the system by the lower outlet only. Therefore after t = 0.4 [s] the model liquid reaches only the place where the horizontal inlet channel joins the vertical one. Then at t = 0.45 [s] water starts flowing to the lower elbow. The liquid stream ‘breaks’ characteristically at an angle close to the right one but does not fill the upper elbow since the increased air pressure prevents it. Such casting mold pouring process would lead to misrun formations.

The obtained results indicate that the model properly represents the gas back pressure effect. It is also clear from the direct comparison of pressure curves (Fig. 11) recorded in the control point, where after about 0.45 [s] from the trigger signal (moment at which the upper elbow is completely separated by the flowing liquid) a significant pressure jump is seen.

Fig. 11
figure 11

Pressure changes in a gaseous phase (pressure measurement point) for the type B system

Full size image

8 Conclusions

The obtained results indicate that the presented piston model describes properly interactions between fluids filling the casting mold for flows with the velocity range within the incompressible limits. This model correctly represents such phenomena as a gas bubble formation and gas back pressure effect which are of the essential meaning from the point of view of the casting practice. Simultaneously, the proposed solution allows to simulate local velocity and pressure/density changes in the gaseous phase while maintaining characteristic - for the lattice Boltzmann method - transparency and simplicity (efficiency) of the computational algorithm. Equally important is the fact that the piston model - which is a SRT approach - has a sufficient stability (even for low resolution grids) in case of large viscosity differences of both fluids.

Additionally, for the presented solutions, the demand for the operating memory is significantly smaller than in the typical two-phase models for the LBM. In the piston model there is no need for storing separate sets of variables characterizing the flow of each phase. In the interface cells, which are filled with liquid as well as gas, such parameters as density and velocity are treated as averaged values for both fluids. In consequence, behavior of modeled phases can be described by means of the single set of variables (in the same way as for free-surface flows). Also no additional diffusion-correction steps are required since the phase separation assumption is always maintained. These features cause that the presented here simplified approach to modeling of two-phase flows can be successfully used in simulations of the mold filling process.