1 Introduction

In the uncapacitated facility location (UFL) problem the goal is to open facilities in a subset of given locations and connect each client to an open facility so as to minimize the sum of opening costs and connection costs. In the penalty avoiding (prize collecting) variant of the problem, a fixed penalty can be paid instead of connecting a client.

In the k-level facility location problem (k-level UFL) we have a set C of clients and a set \(F = \bigcup _{l = 1}^{k} F_{l}\) of facilities (locations to potentially open a facility). Facilities are of k different types (levels), e.g., for k = 3 one may think of these facilities as shops, warehouses and factories. Each set F l contains facilities on level l. Each facility i has cost of opening it f i and for each i, j∈C∪F there is distance c i, j ≥ 0 which satisfies the triangle inequality. The task is to connect each client to an open facility at each level, i.e., for each client j it needs to be connected with a path (j, i 1,i 2,⋯ ,i k−1,i k ), where i l is an open facility at level l. We aim at minimizing the total cost of opening facilities (at all levels) plus the total connection cost, i.e., the sum of the lengths of clients paths.

In the k-level uncapacitated facility location problem with penalties (k-level UFLWP), the setting is the same as k-level UFL except that each client j can either be connected to a path, or be rejected in which case the penalty p j must be paid ( p j can be considered as the loss of profit). The goal is to minimize the sum of the total cost of opening facilities (at all levels), the total connection cost and the total penalty cost. In the uniform version of the problem all penalties are the same, i.e., for any two clients j 1,j 2∈C we have \(p_{j_{1}} = p_{j_{2}}\).

1.1 Related Work and Our Contribution

The studied k-level UFL, generalizes the standard 1-level UFL, for which Guha and Khuller [13] showed a 1.463-hardness of approximation. The hardness for multilevel variant was recently improved by Krishnaswamy and Sviridenko [15] who showed 1.539-hardness for two levels ( k = 2) and 1.61-hardness for general k. This demonstrates that multilevel facility location is strictly harder to approximate than the single level variant for which Li [16] presented the current best known 1.488-approximation algorithm by using a non-trivial randomization of a certain scaling parameter in the LP-rounding algorithm by Chudak and Shmoys combined with a primal-dual algorithm of Jain et al.

The first constant factor approximation algorithm for k = 2 is due to Shmoys, Tardos, and Aardal [18], who gave a 3.16-approximation algorithm. For general k, the first constant factor approximation algorithm was the 3-approximation algorithm by Aardal, Chudak, and Shmoys [1].

As it was naturally expected that the problem is easier for smaller number of levels, Ageev, Ye, and Zhang [2] gave an algorithm which reduces an instance of the k-level problem into a pair of instances of the (k−1)-level problem and of the single level problem. By this reduction they obtained 2.43–apx. for k = 2 and 2.85–apx. for k = 3. This was later improved by Zhang [22], who got 1.77–apx for k = 2, 2.53–apx Footnote 1 for k = 3, and 2.81-apx for k = 4. Byrka and Aardal [5] then improved the approximation ratio for k = 3 to 2.492.

1-level UFL with penalties was first introduced by Charikar et al. [9], who gave a 3-approximation algorithm based on a primal-dual method. Later, Jain et al. [14] indicated that their greedy algorithm for UFL could be adapted to UFLWP with the approximation ratio 2. Xu and Xu [20, 21] proposed a 2.736-approximation algorithm based on LP-rounding and a combinatorial 1.853-approximation algorithm by combining local search with primal-dual. Later, Geunes et al. [12] presented an algorithmic framework which can extend any LP-based α-approximation algorithm for UFL to get an (1−e −1/α)−1-approximation algorithm for UFL with penalties. As a result, they gave a 2.056-approximation algorithm for this problem. Recently, Li et al. [17] extended the LP-rounding algorithm by Byrka and Aardal [5] and the analysis by Li [16] to UFLWP to give the currently best 1.5148-approximation algorithm.

For multi-level UFLWP, Bumb [4] gave a 6-approximation algorithm by extending the primal-dual algorithm for multi-level UFL. Asadi et al. [3] presented an LP-rounding based 4-approximation algorithm by converting the LP-based algorithm for UFLWP by Xu and Xu [20] to k-level.

Zhang [22] predicted the existence of an algorithm for k-level UFL that for any fixed k has approximation ratio strictly smaller than 3. In this paper we give such an algorithm, which is a natural generalization of LP-rounding algorithms for 1-level UFL. We further improve the ratios by extending the randomization process proposed by Li [16] for 1-level UFL to k-level UFL. Our new LP-rounding algorithm improves the currently best known approximation ratio for k-level UFL for any k > 2. The ratios we obtain for k≤10 are summarized in the following table.

In addition, we show that our algorithm can be naturally generalized to get an improved approximation algorithm for k-level UFLWP.

1.2 The Main Idea Behind Our Algorithm

The 3-approximation algorithm of Aardal, Chudak, and Shmoys, rounds a fractional solution to the standard path LP-relaxation of the studied problem by clustering clients around so-called cluster centers. Each cluster center gets a direct connection, while all the other clients only get a 3-hop connection via their centers. In the single level UFL problem, Chudak and Shmoys observed that by randomly opening facilities one may obtain an improved algorithm using the fact that for each client, with at least some fixed probability, he gets an open facility within a 1-hop path distance. While in the single level problem independently sampling facilities to open is sufficient, the multilevel variant requires coordinating the process of opening facilities across levels.

The key idea behind our solution relies on an observation that the optimal integral solution has a form of a forest, while the fractional solution to the standard LP-relaxation may not have this structure. We start by modifying the instance and hence the LP, so that we enforce the forest structure also for the fractional solution of the relaxation. Having the hierarchical structure of the trees, we then use the technique of Garg, Konjevod, and Ravi [11], to first round the top of the tree, and then only consider the descendant edges if the parent edge is selected. This approach naturally leads to sampling trees (not opening lower level facilities if their parent facilities are closed), but to eventually apply the technique to a location problem, we need to make it compatible with clustering. To this end we must ensure that all cluster centers get a direct 1-hop path service. This we obtain by a specific modification of the rounding algorithm, which ensures opening exactly one direct path for each cluster center, while preserving the necessary randomness for all the other clients. It is only possible because cluster centers do not share top level facilities, and in rounding a single tree we only care about at most one cluster center. In Section 3.2 we propose a token-passing based rounding procedure which has exactly the desired properties.

The key idea behind importing the randomization process to k-level UFL relies on an observation that algorithms whose performance can be analysed with a linear function of certain instance parameters, like the Chudak and Shmoys algorithm [10] for UFL, can be easily combined and analysed with a natural factor revealing LP. This simplifies the argument of Shi Li [16] for his 1.488-approximation algorithm for UFL as an explicit distribution for the parameters obtained by a linear program is not necessary in our factor revealing LP. With this tool one can easily randomize the scaling factor in LP-rounding algorithms for various variants of the UFL problem.

2 Extended LP Formulation for k-level UFL

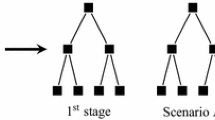
To describe our new LP we first describe a process of splitting vertices of the input graph into a number of (polynomially many for fixed k) copies of each potential facility location.

Graph modification.

Our idea is to have a graph in which each facility t on level j may only be connected to a single facility on level j + 1. Since we do not know a priori to which facility on level j + 1 facility t is connected in the optimal solution, we will introduce multiple copies of t, one for each possible parent on level j + 1.

To be more precise, we let F ′ denote the original set of facilities, and we construct the new set of facilities denoted by F. Nothing will change for facilities in set \(F^{\prime }_{k}\), so \(F_{k} = F^{\prime }_{k}\). For each facility \(t \in F^{\prime }_{k-1}\) we have |F k | facilities each connected with different facility in set F k . So the cardinality of the set F k−1 is equal to \(|F_{k}| \cdot |F^{\prime }_{k-1}|\). In general: for each i = 1, 2, . . . ,k−1 set F i has |F i + 1| copies of each element in set \(F^{\prime }_{i}\) and each copy is connected with a different element in the set F i + 1, so \(|F_{i}| = |F_{i+1}| \cdot |F^{\prime }_{i}|\). Observe that so created copies of facilities at level l are in one to one correspondence with paths (i l ,i l + 1,…,i k ) on original facilities on levels l, l + 1,…,k. We will use such paths on the original facilities as names for the facilities in the extended instance.

The distance between any two copies i 1,i 2 of element i is equal to zero and the cost of opening facility i 1 and i 2 is the same and equal to f i . If \(i_{1}^{\prime }\) is a copy of i 1 and \(i_{2}^{\prime }\) is a copy of i 2 then \(c_{i_{1}^{\prime }i_{2}^{\prime }} = c_{i_{1}i_{2}}\). Distance between copy of facility i and client c is equal to c c i . Set C of clients will stay unchanged (Fig. 1).

Fig. 1
figure 1

Figure presets graph before (left part) and after (right part) modification. As you can see the set of vertices in the highest level does not change

Full size image

Connection and Service Cost.

P C is the set of paths (in the above described graph), which start in some client and end in a facility at level k. P j is the set of facilities at level j in the extended instance, or alternatively the set of paths on original facilities which start in a facility at level j and end in a facility at level k. Now we define the cost of path p denoted by c p . For p = (c, i 1,i 2,⋯i k )∈P C we have \(c_{p} = c_{c, i_{1}} + c_{i_{1}, i_{2}} + \ldots + c_{i_{k-1}, i_{k}}\) and for p = (i j ,i j + 1,⋯i k )∈P j we have \(c_{p} = f_{i_{j}}\). So if p∈P C then c p is a service cost (i.e., the length of path p), and if p∈P j then c p is the cost of opening the first facility on this path. \(P = P_{C} \cup \bigcup _{j = 1}^{k} P_{j}\).

2.1 The LP

$$ min \sum\limits_{p \in P} x_{p}c_{p}$$
(1)
$$ \sum\limits_{p \in P_{C} : j \in p} x_{p} \geq 1 ~~~~~\forall_{j \in C} $$
(2)
$$\begin{array}{@{}rcl@{}} x_{(i_{l+1}, i_{l+2}, {\ldots} i_{k})} -x_{(i_{l}, i_{l+1}, {\ldots} i_{k})} &\geq& 0 ~~~~~\forall_{p = (i_{l}, i_{l+1}, {\ldots} i_{k}) \in P_{l}, l<k} \end{array} $$
(3)
$$x_{q} - \sum\limits_{p = (j, {\ldots} i_{l}, i_{l+1} {\ldots} i_{k}) \in P_{C}} x_{p} \geq 0 ~~~~~\forall_{j \in C} \forall_{q = (i_{l}, i_{l+1}, {\ldots} i_{k}) \in P \setminus P_{C}}$$
(4)
$$ x_{p} \geq 0 ~~~~~\forall_{p \in P} $$
(5)

The natural interpretation of the above LP is as follows. Inequality (1) states that each client is assigned to at least one path. Inequality (2) encodes that opening of a lower level facility implies opening of its unique higher level facility. The most complicated inequality (3) for a client j∈C and a facility i l ∈F l , imposes that the opening of i l must be at least the total usage of it by client j.

Let \(p \sqsupset q\) denote that p is suffix of q. The dual program to the above LP is:

$$\begin{array}{@{}rcl@{}} max \sum\limits_{j \in C} v_{j} \end{array} $$
(6)
$$\begin{array}{@{}rcl@{}} v_{j} - \sum\limits_{q \in P_{1} : q \sqsupset p} y_{p} - \sum\limits_{q \in P \setminus P_{C} : q \sqsupset p} w_{j,q} &\leq& c_{p} ~~~~~\forall_{j} \forall_{p \in P_{C}} \end{array} $$
(7)
$$\begin{array}{@{}rcl@{}} \sum\limits_{q \in P_{k-1} : p \sqsupset q} y_{q} + \sum\limits_{j \in C} w_{j, p} &\leq& c_{p} ~~~~~\forall_{p \in P_{k}} \end{array} $$
(8)
$$\begin{array}{@{}rcl@{}} \sum\limits_{q \in P_{l-1} : p \sqsupset q} y_{p} - \sum\limits_{q \in P_{l+1} : q \sqsupset p} y_{p} + \sum\limits_{j \in C} w_{j, p} &\leq& c_{p} ~~~~~\forall_{l \in \{1, \ldots, k-1\}} \forall_{p \in P_{l}} \end{array} $$
(9)
$$\begin{array}{@{}rcl@{}} v_{j}, y_{p}, w_{j,q} &\geq& 0 ~~~~~~\forall_{j,p,q} \end{array} $$
(10)

Lemma 1

Let x and ( v,y,w) be optimal solutions to the above primal and dual linear programs, respectively. For any p∈P C , if x p >0, then c p ≤v j , where j is the client connected by the path c p .

Proof

Using (7) we can write the following complementary slackness condition:

$$ x_{p}~(c_{p} - v_{j} + \sum\limits_{q \in P_{1} : q \sqsupset p} y_{p} + \sum\limits_{q \in P \setminus P_{C} : q \sqsupset p} w_{j,q}) = 0~\forall_{j \in C}~\forall_{p \in P_{C} : j \in p} $$

We are interested in p for which x p > 0, so

$$ c_{p} + \sum\limits_{q \in P_{1} : q \sqsupset p} y_{p} + \sum\limits_{q \in P \setminus P_{C} : q \sqsupset p} w_{j,q} = v_{j} $$

From (10) we know that each variable in the dual program is non-negative, so we obtain that x p > 0 implies c p ≤v j . □

Let x ∗ be an optimal fractional solution to LP (1)–(5). Let \(P^{j} = \{p \in P_{C} | j \in p \wedge x^{*}_{p} > 0\}\) denote the set of paths beginning in client j, which are in the support of solution x ∗. Define \(d^{av}(j) = C_{j}^{*} = {\sum }_{p \in P^{j}} c_{p} x_{p}^{*}\), \(d^{max}(j) = \max _{p\in P^{j} : x^{*}_{p} > 0} c_{p} \leq v_{j}\), and \(F_{j}^{*} = v^{*}_{j} - C_{j}^{*}\). Naturally, \(F^{*} = {\sum }_{j \in C} F_{j}^{*}\) and \(C^{*} = {\sum }_{j \in C} C_{j}^{*}\).

3 Algorithm and Analysis for k-level UFL

The approximation algorithm A(γ) presented below is parameterized by γ. It has the following major steps:

  1. 1.

    formulate and solve the extended LP (1)–(5);

  2. 2.

    scale up facility opening by γ ≥ 1 (optional, only to improve the approximation ratio)

  3. 3.

    cluster clients;

  4. 4.

    round facility opening (tree by tree);

  5. 5.

    connect each client j with a closest open connection path p∈P j.

It starts by solving the above described extended LP which, by contrast to the LP used in [1], enforces the fractional solution to have a forest like structure. Step 3. can be interpreted as an adaptation of (by now standard) LP-rounding techniques used for (single level) facility location. Step 4. is an almost direct application of a method from [11]. The final connection Step 5. is straightforward, the algorithm simply connects each client via a shortest path of open facilities.

For the clarity of presentation we first only describe the algorithm without scaling which achieves a slightly weaker approximation ratio. We will now present Steps 3. and 4. in more detail.

3.1 Clustering

Like in LP-rounding algorithms for UFL, we will partition clients into disjoint clusters and for each cluster center select a single client which will be called the center of this cluster.

Please recall that the solution x ∗ we obtain by solving LP (1)-(5) gives us (possibly fractional) weights on paths. Paths p∈P C we interpret as connections from clients to open facilities, while other (shorter) paths from P∖P C encode the (fractional) opening of facilities, which have a structure of a forest (i.e., every facility from a lower level is assigned only to a single facility at a higher level).

Observe that if two client paths p 1,p 2∈P C share at least one facility, then they must also end in the same facility at the highest k-th level. For a client j and a k-th level facility i we will say j is fractionally connected to i in x ∗ if and only if there exists a path p∈P C of the form (j,…,i) with x p > 0. Two clients are called neighbors if they are fractionally connected to the same k-th level facility.

The clustering is done as follows. Consider all clients to be initially unclustered. While there remains at least one unclustered client do the following:

  • select an unclustered client j that minimizes d av(j)+d max(j),

  • create a new cluster containing j and all its yet unclustered neighbors,

  • call j the center of the new cluster;

The procedure is known (see e.g., [10]) to provide good clustering, i.e., no two cluster centers are neighbors and the distance from each client to his cluster center is bounded.

3.2 Randomized Facility Opening

We will now give details on how the algorithm decides which facilities to open. Recall that the facility opening part of the fractional solution can be interpreted as a set of trees rooted in top level facilities and having leafs in level-1 facilities.

We will start by describing how a single tree is rounded. For the clarity of presentation we will change the notation and denote the set of vertices (facilities) of such tree by V, and we will use x v to denote the fractional opening of v∈V in the initial fractional solution x ∗. We will also use y v to denote how much a cluster center uses v. Please note, that for each of the trees of the fractional solution there is at most one cluster center client j using this tree. If the tree we are currently rounding is not used by any cluster center, then we set all y v =0. If cluster center j uses the tree, then for each facility v in the tree, we set \(y_{v} = {\sum }_{p \in P^{j} : v \in p} x_{p}\), i.e., y v is the sum over the connection paths p of j crossing v of the extent the fractional solution uses this path.

Let p(v) denote the parent node of v for all (not-root) nodes, and let C(v) denote the set of children nodes of v for all nodes except on the lowest level. Observe, that x and y satisfy:

  1. 1.

    if v is not a leaf, then \(y_{v} = {\sum }_{u \in C(v)} y_{u}\);

  2. 2.

    if v is not the root node, then x v ≤x p(v);

  3. 3.

    for all v∈V we have x v ≥ y v .

figure a

The following randomized procedure will be used to round both the fractional x into an integral \(\hat {x}\) and the fractional y into an integral \(\hat {y}\). The procedure will visit each node of the tree at most once. For certain nodes it will be run in a’ with a token’ mode and for some others it will be run’ without a token’. It will be initiated in the root node and will recursively execute itself on a subset of lower level nodes. Initially \(\hat {x}_{v}\) and \(\hat {y}_{v}\) are set to 0 for all nodes v, and unless indicated otherwise a node does not have a token.

Now we briefly describe what the algorithm does. Suppose that we are in node v which is not a leaf. If v has a token then we set \(\hat {x}_{v} = \hat {y}_{v} = 1\), choose one son (each son i has probability \(\frac {y_{i}}{y_{u}}\)) and give him a token. Make recursive call on each son. If v doesn’t have a token then with probability \(\frac {x_{v} - y_{v}}{x_{pred} - y_{v}}\) ( x p r e d is 1 if v is a root or x p(v) otherwise) set \(\hat {x}_{v}=1\) and make recursive call on each son. If v is a leaf we don’t choose a son to give him the token and don’t make a recursive call on sons. We execute the above procedure on the root of the tree, possibly assigning the token to the root node just before the execution. Observe, that an execution of the procedure ROUND(v) on a root of the tree brings the token to a single leaf of the tree if and only if it starts with the token at the root node. In case of the token, the \(\hat {y}_{v}\) variables will record the path of the token, and hence will form a single path from the root to a leaf.

Consider a procedure that first with probability y r gives the token to the root r of the tree and then executes ROUND(r). We will argue that this procedure preserves marginals when used to round x into \(\hat {x}\) and y into \(\hat {y}\).

Lemma 2

\(E[\hat {y}_{v}] = y_{v}\) for all v∈V.

Proof

By induction on the distance of v from the root r. \(E[\hat {y}_{r}]\) is just the probability that we started with a token in r, hence it is y r . For a non-root node v, by inductive assumption, his parent node u = p(v) has \(E[\hat {y}_{u}] = y_{u}\). The probability of \(\hat {y}_{v}=1\) can be written as:

$$\begin{array}{@{}rcl@{}} Pr[\hat{y}_{v}=1] &=& Pr[\hat{y}_{v}=1 | \hat{y}_{u}=1]\cdot Pr[\hat{y}_{u}=1] + Pr[\hat{y}_{v}=1 | \hat{y}_{u}=0]\cdot Pr[\hat{y}_{u}=0]\\ &=& \frac{y_{v}}{y_{u}}\cdot y_{u} + 0 = y_{v}. \end{array} $$

□

Lemma 3

\(E[\hat {x}_{v}] = x_{v}\) for all v∈V.

Proof

By Lemma 2 is is now sufficient to show, that \(E[\hat {x}_{v} - \hat {y}_{v}] = x_{v} - y_{v}\) for all v∈V. Observe that \(\hat {x}_{v} - \hat {y}_{v}\) is always either 0 or 1, hence \(E[\hat {x}_{v} - \hat {y}_{v}] = Pr[\hat {x}_{v}=1, \hat {y}_{v}=0]\).

The proof is again by induction on the distance of v from the root node r. Clearly, \(E[\hat {x}_{r} - \hat {y}_{r}] = Pr[\hat {x}_{r}=1, \hat {y}_{r}=0] = Pr[\hat {x}_{r}=1 | \hat {y}_{r}=0 ] \cdot Pr[\hat {y_{r}}=0] = \frac {x_{r} - y_{r}}{1 - y_{r}} \cdot (1 - y_{r}) = x_{r} - y_{r}\).

For a non-root node v, by inductive assumption, his parent node u = p(v) has \(E[\hat {x}_{u}] = x_{u}\). Note that \(\hat {y}_{v}=1\) implies \(\hat {x}_{u}=1\). Hence, by Lemma 2, \(Pr[\hat {x}_{u}=1,\hat {y}_{v}=0] = x_{u} - y_{v}\). The probability of \(\hat {x}_{v}=1\) and \(\hat {y}_{v}=0\) can be written as:

$$\begin{array}{@{}rcl@{}} Pr[\hat{x}_{v}=1,\hat{y}_{v}=0] &=& Pr[\hat{x}_{v}=1,\hat{x}_{u}=1, \hat{y}_{v}=0] \\ &=& Pr[\hat{x}_{v}=1 | \hat{x}_{u}=1, \hat{y}_{v}=0] \cdot Pr[\hat{x}_{u}=1,\hat{y}_{v}=0]\\ &=& \frac{x_{v} - y_{v}}{x_{u} - y_{v}} \cdot (x_{u} - y_{v}) = x_{v} - y_{v}. \end{array} $$

□

To round the entire fractional solution we run the above described single tree rounding procedure as follows:

  1. 1.

    For each cluster center j, put a single token on the root node of one of the trees he is using in the fractional solution. Every single tree is selected with probability equal the fractional connection of j to this tree.

  2. 2.

    Execute the ROUND(.) procedure on the root of each tree.

By the construction of the rounding procedure, every single cluster center, since he had placed his token on a tree, will have one of his paths open so that he can directly connect via this path. Moreover, by Lemma 2 the probability of opening a particular connection path p∈P j for him (as indicated by variables \(\hat {y}\)) is exactly equal the weight x p the fractional solution assigns to this path. Hence, his expected connection cost is exactly his fractional cost.

To bound the expected connection cost of the other (non-center) clients is slightly more involved and will be discussed in the following section.

3.3 Analysis

Let us first comment on the running time of the algorithm. The algorithm first solves a linear program of size O(n k), where n is the maximal number of facilities on a single level. For fixed k it is of polynomial size, hence may be directly solved by the ellipsoid algorithm. The rounding of facility openings is by traversing trees whose total size is again bounded by O(n k). Finally each client can try each of his at most O(n k) possible connecting paths and see which of them is the closest open one.

Every client j will find an open connecting path to connect with, since he is a part of a cluster, and the client j ′ who is the center of this cluster certainly has a good open connecting path. Client j may simply use (the facility part of) the path of cluster center j ′, which by the triangle inequality will cost him at most the distance \(c_{j,j^{\prime }}\) more than it costs j ′.

In fact a slightly stronger bound on the expected length of the connection path of j is easy to derive. We use the following bound, which is analogous to the Chudak ans Shmoys [10] argument for UFL.

Lemma 4

For a non central client j∈C, if all paths from P j are closed, then the expected connection cost of client j is

$$E[C_{j}] \leq 2d^{\max}(j) + d^{av}(j). $$

Again like in the work of Chudak ans Shmoys [10], the crux of our improvement lies in the fact that with a certain probability the quite expensive 3-hop path guaranteed by the above lemma will not be necessary, because j will happen to have a shorter direct connection. The main part of the analysis which will now follow is to evaluate the probability of this lucky event.

We will use the following technical lemma.

Lemma 5

For c,d>0, \({\sum }_{i} x_{i} = c\) where ∀ i 1 ≥ x i ≥ 0, we have

$$\prod\limits_{i = 1}^{n} (1 - x_{i} + x_{i}d) \leq \left(1 - \frac{c}{n} + \frac{cd}{n}\right)^{n}. $$

Proof

We will show that \({\prod }_{i = 1}^{n} (1 - x_{i} + x_{i}d) \leq (1 - \frac {c}{n} + \frac {cd}{n})^{n}\) by induction.

Basis: Show that the statement holds for n = 1.

This is trivial as \(x_{1}=\frac {c}{n}\) when n = 1.

Inductive step: Show that if \(\forall _{l < n}, {\prod }_{i = 1}^{l} (1 - x_{i} + x_{i}d) \leq \left (1 - \frac {c}{l} + \frac {c d}{l}\right )^{l}\), then \({\prod }_{i = 1}^{n} (1 - x_{i} + x_{i}d) \leq \left (1 - \frac {c}{n} + \frac {cd}{n}\right )^{n}\).

For each sequence \({\prod }_{i = 1}^{n} (1 - x_{i} + x_{i}d)\), suppose that there exists a subset L⊂X = {x 1,x 2,⋯ ,x n } with l elements (l≤n−1) , and exists x i ∈L with x i ≠c ′/l, where \(c^{\prime } = {\sum }_{x_{i} \in L} x_{i}\). We can replace subsequence \({\prod }_{x_{i} \in L} (1 - x_{i} + x_{i}d)\) with \((1 - \frac {c^{\prime }}{l} + \frac {c^{\prime }d}{l})^{l}\) by our assumption as l<n. The remaining sequence (1−x i +x i d), forall x i ∈X−L will not change. So, the value of the whole sequence will be equal to or bigger than before.

We repeatedly replace the subsequence with the above properties until each element in X is equal to \(\frac {c}{n}\). In the final situation there is no subsequence whose value can be increased. So, the value of the sequence is maximum. Therefore, the inequality \({\prod }_{i = 1}^{n} (1 - x_{i} + x_{i}d) \leq \left (1 - \frac {c}{n} + \frac {cd}{n}\right )^{n}\) holds. □

Suppose a (non-center) client is connected with a flow of value z to a tree in the fractional solution. Suppose further that this flow saturates all the fractional openings on this tree, then the following function f k (z) gives a lower bound on the probability that at least one path of this tree will be open as a result of the rounding routine. Function f k (z) is defined recursively. For k = 1 it is just equal to fractional opening, i.e., f 1(z)=z. For k ≥ 2 it is \(f_{k}(z) = z \cdot \min _{z}(1 - {\prod }_{i = 1}^{n}(1 - f_{k-1}(\frac {z_{i}}{z})))\).Footnote 2 It is a product of the probability of opening the root node, and the (recursively bounded) probability that at least one of the subtrees has an open path, conditioned on the root being open.

The following lemma displays the structure of f k (.).

Lemma 6

Inequality f k (x) ≥ x⋅(1−c) implies f k + 1 (x) ≥ x ⋅ (1−e c−1 ).

Proof

Note that f 1(x) ≥ x and \(f_{2}(x) \geq x (1 - \frac {1}{e})\). Now we show induction step. Suppose that f k (x) ≥ x⋅(1−c) then \(f_{k+1}(x) = x \cdot (1 - \max _{x}{\prod }_{i = 1}^{n}(1 - f_{k}(\frac {x_{i}}{x}))) \geq x \cdot (1 - \max _{x}{\prod }_{i = 1}^{n}(1 - \frac {x_{i}}{x} + \frac {x_{i}}{x} \cdot c)) = x(1 - (1 - \frac {1}{n} + \frac {c}{n})^{n}) \mapsto x (1 - e^{c - 1})\). Last equality follows from Lemma 5 applied to vector \(\overline {x}\) defined as \(\overline {x_{i}} = \frac {x_{i}}{x}\). □

Since a single client j may potentially not fully use the opening (capacity) of the tree he is using, a more direct and accurate estimate of his probability of getting a path is the following function f k (x, z) which depends on both the opening of the root node x and the fractional usage of the tree by j given as z.

$$f_{k}(x,z) = \left\{\begin{array}{ll} x & \text{ when } k = 1, \\ x \cdot \min_{x,z} \left(1 - \left(\prod\limits_{i = 1}^{n}\left(1 - f_{k-1}\left(\frac{x_{i}}{x}, \frac{z_{i}}{x}\right)\right)\right)\right) & \text{ otherwise. } \end{array}\right. $$

Fortunately enough, we may inductively prove the following lemma, which states that the worst case for our analysis is when the tree capacity is saturated by the connectivity flow of a client.

Lemma 7

If 1 ≥ x ≥ z ≥ 0, then f k (x,z) ≥ f k (z).

To prove Lemma 7, we show the following result first.

Lemma 8

Suppose 1 ≥ a>0, 1 ≥ x>0, c>0 and \({\sum }_{i}{x_{i}}=c\) . Then \(\max _{x}{\prod }_{i=1}^{n}(1 - ax_{i}) = {\prod }_{i=1}^{n}(1 - a\frac {c}{n})\) . That is, \({\prod }_{i=1}^{n}(1 - ax_{i})\) reaches its biggest value when \(\forall _{i}, x_{i} = \frac {c}{n}\).

Proof

Basis: For n = 1 we have x i =c, so the equality holds.

Inductive step: Show that if ∀ l<n , \(\max _{x}{\prod }_{i=1}^{l}(1 - ax_{i}) = {\prod }_{i=1}^{l}(1 - a\frac {c^{\prime }}{l})\) where \(c^{\prime }={\sum }_{i=1}^{l}{x_{i}}\), then \(\max _{x}{\prod }_{i=1}^{n}(1 - ax_{i}) = {\prod }_{i=1}^{n}(1 - a\frac {c}{n})\) where \(c={\sum }_{i=1}^{n}{x_{i}}\).

Suppose that \({\prod }_{i=1}^{n}(1 - ax_{i})\) gets its biggest value at (β 1,β 2,⋯ ,β n ). If there exists a subset L⊂{1,2,⋯ ,n} with l elements (l≤n−1) , and exists i∈L with β i ≠c ′/l (where \(c^{\prime } = {\sum }_{i \in L} \beta _{i}\)), then we can replace subsequence \({\prod }_{i \in L} (1 - ax_{i})\) with \((1 - a \frac {c^{\prime }}{l})^{l}\) by our assumption as l<n. The remaining sequence (1−a x i ) forall i∉L will not change. So, the value of the whole sequence remains the same.

We repeatedly replace the subsequence with the above properties until each element x i is equal to \(\frac {c}{n}\). So the statement holds. □

Proof of Lemma 7

At first we recall the definitions of the studied functions

$$f_{k}(x,z) = \left\{\begin{array}{ll} x & when \ \ k = 1 \\ x \cdot \min_{x,z} \left(1 - \left(\prod\limits_{i = 1}^{n}\left(1 - f_{k-1}\left(\frac{x_{i}}{x}, \frac{z_{i}}{x}\right)\right)\right)\right) & otherwise \end{array}\right. $$
$$f_{k}(z) = \left\{\begin{array}{ll} z & when \ \ k = 1 \\ z \cdot \min_{z} \left(1 - \left(\prod\limits_{i = 1}^{n}\left(1 - f_{k-1}\left(\frac{z_{i}}{z}\right)\right)\right)\right) & otherwise \end{array}\right. $$

We will prove the lemma by induction on k. Note that for k = 1 we have f k (x, z)=x ≥ z = f k (z). Our assumption is that inequality holds for each l<k and our thesis is that it holds for k. By the inductive assumption it is sufficient to prove:

$$x \cdot \left(1 - \max\nolimits_{z}\prod\limits_{i = 1}^{n}\left(1 - f_{k-1}\left(\frac{z_{i}}{x}\right)\right)\right) \geq z \cdot \left(1 - \max\nolimits_{z}\prod\limits_{i = 1}^{n}\left(1 - f_{k-1}\left(\frac{z_{i}}{z}\right)\right)\right) $$

Note that for some α∈[0,1] we have z = x⋅α. Using the fact that ∀ k f k (x)=c k x (it is because value of \(\min _{z} 1 - ({\prod }_{i = 1}^{n}(1 - f_{k-1}(\frac {z_{i}}{z})))\) does not depend on the value of z - we use only \(\frac {z_{i}}{z}\) which is the same for each value of z) we can write following inequality

$$\frac{z}{\alpha}\left(1 - \max\nolimits_{z}\prod\limits_{i=1}^{n}\left(1 - \frac{c_{k-1}\alpha z_{i}}{z}\right)\right) \geq z\left(1 - \max\nolimits_{z}\prod\limits_{i=1}^{n}\left(1 - \frac{c_{k-1} z_{i}}{z}\right)\right) $$

Lemma (8) impose that above inequality is equivalent with

$$\frac{1}{\alpha}\left(1 - \left(1 - \frac{c_{k-1}\alpha}{n}\right)^{n}\right) \geq \left(1 - \left(1 - \frac{c_{k-1}}{n}\right)^{n}\right) $$

Note that in the limit with n going to infinity we have

$$g(\alpha) = \frac{1}{\alpha}(1 - e^{-c_{k-1}\alpha}) \geq (1 - e^{-c_{k-1}}) $$

For α = 1 we have equality and for α∈[0,1) we have that g ′(α)≤0. Function g is decreasing with increasing α, so inequality holds. □

Consider now a single client j who is fractionally connected to a number of trees with a total weight of his connection paths equal γ (you may think he sends a total flow of value γ through these trees, from leaves to roots). Now, to bound the probability of at least one of these paths getting opened by the rounding procedure, we introduce function F k (γ) defined as follows. \(F_{k}(\gamma ) = 1 - \max _{\gamma } {\prod }_{i = 1}^{n}(1 - f_{k}(x_{i}))\). This function is one minus the biggest chance that no tree gives route from root to leaf, using the previously defined f k (.) function to express the success probability on a single tree.

Now we can give an analogue of Lemma 6 but for F k (γ).

Lemma 9

Inequality F k (γ) ≥ 1−e (c−1)γ implies \(F_{k+1}(\gamma ) \geq 1 - e^{(e^{c-1} - 1)\gamma }\).

Proof

Suppose that f k (x) ≥ x(1−c). Note that \(F_{k}(\gamma ) = 1 - \max _{\gamma } {\prod }_{i = 1}^{n}(1 - f_{k}(x_{i})) \geq 1 - \max _{\gamma } {\prod }_{i = 1}^{n}(1 - x_{i} + x_{i}c)) = 1 - (1 - \frac {\gamma }{n} + \frac {\gamma }{n}c)^{n} \mapsto 1 - e^{(c-1)\gamma }\). (Last equality base on Lemma 5). Key observation is that in the last equality there is no constraint on the positive constant c - we can replace it with any other positive constant and the equality will still be true. Using Lemma 6 we know that f k + 1(x) ≥ x(1−e c−1). The only difference in the way we evaluate F k + 1(γ) is the replacement of constant c by other constant e c−1, so the equality for F k (γ) implies the equality for F k + 1(γ), and hence the lemma holds. □

We are now ready to combine our arguments into a bound on the expected total cost of the algorithm.

Theorem 1

Expected total cost of the algorithm is at most (3−2F k (1))OPT.

Proof

Note first that by Lemma 3, the probability of opening of each single facility equals its fractional opening, and hence the expected facility opening cost is exactly the fractional opening cost F ∗.

Consider client j∈C which is a cluster center. He randomly chooses one of the paths from set P j. Expected connection cost for client j is \(E[C_{j}] = d^{av}(j) = {\sum }_{p \in P^{j}} c_{p}x_{p} = C_{j}^{*}\). Suppose now j∈C is not a cluster center. As discussed above, the chance that at least one path from P j is open is not less than F k (1). Suppose that at least one path from P j is open. Each path from this set has proportional probability to become open, so the expected length of the chosen path is equal to d av(j). If there is no open path in set P j, client j will use a path \(p^{\prime } \in P^{j^{\prime }}\) which was chosen by his cluster center j ′∈C, but j has to pay extra for the distance to the center j ′. In this case, by Lemma 4 we have E[C j ] ≤ 2d max(j)+d av(j).

The total cost of the algorithm can be bounded by the following expression:

$$ F^{*} + \sum\limits_{j \in D} (F_{k}(1)C_{j}^{*} + (1 - F_{k}(1))(2d^{\max}(j) + d^{av}(j))) \leq $$
$$ F^{*} + \sum\limits_{j \in D} (F_{k}(1)C_{j}^{*} + (1 - F_{k}(1))(2(C_{j}^{*} + F_{j}^{*}) + C_{j}^{*})) = $$
$$ (3 - 2F_{k}(1))(F^{*} + C^{*}) $$

Note that F k (1)>0 for each k, so expected total cost of algorithm is strictly less than three times the optimum cost. □

4 How to Apply Scaling – General Idea

By means of scaling up facility opening variables before rounding, just like in the case of 1-level UFL, we gain on the connectivity cost in two ways. First of all, the probability for j of connecting to one of his fractional facilities via a shorter 1-hop path increases, decreasing the usage of the longer backup paths. The second effect is that, in the process of clustering, clients may ignore the furthest of their fractionally used facilities. It has the effect of filtering the solution and reducing the lengths of the 3-hop connections. In fact, if the scaling factor is sufficient, which is the case for our application, we eventually do not need the dual program to upper bound the length of a fractional connection with a dual variable. All this is well studied for UFL (see, e.g., [8]), but would require a few pages to present in full detail.

All we need in order to use the techniques from UFL is to give bounds on the probability of opening a connection to specific groups of facilities as a function of the scaling parameter γ. So the probability of connecting j to one of his close facilities (total opening equal 1 after scaling) will be at least F k (1). The probability of connecting j to either a close or a distant facility (total opening equal γ after scaling) will be at least F k (γ). The probability of using the backup 3-hop path via the cluster center will be at most 1−F k (γ). To obtain the approximation ratios claimed in the table in Section 1.1, it remains to plug in these numbers to the analysis in [8], and for each value of k find the optimal value for the scaling parameter γ. A complete description of the algorithm for k-level UFL using randomized scaling will be given in Section 1.1. Before we dive into the full detail picture, we first discuss the simpler case of UFL in the following Section.

5 Randomized Scaling for UFL - an Overview

Consider the following standard LP relaxation of UFL.

$$\min \sum\limits_{i \in F}{\sum\limits_{j \in C} {c_{ij}x_{ij}}} + \sum\limits_{i \in F} y_{i} f_{i}$$
(11)
$$ \sum\limits_{i \in F} x_{ij}= 1 ~~~~~\forall_{j \in C}$$
(12)
$$ y_{i} - x_{ij}\geq 0 ~~~~~\forall_{i \in F, j \in C}$$
(13)
$$x_{ij}, y_{i} \geq 0 ~~~~~\forall_{i \in F, j \in C} $$
(14)

Chudak and Shmoys [10] gave a randomized rounding algorithm for UFL based on this relaxation. Later Byrka and Aardal [5] considered a variant of this algorithm where the facility opening variables were initially scaled up by a factor of γ. They showed that for γ ≥ γ 0≈1.67 the algorithm returns a solution with cost at most γ times the fractional facility opening cost plus 1+2e −γ times the fractional connection cost. This algorithm, when combined with the (1.11, 1.78)-approximation algorithm of Jain, Mahdian and Saberi [14] (JMS algorithm for short), is easily a 1.5-approximation algorithm for UFL. More recently, Li [16] showed that by randomly choosing the scaling parameter γ from an certain probability distribution one obtains an improved 1.488-approximation algorithm. A natural question is what improvement this technique gives in the k-level variant.

In what follows we present our simple interpretation and sketch the analysis of the randomization by Li. We argue that a certain factor revealing LP provides a valid upper bound on the obtained approximation ratio. The appropriate probability distribution for the scaling parameter (engineered and discussed in detail in [16]) may in fact be directly read from the dual of our LP. While we do not claim to get any deeper understanding of the randomization process itself, the simpler formalism we propose is important for us to apply randomization to a more complicated algorithm for k-level UFL, which we describe next.

5.1 Notation

Let \(\mathcal {F}_{j}\) denote the set of facilities with which client j∈C is fractionally connected, i.e., facilities i with \(x^{*}_{ij} > 0\) in the optimal LP solution (x ∗,y ∗). Since for uncapacitated facility location problems one can split facilities before rounding, to simplify the presentation, we will assume that \(\mathcal {F}_{j}\) contains lots of facilities with very small fractional opening \(y^{*}_{i}\). This will enable splitting \(\mathcal {F}_{j}\) into subsets of desired total fractional opening.

Definition 1 (definition 15 from [16])

Given an UFL instance and its optimal fractional solution (x ∗,y ∗), the characteristic function h j :[0,1]↦R of a client j∈C is the following. Let i 1,i 2,⋯ ,i m denote the facilities in \(\mathcal {F}_{j}\), in a non-decreasing order of distances to j. Then h j (p)=d(i t ,j), where t is the minimum number such that \({\sum }_{s=1}^{t}y^{*}_{i_{s}} \geq p\). Furthermore, define \(h(p) = {\sum }_{j \in C} h_{j}(p)\) as the characteristic function for the entire fractional solution.

Definition 2

Volume of a set F ′⊆F, denoted by v o l(F ′) is the sum of facility openings in this set, i.e., \(vol(F^{\prime }) = {\sum }_{i \in F^{\prime }} y^{*}_{i}\).

For l = 1, 2, . . . , n − 1 define \(\gamma _{l} = 1 + 2 \cdot \frac {n - l}{n}\), which will form the support for the probability distribution of the scaling parameter γ. Suppose that all facilities are sorted in an order of non-decreasing distances from a client j∈C. Scale up all y ∗ variables by γ l and divide the set of facilities \(\mathcal {F}_{j}\) into two disjoint subsets: the close facilities of client \(j, \mathcal {F}_{j}^{C_{l}}\), such that \(vol(\mathcal {F}_{j}^{C_{l}}) = 1\); and the distant facilities \(\mathcal {F}_{j}^{D_{l}} = \mathcal {F}_{j} \setminus \mathcal {F}_{j}^{C_{l}}\). Note that \(vol(\mathcal {F}_{j}^{D_{l}}) = \gamma _{l} - 1\). Observe that\(\frac {1}{\gamma _{k}} < \frac {1}{\gamma _{l}} \Rightarrow \mathcal {F}_{j}^{C_{k}} \subset \mathcal {F}_{j}^{C_{l}}\) and \(\mathcal {F}_{j}^{C_{l}} \setminus \mathcal {F}_{j}^{C_{k}} \neq \emptyset \). We now split \(\mathcal {F}_{j}\) into disjoint subsets \(\mathcal {F}_{j}^{l}\). Define \(\mathcal {F}_{j}^{C_{0}} = \emptyset \) and \(\mathcal {F}_{j}^{l} = \mathcal {F}_{j}^{C_{l}} \setminus \mathcal {F}_{j}^{C_{l-1}}\), where l = 1,2…,n. The average distance from j to facilities in \(\mathcal {F}_{j}^{l}\) is \(c_{l}(j) = {\int }_{1/\gamma _{l-1}}^{1/\gamma _{l}} h_{j}(p)~dp\) for l > 1 and \({\int }_{0}^{1/\gamma _{1}} h_{j}(p)~dp\) for l = 1. Note that c l (j)≤c l + 1(j) and \(D_{\max }^{l}(j) \leq c_{l+1}(j)\), where \(D_{\max }^{l}(j) = \max _{i \in \mathcal {F}_{j}^{l}}{c_{ij}}\).

Since the studied algorithm with the scaling parameter γ = γ k opens each facility i with probability \(\gamma _{k} \cdot y_{i}^{*}\), and there is no positive correlation between facility opening in different locations, the probability that at least one facility is open from the set \(\mathcal {F}_{j}^{l}\) is at least \(1 - e^{-\gamma _{k} \cdot vol(\mathcal {F}_{j}^{l})}\).

Crucial to the analysis is the length of a connection via the cluster center j ′ for client j when no facility in \(\mathcal {F}_{j}\) is open. Consider the algorithm with a fixed scaling factor γ = γ k , an arbitrary client j and its cluster center j ′. Li gave the following upper bound on the expected distance from j to an open facility around its cluster center j ′.

Lemma 10 (Lemma 14 from [16])

If no facility in \(\mathcal {F}_{j}\) is opened, the expected distance to the open facility around j ′ is at most \(\gamma _{k} D_{av}(j) + (3 - \gamma _{k})D_{\max }^{k}(j)\) , where \( D_{av}(j) = {\sum }_{i \in \mathcal {F}_{j}} c_{ij}x_{ij}^{*}\).

Corollary 1

If γ=γ k , then the expected connection cost of client j is at most

$$ E[C_{j}] \leq \sum\limits_{l = 1}^{n} c_{l}(j) \cdot p_{l} + e^{-\gamma_{k}} \cdot (\gamma_{k} D_{av}(j) + (3 - \gamma_{k})D_{\max}^{k} (j)) $$

where p l is the probability of the following event: no facility is opened in distance at most \(D_{\max }^{l-1}(j)\) and at least one facility is opened in \(\mathcal {F}_{j}^{l}\).

Corollary 2

If γ=γ k , then the expected connection cost of client j is at most

$$\begin{array}{@{}rcl@{}} E[C_{j}] \leq c_{1}(j)\left(1-e^{-\frac{\gamma_{k}}{\gamma_{1}}}\right)&+&\sum\limits_{l = 2}^{n} c_{l}(j) \cdot \left(e^{-\frac{\gamma_{k}}{\gamma_{l-1}}} - e^{-\frac{\gamma_{k}}{\gamma_{l}}}\right)\\ &+& e^{-\gamma_{k}} \cdot (\gamma_{k} D_{av}(j) + (3 - \gamma_{k})D_{\max}^{k} (j)). \end{array} $$

Proof

p l is the probability of the following event: no facility is opened within distance at most \(D_{\max }^{l-1}(j)\) and at least one facility is opened in \(\mathcal {F}_{j}^{l}\). We will show that we can get an upper bound for E[C j ] with setting \(p_{1} = 1 - e^{-\frac {\gamma _{k}}{\gamma _{1}}}\) and \(p_{l}= e^{-\frac {\gamma _{k}}{\gamma _{l-1}}} - e^{-\frac {\gamma _{k}}{\gamma _{l}}}\) for all l > 1.

The probability of the following event (denoted by E l ) is at least \(1-e^{-\frac {\gamma _{k}}{\gamma _{l}}}\): at least one facility is opened in distance at most \(D_{\max }^{l}(j)\) [10]. Similarly, the probability of the following event is at least \(1-e^{-\frac {\gamma _{k}}{\gamma _{l-1}}}\): at least one facility is opened in distance at most \(D_{\max }^{l-1}(j)\).

Recall that we have c l (j)≤c l + 1(j) and \(c_{n}(j)\leq \gamma _{k} D_{av}(j) + (3 - \gamma _{k})D_{\max }^{k} (j)\) (otherwise, we never use this 3-hop).

To get \(\max _{p} \{{\sum }_{l = 1}^{n} c_{l}(j) \cdot p_{l} + e^{-\gamma _{k}} \cdot (\gamma _{k} D_{av}(j) + (3 - \gamma _{k})D_{\max }^{k} (j))\}\), we want to make the probability of using 3-hop biggest first. Then, we set the probability of event E n as \(1-e^{-\frac {\gamma _{k}}{\gamma _{n}}}=1-e^{\gamma _{k}}\), which means the probability of using 3-hop is biggest. Next step, we make p n biggest by setting the probability of event E n−1 as \(1-e^{-\frac {\gamma _{k}}{\gamma _{n-1}}}\). So, we have \(p_{n}=1-e^{-\frac {\gamma _{k}}{\gamma _{n}}}-(1-e^{-\frac {\gamma _{k}}{\gamma _{n-1}}})=e^{-\frac {\gamma _{k}}{\gamma _{n-1}}} - e^{-\frac {\gamma _{k}}{\gamma _{n}}}\). By induction, we get that the worst case is as follows: \(p_{l} = e^{-\frac {\gamma _{k}}{\gamma _{l-1}}} - e^{-\frac {\gamma _{k}}{\gamma _{l}}}\) for all l > 1 and \(p_{1}= 1 - e^{-\frac {\gamma _{k}}{\gamma _{1}}}\) . □

5.2 Factor Revealing LP

Consider running once the JMS algorithm and the Chudak and Shmoys algorithm multiple times, one for each choice of the value for the scaling parameter \(\gamma = \gamma _{l} = 1 + 2 \cdot \frac {n - l}{n}, l=1, 2, {\dots }, n-1\). Observe that the following LP captures the expected approximation factor of the best among the obtained solutions, where \({p_{1}^{i}} = 1 - e^{-\frac {\gamma _{i}}{\gamma _{1}}}\) and \({p_{l}^{i}} = e^{-\frac {\gamma _{i}}{\gamma _{l-1}}} - e^{-\frac {\gamma _{i}}{\gamma _{l}}}\) for all l > 1. The objective of the following LP is to construct the worst case configuration of distances c l .

$$\max~T $$
(15)
$$\gamma_{i} f + \sum\limits_{l = 1}^{n} c_{l} \cdot {p_{l}^{i}} + e^{-\gamma_{i}} (\gamma_{i} c + (3 - \gamma_{i})c_{i+1}) \geq T ~\forall_{i < n}$$
(16)
$$\begin{array}{@{}rcl@{}} 1.11 f + 1.78 c &\geq& T \end{array} $$
(17)
$$\begin{array}{@{}rcl@{}} \frac{1}{\gamma_{1}} \cdot c_{1} + \sum\limits_{i = 2}^{n}(\frac{1}{\gamma_{i}} - \frac{1}{\gamma_{i-1}}) \cdot c_{i} &=& c \end{array} $$
(18)
$$\begin{array}{@{}rcl@{}} 0 \leq c_{i} \leq c_{i+1} &\leq& 1~\forall_{i < n} \end{array} $$
(19)
$$f + c = 1$$
(20)
$$ f, c \geq 0 $$
(21)

The variables of this program encode certain measurements of the function h(p) defined for an optimal fractional solution. Intuitively, these are average distances between a client and a group of facilities, summed up for all the clients. The program models the freedom of the adversary in selecting cost profile h(p) to maximize the cost of the best of the considered algorithms. Variables f and c model the facility opening and client connection cost in the fractional solution. Inequality (16) correspond to LP-rounding algorithms with different choices of the scaling parameter γ. Note that D a v (j)=c and \(D_{max}^{i}(j) \leq c_{i+1}\) hold for each client. This fact, together with Corollary 1, justifies inequality (16). Inequality (17) corresponds to the JMS algorithm [14], and equality (18) encodes the total connection cost (Fig. 2).

Fig. 2
figure 2

Worst case profiles of h(p)(i.e., distances to facilities) for k = 1 obtained from solution of the LP in Section 5.2. X-axis is the volume of a considered set and y-axis represents distance to the farthest facility in this set. Values of function h(p) are in one-to-one correspondence with values of c i in LP from Section 5.2

Full size image

Interestingly, the choice of the best algorithm here is not better in expectation than a certain random choice between the algorithms. To see this, consider the dual of the above LP. In the dual, the variables corresponding to the primal constraints (16) and (17) simply encode the probability of choosing a particular algorithm. Our computational experiments with the above LP confirmed the correctness of the analysis of Li [16]. Additionally, from the primal program with distances we obtained the worst case profile h(p) for the state of the art collection of algorithms considered (see Figs. 3, 4 and 5 respectively for a plot of this tight profile and the distributions of the scaling factor for k-level UFL on different number of levels).

Fig. 3
figure 3

Worst case profiles of h(p) (i.e., distances to facilities) for k = 1, 2, 3, 4 obtained from solution of the LP in Section 6 (without JMS algorithm). X-axis is the volume of a considered set and y-axis represents the distance to the farthest facility in that set. Values of function h(p) are in one-to-one correspondence with values of c i in LP from Section 6

Full size image
Fig. 4
figure 4

Probabilities of using a particular γ in a randomized alg. (from the dual LP) for k = 1, 2, 3, 4

Full size image
Fig. 5
figure 5

Probabilities of using a particular γ in a randomized alg. (from the dual LP) for k = 1,2,3,4. Close-up on small probabilities

Full size image

6 Randomized Scaling for k-level UFL

To obtain an improved approximation ratio we run algorithm A(γ) for several values of γ and select the cheapest solution. The factor revealing LP in Section 5.2 gives an upper bound on the approximation ratio. Since the number of levels has influence on connection probabilities, the values of \({p_{l}^{i}}\) need to be defined more carefully than for UFL. In particular, for l = 1 we now have \({p_{1}^{i}} =F_{k}(\frac{\gamma_{i}}{\gamma_{1}})\) and \({p_{l}^{i}} =F_{k}(\frac{\gamma_{i}}{\gamma_{l}}) - F_{k}(\frac{\gamma_{i}}{\gamma_{l-1}}) \) for l > 1.

The Table 1 summarizes the obtained ratios for a single algorithm (run with the best choice of γ for particular k) and for a group of algorithms.

Table 1 Comparison of ratios
Full size table

7 k-Level UFL with Penalties

We now consider the variant of the problem where the planner may decide to pay a penalty (per client) instead of connecting a certain group of clients. First we give a simple argument that the problem with uniform penalties (the penalty for not connecting j is the same for all j∈C) reduces to the problem without penalties. Next we give an algorithm for the general penalty case and show that our bound on the connection plus penalty cost of a client only gets better if the algorithm decides to pay the penalty, effectively showing that the same approximation as for the non-penalty case is possible.

7.1 k-level UFL with Uniform Penalties reduced to k-level UFL

The difficulty of k-level UFLWP lies in the extra choice of each client, that is, the penalty. We will explain how to overcome the penalties by converting the instance of k-level UFLWP to an appropriate instance of k-level UFL. We first consider the easy case of uniform penalties.

Lemma 11

There is an approximation preserving reduction from k-level UFL with uniform penalties to k-level UFL.

Proof

We can encode the penalty of client j∈C as a group of collocated facilities (one from each level) at distance p j to client j, and with opening cost zero. The distance from client j to the penalty-facilities of client j ′ is equal to \(c_{j, j^{\prime }} + p_{j^{\prime }}\). Note that \(p_{j^{\prime }} = p_{j}\). We can run any approximation algorithm for k-level UFL on the modified instance. If in the obtained solution client j is connected with a penalty-facility of client j ′, we can switch j to its penalty-facility without increasing the cost of the solution. We obtain a solution where clients either connect to normal facilities or to their dedicated penalty-facilities. The latter event we interpret (in the solution to the original instance) as a situation where the client pays penalty. □

Lemma 11 implies that for k-level uncapacitated facility location with uniform penalties we have the following approximation ratios. Algorithms for k = 1 and 2 are described in [16] and [22], for k > 2 are described in this article.

k

1

2

3

4

5

6

7

8

9

10

ratio

1.488

1.77

1.97

2.09

2.19

2.27

2.33

2.39

2.43

2.47

Note that the reduction above does not work for the non-uniform case, because then the distance from client j to the penalty-facility of client j ′ could be smaller than p j . Nevertheless we will show that LP-rounding algorithms in this paper can be easily extended to the non-uniform penalty variant.

7.2 Algorithm for k-level UFLWP (nonuniform penalties)

We use the same notations in Section 2 to model k-level UFLWP.

$$\begin{array}{@{}rcl@{}} \min \sum\limits_{p \in P} x_{p}c_{p} &+& \sum\limits_{j \in C} g_{j} p_{j} \end{array} $$
(22)
$$\begin{array}{@{}rcl@{}} \sum\limits_{p \in P_{C} : j \in p} x_{p} + g_{j}&\geq& 1 ~~~~~\forall_{j \in C} \end{array} $$
(23)
$$\begin{array}{@{}rcl@{}} x_{(i_{t+1}, i_{t+2}, {\ldots} i_{k})} -x_{(i_{t}, i_{t+1}, {\ldots} i_{k})} &\geq& 0 ~~~~~\forall_{p = (i_{t}, i_{t+1}, {\ldots} i_{k}) \in P_{t}, t<k} \end{array} $$
(24)
$$\begin{array}{@{}rcl@{}} x_{q} - \sum\limits_{p = (j, {\ldots} i_{t}, i_{t+1} {\ldots} i_{k}) \in P_{C}} x_{p} &\geq& 0 ~~~~~\forall_{j \in C}, \forall_{q = (i_{t}, i_{t+1}, {\ldots} i_{k}) \in P \setminus P_{C}} \end{array} $$
(25)
$$\begin{array}{@{}rcl@{}} x_{p} &\geq& 0 ~~~~~\forall_{p \in P} \end{array} $$
(26)
$$\begin{array}{@{}rcl@{}} g_{j} &\geq& 0 ~~~~~\forall_{j \in C} \end{array} $$
(27)

Inequality (23) states that each client is assigned to at least one path or is rejected. Let (x ∗,g ∗) be an optimal solution to the above LP. Consider the following LP-rounding algorithm A2 parameterized by γ l .

  1. 1.

    formulate and solve the extended LP (22)–(27) to get an optimal solution (x ∗,g ∗);

  2. 2.

    scale up facility opening and client rejecting variables by γ l , then recompute values of \(x^{*}_{p}\) for p∈P C to obtain a minimum cost solution \((\bar {x}, \bar {g});\)

  3. 3.

    divide clients into two groups \(C_{\gamma _{l}} = \{ j \in C | \gamma _{l} \cdot (1 - g_{j}^{*}) \geq 1 \}\) and \(\bar {C}_{\gamma _{l}} = C \setminus C_{\gamma _{l}};\)

  4. 4.

    cluster clients in \(C_{\gamma _{l}}\);

  5. 5.

    round facility opening (tree by tree);

  6. 6.

    connect each client j with a closest open connection path unless rejecting it is a cheaper option.

Our final algorithm is as follows: run algorithm A(γ l ) for each l = 1,2…,n−1 and select a solution with the smallest cost.

Clustering is based on rules described in [10] and is described in Section 3.1. Rounding on a tree is described in Section 3.2. From now on we are considering only scaled up instance \((\bar {x}, \bar {g})\).

7.3 Analysis

The high level idea is that we can consider the instance of k-level UFLWP as a corresponding instance of k-level UFL by showing that the worst case approximation ratio is for clients in set C γ and we can treat the penalty of client j∈C γ as a “penalty-facility” in our analysis. That is, we can overcome penalties by solving an equivalent k-level UFL without penalties. Then, for k-level UFLWP, we can get the same ratios as for k-level UFL, shown in Table 1.

Complete Solution and “one-level” Description.

It is standard in uncapacitated location problems to split facilities to obtain a so called complete solution, where no facility is used less than it is open by a client (see [19] for details). For our algorithm, to keep the forest structure of the fractional solution, we must slice the whole trees instead of splitting individual facilities to obtain the following.

Lemma 12

Each solution of our linear program for k-level UFLWP can be transformed to an equivalent complete solution.

Proof

We should give two copies T ′ and T ′′ of tree T (instead of it) if there is some client j∈C with a positive flow x j p to one of the paths p in the tree T which is smaller than the path opening x p . Let the opening of such“problematic” path be equal to flow x j p in tree T ′. In tree T ′′ it has value equal to the opening in T decreased by x j p . In general each facility in tree T ′(T ′′) has the same opening as in T times \(\frac {x_{jp}}{x_{p}}\left (\frac {x_{p} - x_{jp}}{x_{p}}\right )\). Note that the value of flow from client j (and other clients which are connected with both trees now) should be the same as before adding trees T ′ and T ′′ instead of T. All clients “recompute” their connection values. We sort all paths in increasing connection cost for client j and connect with them (in that order) as strong as it is possible until client j has flow equal to one or it is cheaper to pay penalty instead of connecting with any open path. The important fact is that the expected connection and penalty cost of each client remain the same after above operations.

In the process of coping and replacing trees we add at most |C| new trees. Because each client has at most one “problematic” (not saturating) path. □

For the clarity of the following analysis we will use a “one-level” description of the instance and fractional solution despite its k-level structure. Because the number of levels will have influence only on the probabilities of opening particular paths in our algorithm.

Consider set S j of paths which start in client j and end in the root of a single tree T. Instead of thinking about all paths from set S j separately we can now treat them as one path p T whose fractional opening is \(x_{p_{T}} = {\sum }_{p \in S_{j}} \bar {x}_{p}\) and (expected) cost is \(c_{p_{T}} = \frac {{\sum }_{p \in S_{j}} c_{p} \bar {x}_{p}}{x_{p_{T}}}\). Observe that our distance function \(c_{p_{T}}\) satisfy the triangle inequality. From now on we will think only about clients and facilities (on level k) and (unique) paths between them. Accordingly, we will now encode the fractional solution as \((\bar {x}, \bar {y}, \bar {g})\), to denote the fractional connectivity, opening and penalty components.

Penalty discussion

Lemma 13 The worst case approximation ratio is for clients from set C γ .

Proof

For the clarity of description, we sort facilities i 1,i 2,… in non-decreasing distances from client j. Let m be the number of facilities with positive flow from client j in scaled up solution \((\bar {x}, \bar {y}, \bar {g})\). We have two sets of clients C γ and \(\bar {C}_{\gamma }\). For the first case j∈C γ , we can upper bound its expected connection and penalty cost as follows

$$\begin{array}{@{}rcl@{}} &&{}E[C_{j} + P_{j}] \leq \sum\limits_{r = 1}^{m}\left(F_{k}\left(\sum\limits_{i = 1}^{r} \bar{y}_{i}\right) - F_{k}\left(\sum\limits_{i = 1}^{r-1} \bar{y}_{i}\right)\right) c_{j, i_{r}}\\ &&+ \left(1-F_{k}\left(\gamma \left(1 - g_{j}^{*}\right)\right)\right)\left(\gamma g_{j}^{*} p_{j} + \left(\max \{0, 1 - \gamma g_{j}^{*}\}\right)\right.\\&&{\kern2pc}\left. \times\left(\gamma \left(1 - g_{j}^{*}\right) D_{av}(j) + \left(3 - \gamma \left(1 - g_{j}^{*}\right)\right) D_{\max}^{C}(j)\right)\right)\\ &&{}\leq \sum\limits_{r = 1}^{m}\left(F_{k}\left(\sum\limits_{i = 1}^{r} \bar{y}_{i}\right) - F_{k}\left(\sum\limits_{i = 1}^{r-1} \bar{y}_{i}\right)\right) c_{j, i_{r}} \\&& + \left(1-F_{k}\left(\gamma \left(1 - g_{j}^{*}\right)\right)\right) \max \{1, \gamma g_{j}^{*}\}\\&&{\kern2pc}\times\left(\gamma \left(1 - g_{j}^{*}\right) D_{av}(j) + \left(3 - \gamma \left(1 - g_{j}^{*}\right)\right) D_{\max}^{C}(j)\right). \end{array} $$

The first inequality upper bounds E[C j +P j ] in a similar way as Corollary 1, but in situation when no facility is open in F j we need to consider rejecting j or connection with open facility via cluster center. The second inequality holds because \(p_{j} \leq \gamma \left (1 - g_{j}^{*}\right ) D_{av}(j) + \left (3 - \gamma \left (1 - g_{j}^{*}\right )\right ) D_{\max }^{C}(j)\). Otherwise, j could connect with facility in that distance instead of using penalty.

For the second case we have that \(j \in \bar {C}_{\gamma }\). The expected connection and penalty cost of client j can be upper bounded as follows

$$ E[C_{j} + P_{j}] \leq \sum\limits_{r = 1}^{m}\left(F_{k}\left(\sum\limits_{i = 1}^{r} \bar{y}_{i}\right) - F_{k}\left(\sum\limits_{i = 1}^{r-1} \bar{y}_{i}\right)\right) c_{j,i_{r}} + \left(1-F_{k}\left(\gamma \left(1 - g_{j}^{*}\right)\right)\right) p_{j}, $$

since in situation when no facility is open in F j we only need to consider rejecting j.

Note that each client \(j \in \bar {C_{\gamma }}\) can treat its penalty as a close (and distant) facility, so we can say that \(p_{j} = D_{\max }^{C}(j) = D_{av}^{D}(j)\). Moreover, \(D_{\max }^{C}(j) \leq \gamma \left (1-g_{j}^{*}\right ) D_{av}(j) + \left (3 - \gamma \left (1 - g_{j}^{*}\right )\right ) D_{\max }^{C}(j)\) as \(0<\gamma \left (1 - g_{j}^{*}\right )<1\) according to the definition of \(\bar {C}_{\gamma }\).

Therefore, we have that the worst case approximation ratio is for clients from set C γ . □

Lemma 14

For clients j∈C γ we can treat its penalty as a facility.

Proof

If j is a cluster center, j will have at least one (real) facility open in its set of close facilities. Thus, its connection and penalty cost are independent of the value of \(g_{j}^{*}\). If j is not a cluster center and we pretend its penalty as a facility, no other client j ′ will consider to use this fake facility. Because j ′ only looks at facilities fractionally serving him, and the facilities which serve the center of the cluster containing j ′. □